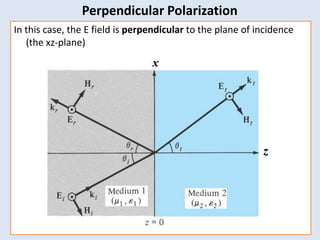
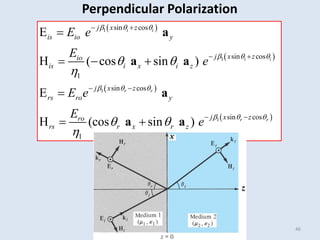
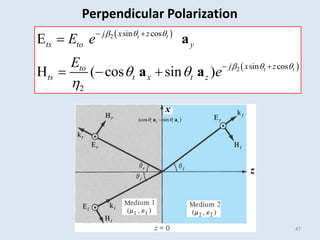
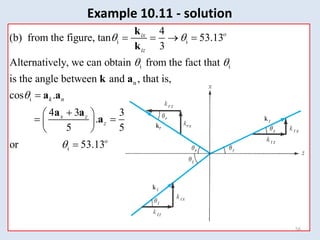
The document discusses electromagnetic wave propagation, focusing on energy transport via EM waves and the mathematical principles governing this, particularly through Maxwell's equations. It introduces the concept of the Poynting vector to describe power flow and details phenomena such as plane wave reflection at material boundaries, including reflection and transmission coefficients. The text provides examples to illustrate these concepts in different media.

1. EELE 3332 – Electromagnetic II
Chapter 10
Electromagnetic Wave
Propagation
Islamic University of Gaza
Electrical Engineering Department
Dr. Talal Skaik
2012 1

2. Energy can be transported from one point (where a transmitter is located)
to another point (with a receiver) by means of EM waves.
The rate of energy transportation can be obtined from
Maxwell's


 
     
     
   
2
2
2
equations:
E
Using Maxwell equation: H E
Dotting both sides with E:
E
E H E
But from vector identities: H E E H H E
E H H E H E
1
H E H E ... (1)
2
t
E
t
E
E
t
 
 
 

  


    

       
       

       

2
10.7 Power and the Poynting Vector

3. 3
 
   
 
 
2
2
2
2 2
2
2 2
2
Using Maxwell equation : E , Dotting both sides with H:
H
H E H
2
1
Substitute in equation (1): H E H E
2
1
E H
2 2
1
E H
2 2
H
t
H
t t
E
E
t
H E
E
t t
E H
E
t



 

 

 

  

 
 
      
 
 
 

      

 
     
 
 
      

 
 
2 2 2
2 2 2
Take volume integral of both sides:
1 1
E H
2 2
Applying the divergence theorem to the left hand side:
1 1
E H
2 2
v v v
S v v
t
dv E H dv E dv
t
dS E H dv E dv
t
  
  

  
     
 
  
  
    
 
  
  
  

4. 4
  2 2 2
1 1
E H
2 2
S v v
dS E H dv E dv
t
  
  
     
 
  
  
Power and the Poynting Vector
Total power
leaving the
volume
Rate of decrease
in energy stored
in electric and
magnetic fields
Ohmic
power
dissipated
2
the (Watts/m ) is defined as:
=E×H
It represents the instantaneous power density vector
associated with the EM field at a given point.
PoyntingVector


5. 5
Power and the Poynting Vector
Poynting theorem: states that the net power flowing out of a given
volume v is equal to the time rate of decrease in the energy stored
with v minus the ohmic losses.
Illustration
of power
balance for
EM fields.
Note that is
normal to both E and
H and is therefore
along the direction
of propagation ak
=E×H


6. 6
 
 
   
 
   
0
0
0
0
2
2
2
2
Assume that
E( , ) cos -
H( , ) cos -
( , )= E H = cos - cos -
( , )= cos cos 2 - 2
2
1
since cosAcosB= cos cos
2
z
x
z
y
z
z
z
z
z t E e t z a
E
then z t e t z a
E
and z t e t z t z a
E
z t e t z a
A B A B






 
 
  

    

   






 
  
 
  
 
 
  
 
Power and the Poynting Vector

7.  
 
0
0
0
*
s s
2
2
2
2
The time-average Poynting vector ( ) over the period T=2 / is:
1
( ) ( , )
It can also be found by:
1
( ) Re E ×H
2
For ( , ) cos cos 2 - 2
2
( ) cos
2
ave
T
ave
ave
z
z
z
ave
z
z z t dt
T
z
E
z t e t z a
E
z e

 

 
   





  
 
 
   
 
  

The total time-average power crossing a given surface S is given by:
S
z
ave ave
S
a
P d


  

7
Power and the Poynting Vector

8.  
 
0
2
2
0
*
s s
2
( , , , ) Poynting vector
( , , ) time-average of Po
time-varying vector (watts/m )
( , , , ) E×H
(time-invariant vector) (watt
ynting
s/m )
1
( , , , )
1
Re E
vector
×H
2
( )
2
T
ave
ave
av
ave
e
x y z t
x y z t dt
T
E
x y z t
x y z
z e


 

  
 




 

 
 
2
0
total time-average power through
cos E cos -
(scalar) watts
a surface
S
z z
z x
ave av
e
e
v
S
a
a for E e t z a
P d
P
 

  
 


 


 8
Power and the Poynting Vector

9. 9
7
r
2
In a nonmagnetic medium
E = 4 sin (2 10 0.8 ) V/m
Find
(a) ,
(b) The time-average power carried by the wave
(c) The total power crossing 100 cm of plane 2x + y = 5
z
t x

 
  a
Example 10.7

10. 10
7
(a) Since =0 and /c, the medium is not free space but
a lossless medium.
0.8 , 2 10 , (nonmagnetic),
Hence
o o r
  
       
   

    
 
 
8
7
2
or
0.8 3 10 12
2 10
14.59
120
120 . 10 98.7
12
o o r r
r
r
o
o r r
c
c

   


  

   
  
   


  


      
Example 10.7 - Solution

11. 2
2
x
2
2
x x x
2
0
(b) sin ( )
1 16
81 mW/m
2 2 10
(c) On plane 2x + y = 5 (see Example 3.5 or 8.5),
2
5
Hence the total power is
o
T
o
ave
x y
n
av
E
t x
E
dt
T
P
 

 
   
     




E H a
a a a
a a
a
   
3 4
5
2
. . 81 10 . 100 10
5
162 10
724.5 W
5
x y
e ave ave n x
dS S

 


 
  
     
 

 

a a
a a
11
Example 10.7 - Solution

12. 12
10.8 Reflection of a plane wave
at normal incidence
When a plane wave from one medium meets a different medium, it
is partly reflected and partly transmitted.
The proportion of the incident wave that is reflected or transmitted
depends on the parameters (ε,μ,σ) of the two media involved.
Normal incidence (plane wave is normal to the boundary) and
oblique incidence will be studied.

13. 13
Reflection of a plane wave at normal incidence
Suppose a plane wave propagating along the +z direction is incident
normally on the boundary z=0 between medium 1 (z<0) characterised
by ε1,μ1,σ1 and medium 2 (z>0) characterised by ε2,μ2,σ2.

14. i i z
(E ,H ) is traveling along +a in medium 1.
Assume the electric and megnetic filed (in phasor form) as follows:
Incident Wave
14
Reflection of a plane wave at normal incidence
1
1 1
0
0
0
1
E ( ) a ,
H ( ) a a
z
is i x
z z
i
is i y y
z E e then
E
z H e e

 


 

 
0 is magnitude of
the incident electric
field at z=0
i
E

15. z
(E ,H ) is traveling along a in medium 1.
Reflected Wave
r r 
15
Reflection of a plane wave at normal incidence
 
1
1 1
0
0
0
1
If E ( ) a ,
H ( ) a a
z
rs r x
z z
r
rs r y y
z E e then
E
z H e e

 


   
0 is magnitude of
the reflected electric
field at z=0
r
E

16. z
(E ,H ) is traveling along +a in medium 2.
Transmitted Wave
t t
16
Reflection of a plane wave at normal incidence
2
2 2
0
0
0
2
If E ( ) a ,
H ( ) a a
z
ts t x
z z
t
ts t y y
z E e then
E
z H e e

 


 

 
0 is magnitude of
the transmitted electric
field at z=0
i
E

17. 1 1
2 2
Field in medium 1: E E E , H H H
Field in medium 2: E E , H H
Since the waves are transverse, E and H fields are entirely
tangential to the interface.
Applying the boundary
i r i r
t t
   
 


 
1t 2t 1t 2t
0 0 0 0 0
0
0 0
1 2
conditions at the interface 0:
(E =E and H =H )
:
E (0) E (0) E (0)
1
H (0) H (0) H (0)
i r t i r t
t
i r t i r
z
then
E E E
E
E E
 

    
    
17
Reflection of a plane wave at normal incidence

18. 2 1
0 0
2 1
0 2 1
0 0
0 2 1
2
0 0
2 1
0 2
0 0
0 2 1
From the last two equations:
= ,
Re or
2
2
= ,
flection Coeffici
or
ent
Transmission Coefficient
r i
r
r i
i
t i
t
t i
i
E E
E
E E
E
and E E
E
E E
E
 
 
 
 

 

 
 




    



  

Note that:
1. 1+
2. Both and are dimensionless and may be complex.
( and are real for lossless media, and complex for lossy media)
3. 0 1 (-1 1, 0 2)




 


        18
Reflection of a plane wave at normal incidence

19. When medium 1 is a perfect dielectric (lossless , σ1=0), and
medium 2 is a perfect conductor (σ2=∞):
η2= 0 → Γ=-1 → τ=0
The wave is totally reflected and there is no transmitted wave
(E2 = 0).
The totally reflected wave combines with the incident wave to
form a standing wave.
A standing wave "stands" and does not travel; it consists of two
travelling waves (Ei and Er) of equal amplitudes but in opposite
directions. 19
Reflection of a plane wave at normal incidence
0
For conductor = 45





20. 20
 
 
 
1 1
1 1
z z
1s is rs i0 r0
0
1 1 1 1
0
z z
1s i0
1s 0 1
1 1s
E =E +E = + a
But = = 1, =0, =0, =
E a
E 2 sin z a (since sin = )
2
Thus E =R
The standing wave in medium 1 is:
e E ,
x
r
i
j j
x
jA jA
i x
j t
E e E e
E
j
E
E e e
e e
or jE A
j
e
 
 

   




 
  

 
1 0 1
0
1 1
1
E =2 sin z sin a
2
Similarly, it can be shown that: H = cos z cos a
i x
i
y
or E t
E
t
 
 

Reflection of a plane wave at normal incidence

21. 21
Reflection of a plane wave at normal incidence
Standing waves E  2Eio sin 1z sin t ax. The curves 0, 1, 2, 3, 4, . . ., are,
respectively, at times t  0, T/8, T/4, 3T/8, T/2, . . . ; l  2/1.

22. 22
Standing Waves Examples
Standing wave on a string
http://www.walter-fendt.de/ph14e/stwaverefl.htm

23. Medium 1 : perfect dielectric 1=0
Medium 2: perfect dielectric 2=0
η1 and η2 are real and so are Γ and τ.
There is a standing wave in medium 1 but there is also a
transmitted wave in medium 2. (incident wave is partly reflected
and partly transmitted).
However, the incident and reflected waves have amplitudes that
are not equal in magnitude.
Two cases:
case 1: when η2 > η1
case 2: when η2 < η1
23
Reflection of a plane wave at normal incidence

24. 24
CASE 1
Medium 1 : perfect dielectric 1=0, Medium 2: perfect dielectric 2=0
2 1
2 1
2 1
0
If , , 0,
0
and are real
j o
e
 
 
 


    

     

1 1
1 1
1
1
2
2
1
E E E ( )
(1 )
E 1
j z j z
s is rs oi
j z j z
oi
j z
s oi
E e e
E e e
E e
 
 

 
 

    
  
   
 
1
2
1 1 max
1 max 1
max
1 max 1
E is maximum when 1 E 1
2 0,2 ,4 ,6 ...
0,1,2,3
or 0, ,2 ,3 ,... 2
j z
oi
e E
z n n
z n
z

     l
    

    
 
     
 
 
1
2
1 1 min
1 min 1 min
1
min
1
E is minimum when 1 E 1
3 5
2 ,3 ,5 ... or , , ...
2 2 2
(2 1) (2 1)
0,1,2,3
2 4
j z
oi
e E
z z
n n
z n

  
    
 l


     
   
 
    

25. 25
CASE 2
Medium 1 : perfect dielectric 1=0, Medium 2: perfect dielectric 2=0
2 1
2 1
2 1
If , , 0,
180
and are real
j o
e 
 
 
 


    

     

1 1
1 1
1
1
2
2
1
E E E ( )
(1 )
E 1
j z j z
s is rs oi
j z j z
oi
j z
s oi
E e e
E e e
E e
 
 

 
 

    
  
   
 
1
2
1 1 min
1 min 1
min
1 min 1
E is minimum when 1 E 1
2 0,2 ,4 ,6 ...
0,1,2,3
or 0, ,2 ,3 ,... 2
j z
oi
e E
z n
n
z n
z

    l

    

    
 
     
 
 
1
2
1 1 max
1 max 1 max
1
max
1
E is maximum when 1 E 1
3 5
2 ,3 ,5 ... or , , ...
2 2 2
(2 1)
(2 1)
0,1,2,3
2 4
j z
oi
e E
z z
n
n
z n

  
    
l



     
   


    

26. 26
Standing waves due to reflection at an interface between two lossless
media; l  2/1.

27. • Measures the amount of reflections, the more reflections, the
larger the standing wave that is formed.
• The ratio of |E1|max to |E1|min
or
 Since 0 |≤ |Γ|≤1, it follows that 1 ≤s ≤∞.
* When Γ=0, s=1, no reflection, total transmission.
* When |Γ|=1, s=∞, no transmission, total reflection.
 s is dimensionless, expressed in decibels (dB) as: s dB=20log10 s
27







1
1
min
1
max
1
min
1
max
1
H
H
E
E
s
1
1




s
s
Standing Wave Ratio, SWR

28. 8
1 8
1
2
2 1
2
10 1
3 10 3
120
4
.(4) 4
3
2
o
o o r r
o r
o
o r
c
c


  
       

 
 

 
  
  

 
 
  
  
Solution :
28
8
x
o o
r r
In freespace (z 0),a plane wave with
=10 cos(10 t )a mA/m
is incident normally on a lossless medium ( =2 , =8 ) in region z 0.
Determine the reflected wave , and th
i z

   



H
H E t t
e transmitted wave ,
H E
Example 10.8

29. 29
8
1 x
8
1 i
1
Given that =10 cos(10 t ) we expect that
= cos(10 t )
where and = =10
Hence, = 10 cos(
i
i io E
Ei Hi ki x z y io io o
i o
z
z
E H


 



     

H a
E E a
a a a a a a
E 8
1
2 1
2 1
8
r
10 t ) mV/m
2 1 1
Now = = ,
2 3 3
10 1
Thus cos 10 t + mV/m
3 3
from which we easily obtain as
y
ro o o
ro io
io o o
r o y
z
E
E E
E
z

 
 
   




   
 
 
   
 
a
E a
H
8
10 1
cos 10 t + mA/m
3 3
r x
z
 
   
 
H a
Example 10.8 – solution continued

30.  
8
2
Similarly,
4 4
1 or
3 3
Thus
cos 10 t +
where .Hence,
t
to
to io
io
t to E
Et Ei y
E
E E
E
E z


     

  
E a
a a a
8
8
40 4
cos 10 t mV/m
3 3
from which we obtain
20 4
cos 10 t mA/m
3 3
t o y
t x
z
z

 
  
 
 
 
 
 
 
E a
H a
30
Example 10.8 – solution continued

31. 31
x y
Given a uniform plane wave in air as
(a) Find
(b) If the wave encounters
=40 cos( t
a perfectly conducting plate norm
) + 30 sin(
al
to the z axis at z
t ) V/m
= 0, fi
i
i
z z
   
 
E a a
H
r r
nd the reflected wave and .
(c) What are the total and fields for z 0 ?
(d) Calculate the time-average Poynting vectors
for z 0 and z 0.

 
E H
E H
Example 10.9

32. 1 2
x 2 y
(a) This is similar to the problem in Example 10.3.
We may treat the wave as consisting of tw
=40 cos( t ) , = 30 sin( t
o waves and where
At
)
i i
i i
z z
   
 
E E
E
Solutio
a
n
a E
r
1
1
1
1 2
1
atmospheric pressure, air has = 1.0006 1.
Thus air
cos( t )
may be regarded as free space.
Let
40 1
120 3
1
i i i
i
i
H
i o
o
i o
o
z
H
E
H


 


 


  

H H H
H a
1 y
Hence = cos( t )
1
3
1
H k E z x y
i z

 
    

a a a a a a
H a
32
Example 10.9 -solution

33. 33
Example 10.9 -solution
2
2
2
2
2 2
Similarly,
where
30 1
= sin( t )
Hence
120 4
i i o H
H k E z y x
i o
i o
o
H
E
H
z
 
  

 
  
   
H a
a a a a a a
2 x
1 2 x y
= sin( t )
and
sin( t ) + cos( t )
1
4
1 1
4 3
This problem can also be solved using Method 2 of Example 10.
mA
3
/m
.
i
i i i
z
z z
 
   

 
 
     
H a
H H H a a

34. 2
2 1
2
(b) Since medium 2 is perfectly conducting,
1 <<
that is 1 , = 0
showing that the incident and fields are totally reflected.
= =
Hence, =
ro io io
r
E E E

 


 
  
 
E H
E x y
1 1
40 cos( t ) 30 sin( t ) V/m
1 1
H = cos( t ) sin( t ) A/m
3 4
(c) The total fields in air
and
can be shown to be standing wave.
The total
r y x
i r i r
z z
z z
   
   
 
   
  
   
a a
a a
E E E H H H
2 2
fields in the conductor are 0 , 0.
t t
   
E E H H 34
Example 10.9 -solution

35. 35
Example 10.9 -solution
   
2
2 2
1
1 k z z
1
2 2 2 2
z z
2 2
2
2 k z
2 2
(d) For z 0,
| | 1
[ ]
2 2
1
= 40 30 40 30 =0
240
For z 0,
| |
0
2 2
because the whole incident power is reflected.
s
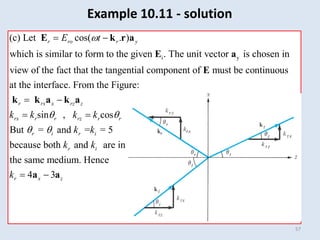
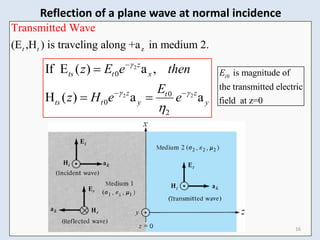
ave io ro
o
s to
ave
E
E E
E E
 

 

   
 
  
 

   
a a a
a a
a a

36. 36
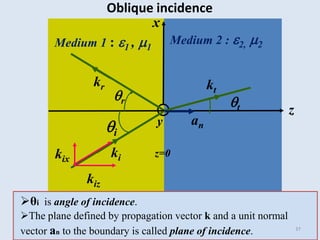
• Wave arrives at an angle.
• Assume lossless media.
• Uniform plane wave in general form
• For lossless unbounded media, k = 
( )
2 2 2 2 2
( , ) cos( ) Re[ ]
ˆ ˆ ˆ position vector
ˆ ˆ ˆ wave number or propagation vector
j t
o o
x y z
x x y y z z
x y z
E t E t E e
xa ya za
k a k a k a
k k k k


 
 
   
  
  
   
k r
r k r
r
k
Oblique incidence

37. z
y
z=0
Medium 1 : 1 , 1
Medium 2 : 2, 2
r
i
t
kr
ki
kt
kix
kiz
an
θi is angle of incidence.
The plane defined by propagation vector k and a unit normal
vector an to the boundary is called plane of incidence. 37
Oblique incidence
x

38. 38
1 1 1
2 2 2
1
1
E cos( )
E cos( )
E cos( )
cos
sin
i io ix iy iz
r ro rx ry rz
t to tx ty tz
i r
t
ix i
iz i
E k x k y k z t
E k x k y k z t
E k x k y k z t
where k k
k
k
k



   
   
 
 
   
   
   
  
 


ki =β1
kix
kiz
i
Oblique incidence

39. It's defined as E is || to incidence plane (E-field lies in the xz-plane)
39
Parallel Polarization

40.  
 
 
 
1
1
1
1
sin cos
sin cos
1
sin cos
sin cos
1
E (cos sin )
H
E (cos sin )
H
i i
i i
r r
r r
j x z
is io i x i z
j x z
io
is y
j x z
rs ro r x r z
j x z
ro
rs y
E e
E
e
E e
E
e
  
  
  
  
 

 

 
 
 
 
 

 
 
a a
a
a a
a
40
Parallel Polarization

41.  
 
2
2
sin cos
sin cos
2
E (cos sin )
H
t t
t t
j x z
ts to t x t z
j x z
to
ts y
E e
E
e
  
  
 

 
 
 

a a
a
41
Parallel Polarization

42. 42
Parallel Polarization
1 2
1
1 1 2
sin sin
sin
sin sin sin
1 1 2
Tangential components of E and H should be should be continuous
at the boundary z=0,
(cos ) (cos ) (cos )
i t
r
i i t
j x j x
j x
io i ro r to t
j x j x j x
io ro to
E e E e E e
E E E
e e e
   
 
     
  
  
 

  
 
 
1 1 2
1
The exponential terms must be equal for the previous equations
to be valid: sin sin sin
(Incidence angle = reflection angle)
i r t
i r
or
     
 


  

 1 1 1
2 2 2 2
sin
(snell's law)
sin
t
i
n
n
  
  
  

43. 43
1 1 2
2 1
|| ||
2 1
,
cos cos cos (x-components of E)
(y-component of H)
cos cos
,
cos cos
io i ro r to t
io ro to
ro t i
ro io
io t i
Hence
E E E
E E E
E
E E
E
  
  
   
   
 
 

    

Reflection coefficient
Transmission coefficient 2
|| ||
2 1
|| ||
2 cos
,
cos cos
cos
where (1 )
cos
to i
to io
io t i
i
t
E
E E
E
 
 
   



  

  
Parallel Polarization

44. 44
• defined as the incidence angle at which the reflection
coefficient is 0 (all transmission).
   
2 1 ||
||
2 1 ||
2 1 ||
2 2 2 2
2 1 ||
1 1
||
2 2
2 1 2 2 1
|| 2
1 2
Byt setting :
cos cos
0
cos cos
cos cos
1 sin 1 sin
sin
, and
sin
1 ( / )
sin
1 ( / )
i B
t B
t B
t B
t B
t
i B
i
B
or
Since
 
   
   
   
   
  
 
  
   

 
 

  

 
  
 

 

Parallel Polarization - Brewster angle, B

45. 45
Perpendicular Polarization
In this case, the E field is perpendicular to the plane of incidence
(the xz-plane)

46. 46
 
 
 
 
1
1
1
1
sin cos
sin cos
1
sin cos
sin cos
1
E
H ( cos sin )
E
H (cos sin )
i i
i i
r r
r r
j x z
is io y
j x z
io
is i x i z
j x z
rs ro y
j x z
ro
rs r x r z
E e
E
e
E e
E
e
  
  
  
  
 

 

 
 
 
 

  

 
a
a a
a
a a
Perpendicular Polarization

47. 47
Perpendicular Polarization
 
 
2
2
sin cos
sin cos
2
E
H ( cos sin )
t t
t t
j x z
ts to y
j x z
to
ts t x t z
E e
E
e
  
  
 

 
 

  
a
a a
(cos sin )
t x t z
 

a a

48. 48
i
1 1 2
components of E and H should be should be continuous
at the boundary z=0, and by setting = :
(y-component of E)
cos cos (x-component of H)
r
io ro to
io ro to
i t
Tangential
E E E
E E E
 
 
  

 
 
 
 
 
Reflect 2 1
2 1
2
2 1
cos cos
,
cos cos
2 cos
,
cos cos
where 1
ro i t
ro io
io i t
to i
to io
io i t
E
E E
E
E
E E
E
   
   
 
 
   

 
 
 

    

  

  
ion coefficient
Transmission coefficient
Perpendicular Polarization

49. 49
• For no reflection (total transmission):
   
2 1
2 1
2 1
2 2 2 2
2 1
1 1
2 2
2 2 1 1 2
2
1 2
Byt setting :
cos cos
0
cos cos
cos cos
1 sin 1 sin
sin
, and
sin
1 ( / )
sin
1 ( / )
i B
B t
B t
B t
B t
t
i B
i
B
or
Since
 
   
   
   
   
  
 
  
   

 








 

  

 
  
 

 

Perpendicular Polarization - Brewster angle

50. 50
Summary
Property Normal
Incidence
Perpendicular Parallel
Reflection
coefficient
Transmission
coefficient
Relation
i
t
i
t








cos
cos
cos
cos
1
2
1
2
||




t
i
i







cos
cos
cos
2
1
2
2



t
i
t
i








cos
cos
cos
cos
1
2
1
2




2
2 1
2

 

 i
t
i







cos
cos
cos
2
1
2
2
||


1
2
1
2










1
 
 

1
  
t
i



cos
cos
1 ||
|| 



51. 51
j(0.866y+0.5z)
s x
An EM wave travels in free space with the
electric field component
= 100e V/m
Determine
(a) and
(b) The magnetic field compone
(
nt
c
 l
E a
) The time average power in the wave
Example 10.10

52. 52
j( )
j
s o o x
2 2 2
(a) Comparing the given E with
= e = e
it is clear that
0 , 0.866 , 0.5
(0 8 6
. 6
x y z
k x k y k z
x x z
x y z
E
k k k
k k k k
 
  
   
k.r
E E a
2 2
8
) (0.5) 1
But in free space,
2
Hence, 3 10 rad/s
2
2 6.283 m
o o
k =
c
kc
k
 
   
l


l 
 
  
  
  
Example 10.10 -solution

53. 53
j(0.866 0.5 )
s
2 2
j
s x
j(0.866 0.5 )
s y z
(b) the corresponding magnetic field is given by
0.866a 0.5a
0.866 0.5
0.866 0.5
0.866 0.5
100 e
(0.132 0.23 ) e A/m
(c) The time averag
y z
k s
y z
k y z
y z
y z
a
a







  


 
 
E
H
a a
a a
H a
H a a
   
 
2
2
*
s s k y z
y z
e power is
100
1
= Re (0.866 +0.5 )
2 2 2 120
=11.49 + 6.631 W/m2
o
avg
E
 
   
E H a a a
a a
Example 10.10 -solution

54. 54
Example 10.11
r
y
A uniform plane wave in air with
= 8 cos V/m
is incident on a dielectric slab (z 0) with 1 , 2.5 , =0.
Find
(a) The polarization of the wave
(b) The angle of
( t 4 )
n
3
i
r
x z
  

  
 
E a
cidence
(c) The reflected field
(d) The transmitted field
E
H

55. 55
8
(a) From the incident field, it is evident that the propagation vector is
4 3 5
Hence, =5c=15 10 rad/s
A unit vector normal to the interface (z = 0)
i x z i o o
k
c

  

     

E
k a a
i
is .
The plane containing and is y = constant, which is the xz-plane,
the plane of incidence. Since is normal to this plane, we have
perpendicular polarization (similar to Figure 10.17).
z
z
a
k a
E
Example 10.11 - solution

56. i i
i i
n
i
4
(b) from the figure, tan 53.13
3
Alternatively, we can obtain from the fact that
is the angle between and , that is,
cos .
4 3
5
o
ix
iz
k n
x z
 
 

   



 

k
k
k a
a a
a a
i
3
.
5
or 53.13
z
o






a
56
Example 10.11 - solution

57. 57
i y
(c) Let cos( . )
which is similar to form to the given . The unit vector is chosen in
view of the fact that the tangential component of must be continuous
at the interface. From t
r ro r y
E t

 
E k r a
E a
E
he Figure:
sin , cos
But = and = = 5
because both and are in
the same medium. Hence
4 3
r rx x rz z
rx r r rz r r
r i r i
r i
r x z
k k k k
k k
k k
k
 
 
 
 
 
k k a k a
a a
Example 10.11 - solution

58. 58
0
1 1
1
2 2 2
2 1
2 1
0 2
1 0 2
2
To find , we need . From Snell's law
sin53.13
sin sin sin
2.5
or 30.39
cos cos
cos cos
377
where 377 , 238.4
2.5
r t
o
t i i
o
t
ro i t
io i t
r
o r
ro
io
E
c
n
n c
E
E
E
E

 
  
 

   
   
 
  
 


  


  

    
  
8
238.4cos53.13 377cos30.39
0.389
238.4cos53.13 377cos30.39
Hence, 0.389(8) 3.112
3.112cos(15 10 4 3 ) V/m
o o
o o
ro io
r y
E E
t x z


 

     
    
E a
Example 10.11 - solution

59. 59
8
2 2 2 2 2 8
(d) Similarly, let the transmitted electric field be
cos( . )
15 10
where 1 2.5 7.906
3 10
From the Figure ,
sin =4
cos 6.819
4 6.819
No
t to t y
t r r
tx t t
tz t t
t x z
E t
k
c
k k
k k


     


 

     


 
 
E k r a
k a a
2
2 1
tice that
2 cos
cos cos
2 238.4cos53.13
0.611
238.4cos53.13 377cos30.39
ix rx tx
to i
io i t
o
o o
k = k = k
E
E
 

   
  


 

Example 10.11 - solution

60. 60
8
t t
t
t
2
The same result could be obtained from the relation =1+ . Hence,
0.611 8 4.888
4.88cos(15 10 4 6.819 )
From , is easily obtained as
4 6.819
4.888 cos
7.906(238.4)
t
to io
t y
k x z
y
E E
t x z





   
   
 
  
E a
E H
a E a a
H a
8
t
( . )
( 17.69 10.37 )cos(15 10 4 6.819 ) mA/m
r
x z
t
t x z
 
     
k r
H a a
Example 10.11 - solution