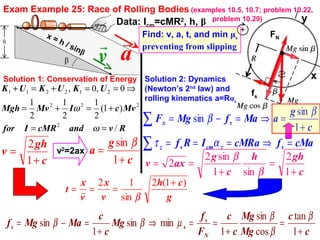
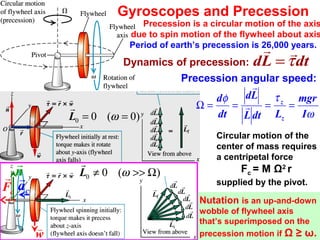
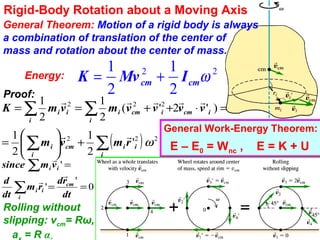
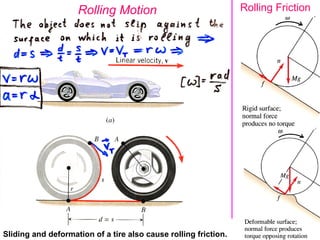
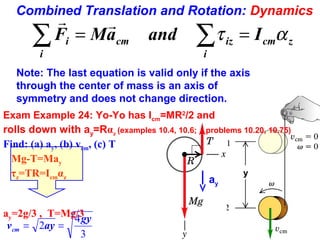
1) The document discusses dynamics of rotational motion, including Newton's second law for rotation which states that torque equals the product of moment of inertia and angular acceleration. 2) It defines important rotational concepts like torque, angular momentum, moment of inertia, and establishes relationships between them using principles like conservation of energy and angular momentum. 3) Examples are provided to demonstrate applications of rotational dynamics like rolling motion without slipping, combined translation and rotation, gyroscopes and precession. Analogies between rotational and translational motions are also highlighted.

1. Dynamics of Rotational Motion
The main problem of dynamics: How a net force affects
(i) translational (linear) motion (Newtons’ 2nd
law)
(ii) rotational motion ???
(iii) combination of translational
and rotational motions ???
amF

=⇒
m F

αz
Axis of
rotation
a

Level arm l is the distance between the
line of action and the axis of rotation,
measured on a line that is to both.⊥
Definition of torque: Fr

×=τ
A torque applied to a door
Units: [ τ ] = newton·meter = N·m
τz > 0 if the force acts counterclockwise
τz < 0 if the force acts clockwise

2. Newton’s Second Law for Rotation about a Fixed Axis
(i) One particle moving on a circle: Ftan=matan and atan= rαz
rFtan= mr2
αz τz = I αz
Only Ftan contributes to the torque τz .
τz I
(ii) Rigid body (composed of many particles m1, m2, …)
zzz
i i
iiiz Irm ατατ =⇒





=∑ ∑ 2
Only
external
torques
(forces)
count !
Example 10.3: a1x,T1,T2? a1x
a2y
y
Pulley: T2R-T1R=Iαz
a1x=a2y=Rαz
X
T2-T1=(I/R2
)a1x
Glider: T1=m1a1x
Object: m2g-T2=m2a1x
2
21
21
2
2
21
21
1
2
21
2
1
/
)(
/
/
RImm
gmMm
T
RImm
gmm
T
RImm
gm
a x
++
+
=
++
=
++
=

3. Work-Energy Theorem and Power in Rotational Motion
Rotational work:
∫=
⇒===
2
1
tantan
θ
θ
θτ
θτθ
dW
dRdFdsFdW
zR
zR
θτθθττ ∆=−=⇒= zzRz WconstFor )( 12
Work-Energy Theorem for Rigid-Body Rotation:
12
2
1
2
2
2
1
2
1
2
1
RRzzR KKIIdIW −=−== ∫
ω
ω
ωωωω
Power for rotational work or energy change:
)( vFPofganaloP
dt
d
dt
dW
P zzRz
R
R

⋅==⇒== ωτ
θ
τ
zz
z
z dI
dt
dd
Id ωω
θω
θτ ==Proof:

4. Rigid-Body Rotation about a Moving Axis
22
2
1
2
1
ωcmcm IMvK +=
Proof:
General Theorem: Motion of a rigid body is always
a combination of translation of the center of
mass and rotation about the center of mass.
( )∑∑
∑ ∑
+





=
=⋅++==
i
iicm
i
i
icm
i i
icmiii
rmvm
vvvvmvmK
222
222
'
2
1
2
1
)'2'(
2
1
2
1
ω


Rolling without
slipping: vcm= Rω,
a = R α
Energy:
General Work-Energy Theorem:
E – E0 = Wnc , E = K + U
∑
∑
==
=
i
cm
ii
ii
dt
rd
rm
dt
d
vmncesi
0
'
'
'




5. Rolling Motion Rolling Friction
Sliding and deformation of a tire also cause rolling friction.

6. Combined Translation and Rotation: Dynamics
∑∑ ==
i
zcmiz
i
cmi IandaMF ατ

Note: The last equation is valid only if the axis
through the center of mass is an axis of
symmetry and does not change direction.
Exam Example 24: Yo-Yo has Icm=MR2
/2 and
rolls down with ay=Rαz (examples 10.4, 10.6; problems 10.20, 10.75)
Find: (a) ay, (b) vcm, (c) T
Mg-T=May
τz=TR=Icmαz
ay=2g/3 , T=Mg/3
ay
3
4
2
gy
ayvcm ==
y

7. Exam Example 25: Race of Rolling Bodies (examples 10.5, 10.7; problem 10.22,
problem 10.29)
β v

a

Data: Icm=cMR2
, h, β
Find: v, a, t, and min μs
preventing from slipping
y
xSolution 1: Conservation of Energy Solution 2: Dynamics
(Newton’s 2nd
law) and
rolling kinematics a=Rαz
RvandcMRIfor
MvcIMvMgh
UKUKUK
/
)1(
2
1
2
1
2
1
0,0,
2
222
212211
==
+=+=
⇒==+=+
ω
ω
c
gh
v
+
=
1
2
x = h / sinβ
v2
=2ax
c
g
a
+
=
1
sin β
g
ch
v
x
v
x
t
)1(2
sin
12 +
===
β
fs
c
c
Mg
Mg
c
c
F
f
Mg
c
c
MaMgf
N
s
ss
+
=
+
==⇒
+
=−=
1
tan
cos
sin
1
minsin
1
sin
β
β
β
µββ
FN
∑
∑
=⇒===
+
=⇒=−=
cMafcMRaIRf
c
g
aMafMgF
szcmsz
sx
ατ
β
β
1
sin
sin
c
ghh
c
g
axv
+
=
+
==
1
2
sin1
sin2
2
β
β

8. Angular Momentum
(i) One particle: φsinmvrLvmrprL =⇒×=×=

τ






=×=⇒×=





×+





×= Fr
dt
Ld
amr
dt
vd
mrvm
dt
rd
dt
Ld
0)( =×vvm

(ii) Any System of Particles: ∑ ∑=⇒=
i
i
dt
Ld
LL τ



It is Newton’s 2nd
law
for arbitrary rotation.
Note: Only external torques count
since .0∑ =ternalinτ

(iii) Rigid body rotating
around a symmetry axis:
(nonrigid or rigid bodies)
( )∑ ∑ =⇔=== ωωω

ILIrmLL zziiiz
2
Unbalanced wheel: torque of friction in bearings.
∑ =⇒=== zzz
zz
II
dt
d
I
dt
dL
andconstI ατα
ω
Impulse-Momentum Theorem for Rotation

9. Principle of Conservation of Angular Momentum
Total angular momentum of a system is constant (conserved),
if the net external torque acting on the system is zero:
∑∑ ==⇔=⇒= 00 ττ




ifconstL
dt
Ld
dt
Ld
Example: Angular acceleration due to sudden
decrease of the moment of inertia
f
f
f IIncesi
I
I
>>= 000
0
ωωω
For a body rotating around a symmetry axis:
I1ω1z = I2ω2z
ω0 < ωf
Origin of Principles of Conservation
There are only three general principles of conservation
(of energy, momentum, and angular momentum) and
they are consequences of the symmetry of space-time
(homogeneity of time and space and isotropy of space).

10. I n [ 2 8 ] : = f s _ :  N I n t e g r a t e 1 S q r t 1  x  x  s  x  6  s , x , 0 , s ;
P l o t f s , 1 , s , 0 , 1 
O u t [ 2 9 ] =
0 .2 0 .4 0 .6 0 .8 1 .0
1 .0
1 .1
1 .2
Hinged board (faster than free fall)
α
h=L sinα
Mg
m Ball: 0
2
sin)/2(/22/ αgLvhtmvmgh ball ==⇒=
Board: I=(1/3)ML2
∫
∫
−−
=
−
=
−=−
≡=
−
0
0
sin
0 0
2
0
0 0
0
222
0
))(sin1(sin6
1
sinsin3
)sin(sin
3
2
)/(
322
α
α
αα
αα
α
αα
α
αω
xx
dx
t
t
d
g
L
t
L
g
dt
d
dtdMLIhh
Mg
ball
cup
cup
0sinα
ball
cup
t
t
0
0 50≈αCritical3/2

11. Gyroscopes and Precession
cF

ca

)0(00 == ωL

)(00 Ω>>≠ ωL

w

n

Dynamics of precession: dtLd τ

=
Precession is a circular motion of the axis
due to spin motion of the flywheel about axis
Precession angular speed:
ω
τφ
I
mgr
LdtL
Ld
dt
d
z
z
====Ω 

Circular motion of the
center of mass requires
a centripetal force
Fc = M Ω2
r
supplied by the pivot.
Nutation is an up-and-down
wobble of flywheel axis
that’s superimposed on the
precession motion if Ω ≥ ω.
Period of earth’s precession is 26,000 years.

12. Analogy between Rotational and Translational Motions
Physical Concept Rotational Translational
Displacement θ s
Velocity ω v
Acceleration α a
Cause of acceleration Torque τ Force F
Inertia Moment of
inertia I = Σmr2
Mass m
Newton’s second law Στ = I α ΣF = ma
Work τ θ Fs
Kinetic Energy (1/2) Iω2
(1/2) mv2
Momentum L = I ω p = mv