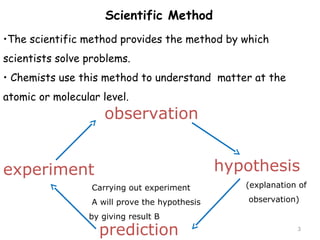
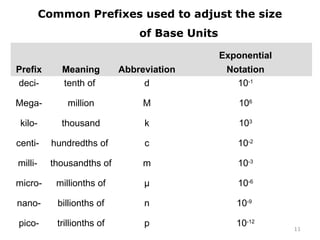
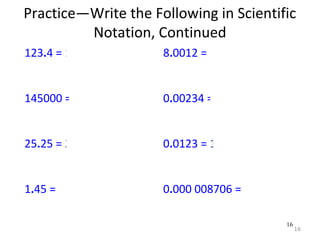
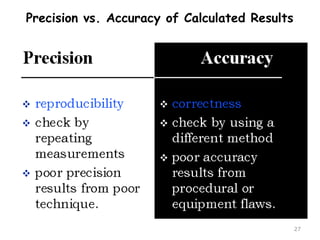
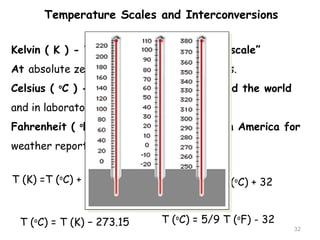
This document provides an introduction to CHEM 1101 and covers several key chemistry concepts. It introduces the instructor, Dr. Muhannad Amer, and discusses the scientific method and how it is used in chemistry. It also defines and compares scientific theories and laws. Additionally, it covers important topics such as the International System of Units (SI units), dimensional analysis, density, temperature scales, and significant figures.

1. 1
Welcome to CHEM 1101
Instructor: Dr. Muhannad Amer
Office Location: 44 staff Bldng

2. 2
• Beyond the chemistry theory of this class
taking this class will enable you to:
•Apply knowledge to solve new problems.
• Analyze information you have gathered.
• Work with and delegate responsibility to others.
• Have confidence in yourself and your work.
• Be organized in your thoughts and actions.
• Ask and answer questions.

3. 3
•The scientific method provides the method by which
scientists solve problems.
• Chemists use this method to understand matter at the
atomic or molecular level.
observation
hypothesis
prediction
experiment
Scientific Method
(explanation of
observation)
Carrying out experiment
A will prove the hypothesis
by giving result B

4. 4
TThheeoorryy
• WWhheenn ccoonnssiisstteennccyy iiss oobbttaaiinneedd,,
hhyyppootthheesseess bbeeccoommee aa tthheeoorryy
• Typically a fact of nature, often a math
constant/number and unit.
– Law of Conservation of Mass— “In a chemical
reaction matter is neither created nor destroyed.”
– Speed of Light, E = mc2, Dalton’s Gas Law,
Universal Gas Constant, etc…

5. 5
Theories
• Explains how nature behaves.
– Newton’s Gravitational Theory: how an apple falls
– Dalton’s Atomic Theory: atoms look like…
– Darwin’s Theory of Evolution: we always change
– Einstein's Theory of Relativity: light is constant
• Used to predict future observations.

6. 6
6
What’s the Difference Between a
Law and a Theory?
• Laws: Very specific, “What will happen” often
expressed in mathematical equations.
• Theories: Very general, “Why it will happen,”
often includes many “Laws”

7. 7
•Observations
•Observations can be quantitative(wwhhiicchh iinnvvoollvvee nnuummbbeerrss..))
• or qualitative (cchhaannggeess iinn ccoolloorr aanndd pphhyyssiiccaall ssttaattee))
•All measurements MUST consist of
• a number and a unit!
•Example: charge of an electron is 1.60 x 10-19 coulombs
•Scientific notation
•1.60 x 10-19 = 0.000000000000000000160

8. 8
Scientific Notation
number x 10n
1-9
integer
0
1.60 x 10 = 1.60 x 1 = 1.60
1.60 x 101 = 16.0
1.60 x 10-1 = 0.160
1.60 or 1.6 or 1.600 can be used

9. 9
Are Units of Measurement that Important?
July 23rd, 1983: Gimli Glider, an Air Canada aircraft ran out of
fuel
Needed for trip: 22,300 kg of fuel
Used to fill plane: 22,300 pounds of fuel (10,115 kg !)
Not enough fuel!

10. Important SI (International system) base units
10
Quantity SI Base Unit
Length meter (m)
Mass kilogram (kg)
Time second (s)
Temperature Kelvin (K)
Amount mole (mol)
Volume = length3
1L = 1 dm3 = 1000 cm3 = 10-3 m3 = 1000 ml
1cm3 = 1ml

11. 11
Common Prefixes used to adjust the size
of Base Units
Prefix Meaning Abbreviation
Exponential
Notation
deci- tenth of d 10-1
Mega- million M 106
kilo- thousand k 103
centi- hundredths of c 10-2
milli- thousandths of m 10-3
micro- millionths of μ 10-6
nano- billionths of n 10-9
pico- trillionths of p 10-12

12. 12
Uncertainty in Measurement
The number obtained in measurement
is obtained using a measuring device that
introduces some degree of uncertainty
to this measurement and this must be
indicated.
Uncertainty in the measurement lies in the
last digit and is assumed to be +1 or -1
Recorded measurement of 0.0508 g
Actual mass is 0.0507 g or 0.0509 g
= 5.07 x 10-2 or 5.09 x 10-2 g

13. The recorded certain and the first uncertain digit or
estimated number of a measurement are called its significant
figures.
13
Significant Figures
Rules for Significant Figures
1. Digits from 1-9 are always significant.
Example: 26981 has 5 significant figures
2. Zeros between two other significant digits are always
significant. Example: 1023 has 4 significant figures
3. One or more additional zeros to the right of both the
decimal place and another significant digit are significant.
Example: 5.00 and 500. both have 3 significant figures

14. 14
Significant Figures
4. Zeros used solely for spacing the decimal point (placeholders)
are not significant.
Example: 0.000231 has 3 significant figures
5. The absence of a decimal point means terminal zeros
are NOT significant.
Example: 600 has 1 significant figure
6. Exact numbers have an infinite number of significant
figures. They are obtained via counting, e.g. 1 dozen eggs,
or by definition, e.g. the 2 in 2pr. When used in calculations,
exact numbers do not limit the number of significant figures.

15. 15
How many significant figures are in
each of the following measurements?
24 mL 2 significant figures
3001 g 4 significant figures
0.0320 m3 3 significant figures
6.4 x 104 molecules 2 significant figures
560 kg 2 significant figures
1.8

16. Practice—Write the Following in Scientific
16
16
Notation, Continued
123.4 = 1.234 x 102
145000 = 1.45 x 105
25.25 = 2.525 x 101
1.45 = 1.45 x 100
8.0012 = 8.0012 x 100
0.00234 = 2.34 x 10-3
0.0123 = 1.23 x 10-2
0.000 008706 = 8.706 x 10-6

17. 17
Tro's "Introductory Chemistry",
Chapter 2
17
Practice—Write the Following in
Standard Form, Continued
2.1 x 103 = 2100
9.66 x 10-4 = 0.000966
6.04 x 10-2 = 0.0604
4.02 x 100 = 4.02
3.3 x 101 = 33
1.2 x 100 = 1.2

18. 18
Determine the Number of Significant Figures,
• 12000
18
• 120.
• 12.00
• 1.20 x 103
• 0.0012
• 0.00120
• 1201
• 1201000
2
3
4
3
2
3
4
4

19. 19
How man y sig figs?
45.8736
.000239
.00023900
48000.
48000
3.982´106
1.00040
6
3
5
5
2
4
6
•All digits count
•Leading 0’s don’t
•Trailing 0’s do
•0’s count in decimal form
•0’s don’t count w/o decimal
•All digits count
•0’s between digits count as well
as trailing in decimal form

20. 20
Significant Figures
1.8
Addition or Subtraction
The answer cannot have more digits to the right of the decimal
point than any of the original numbers.
89.332
+1.1
90.432 round off to 90.4
one significant figure after decimal point
3.70
-2.9133
0.7867
two significant figures after decimal point
round off to 0.79

21. Multiplication or Division
The number of significant figures in the result is set by the original
number that has the smallest number of significant figures
21
Significant Figures
1.8
4.51 x 3.6666 = 16.536366 = 16.5
3 sig figs round to
3 sig figs
6.8 ÷ 112.04 = 0.0606926
2 sig figs round to
2 sig figs
= 0.061

22. Exact Numbers
Numbers from definitions or numbers of objects are considered
to have an infinite number of significant figures
22
Significant Figures
1.8
The average of three measured lengths; 6.64, 6.68 and 6.70?
6.64 + 6.68 + 6.70
3
= 6.67333 = 6.67
Because 3 is an exact number
= 7

23. = 5946.50525 Seen on
calculator
but not to be
recorded as
the answer
23
Multiplying and Dividing Significant Figures
22.37 x 3.10 x 85.75
4 sig. figs 3 sig. figs 4 sig. figs
5950
Least number of significant
figures dictates the number
of significant figures to be
stated in the calculated answer
5946.50525
9 sig. figs
5950
3 sig. figs
Rounding ³ 5 round up < 5 round down
Calculated results are never more reliable than the
measurements they are obtained from.

24. = 20.69 Seen on calculator but
24
Adding and Subtracting Significant Figures
3.76 + 14.83 + 2.1
2 dec.
2 dec.
places
places
1 dec.
place
not to be recorded as
the answer.
Least number of decimal places
dictates the number of decimal
places to be stated in the
calculated answer.
20.69
2 dec.
places
20.7
1 dec.
place
= 20.7
Rounding to
one dec.
place
Calculated results are never more reliable than the
measurements they are obtained from.

25. Addition (subtraction) with Multiplication (Division)
732.11 + 6.3
(Not to be recorded as
the answer)
25
760.00
do addition (subtraction) first
732.11 + 6.3 =
2 decimal
place
1 decimal
place
738.41 NEVER round
intermediate results for
multistep calculations
(738.4)
do division (multiplication) last
738.4
760.00
4 sig fig
5 sig fig
738.41
760.00
= 0.971592105
Answer: 0.9716 (4 sig fig)

26. 26
Examples of Rounding
For example you want a 4 Sig Fig number
4965.03
780,582
1999.5
0 is dropped, it is <5
8 is dropped, it is >5; Note you
must include the 0’s
5 is dropped it is = 5; note you
need a 4 Sig Fig
4965
780,600
2000.

27. 27
Precision vs. Accuracy of Calculated Results

28. Accuracy = Closeness of measured value to standard value
28
Precision = reproducibility
How much of a clone are
you?
Standard values
Sugar content: 54 grams
pH: 2.6
How do you measure
up?

29. 29
Dimensional Analysis
A problem-solving method that uses the fact that any
number or expression can be multiplied by one without
changing its value.
Unit factors may be made from any two terms that
describe the same or equivalent "amounts" of what we
are interested in.
1 inch = 2.54 centimeters
Unit factors

30. 30
Steps for Using Dimensional Analysis
Steps:
1.Identify what units are required, what units have been
given.
2. State the equivalent of these units.
3. Multiply the given data and its units by the appropriate
unit factors so that only the desired units are present
at the end.

31. Example: How many centimeters are in 6.00 inches?
Units required: centimeters
Units given : inches
Notice that the unit factor was chosen that allowed the
units required to remain while the other cancels
during the calculation.
31
1 inch = 2.54 centimeters
Unit factors

32. Kelvin ( K ) - The “Absolute temperature scale”
At absolute zero and only has positive values.
Celsius ( oC ) - Commonly used scale around the world
and in laboratories.
Fahrenheit ( oF ) - Commonly used scale in America for
weather reports.
32
Temperature Scales and Interconversions
T (K) =T (oC) + 273.15
T (oC) = T (K) − 273.15
T (oF) = 9/5 T (oC) + 32
T (oC) = 5/9 T (oF) - 32

33. 33
Density
Density is the mass per unit volume of a substance and has
compound units of grams per cubic centimeter (g/cm3)
Example: Calculate the density of an object that has a
volume of 64 cm3 and a mass of 34g.
Density = mass
volume
Solution:
Density = 34g
64cm3
= 0.53g/cm3

34. What is the mass, in grams, of 1.00 gallon of water ?
The density of water is 1 g/mL (1 ml of water = 1g)
1.057 qt = 1 L
given required
All equivalent values are EXACT numbers and do not limit the
number of significant figures in the answer.
34
Solution
Units given: gallon, g/ml Units required: g
1 gal = 4 qt
1.00 gal x
=
4 qts
1 gal
1 L = 1000 ml 1 g = 1 mL
x 1 L
1.057 qts
x 1000 mL
1 L
x 1 g
3 sig figs 1 mL
3784.295 = 3.78 x 103 g
calculator
= 3780 g
3 sig figs

35. 35
Quiz 1
• Perform the following mathematical operations
and express the result to the correct number of sf.
0.102 + 0.0821+ 2.73
1.01
• The volume of a diamonds is found to be 2.8ml .
What is the mass of the diamond in carats ?
1 carat = 0.200g . The density of diamond is
3.51 g/cm3 .