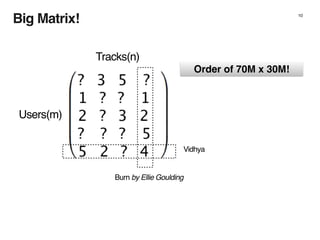
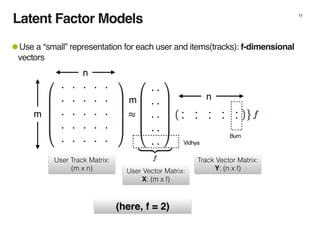
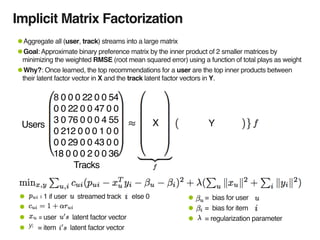
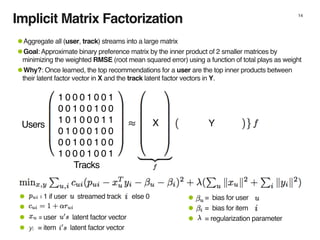
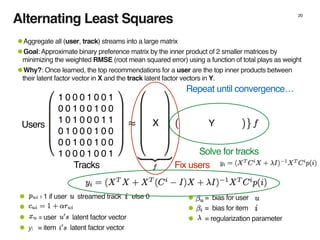
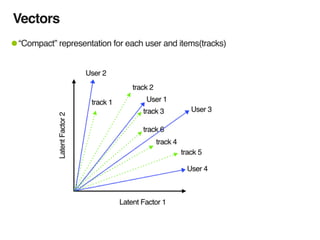
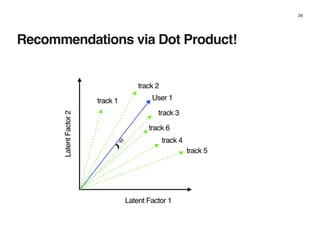
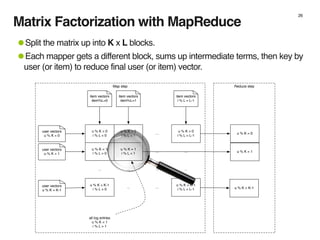
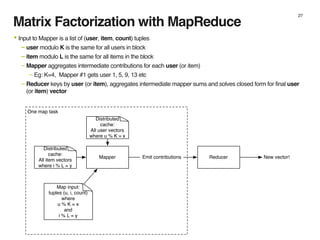
The document discusses music recommendation systems at Spotify, detailing the scale of its data operations and various approaches to recommending tracks, including collaborative filtering and matrix factorization. It highlights the challenges of predicting user preferences given the vast catalog of songs and the presence of implicit feedback from user behavior. Additionally, it outlines the use of MapReduce for efficient computation of user and track vectors to improve recommendation accuracy.

1. September 27, 2015
Music Recommendations
@
Spotify
Vidhya Murali
@vid052

2. Vidhya Murali
Areas of Interest: Machine Learning & Big Data
Data Science Engineer @ Spotify
Grad Student from the University of Wisconsin Madison
aka Happy Badger for life!
Who Am I?
2

3. Spotify’s Big Data
Started in 2006, now available in 58 countries
70+ million active users, 20+ million paid subscribers
30+ million songs in our catalog, ~20K added every day
1.5 billion playlists so far and counting
1 TB of user data logged every day
Hadoop cluster with 1500 nodes
~20,000 Hadoop jobs per day
3

4. Music Recommendations at Spotify
Features:
Discover
Discover Weekly
Right Now
Radio
Related Artists
4

5. 30 million tracks…
What to recommend?
5

6. Approaches 6
•Manual curation by Experts
•Editorial Tagging
•Metadata (e.g. Label Provided data, NLP over News,
Blogs)
•Audio Signals
•Collaborative Filtering Model

7. Collaborative Filtering Model 7
•Find patterns from user’s past behavior to generate
recommendations
•Domain independent
•Scalable
•Accuracy(Collaborative Model) >= Accuracy(Content
Based Model)

8. Definition of CF
8
Hey,
I like tracks P, Q, R, S!
Well,
I like tracks Q, R, S, T!
Then you should check out
track P!
Nice! Btw try track T!
Legacy Slide of Erik Bernhardsson

9. The YoLo Problem
9
•YoLo Problem: “You Only Listen Once” to judge recommendations
•Goal: Predict if users will listen to new music (new to user)
•Challenges
•Scale of catalog (30M songs + ~20K added every day)
•Repeated consumption of music is not very uncommon
•Music is niche
•Strong correlation between music consumption and user’s context
•Input: Feedback is implicit through streaming behavior, collection adds,
browse history, search history etc

10. Big Matrix! 10
Tracks(n)
Users(m)
Vidhya
Burn by Ellie Goulding
Order of 70M x 30M!

11. Latent Factor Models 11
Vidhya
Burn
.. . . . .
.. . . . .
.. . . . .
.. . . . .
.. . . . .
•Use a “small” representation for each user and items(tracks): f-dimensional
vectors
.. .
.. .
.. .
.. .
. .
...
...
...
...
..
(here, f = 2)
m m
n
m n
User Vector Matrix:
X: (m x f)
Track Vector Matrix:
Y: (n x f)
User Track Matrix:
(m x n)

12. Equation(s) Alert!
12

13. Implicit Matrix Factorization
8 0 0 0 22 0 0 54
0 0 22 0 0 47 0 0
3 0 76 0 0 0 4 55
0 212 0 0 0 1 0 0
0 0 29 0 0 43 0 0
18 0 0 0 2 0 0 36
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
X YUsers
Tracks
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vectoryi

14. Implicit Matrix Factorization 14
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
X YUsers
Tracks
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vectoryi

15. Alternating Least Squares 15
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
X YUsers
Tracks
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vector
Fix tracks
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
yi

16. 16
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
X YUsers
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vector
Fix tracks
Solve for users
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
Alternating Least Squares
yi
Tracks

17. 17
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
X YUsers
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vector
Fix users
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
Alternating Least Squares
yi
Tracks

18. 18
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
X YUsers
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vector
Fix users
Solve for tracks
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
Alternating Least Squares
yi
Tracks

19. 19
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
X YUsers
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vector
Fix users
Solve for tracks
Repeat until convergence…
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
Alternating Least Squares
yi
Tracks

20. 20
1 0 0 0 1 0 0 1
0 0 1 0 0 1 0 0
1 0 1 0 0 0 1 1
0 1 0 0 0 1 0 0
0 0 1 0 0 1 0 0
1 0 0 0 1 0 0 1
X YUsers
• = bias for user
• = bias for item
• = regularization parameter
• = 1 if user streamed track else 0
•
• = user latent factor vector
• = item latent factor vector
Fix users
Solve for tracks
Repeat until convergence…
•Aggregate all (user, track) streams into a large matrix
•Goal: Approximate binary preference matrix by the inner product of 2 smaller matrices by
minimizing the weighted RMSE (root mean squared error) using a function of total plays as weight
•Why?: Once learned, the top recommendations for a user are the top inner products between
their latent factor vector in X and the track latent factor vectors in Y.
Alternating Least Squares
yi
Tracks

21. 21
Alternating Least Squares
• the same for all users so compute only once per iteration
• weighted sum of outer products for item vectors the user
streamed
• weighted sum of item vectors the user streamed
•Key takeaways: requires O(f^2) memory, time complexity linear in number of
unique items the user streamed
f x f f x f f x 1f x f

22. Vectors
•“Compact” representation for users and items(tracks)

23. Why Vectors? 23
•Compact musical representation of users’ taste, tracks’ genome
•Vectors encode higher order dependencies so even if users who listen to Rihanna
and don’t necessarily listen to Beyonce, the vectors will understand this dependency
(based on some higher order dependency down the line)
•Item-Item and User-Item scores computed using cosine distance
•Linear complexity based on the number of latent factors
• Easy to scale up

24. Recommendations via Dot Product!
24

25. 70 Million users x 30
Million tracks. How to
scale?
25

26. Matrix Factorization with MapReduce
26
Reduce stepMap step
u % K = 0
i % L = 0
u % K = 0
i % L = 1
...
u % K = 0
i % L = L-1
u % K = 1
i % L = 0
u % K = 1
i % L = 1
... ...
... ... ... ...
u % K = K-1
i % L = 0
... ...
u % K = K-1
i % L = L-1
item vectors
item%L=0
item vectors
item%L=1
item vectors
i % L = L-1
user vectors
u % K = 0
user vectors
u % K = 1
user vectors
u % K = K-1
all log entries
u % K = 1
i % L = 1
u % K = 0
u % K = 1
u % K = K-1
•Split the matrix up into K x L blocks.
•Each mapper gets a different block, sums up intermediate terms, then key by
user (or item) to reduce final user (or item) vector.

27. Matrix Factorization with MapReduce
27
One map task
Distributed
cache:
All user vectors
where u % K = x
Distributed
cache:
All item vectors
where i % L = y
Mapper Emit contributions
Map input:
tuples (u, i, count)
where
u % K = x
and
i % L = y
Reducer New vector!
•Input to Mapper is a list of (user, item, count) tuples
– user modulo K is the same for all users in block
– item modulo L is the same for all items in the block
– Mapper aggregates intermediate contributions for each user (or item)
– Eg: K=4, Mapper #1 gets user 1, 5, 9, 13 etc
– Reducer keys by user (or item), aggregates intermediate mapper sums and solves closed form for final user
(or item) vector

28. Annoy
70 million users, at least 4 million
tracks for recommendations.
Given user vector and track
vector, still tricky to find recs
Brute force approach: O(70M x
4M x 40) = 0(12 peta-operations)!
Approximate Nearest Neighbor
Oh Yeah! : Local Sensitive
Hashing
https://github.com/spotify/annoy
28

29. 29

30. Thank You!
You can reach me @
Email: vidhya@spotify.com
Twitter: @vid052