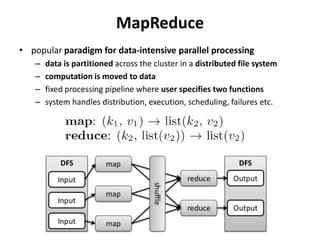
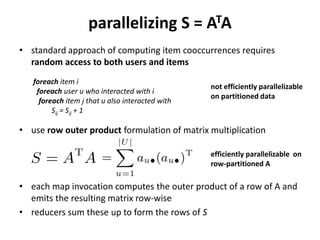
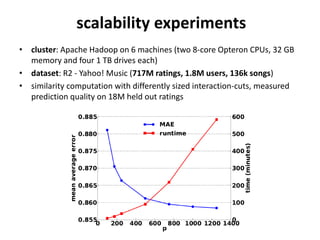
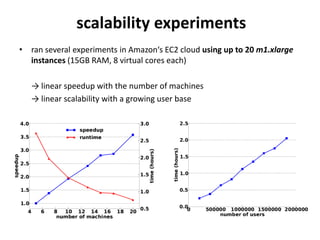
This document summarizes a research paper that proposes using MapReduce to scale up similarity-based neighborhood recommendation methods. The authors rephrase these algorithms to be efficiently parallelized across large datasets. They express common similarity measures like Jaccard coefficient in terms of canonical functions that can be embedded in their MapReduce approach. Experiments on a Yahoo! Music dataset with over 700 million ratings showed their method provided linear speedup and scalability with increasing data and cluster size.

1. Scalable Similarity-Based Neighborhood
Methods with MapReduce
6th ACM Conference on Recommender Systems, Dublin, 2012
Sebastian Schelter, Christoph Boden, Volker Markl
Database Systems and Information Management Group
Technische Universität Berlin

2. motivation
• with rapid growth in data sizes, the processing efficiency,
scalability and fault tolerance of recommender systems in
production become a major concern
• run data-intensive computations
in parallel on a large number of
commodity machines
→ need to rephrase algorithms
• our work: rephrase and scale-out the similarity-based
neighborhood methods on MapReduce
• proposed solution forms the core of the
distributed recommender of Apache Mahout
2

3. MapReduce
• popular paradigm for data-intensive parallel processing
– data is partitioned across the cluster in a distributed file system
– computation is moved to data
– fixed processing pipeline where user specifies two functions
– system handles distribution, execution, scheduling, failures etc.
3

4. cooccurrences
• start with a simplified view:
binary |U|x|I| matrix A holds interactions
between users U and of items I
• neighborhood methods share same
fundamental computational model
user-based item-based
• we focus on the item-based approach, its scale-out reduces to
finding an efficient way to compute the item similarity matrix
4

5. parallelizing S = ATA
• standard approach of computing item cooccurrences requires
random access to both users and items
foreach item i
not efficiently parallelizable
foreach user u who interacted with i
on partitioned data
foreach item j that u also interacted with
Sij = Sij + 1
• row outer product formulation of matrix multiplication
is efficiently parallelizable on a row-partitioned A
• each map invocation computes the outer product of a row of A,
emits the resulting matrix row-wise
• reducers sum these up to form S 5

6. parallel similarity computation
• real datasets not binary, either contain explicit feedback (ratings)
or implicit feedback (clicks, pageviews)
• algorithm computes dot products, these are not enough,
we want to use a variety of similarity measures (cosine, Jaccard
coefficient, Pearson correlation, ...)
• express similarity measures by 3 canonical functions, which can be
efficiently embedded into our algorithm
– preprocess adjusts an item rating vector
– norm computes a single number from the adjusted item rating vector
– similarity computes the similarity of two vectors from the norms and
their dot product
6

7. example: Jaccard coefficient
• preprocess binarizes the rating vectors
• norm computes the number of users that rated each item
• similarity finally computes the jaccard coefficient from the
norms and the dot product of the vectors
7

8. cost of the algorithm
• determined by the amount of data that has to be sent over the
network in the matrix multiplication step
• for each user, we have to process the square of the number of his
interactions → cost is dominated by the densest rows of A
• distribution of interactions per user is usually heavy tailed
→ small number of power users with an unproportionally high
amount of interactions drastically increase the runtime
• apply ‘interaction-cut’
– if a user has more than p interactions, only use a random sample of
size p of his interactions
– saw negligible effect on prediction quality for moderately sized p
8

9. scalability experiments
• cluster: Apache Hadoop on 6 machines (two 8-core Opteron CPUs, 32 GB
memory and four 1 TB drives each)
• dataset: R2 - Yahoo! Music (717M ratings, 1.8M users, 136k songs)
• similarity computation with differently sized interaction-cuts, measured
prediction quality on 18M held out ratings
9

10. scalability experiments
• ran several experiments in Amazon‘s EC2 cloud using up to 20 m1.xlarge
instances (15GB RAM, 8 virtual cores each)
→ linear speedup with the number of machines
→ linear scalability with a growing user base
10

11. thank you.
Questions?
Sebastian Schelter, Christoph Boden, Volker Markl
Database Systems and Information Management Group (DIMA), TU Berlin
mail: ssc@apache.org twitter: @sscdotopen
code to reproduce our experiments is available at:
https://github.com/dima-tuberlin/publications-ssnmm
The research leading to these results has received funding from the European Union (EU)
in the course of the project ‚ROBUST‘ (EU grant no. 257859) and used data provided by
‚Yahoo Academic Relations‘.
11