Downloaded 59 times
More Related Content
Cdma 101
- 1.
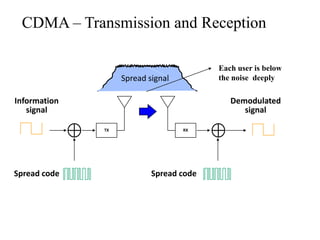
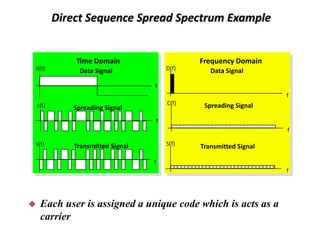
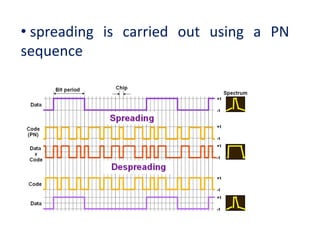
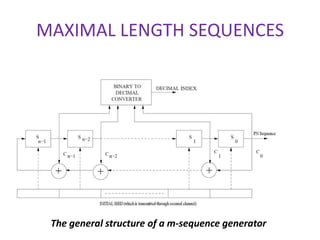
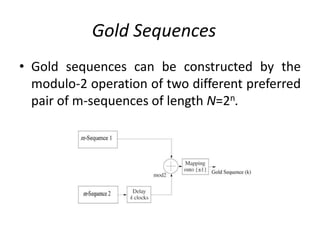
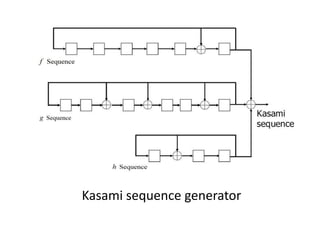
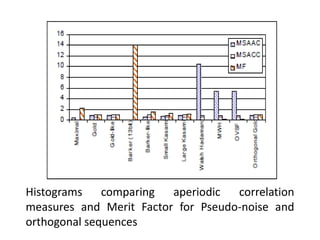
- 2. ANALYSIS OF DIFFERENTPSEUDORANDOM AND ORTHOGONAL SPREADING SEQUENCES IN DS-CDMA Mr.Praveen PN Lecturer ECE Department Safareena KK CEAKEEC101 S8 EC2
- 3. CDMA – Transmissionand Reception Each user is below the noise deeply Spread signal Information signal Demodulated signal TX Spread code RX Spread code
- 4. Direct Sequence SpreadSpectrum Example Time Domain d(t) Frequency Domain D(f) Data Signal Data Signal t f c(t) C(f) Spreading Signal Spreading Signal t f s(t) S(f) Transmitted Signal Transmitted Signal t f Each user is assigned a unique code which is acts as a carrier
- 5. INTRODUCTION • A devicein WCDMA system can access several services simultaneously • Spread spectrum is a radio communications system in which the baseband signal bandwidth is spread over a larger bandwidth by a higherfrequency signal. • CDMA (DS-CDMA) uses direct sequence spread spectrum (DSSS) technology to spread the spectrum
- 6. • spreading iscarried out using a PN sequence
- 7. PSEUDO-NOISE SEQUENCE • Apseudo-noise (PN) sequence is a sequence of 1’s and 0’s and it is periodic. • The PN sequences have the following three properties; Balance, run and auto-Correlation Properties.
- 8. MAXIMAL LENGTH SEQUENCES Thegeneral structure of a m-sequence generator
- 9. Gold Sequences • Goldsequences can be constructed by the modulo-2 operation of two different preferred pair of m-sequences of length N=2n.
- 10. • The setof Gold sequences generated with the two preferred pair of m-sequences f and h is defined as The auto correlation and cross correlation is given by
- 11. GOLD-LIKE SEQUENCES • Theseare similar to Gold sequence and have good correlation properties. • Gold-like sequence set contains 2n sequences and each sequence has a period of N = 2n-1. • Gold-like sequences can be defined as
- 12. BARKER SEQUENCES • Barkersequences are short length codes that offer good correlation properties. • A Barker code is a binary {-1, +1} sequence, {ci}, of some finite length N such that the discrete auto-correlation function r (τ), can be defined as: satisfies
- 13. KASAMI SEQUENCES • Ithas very low cross correlation • The degree n of the primitive polynomial used to generate Kasami sequences. • These sequences are defined for even values of n . • There are two types of kasami sequences a) small set of kasami sequences b) large set of kasami sequences
- 14.
- 15. ORTHOGONAL SEQUENCE • whenthe inner product between two sequences is zero then the signals are orthogonal ..ie •There are two types of orthogonal codes 1 Fixed length Orthogonal Codes 2 Variable length Orthogonal Codes
- 16. Fixed length orthogonalcode • Fixed length orthogonal codes include Walsh Hadamard (WH) and modified WH (MWH) codes. • The WH sequences of length N are defined with a class of orthogonal matrices HN called Hadamard matrices. • MWH codes are generated by multiplying the Hadamard matrix HN by a diagonal matrix DN of same order .
- 17. Variable length orthogonalcodes • Orthogonal codes with different length are called variable orthogonal code. • It also known as Orthogonal Spreading Factor (OVSF). Variable • The codes can be generated using the tree structure instead of Hadmard matrix.
- 18. ORTHOGONAL GOLD CODES •Orthogonal gold code can be constructed simply padding zero to the gold codes. by • Cross correlation value is zero • Length of orthogonal gold code is 2n • Auto correlation value is similar to that of gold sequence
- 19. MEAN SQUARE CORRELATION •The Mean Square Aperiodic Auto-Correlation (MSAAC) and Mean Square Aperiodic CrossCorrelation (MSACC) measures are accepted performance measures for correlation properties of sequences applied in DS-CDMA. • The mean square aperiodic auto-correlation (MSAAC) value RAC for a given code set containing M sequences is defined as:
- 20. • Measure forthe mean square aperiodic crosscorrelation (MSACC) value RCC is given by: • Auto-correlation refers to the degree of correspondence between a sequence. • Cross-correlation is the measure of agreement between two different codes.
- 21. MERIT FACTOR • Itis a criterion which quantitatively determine how significant the auto correlation degradation for a given set of sequences. • Sequences with low MF has narrow flat spectrum and they are neither suitable for CDMA • The Merit Factor for a sequence, ci(n), of length N having the auto-correlation function rij(τ ) is defined as:
- 22. • This isnothing more than the inverse of the MSAAC value for a given sequence.
- 23. RESULTS AND DISCUSSION •Performance of Gold code is good as compared to m-sequence. • The Barker sequences have many advantages over other PN sequences, but they are very limited in number of sequences • The autocorrelation and cross-correlation functions of Kasami sequences provide excellent properties, as good or better, than Gold Codes. Also, the possible numbers of large Kasami sequences are more compared to all other PN Sequences
- 24. Histograms comparing aperiodic correlation measures and MeritFactor for Pseudo-noise and orthogonal sequences
- 25. • The correlationvalues of orthogonal codes are high compared to that of PN sequences. But, compared to WH codes, the MWH codes have less correlation values making the crosscorrelation values of these codes high. • The orthogonal Gold codes have the correlation values similar to that of original Gold codes. • OVSF codes have the correlation functions, the MSAAC and MSACC values almost same as that of MWH codes
- 26. CONCLUSION • Large Kasamisequence has both good correlation values and high MF, which make these sequences to have wide flat spectrum that is better suited to be used in the WCDMA uplink transmission. • In the downlink of WCDMA, variable data rate is supported by using orthogonal variable spreading factor (OVSF) codes. • We have reviewed different PN as well as fixed- and variable-length orthogonal sequences that can be used in many applications including spreading codes for CDMA cellular networks.
- 27. REFERENCES • D.Torrieri, “PrinciplesOf Spread-Spectrum Communication Systems“, Springer, 2nd edition, 2011 •Valery P. Ipatov, “Spread Spectrum and CDMA Principles and Applications” Jhon Wiley & Sons Ltd, 2005. • K. Fazel and S. Kaiser, “Multi-carrier spreadspectrum: for future generation wireless systems”
- 28. Couch. L.W,“Digital and Analog Communication Systems”, 7thEd, Prentice Hall, Inc., 2007, T.S. Rappaport, “Wireless Communication, principles & practice”, PHI, 2001. E. STRO¨M, T. OTTOSSON, A.SVENSSON, “An Introduction to Spread Spectrum Systems”, Department of Signals and systems chalmers university of technology G¨oteborg, Sweden, 2002 .
- 29.