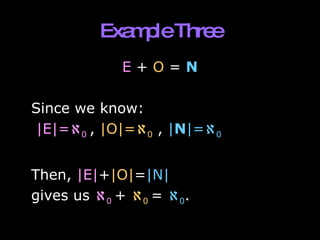The document defines cardinality as the number of elements in a set. It provides examples of finite sets and their cardinalities. It discusses bijective functions, equinumerous sets, cardinal and ordinal numbers. It defines countable, uncountable, denumerable, and finite sets. It proves that the set of real numbers is uncountable, and discusses the continuum hypothesis.

1. Cardinality Introduction to Analysis December 1, 2008 Samantha Wong

2. Cardinality Cardinality is the number of elements in a set. For Example: S = {1, 5, 8, 10}. Then this set contains four elements.

3. Some Definitions Two sets S and T are called equinumerous if there exists a bijective function from S onto T . We write S~T. The cardinal number of a set I n is n , and if S ~ I n , we say that S has n elements.

4. Notation We denote the cardinal number of a set S, as |S| . As in the previous example: S = {1, 5, 8, 10}. Then |S| = 4

5. Ordinal Numbers An ordinal number tells us the position of an element in a set. Going back to our example: S = {1, 5, 8, 10}. Then, 1 is the first ordinal 5 is the second ordinal 8 is the third ordinal 10 is the fourth ordinal.

6. Ordinal Numbers Second Third . . . Two Three . . . First One Ordinal Cardinal

7. Ordinal Numbers Example: A = {a, b, c}. a is the first element, b the second, c the third. So, we have three elements, and |A| = 3.

8. Some Definitions Finite : A set S is finite if S is equal to the empty set, or if there exists n an element of the natural numbers, and a bijection f :{1,2,…n}  S. Infinite : A set is infinite if it is not finite.

9. Some Definitions (cont’d) Denumerable :A set S is denumerable if there exists a bijection f : N  S. Countable : A set is countable if it is finite or denumerable. Uncountable : A set is uncountable if it is not countable.

10. A Bit of Cardinal Arithmetic Let s=|S|, and w=|W|. Then: s + w=|S|U|W|=|SUW| s x w = |S| x |W| = |S x W| s w = |S| |W| = |S W |

11. Cardinal Numbers Back to our example: S = {1, 5, 8, 10}. |S|=4. S is finite, because it has finitely many elements.

12. The Cardinality of Natural Numbers The set of natural numbers is not finite , but it is countable . | N | =  0

13. Example One The cardinality of the natural numbers and even natural numbers is the same. Let E = even natural numbers. Let N = natural numbers. Bijection f : N  E , where f(n)=2n. Then E has the same cardinality as N. | E | =  0 = | N |

14. Example Two The cardinality of the odd natural numbers and the even natural numbers are the same. Let O = odd natural numbers. Bijection f : O  E , where f(n) = n+1. Then O has the same cardinality as E (and N). |O| = |E| =  0 = | N |

15. Example Three E + O = N Since we know: |E|=  0 , |O|=  0 , | N |=  0 Then, |E| + |O| = |N| gives us  0 +  0 =  0 .

16. Definition Power set : Given any set S , let P(S) denote the collection of subsets of S . Then P(S) is called the power set of S . For example: Let S = {1,2}. Then, P(S) = {  , {1},{2},{1,2}}. *Note that |S| < |P(S)|

17. Theorem For any set S, |S| < |P(S)|.

18. Theorem Any subset of a countable set is countable.

19. The Cardinality of Real Numbers Theorem: The set of real numbers is uncountable . We denote the cardinality of the real numbers as: | R | = C

20. The Real Numbers are Uncountable (Proof) Proving the real numbers are uncountable. Assume that R is countable. Construct a number that is not in the set. By constructing a number not in our original set, we conclude that R is uncountable.

21. The Real Numbers are Uncountable (Proof) Assume that the set of real numbers is countable. Then any subset of the real numbers is countable (by the previous theorem). So let us look at the set S = (0,1)

22. The Real Numbers are Uncountable (Proof) Since we have defined S to be countable, we can list all elements of S . So S = { s 1 , s 2 , … , s n }

23. The Real Numbers are Uncountable (Proof) so we can write any element of S in its decimal expansion. Meaning, s 1 = 0. a 11 a 12 a 13 a 14 … s 2 = 0. a 21 a 22 a 23 a 24 … and so on. And each a ij is an element of {0,1, 2, 3, 4, 5, 6, 7, 8, 9}.

24. The Real Numbers are Uncountable (Proof) Let y = 0. b 1 b 2 b 3 b 4 … Where: b i = {1, if a nn ≠ 1; 8 if a nn = 1}.

25. The Real Numbers are Uncountable (Proof) For example, if x 1 = 0. 3 2045…. x 2 = 0.4 4 246… x 3 = 0.57 1 24… Then y = 0. 1 1 8 …

26. The Real Numbers are Uncountable (Proof) y is made up of 1’s and 8’s, so y is in S = (1,0) But, y ≠ s n because it differs from s n at the nth decimal place. S must be uncountable. Then the real numbers are uncountable.

27. Recall… Since the real numbers are uncountable, and the natural numbers are countable: |N| < |R|  0 < C There are more real numbers than natural numbers!

28. Hmm…  0 < ? < C

29. The Continuum Hypothesis Cantor believed his sequence, 0, 1, 2, …,  0 ,  1 ,  2 , …,   contained every cardinal number. But, which one is C?  0 is the number of finite ordinal numbers.  1 is the number of ordinal numbers that are either finite or in the  0 class. And so on…

30. The Continuum Hypothesis (cont’d) There are exactly C = 2  0 real numbers and C >  0 . But, does C =  1 ? Cantor believed so.

31. The Generalized Continuum Hypothesis  α +1 = 2  α for all α ?

32. The Continuum Hypothesis  0 < ? < C l Georg Cantor suggested that no such set exists . Kurt Godel showed that this couldn’t be disproved . Paul Cohen showed that this couldn’t be proved either. 1900 1940 1963

33. End