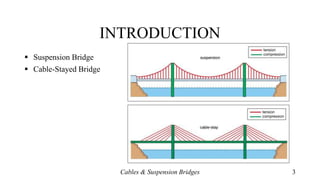
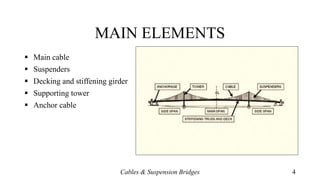
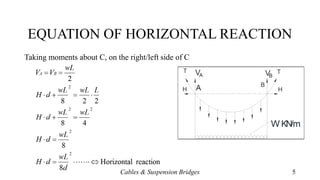
This document discusses the key elements and design considerations of cable-stayed and suspension bridges. It covers: - The main components of these bridges, including main cables, suspenders, decking, towers, and anchor cables. - Equations for calculating horizontal reactions, cable tension at various points, and the parabolic shape of loaded cables. - Methods for determining the total cable length and anchoring cables to the ground via guide pulleys or saddle arrangements on piers. - The use of a three-hinged stiffening girder to support the bridge deck between cable supports.

1. Cables & Suspension Bridges 1
CABLES & SUSPENSION
BRIDGES

2. CONTENTS
 Introduction
 Main elements
 Equation of horizontal reaction
 Cable tension at ends
 Shape of the loaded cord
 Length of the cable
 Anchor cables
 Suspension brigde with three-hinged stiffening girder
Cables & Suspension Bridges 2

3. INTRODUCTION
 Suspension Bridge
 Cable-Stayed Bridge
Cables & Suspension Bridges 3

4. MAIN ELEMENTS
 Main cable
 Suspenders
 Decking and stiffening girder
 Supporting tower
 Anchor cable
Cables & Suspension Bridges 4

5. EQUATION OF HORIZONTAL REACTION
Taking moments about C, on the right/left side of C
Cables & Suspension Bridges 5

6. CABLE TENSION AT ENDS
The cable tension T at any end is the resultant of vertical and horizontal reaction at
the end.
Cables & Suspension Bridges 6

7. CABLE TENSION AT ENDS
Cables & Suspension Bridges 7
T= Tension at any point p of the cable
Ɵ=Inclination of the tangent at p with horizontal consider equilibrium of part PB
 Resolving the forces on this part horizontally.
 Minimum tension in cable will occur at c
cosTH 
HTT c  min

8. CABLE TENSION AT ENDS
 Maximum tension in cable will occur at ends
 The inclination β of T with vertical is given by,
Cables & Suspension Bridges 8
2
2
max
16
1
2 d
LwL
T 
d
LwL
d
wL
42
/
8V
H
tan
2


9. SHAPE OF THE LOADED CORD
 Under the uniformly distributed load the cable takes the from of a parabola
 The equation of cable , with either support as origin will be,
Cables & Suspension Bridges 9
)(
4
2
xLx
L
d
y 

10. LENGTH OF THE CABLE
The equation for total length of the cable is given by,
Cables & Suspension Bridges 10
.
3
8 2
l
h
lL 

11. ANCHOR CABLES
The main cables attach to the ends of the deck, rather than to the ground via large
anchorages. The design is well-suited for construction a top elevated piers, or in
areas of unstable soils where anchorages would be difficult to construct.
There are generally two arrangement used:
1. The suspension cable can be passed over the guide pulley for anchoring it to
the other side
2. The suspension cable and anchor cable can be attached to a saddle mounted on
rollers.
Cables & Suspension Bridges 11

12. ANCHOR CABLES
Cables & Suspension Bridges 12
Cable passed over guide pulley at
the support
Cable clamped to saddle carried on
smooth rollers on top of pier

13. CABLE PASSED OVER GUIDE PULLEY
In case of guide pulley arrangement, the suspension cable passes over the guide pulley,
=Inclination of the suspension cable with vertical
=Inclination of the anchor cable with vertical
Vertical pressure on top of pier,
Horizontal pressure on top of pier,
Cables & Suspension Bridges 13
1
2
 21 coscos  TVp
 21 sinsin  THp

14. CABLE CLAMPED TO SADDLE CARRIED
ON SMOOTH ROLLERS
In case of saddle on roller arrangement, rollers do not have any horizontal reaction.
Therefore, the horizontal components of the tensions in the suspension cable and the
anchor cable will be equal.
The vertical pressure on the top of the pier is,
Cables & Suspension Bridges 14
HTT  2211 sinsin 
2211 coscos  TTVp 

15. SUSPENSION BRIGDE WITH THREE-
HINGED STIFFENING GIRDER
Cables & Suspension Bridges 15

16. 16