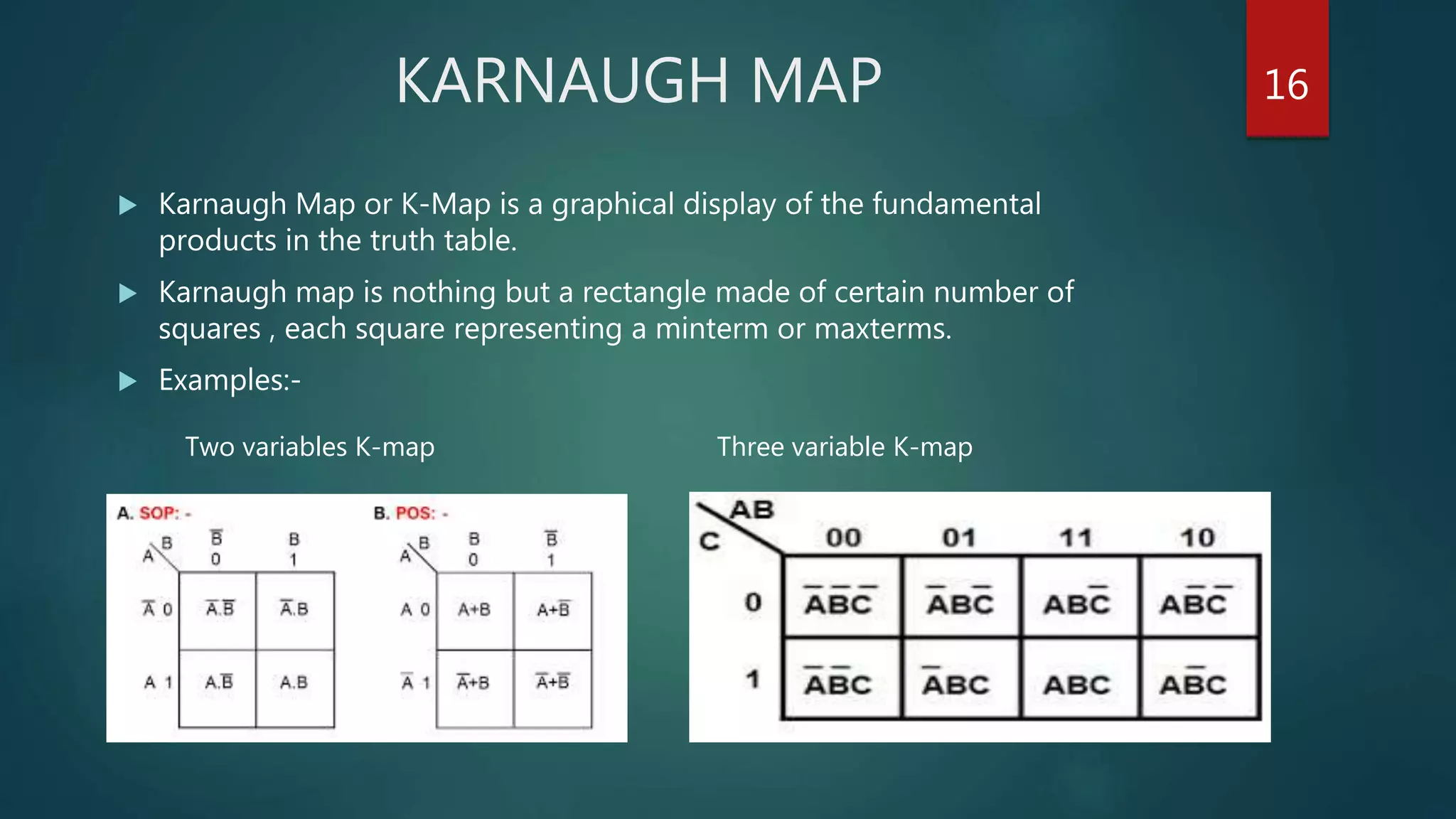
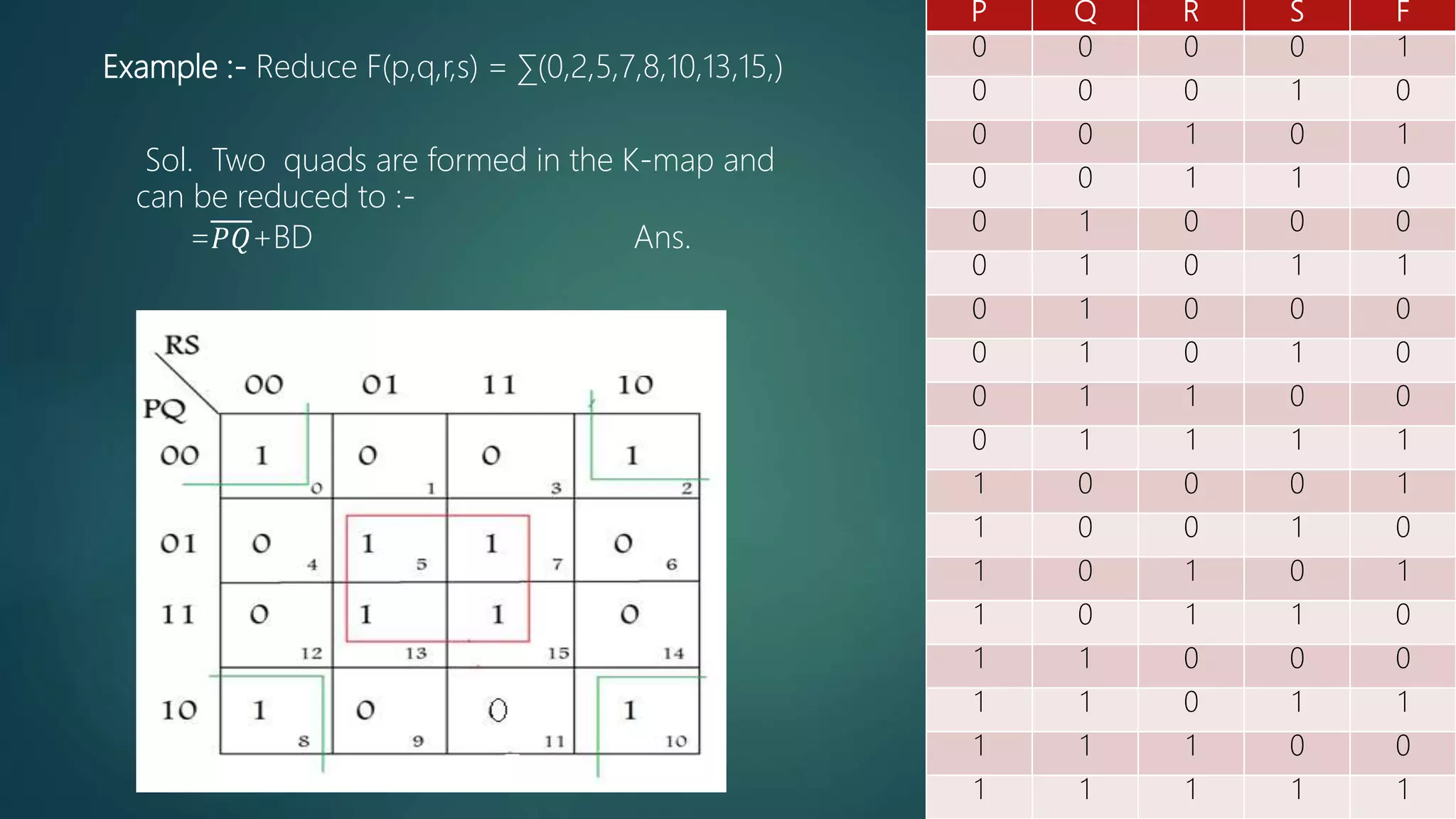
The document summarizes a seminar presentation on Boolean algebra. The presentation covered the development of Boolean algebra, logical operators like NOT, OR, AND, logic gates, derivation of Boolean expressions, canonical expressions, and methods for minimizing Boolean expressions including algebraic methods and Karnaugh maps. It provided examples to illustrate different concepts like logical operators, logic gates, canonical expressions, Karnaugh maps, and minimizing expressions.

1. Subject seminar
on Boolean algebra
PRESENTED By:-
Shivanshu dixit
GUIDED BY :-
Mrs. NAMRITA GUPTA
1

2. Development of Boolean algebra
 Long ago, Aristotle constructed a complete system of former
logic.
 He also wrote six books on the system of former logic problems.
 For centuries afterward, mathematicians kept trying solving the
logic problems.
 But only George Boole was able to arrive at a solution for his own
system of logic in 1854 called it BOOLEAN ALGEBRA.
 In 1938, Claude E. Shannon applied BOOLEAN ALGEBRA to solve
relay logic problems.
2

3. LOGICAL OPERATORS
3

4. NOT Operator :-
 This operator operates on the single variable .
 The operation performed is known as complementation.
 The symbol is ¯ (bar) and X’s complement is represented as 𝑋.
X 𝑋
X 𝑿
0 1
1 0
VENN DIAGRAM TRUTH TABLE
4

5. OR Operator :-
 Or operator donates logical addition .
 The symbol + represents Or operation.
 So, X+Y can be read as X OR Y,
X Y
X Y X+Y
0 0 0
0 1 1
1 0 1
1 1 1
5

6. AND Operator :-
 AND operator performs logical multiplication.
 The symbol for AND operator is . (dot).
 So, X.Y is read is X AND Y.
x YX
.
Y
X Y X.Y
0 0 0
0 1 0
1 0 0
1 1 1
6

7. LOGIC GATES
 A gate is a basic electronic circuit which operates on one or more signal to produce an
output.
 Gates are digital (two- state) circuits because the input or output signal are either low
voltage (denotes 0) or high voltage
(denotes 1).
 Gates are often called logic circuits because they can be analysed by Boolean algebra.
 There are three basic logic gates :-
o Inverter (Not gate)
o OR gate
o And gate
7

8. INVERTER(NOT Gate)
 It has only one input signal and one output signal.
 The output state is always opposite to the input state.
 An inverter is also known as NOT gate because output is not same as the
input.
X 𝑿
0 1
1 0
SYMBOL
X 𝑋
8

9. OR Gate
 The OR gate has two or more input signal but only one output signal.
 If any one input signal is 1 (high) the out put signal is 1 (high).
 If all inputs are 0 (low) then the output is also 0 (low).
 An OR gate can have as many inputs as desired.
A B Q
0 0 0
0 1 1
1 0 1
1 1 1
9

10. AND Gate
 The AND gate has two or more input signal and produce one output
signal.
 When all inputs are1 (high) then the output is 1 ,otherwise the output is 0.
 An AND gate can have as many input as desired.
A B Q
0 0 0
0 1 0
1 0 0
1 1 1
10

11. Derivation of Boolean expression
 Boolean expressions which consist of a single variable or its complement
e.g., X or Y or 𝑍 are known as literals .
 MINTERMS :-
 A minterm is a product of all literals within the logic system.
 If value of a variable is 0, then its complement is multiplied else the variable
itself is multiplied.
 Example :- if X=1,Y=0,Z=1 then the minterm is X𝑌Z.
 MAXTERMS:-
 A maxterm is the sum of all literals within the logic system.
 If value of a variable is 1, then its complement is added else the variable itself is
added.
 Example :- if X=1,Y=0,Z=1 then the minterm is 𝑋+Y+𝑍.
11

12.  Convert X+Y into minterms.
Sol. X+Y=X.1+Y.1
= X.(Y+𝑌)+Y.(X+𝑋)
= XY+X𝑌+XY+𝑋Y
= XY+X𝑌+𝑋Y
 Convert X.Y into maxterms.
Sol. X.Y=(X+0).(Y+0)
= (X+Y.𝑌).(Y+X.𝑋)
= (X+Y)(X+𝑌)(X+Y)(𝑋+Y)
= (X+Y)(X+𝑌)(X+Y)(𝑋+Y)
Let us solve some problems :-
12

13. Canonical Expression
 Boolean Expression composed entirely either of minterms or of Maxterms is referred to
as Canonical Expression.
 Canonical expression can be represented in the following two terms :-
 Sum-of-Products (S-O-P) :-
• When a BOOLEAN expression is represented purely as sum of minterms it is said
to be in canonical Sum-Of-Product.
• Example ;- XY+XZ+ZY
 Product-Of-Sum (P-OS) ;-
• When a BOOLEAN expression is represented purely as sum of maxterms it is said
to be in canonical Product-Of-Sum (P-OS) .
• Example ;- (X+Y).(Y+Z).(X+Z)
13

14. MINIMIZATION OF BOOLEAN
EXPRESSION
 After obtaining an S-O-P or P-O-S expression the next thing is to simplify
the Boolean expression.
 And then the expression is implemented using logic gates.
 And a minimized Boolean expression means less no of logic gates which
means simplified circuitary.
 There are many ways of simplification of Boolean expressions, some are :-
 Algebraic method
 Using Karnaugh Maps
 Quine-Mccluskey Method
14

15. Algebraic Method
 This method makes use of Boolean postulates, rules and theorems to
simplify the expressions.
 Example:- Simplify 𝑋𝑌+𝑋+XY.
Sol. 𝑋𝑌+𝑋+XY
= (𝑋 + 𝑌)+𝑋 + XY
= 𝑋+𝑌+XY
= (X+𝑋)(𝑋+Y)+𝑌
= 𝑋+Y +𝑌
= 𝑋+1
= 1
15

16. KARNAUGH MAP
 Karnaugh Map or K-Map is a graphical display of the fundamental
products in the truth table.
 Karnaugh map is nothing but a rectangle made of certain number of
squares , each square representing a minterm or maxterms.
 Examples:-
Two variables K-map Three variable K-map
16

17. How to map in K-map ?
 First draw the K-map as per the given number of variables.
 Now look for the output 1 (S-O-P) or 0 (P-O-S) and mark in the squares.
 The next step is reduction ,can be done by making groups as :-
 Pair Reduction :- Remove the variable which changes its state from complemented to
uncomplemented or vice versa ,removes one variable.
 Quad Reduction :- Remove the two variables which changes their states.
 Octet Reduction :- Remove the three variables which changes their states.
 Map Rolling :- Map rolling means roll the map i.e., consider the map as if its left edges are
touching its right edges and top edges are touching the bottom edges .
17

18. Example :- Reduce F(p,q,r,s) = ∑(0,2,5,7,8,10,13,15,)
P Q R S F
0 0 0 0 1
0 0 0 1 0
0 0 1 0 1
0 0 1 1 0
0 1 0 0 0
0 1 0 1 1
0 1 0 0 0
0 1 0 1 0
0 1 1 0 0
0 1 1 1 1
1 0 0 0 1
1 0 0 1 0
1 0 1 0 1
1 0 1 1 0
1 1 0 0 0
1 1 0 1 1
1 1 1 0 0
1 1 1 1 1
Sol. Two quads are formed in the K-map and
can be reduced to :-
=𝑃𝑄+BD Ans.

19. Thank You
19