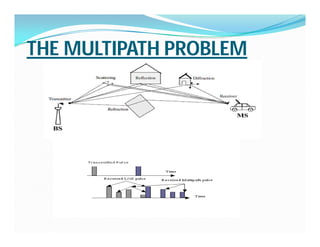
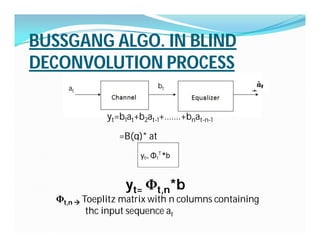
The document discusses blind equalization within wireless communication, detailing the multipath problem, fading characteristics, and the significance of equalization to reverse signal distortion. It compares adaptive equalizers, which require training sequences, with blind equalizers that infer the transmitted signal from the received signal using statistical methods, such as the Bussgang theorem. Additionally, it addresses challenges in designing equalizers and iterative deconvolution processes while exploring strategies to enhance performance and reduce resource waste.

1. BLIND EQUALIZATION:
ASPECTS OF COMMUNICATION

2. OUTLINE
 Wireless Channel
 The Multipath Problem
Fading Characteristics
Basic Idea of Equalization
Role of Equalization
Challenges in designing Channel Equalizer
Shortcomings of non-adaptive Equalizer
The Adaptive Equalizer
Operation of Adaptive Equalizer
Basics of Blind Deconvolution
The Bussgang Theorem
Bussgang Algorithm in Blind deconvolution
Assumptions in applying Bussgang Algorithm
Iterative Deconvolution process
Convolution Noise
Non-convexity of cost function
Advantages & Disadvantages
heading to next development

3. WIRELESS CHANNEL
Received
Information

4. THE MULTIPATH PROBLEM

5. FADING CHARACTERISTICS

6. Basic Idea of Equalization
•In telecommunication, the equalizer is a device that attempts
to reverse the distortion incurred by a signal transmitted
through a channel.
• Heq(f) = 1/H(f)
• Goal is to mitigate the effects of ISI due to system behavior,
multipath fading & attenuation.
• The thumb rule: If
Coherence Time(Tc)> Symbol Duration(Tm) --
Equalization is mandatory

7. Role of Equalization

8. Challenges to design Equalizer
 Equalizing process to mitigate ISI effect sometimes
enhance the noise power (shortcoming of the ZF
equalizer)
 Introduction of MMSE Equalizer Introduction of
cost function  Derivation of Wiener-Hoff equations

9. Shortcomings of Non-adaptive
equalizers
 Since in wireless channels are time varying in
nature, non-adaptive equalizers can only perform
well for a very limited period of time
 Periodically estimation the channel and
update of the equalizer coefficients accordingly
are required in real-time commercial
communication system leading to training &
tracking modes of adaptive equalizers

10. THE ADAPTIVE EQUALIZERS
2 modes of operation:
(a)Training Mode
(b)Tracking Mode

11. Operation of Adaptive Filters:-
 The standard adaptive approach, though attractive
in handling time-variant channels, has to waste a
fraction of the transmission time for a training
sequence.
 Even the so-called decision feedback equalization
(DFE), which does not explicitly use a training
sequence, requires sending known training
sequences periodically to avoid catastrophic error
propagation

12. Operation of Adaptive Filters(contd.)
The GSM Frame Structure
Nearly 17% resource is wasted in sending the
training bits to configure the equalizers which
is not cost-effective.
A special equalization process is needed
where the use of “training bits” are avoided
causing efficient use of channel- vision to
“BLIND EQUALIZATION”

13. BASICS OF BLIND EQUALIZATION
 Blind equalization is a digital signal processing technique in
which the transmitted signal is inferred (equalized) from
the received signal, while making use only of the transmitted
signal statistics. Hence, the use of the word blind in the name
 Both the channel model & Transmitted signal is to be
determined by observing the received signal characteristics.
 The concept of Unsupervised learning
 Use of higher order statistics- BUSSGANG STATISTICS

14. THE BUSSGANG THEOREM
 A theorem of Stochastic analysis
 Statement: The cross-correlation of a Gaussian signal
before and after it has passed through a nonlinear
operation are equal up to a constant
It was first published by Julian J. Bussgang in 1952 while he
was at the Massachusetts Institute of Technology

15. Illustration…
 Let {X(t)} be a zero-mean stationary Gaussian random
process and {Y(t)}=g(X(t)) where g(.) is a nonlinear
amplitude distortion
If is the autocorrelation function of X(t) , then
the cross-correlation function of X & Y is:
where C is a constant that depends only on g(.)

16. BUSSGANG ALGO. IN BLIND
DECONVOLUTION PROCESS
at
bt
yt=b1at+b2at-1+…….+bnat-n-1
=B(q)* at
yt= Φt,n*b
Φt,n  Toeplitz matrix with n columns containing
thc input sequence at

17. Necessary Assumptions for
Bussgang Algorithm
 The data sequence x(n) is white; i.e. data symbols are
i.i.d random variable with zero mean & unit variance:
E[x(n)]=0
And
E[x(n)x(k)]=1, k=n
=0, k n
 The pdf of x(n) is to be uniformly distributed as follows:

18. Iterative deconvolution Process
**Governing Equations

19. The Convolution Noise
Convolutional Noise
Basic block diagram of the Blind equalizer

20. Non-convexity of Cost Function
The Error performance surface of the Iterative
deconvolution process may have local minima in
addition to a global minima
 Non-convergence form of the Cost function results in
Ill-Convergence

21. Advantages & Disadvantages
.

22. HEADING TO NEXT DEVELOPMENT:-
 To overcome the problems, explicit algorithms
using cyclostationary statistics through
tricepstrum calculation is developed where no
minimization of cost function is required though
computational complexity increases.

23. References
1. Adaptive Filter Theory by S. Haykin, PHI
2. Wireless Communications, Andrea Goldsmith, Stanford University
3. Adaptive Filters: Theory & Applications, B.Farhang-Boroujeny, Wiley
4. Wireless Communication: Principles & Practice, T.S. Rappaport, Pearson
5. Adaptive Filtering Primer with MATLAB, A.D. Poularikas & Z.M.Ramadan, CRC
Publication
6. Blind Identification and Equalization Based on Second-Order Statistics: A Time
Domain Approach, Lang Tong, Member, IEEE, Guanghan Xu, Member, IEEE, and
Thomas Kailath, Fellow, IEEE
7. BLIND DECONVOLUTION BY MODIFIED BUSSGANG ALGORITHM, Sirnone Fiori,
Aurelio Uncini, and Francesco Piaua, Dept. Electronics and Automatics - University of
Ancona (Italy)
8. Least Squares Approach to Blind Channel Equalization, Kutluyl Dogancay, Member,
IEEE, and Rodney A. Kennedy, Member, IEEE
9. Blind Equalization by Direct Examination of the Input Sequences, Fredric Gustafsson,
Member, IEEE, and Bo Wahlberg, Member, IEEE
10. Self-Recovering Equalization and Carrier Tracking in Two-Dimensional Data
Communication Systems, DOMINIQUE N. GODARD, MEMBER, IEEE