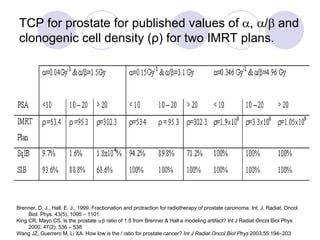
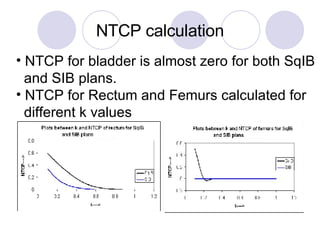
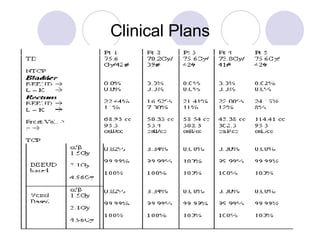
The document discusses calculating tumor control probability (TCP) and normal tissue complication probability (NTCP) for intensity-modulated radiation therapy (IMRT) plans using the biologically effective equivalent uniform dose (BEEUD) concept. TCP and NTCP values were calculated for sample IMRT plans using the BEEUD methodology and compared to other methods. The BEEUD concept was able to calculate TCP similarly to voxel-based methods and provides an advantage for pre-treatment plan evaluation, though it may produce different NTCP values than the L-K model.

1. Concept of Biologically Effective Equivalent Uniform Dose to compute Tumor Control Probability and Normal Tissue Complication Probability for IMRT Plans. T. S. KEHWAR , D.Sc., Ph.D. M. Saiful Huq, PhD and Dwight E. Heron, MD University of Pittsburgh Cancer Institute UPMC Cancer Centers, Pittsburgh

2. BEEUD concept is the radiation biological dose which produces equivalent biological effect to that of a uniform radiation dose. Using BEEUD methodology TCP and NTCP values were calculated for IMRT plans generated by Eclipse (sample case) and ADAC Pinnacle (Clinical cases) planning systems. Comparison of the results from BEEUD concept and other methods were made to determine the efficacy of the concept. OBJECTIVES

3. TV is divided into n number of sub-volumes (voxels) and assumed that each voxel has uniform dose distribution. Voxel based TCP for TV is given by TCP =  i TCP i = exp[ -   i v i exp( -  BED ti )] (1) BEEUD for Tumors Tumor with non-uniform dose distribution SANCHEZ-NIETO, B & NAHUM, AE. THE DELTA-TCP CONCEPT: A CLINICALLY USEFUL MEASURE OF TUMOR CONTROL PROBABILITY. Int. J. Radiation Oncology Biol. Phys., Vol. 44, No. 2, pp. 369–380, 1999

4. TCP for TV is given by TCP = exp[ -  V exp( -  BEEUD t )] (2) From Eqs. (1) & (2), we have derived BEEUD t = - (1/  ) ln[(1/V)  i v i exp( -  BED ti )] (3) Tumor with uniform dose distribution

5. BEEUD for normal tissues NTCP equation of LQ model is NTCP = exp[– N 0 v – k exp(–  BED n )] (4)

6. Organ/normal tissue close to TV have very high dose gradient. Organ volume is divided into ‘ n ’ small voxels of infinitasimal volumes and assumed that each voxel has uniform dose disribution. Tumor Normal tissue/organ D ref

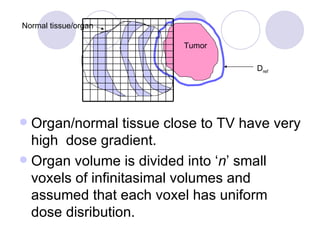
7. One of the limitation of NTCP concept (Eq.4) that it can not calculate net NTCP using voxel by voxel method, because it’s not an additive term of volume. Additive form of volume is given by NTCP Factor NTCPF i = exp[(N 0 ) -1/k (V i /V 0 ) exp{(  /k) BED ni }] (5) Sum of voxel based NTCPF for entire organ / normal tissue volume NTCPF = exp[(N 0 ) -1/k  i {(V i /V 0 ) exp[(  /k) BED ni ]}] (6) BEEUD for normal tissues

8. For BEEUD n NTCPF is given by NTCPF = exp[(N 0 ) -1/k (V 0 /V 0 )exp{(  /k) BEEUD n }] or NTCPF = exp[(N 0 ) -1/k exp{(  /k) BEEUD n }] (7) Eqs. (6) & (7) gives BEEUD n = (k/  ) ln[  i {(V i /V 0 ) exp[(  /k) BED i ]}] (8) And NTCP for whole organ may be written as NTCP = exp[– N 0 exp(–  BEEUD n )] (9) Normal tissue with Uniform dose distribution

9. Two IMRT plans generated for a sample cases PTV1 = prostate + seminal vesicles+1.0 cm, PTV2 =prostate + 0.75 cm. SqIB plan: 54Gy/27Fx to PTV1 followed a boost of 24Gy/12Fx to PTV2. SIB plan: 54Gy/27Fx to PTV1 and 78Gy/27Fx to PTV2. Maximum dose limits of 50Gy for bladder and femurs, 45Gy for rectum, priority of 80% and limiting volume to 10% . dDVH of both IMRT plans were used to calculate BEEUDs to compute TCP and NTCP. RESULTS AND DISCUSSION

10. TCP for prostate for published values of  ,  /  and clonogenic cell density (ρ) for two IMRT plans. Brenner, D. J., Hall, E. J., 1999. Fractionation and protraction for radiotherapy of prostate carcinoma. Int. J. Radiat. Oncol. Biol. Phys. 43(5), 1095 – 1101. King CR, Mayo CS. Is the prostate  ratio of 1.5 from Brenner & Hall a modeling artifact? Int J Radiat Oncol Biol Phys 2000; 47(2): 536 – 538. Wang JZ, Guerrero M, Li XA. How low is the / ratio for prostate cancer? Int J Radiat Oncol Biol Phys 2003;55:194–203

11. NTCP calculation NTCP for bladder is almost zero for both SqIB and SIB plans. NTCP for Rectum and Femurs calculated for different k values

12. Clinical Plans

13. CONCLUSIONS BEEUD n based on LQ model so have radiobiological reminifications. BEEUD method calculates same TCP as voxel based TCP method. However different NTCP from L – K model. BEEUD method has the advantage for pre-evaluation of the plans.

14. Thanking you all