The document discusses the necessity of evaluating the uncertainty of measurement (UM) in medical testing, highlighting both analytical and non-analytical components, particularly the role of biological variation. It outlines methods for calculating combined uncertainties, emphasizing the importance of accurately interpreting test results in clinical contexts. Additionally, the document presents examples and guidelines for integrating biological variability into the assessment of uncertainty, underscoring its impact on clinical decision-making.

1. Use of Biological
Variation as an
Uncertainty
Component
Evaluation Methods of Uncertainty of
Measurement for Medical Testing
https://consultglp.com
by
Yeoh Guan Huah
GLP Consulting, Singapore

2. Outline
• A review of the uncertainty of measurement
(UM) calculation methods by component-by-
component approach
• Necessity to consider non-analytical
uncertainty components in addition to the
analytical uncertainty in the laboratory
• Biological variation – what and why
• How to incorporate biological variation in the
overall evaluation of UM.

3. Introduction
• The ultimate use of analysis data with its
associated uncertainty of measurement (UM)
must be fit for intended purpose
• Data generated by medical laboratory are used
for any signaling which may differentiate health
from disease, based on some pre-set reference
ranges for diagnostic decision
• Amongst other applications, these data are also
adopted for clinical monitoring of a patient upon
treatment.

4. Introduction
• Both ISO 15189 and ISO/IEC 17025 accreditation standards
have given uncertainty of measurement a new
perspective.
• They have recognized that apart from the analytical
uncertainty during the testing process, there are other
non-analytical uncertainty components to be considered
as well.
• For industrial, environmental and commodity testing,
ISO/IEC 17025 stresses the importance of taking
representative samples from the lot (population) for
analysis. Hence, sampling uncertainty is incorporated as
another uncertainty contributor, if applicable.
• For clinical application of a test result, the in vivo biological
variability of the measurand as an uncertainty component
cannot be ignored for clinical interpretation.

5. Reported result with uncertainty : X + U (units)
• Measurement uncertainty U is expressed
as:
• Test result : X + U
• and, U = k x u
• where k is a coverage factor (usually k = 2 or
1.96 for 95% confidence), and
• u, the combined standard uncertainty
expressed as standard deviation
• U is also called expanded uncertainty,
assumed rightly a normal probability
distribution of data
5
Example:
Consider an expression for a
measurand (urea in serum):
“5.0 + 0.2 mmol/L with 95%
confidence”
The + 0.2 mmol/L is the
uncertainty ( U ) of the supposed
5.0 mmol/L serum urea
measurement.
Its combined standard
uncertainty (u ) therefore, is
0.2/2 or 0.1 mmol/L

6. Basic methods for combining uncertainty
components
• Calculated from a sum and/or a difference of independent
measurements with associated standard uncertainties
• Let: R = X + Y or R = X – Y
• Then, (uR)2 = (uX)2 + (uY)2
• where uR , uX and uY are the respective analytical
standard uncertainty (as standard deviation)
• Therefore, combined standard uncertainty uR = (uR)2
• Note: X and Y are of same units and involved in addition
& subtraction conditions

7. Worked example No. 1
• Anion gap (AG) is calculated based on the results of serum (plasma)
ions: sodium, potassium, chloride and bicarbonate, in the form:
• AG = (Na+ + K+) – (Cl- + HCO3-)
Ion,
mmol/L Test result
Standard
deviation, u
Na+ 140 1.2
K+ 3.9 0.1
Cl- 102 1.3
HCO3- 24 1.2
Therefore,
AG = (140+3.9) – (102 + 24) = 17.9 mmol/L
𝐶𝑜𝑚𝑏𝑖𝑛𝑒𝑑 𝑆𝐷 𝑅= (1.2)2+(0.1)2+(1.3)2+(1.2)2
= 2.1 mmol/L
Report:
Anion Gap (AG) = 18 + 4 mmol/L
with a coverage factor of 2 (95% confidence)

8. Basic methods for combining uncertainty components
• From multiplication and/or division of independent measurements
• Using the Propagation Law of Standard Deviation,
• Let:
𝑢(𝑦)2 =
𝑖=1
𝑛
𝜕𝑓
𝜕𝑥𝑖
2
𝑢(𝑥𝑖)2
• R =
𝑃×𝑉
𝑇
with standard
deviations uP , uV , uT , then,
• 𝑐 𝑃 =
𝜕𝑅
𝜕𝑃
=
𝑉
𝑇
• 𝑐 𝑉 =
𝜕𝑅
𝜕𝑉
=
𝑃
𝑇
• 𝑐 𝑇 =
𝜕𝑅
𝜕𝑇
= −
𝑃×𝑉
𝑇2
𝑢 𝑅
2 = 𝑐 𝑃
2
𝑢 𝑃
2 + 𝑐 𝑉
2
𝑢 𝑉
2 + 𝑐 𝑇
2
𝑢 𝑇
2
= (
𝑉
𝑇
)2 𝑢 𝑃
2 + (
𝑃
𝑇
)2 𝑢 𝑉
2 + (−
𝑃𝑉
𝑇2)2 𝑢 𝑇
2
Dividing both sides by 𝑅2 = (
𝑃×𝑉
𝑇
)2 gives:
(
𝑢 𝑅
𝑅
)2
= (
𝑢 𝑃
𝑃
)2
+ (
𝑢 𝑉
𝑉
)2
+ (
𝑢 𝑇
𝑇
)2
, or
𝑢 𝑅
𝑅
= (
𝑢 𝑃
𝑃
)2+ (
𝑢 𝑉
𝑉
)2 + (
𝑢 𝑇
𝑇
)2
𝒊. 𝒆. , 𝑪𝑽 𝑹 = 𝑪𝑽 𝑷
𝟐
+ 𝑪𝑽 𝑽
𝟐
+ 𝑪𝑽 𝑻
𝟐

9. Worked example No. 2
• In a creatinine clearance test, the following calculation applies:
• C = (U x V ) / (P x T )
Parameter Unit Value u
U mmol/L 10.0 0.25
V ml 1500 15
P mmol/L 0.1 0.01
T secs 86400 0
By calculation,
C = (10.0 mmol/L x 1500 ml)/(0.1 mmol/L x 24 hrs x 3600 sec)
= 1.74 ml/sec
and,
(
𝑢 𝑅
1.74
)2
=(
0.25
𝑈10.0
)2
+(
15
1500
)2
+(
0.01
0.1
)2
+(
0
86400
)2
= 0.0107
Therefore,
uR = 1.74 x 0.0107 = 0.18 ml/sec
Report:
Creatinine clearance C = 1.74 + 0.36 ml/sec with the
coverage Factor of 2 for 95% confidence

10. Non-analytical uncertainty contributors
• In medical testing, there are many
potential uncertainty contributors
which can significantly affect test
results, apart from the analytical
process itself, such as:
• Improper practice during specimen
collection
• Poor specimen handling during transit
to the laboratory
• Patient related factors like biological
variability and the presence of any drug
residues

11. Analytical uncertainty component
• The laboratory’s analytical quality comes from two factors for total
analytical error as its analytical goal:
• Intermediate precision (random error; imprecision)
• Analytical bias (systematic error)
• Intermediate precision or imprecision (ua) is estimated from its
long-term combined (pooled) standard deviation after a series of
analysis in replicates by different analysts within the laboratory on
different occasions on a stable internal quality control serum
sample.
• Analytical bias is evaluated by studying any significant difference
between the average test result against the target or certified value
of the internal QC sample through the Student’s t-test. If there is a
significance difference between the mean result and the certified
value, then the standard uncertainty of bias (ub) is estimated.

12. Why do we consider the biological variation?
• There are many clinical uses of the test results reported.
• As a test result must be ‘fit for purpose’, there is a need to assess its clinical
goal in addition to the analytical goal.
• For some measurands, an analytical goal may not be physiologically or clinically
relevant. Then, the method imprecision study would be sufficient.
• However most medical laboratory need to identify if UM information when
reported could significantly affect clinical interpretations and patient
management.
• Hence, there is a necessity to have additional non-analytical uncertainty
component in the overall estimation of UM to set such goal.
• This additional uncertainty component is the intra-individual biological
variation of the measurand.

13. Components of biological variation (BV)
• Actually, there are two types of components of biological
variation, namely:
• Intra-individual (random fluctuation of analytes around the
setting point of each individual), sometimes termed as “within-
subject” BV;
• Inter-individual (overall variation from the different person’s
setting point), sometimes termed as “between-subject” BV.
• The laboratory’s analytical method, instrument and
reagents do not make difference in BV estimates.

14. Some applications of biological variation
 Evaluating the clinical significance of changes in consecutive test
results from an individual in monitoring treatment progress
 Setting quality specifications for analytical performance (usually
targeting the analytical goal as a percentage of BV) to satisfy the
general needs of diagnosis and monitoring
 Validating new procedures in a laboratory
 Assessing the usefulness of population-based reference values
 Determining which type of specimen (e.g. plasma, serum, 24-hr
urine, first-morning urine) is optimal for analyzing a specific
constituent

15. Relationship of analytical imprecision and biological
variation
• There are 3 levels of analytical goal for long-term imprecision
(CVa) based on intra-individual biological variation (CVi):
• Optimum: CVa < 0.25 x CVi
• Desirable: CVa < 0.50 x CVi
• Minimum: CVa < 0.75 x CVi
• For analytes with unavailable CVi data, other criteria may be
used, such as relative performance in inter-laboratory
comparison studies or proficiency testing programs, certified
reference interval, professional clinical opinion, etc.

16. Relationship of analytical imprecision and biological
variation
• If test results are interpreted using reference or clinical decision
values determined by a different method, bias should be considered
as a component of uncertainty to be estimated.
• The inter-individual biological variation CVg is to be incorporated.
• Like imprecision, we have to ensure the three levels of analytical
goal for bias (CVb) based on biological variation are met:
• Optimum:
• Desirable:
• Minimum:
𝐶𝑉𝑏 ≤ 0.125 × 𝐶𝑉𝑖
2
+ 𝐶𝑉𝑔
2
𝐶𝑉𝑏 ≤ 0.250 × 𝐶𝑉𝑖
2
+ 𝐶𝑉𝑔
2
𝐶𝑉𝑏 ≤ 0.375 × 𝐶𝑉𝑖
2
+ 𝐶𝑉𝑔
2

17. Biological variation database
• There are study findings which indicate that the factors
inherent to the subject, such as sex, age, race,
geographical location, do not produce changes in BV
results
• Practically all the currently available estimates of
biological variation (more than 300 analytes) have been
compiled in a database:
https://www.westgard.com/biodatabase1.htm
• The intra-individual (or within-subject) coefficients of
variation (in %) from the database can be used to
evaluate the clinical significance of changes in two
consecutive results from a patient, in addition to the
analytical variation.

20. Summation of analytical uncertainty &
biological variation
• If the combined estimate of coefficient of variation of
reported test result (CVT) covers both the CV of analytical
imprecision (CVa) and that of within-subject biological
variation (CVi) for a comparison of two consecutive test
results from a patient, we then have:
• CVT
2 = CVa
2 + CVi
2
• Note: If test results are clinically interpreted by comparison
with reference or previous values produced by the same
analytical method, analytical bias component is not required.

21. Worked example No. 3
• Plasma alkaline phosphatase (ALP) activity for a patient:
• 1st day’s result : 95 U/L; 3rd day’s result : 108 U/L
• UM for ALP : CVa = 1.45% at QC sample mean : 87 U/L
• ALP intro-individual BV (given by Westgard website): CVi = 6.45%
• Were these two sets of daily test results of any significant
different?
• Sum of analytical & BV as CV’s:
• CVT = (CVa
2 + CVi
2) = (1.452 + 6.452) = 6.61%

22. Worked example No. 3 (contd.)
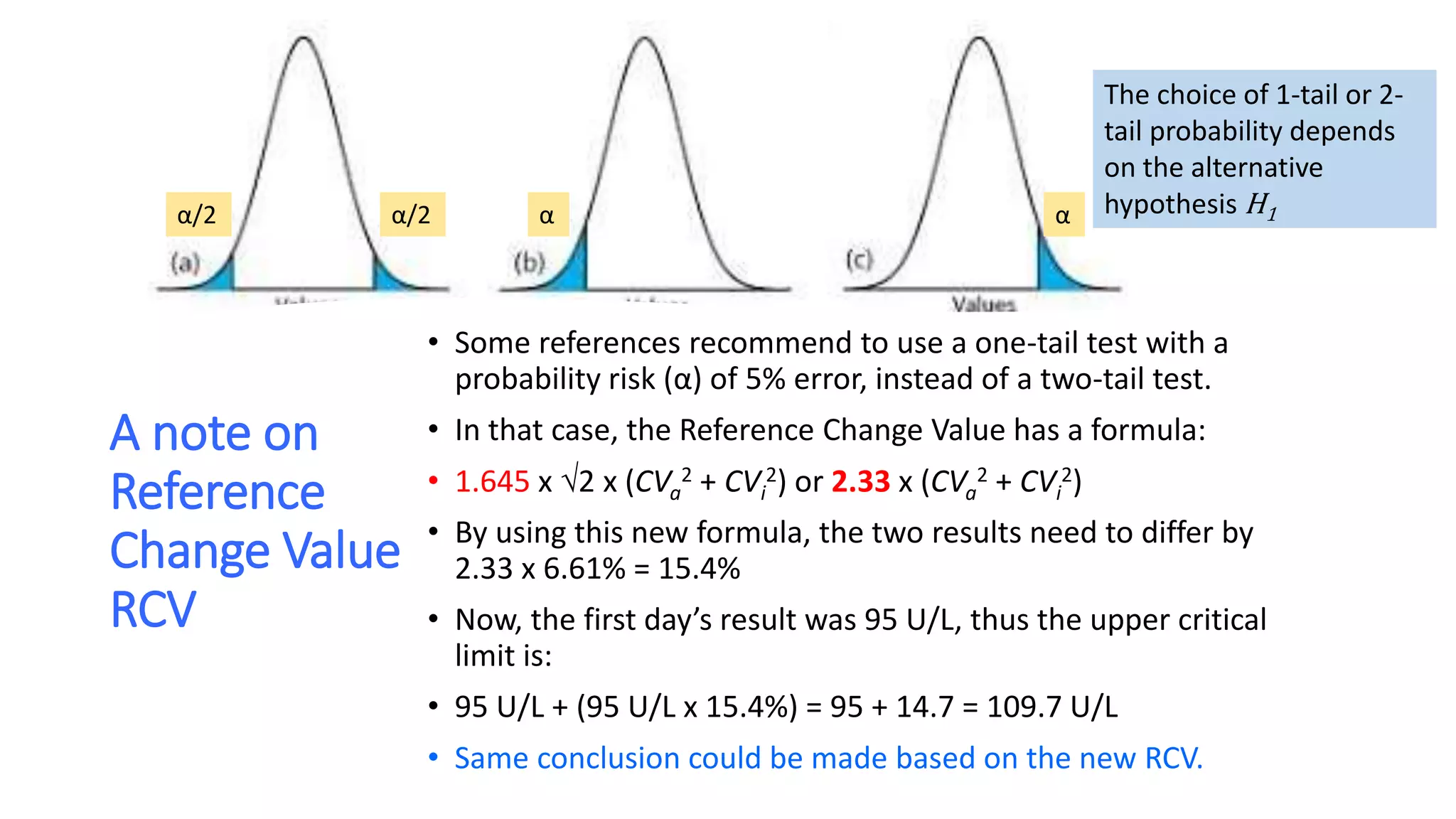
• If the two test results are analytically and biologically different, the “critical difference”
or Reference Change Value (RCV) is to be:
• 1.96 x 2 x (CVa
2 + CVi
2) or 2.77 x (CVa
2 + CVi
2) for 95% confidence
• That means the two results need to differ by 2.77 x 6.61% = 18.3%
• Now, the first day’s result was 95 U/L, thus
• 95 U/L + (95 U/L x 18.3%) = 95 + 17.4 = 112 U/L
• and, 95 U/L - (95 U/L x 18.3%) = 95 - 17.4 = 77.6 U/L
• So, the critical range of expanded uncertainty is [77.6 U/L, 112 U/L]
• The second result would have to be at least 112 U/L for there to be 95% confidence that
it was both analytically and biologically different from the first result. We can therefore
conclude that the test results of 95 U/L and 108 U/L are analytically different, but
probably not biologically different.

23. A note on
Reference
Change Value
RCV
• Some references recommend to use a one-tail test with a
probability risk (α) of 5% error, instead of a two-tail test.
• In that case, the Reference Change Value has a formula:
• 1.645 x 2 x (CVa
2 + CVi
2) or 2.33 x (CVa
2 + CVi
2)
• By using this new formula, the two results need to differ by
2.33 x 6.61% = 15.4%
• Now, the first day’s result was 95 U/L, thus the upper critical
limit is:
• 95 U/L + (95 U/L x 15.4%) = 95 + 14.7 = 109.7 U/L
• Same conclusion could be made based on the new RCV.
ααα/2α/2
The choice of 1-tail or 2-
tail probability depends
on the alternative
hypothesis H1

24. How do we get the factor 1.96 x 2 or 1.645 x 2?
• A measurement result, X, is associated with a standard deviation +sX
• The duplicate result, Y, on the same sample is also associated with the
same standard deviation +sX
• When an average value is calculated for X and Y, we have a total
variance of
• sX
2 + sX
2 = 2sX
2
• Therefore, the pooled standard deviation is 2 x sX
• The choice of coverage factor k = 1.96 or 1.645 depend on either 2-tail
or 1-tail hypothesis testing, assuming a normal distribution with an
error probability α = 0.05 or 95% confidence.

25. Conclusion
• It is a good practice to maintain a list of measurands with their
respective RCV (reference change value) to define healthy and
non-healthy situations.
• Remember that the RCV is applied for the target analyte in each
pair of consecutive results from the same patient
• The laboratory information system (LIMS) can be set to flag off
the second report with a predefined signal after the numeric
result of the target analyte is keyed in.
• Most important challenge for the medical personnel is how to
explain the UM concept to requesting doctors in a clinically
meaningful way.

26. References
• “Uncertainty of Measurement in Quantitative
Medical Testing – A Laboratory Implementation
Guide” by Australasian Association of Clinical
Biochemists, November 2004
• “Application of Biological Variation – A Review” by
Ricos C. et al, Biochemia Medica 2009, 19(3):250-9
• “Desirable Biological Variation Database
specifications” by James Westgard,
https://www.westgard.com/biodatabase1.htm