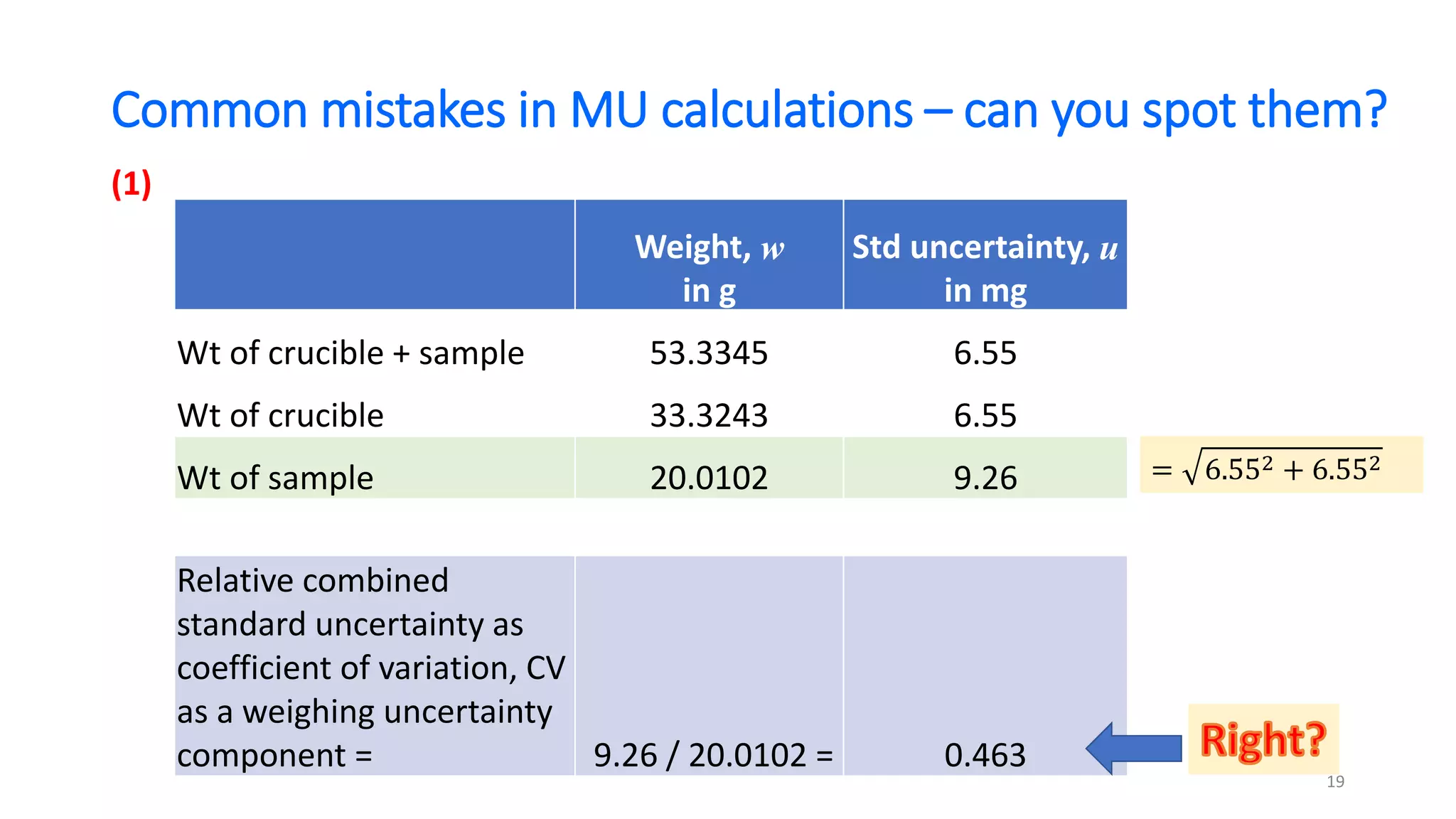
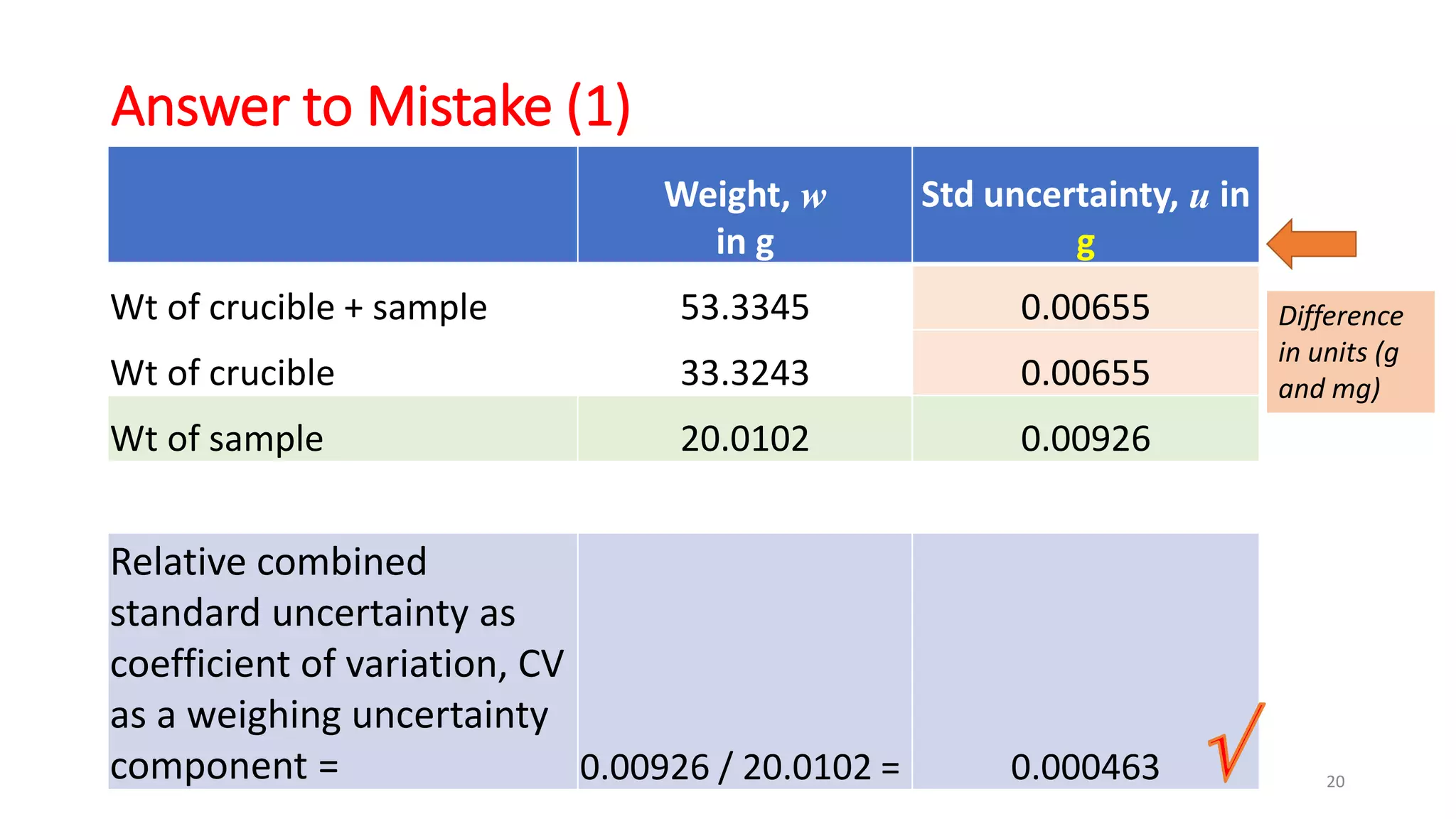
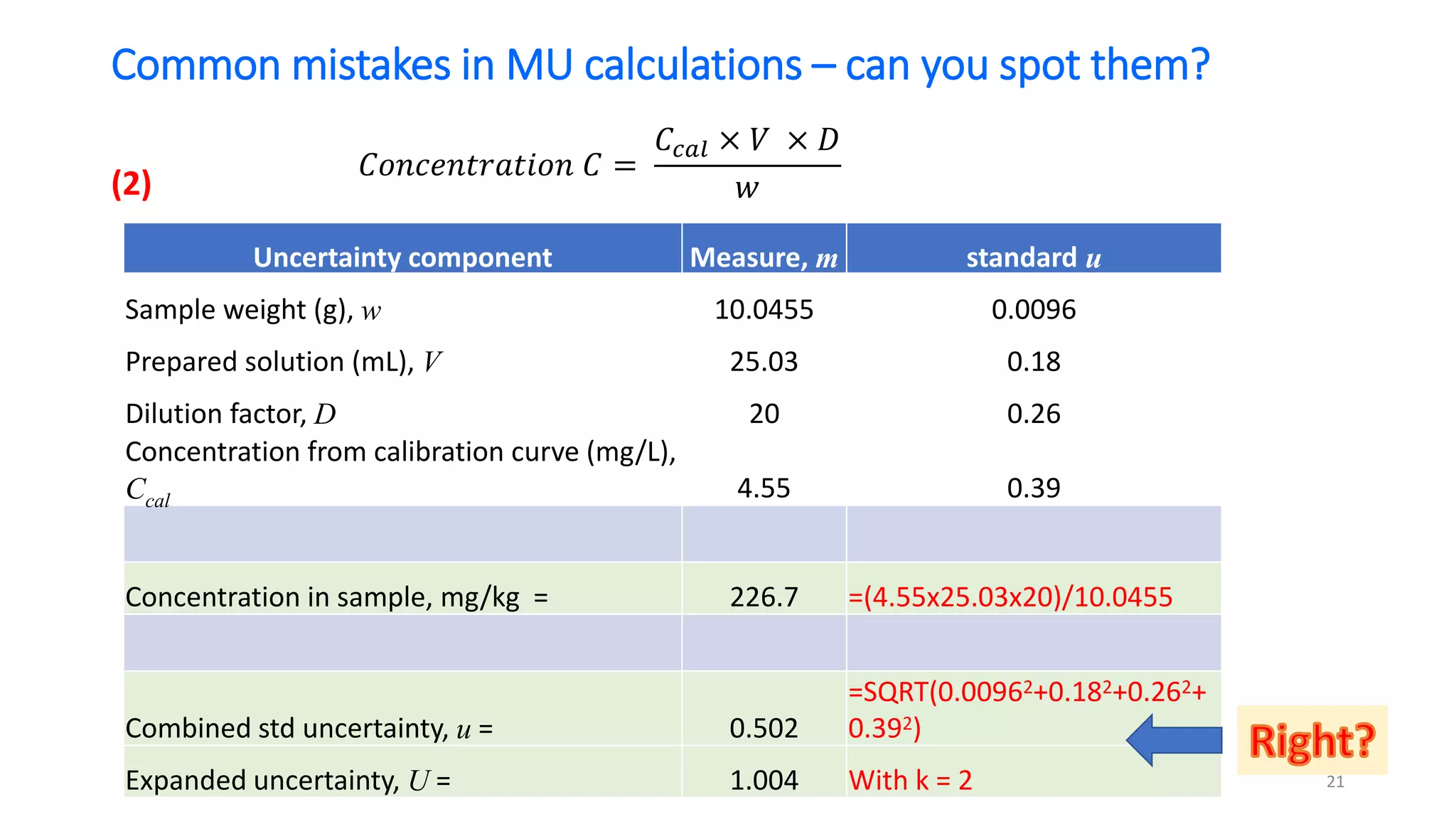
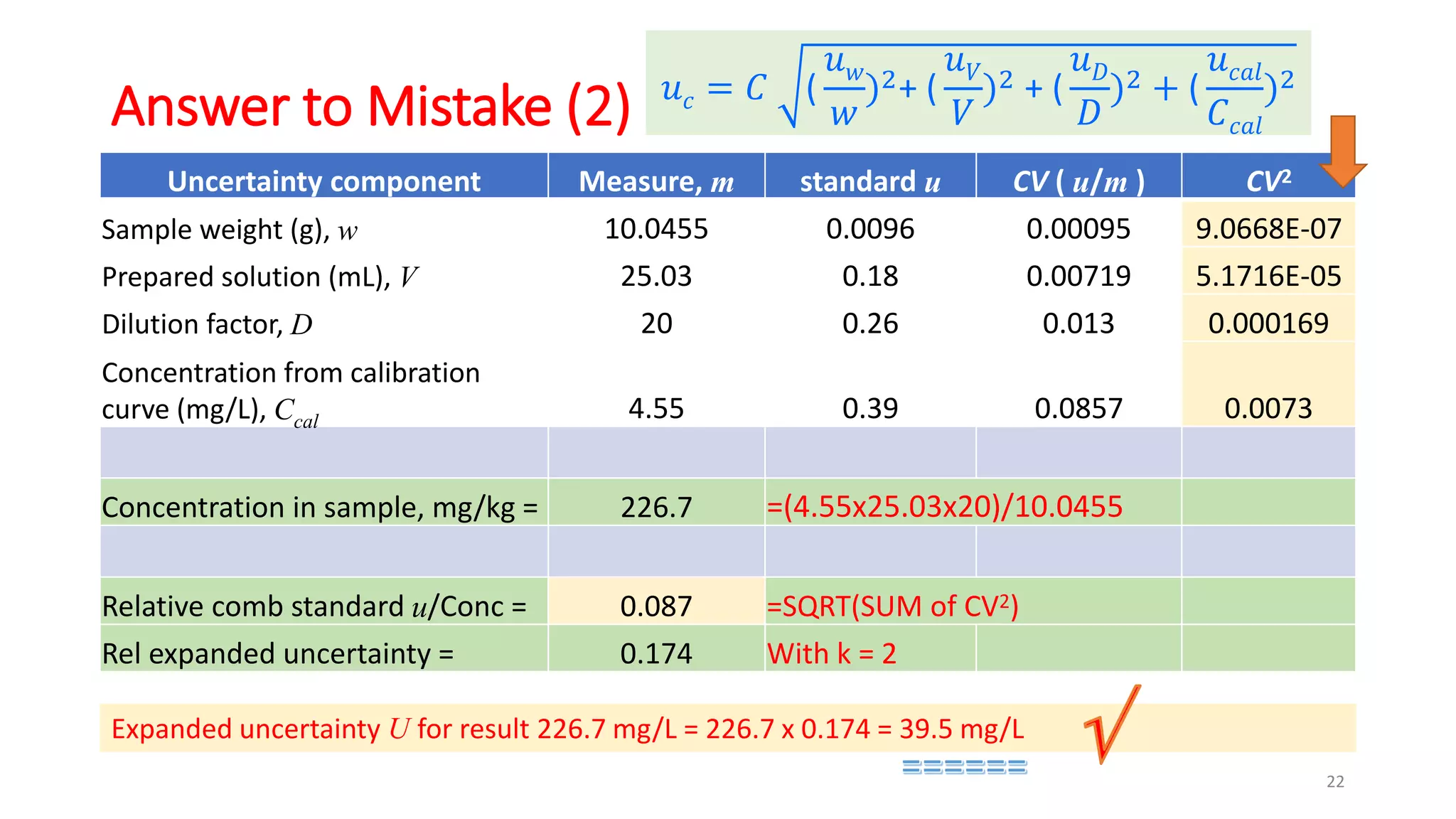
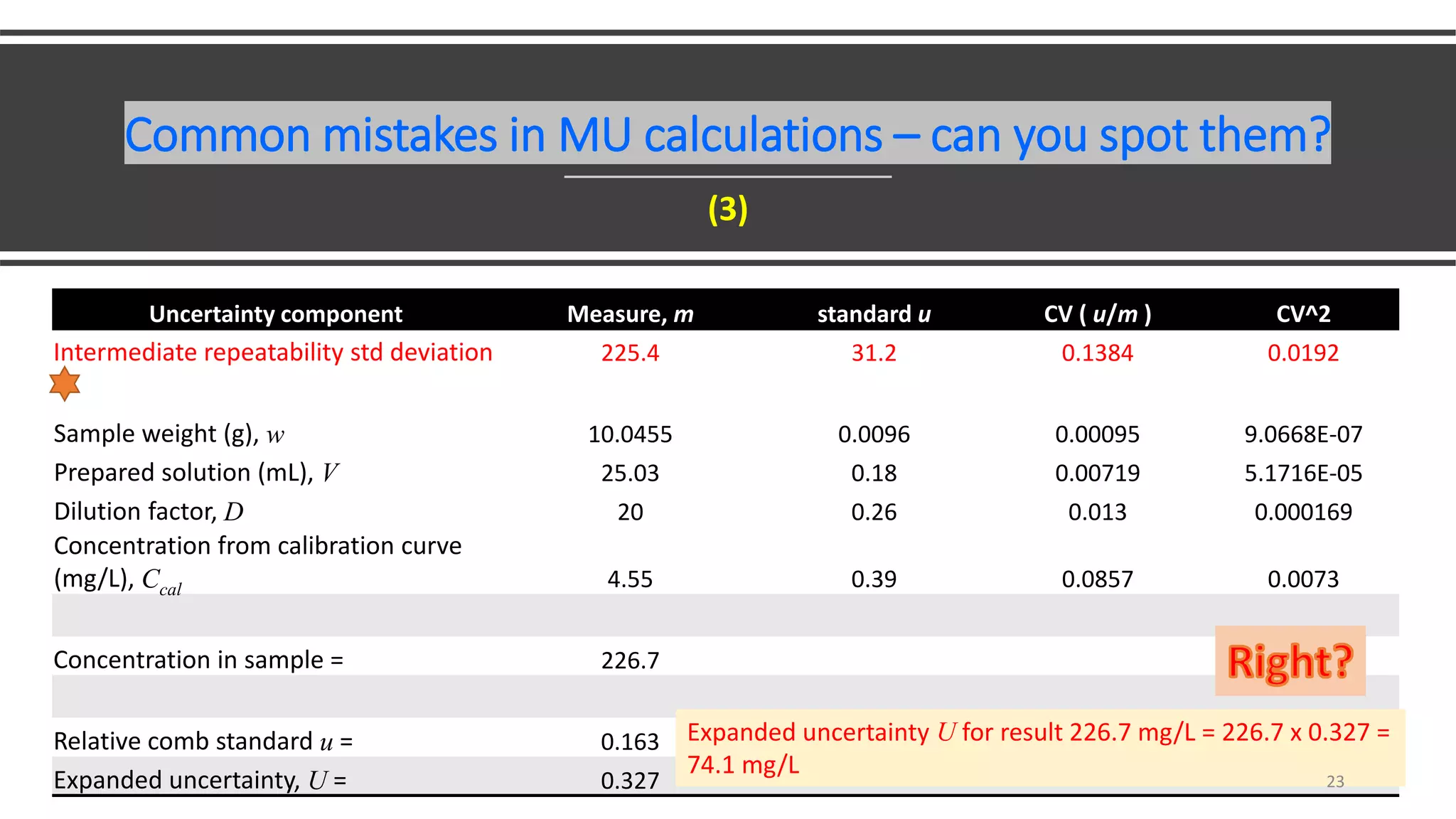
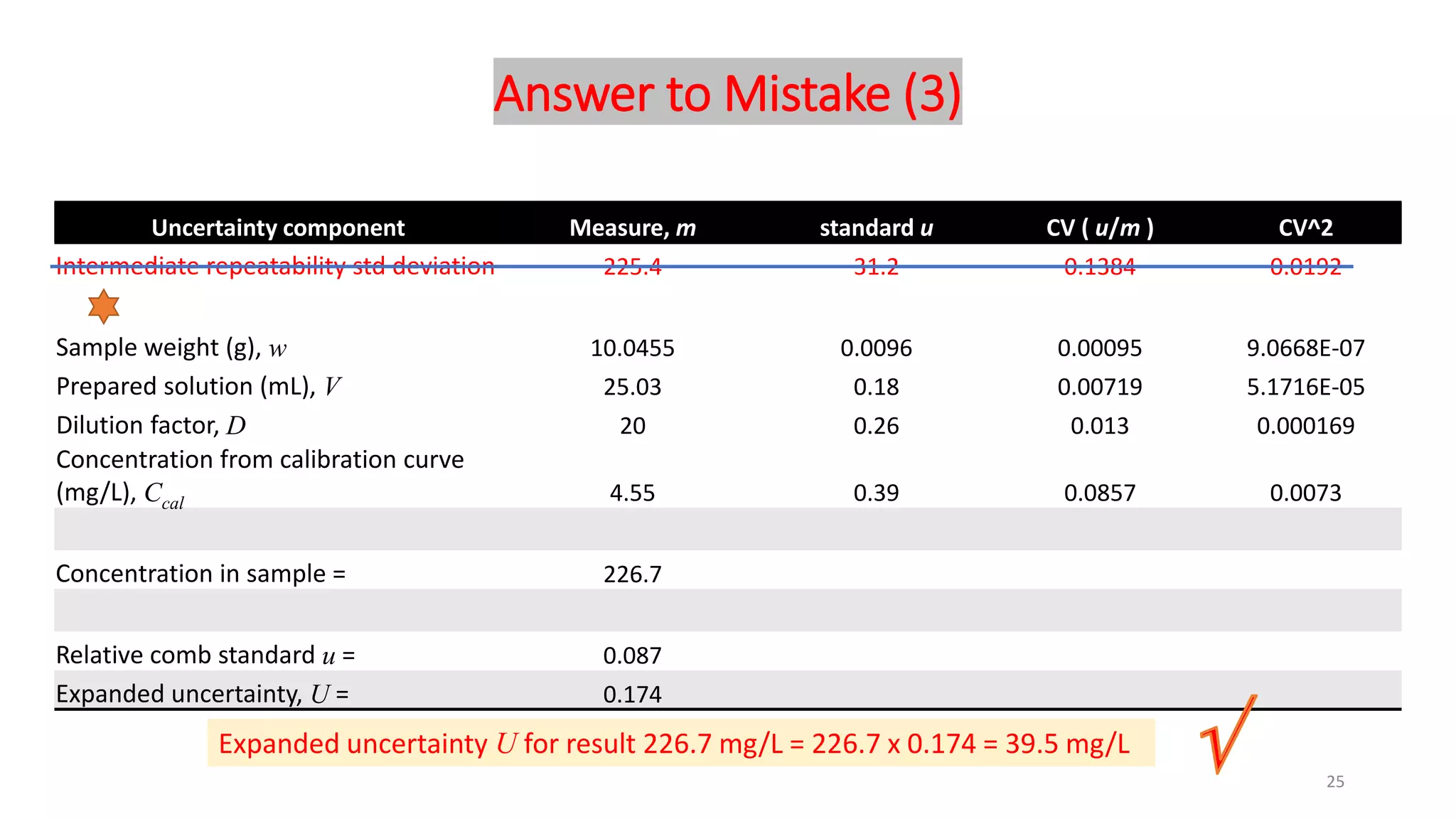
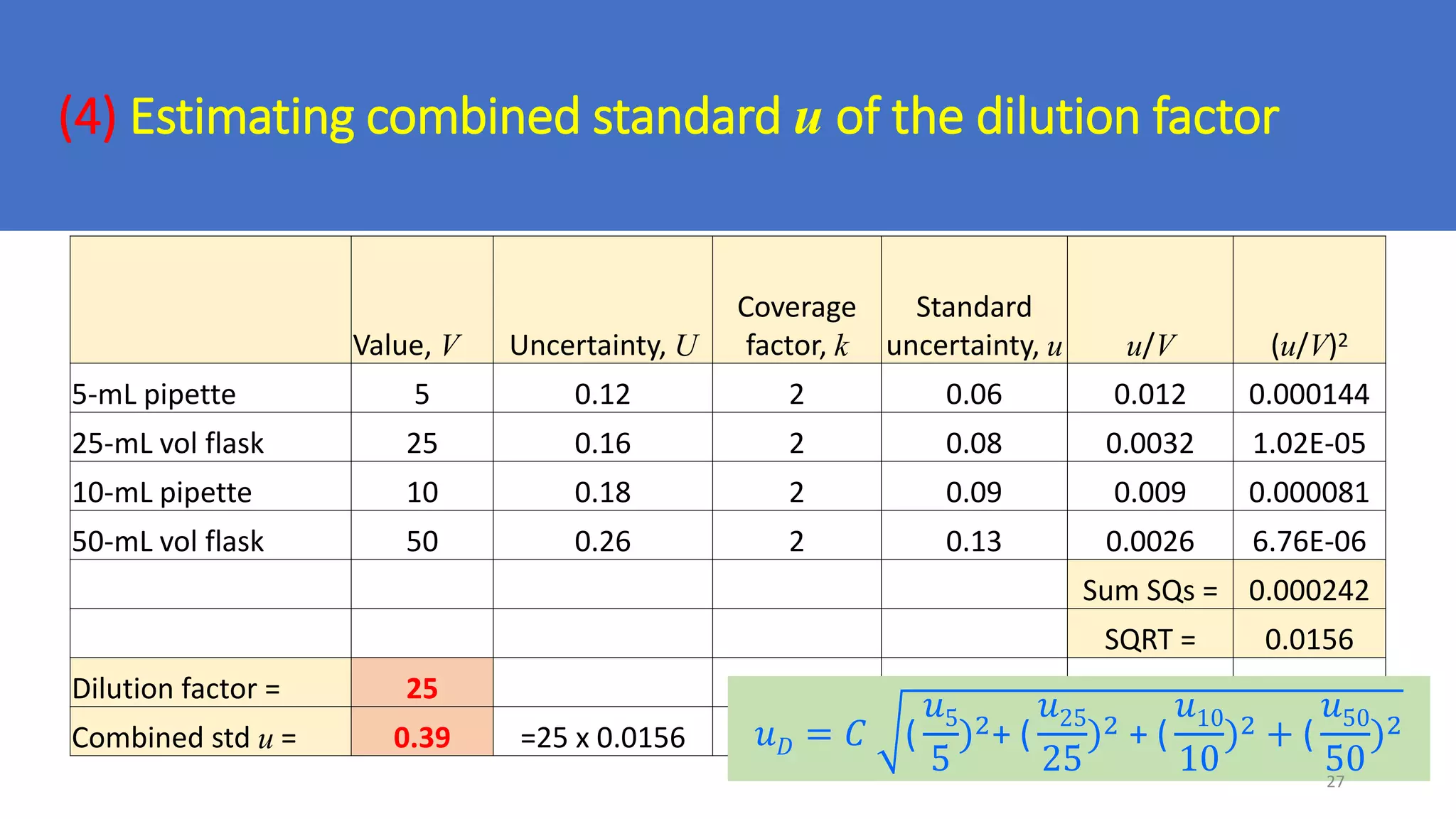
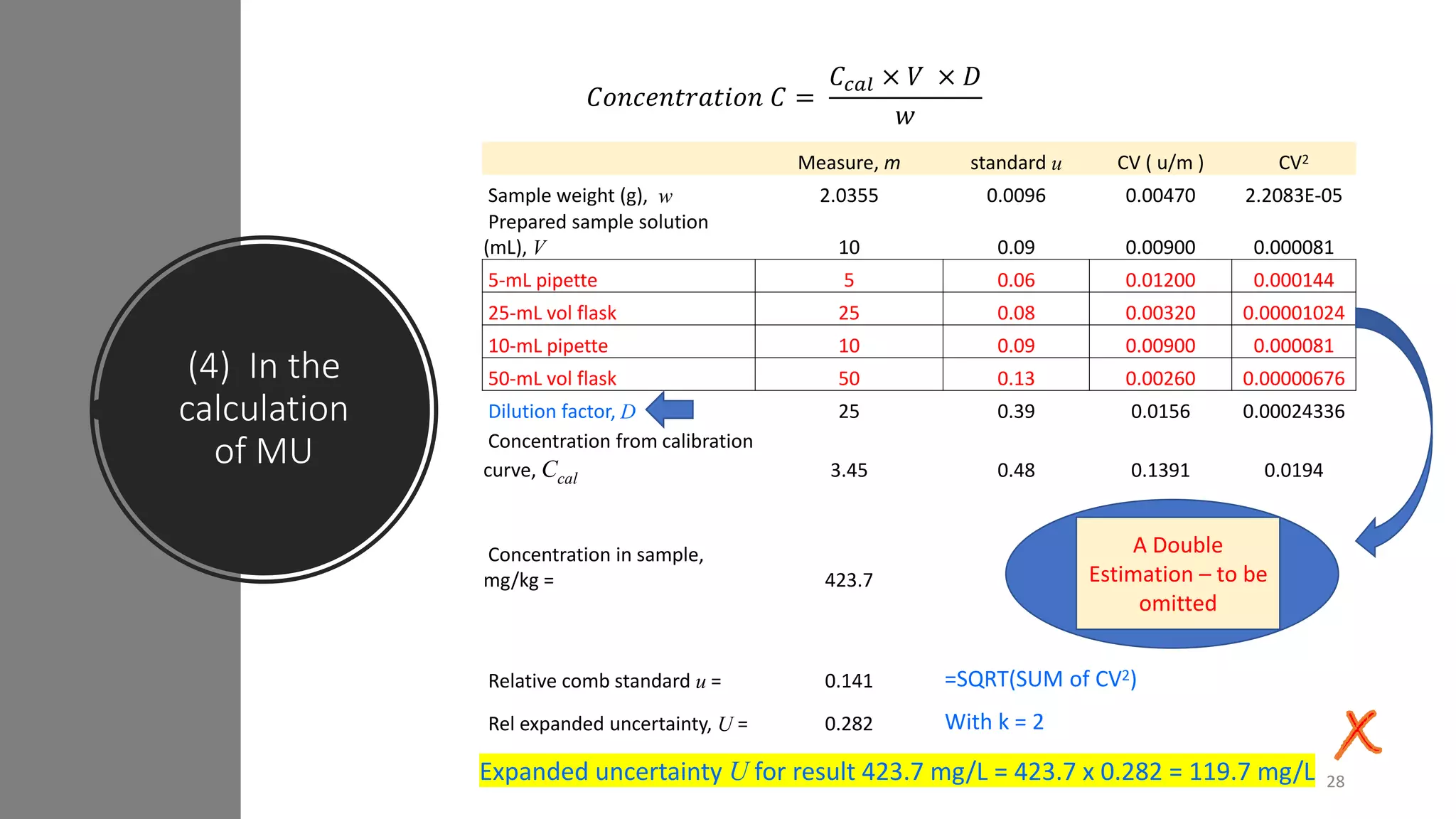
The document presents a webinar discussing common mistakes in evaluating measurement uncertainty (mu) in laboratory settings. It emphasizes the importance of understanding mu for accuracy, compliance with ISO standards, and confidence in test results, while also highlighting issues such as outdated reports and improper calculation methods. Key concepts include the propagation of uncertainty, the difference between bottom-up and top-down approaches, and the significance of consistent units in mu calculations.

1. Common mistakes in the
calculations of
measurement uncertainty
evaluation
via Zoom on Tuesday 15 June 2021 at
8:00 - 9:00pm Singapore (GMT +08)
by
Yeoh Guan Huah
https://consultglp.com
Welcome to the Free Webinar Series No. 9
1

2. Introduction
• In my years of experience as an External Lead Assessor and Technical
Assessor, I have noted the following situations in the subject of
measurement uncertainty (MU), namely:
• 1) All accredited laboratories have one way or another prepared MU evaluation
reports for their scope of testing for ISO compliance
• 2) Many do not seem to take the MU evaluation seriously as they don’t appreciate
the intention of this subject
• 3) Majority of the laboratories have adopted the tedious ISO GUM (bottom-up)
approach in the MU estimation; any top-down approach based on the overall
method performance in terms of repeatability, bias and reproducibility is preferred.
• 4) Many MU reports are outdated without regular review
• 5) Often, there are mistakes found in the process of MU evaluation, partly due to a
lack of full understanding of the MU concept.
2

3. Why must we treat
measurement
uncertainty evaluation
more seriously?
• To give a degree of confidence or
credibility on test results reported
• To interpret the test results against
specification or regulatory limits with
more confidence
• To compare two sets of laboratory for
technical competence
• To critically review a test method for
improvement
3

4. Back to basic: Why do we
carry out laboratory analysis?
• (A) An attempt to determine the “true value”
of the targeted analyte (measurand) in a
given sample
➢No measurement is exact
➢There is always an element of error in all
measurements due to uncontrollable
experimental factors
➢Error = | measured value – true value |
➢How are we to know if our measured value is
close to the true value of analyte
concentration in our sample? i.e., accuracy?
4

5. True value of
analyte in
sample
• In fact, we never know the analyte’s true
value in a given sample!
• However, we can analyse one or more of the
following similar samples containing known
values of analyte concurrently to provide a
test comparison:
• Assigned, known or given value
• Certified reference value by a third party (e.g.
CRM)
• Spiked value by adding known amount of
analyte to a matrix
• Consensus value by participating laboratories
from proficiency testing
• Note: these ‘true values’ also have their
associated uncertainties.
5

6. Go back to basic: Why do we
carry out laboratory analysis?
• (B) An attempt to infer what the analyte’s true value of the lot
(population) is where representative samples are supposed to
have been drawn from.
• The client is generally interested in knowing the analyte value
of his bulk materials (e.g. shipment), instead of the samples
sent for analysis
• What is your degrees of confidence when reporting test results
which are to be close to the true value in the population?
• In here, some probability distribution functions are applied.
• In other words, our measurement is to be accompanied with
some acceptable uncertainty, generally with 95% (0.95)
confidence or 5% (0.05) error or risk.
6

7. The definition of Measurement Uncertainty
• Definition (Source: International
Vocabulary of Basic and General Terms
in Metrology, VIM).
• Parameter, associated with the
result of a measurement, that
characterizes the dispersion of the
values that could reasonably be
attributed to measurand (analyte).
http://consultglp.com
True Value
The True Value is somewhere inside the range of X + U

8. Expression of measurement uncertainty (MU)
• Measurement uncertainty U is expressed as:
• Test result : X + U
• where, U = k x u
• where k is a coverage factor (usually k = 2 for 95% confidence under
normal probability distribution), and
• u, the combined standard uncertainty expressed as standard deviation.
• U is also called expanded uncertainty, assumed rightfully a normal
probability distribution of data
8

9. Important points to be noted in MU calculations
• All MU calculations are based on standard uncertainties, u,
expressed as standard deviations
• For a given uncertainty (expanded), U, we have first to convert
it to its standard uncertainty, u prior to MU calculation,
through:
• U  2 (assuming normal distribution), or
• U  3 (assuming rectangular distribution), or
• U  6 (assuming triangular distribution)
• The Law of Propagation of Standard Uncertainty is applied in
MU calculation.
9

10. Propagation Law of Standard Uncertainty (expressed
as standard deviation)
• A test method’s outcome, y involves many steps, and each step,
say xi can have a standard uncertainty, expressed as standard
deviation, u(xi), then y is a function of all the xi :
• y = f [x1, x2, x3, …, xn]
• The combined or total uncertainty variance of independent
components is:
• u(y)2 ={[f/x1]2u(x1)2 + [f/x2]2u(x2)2 + [f/x3]2u(x3)2 + .…}
𝑢(𝑦)2 = ෍
𝑖=1
𝑛
𝜕𝑓
𝜕𝑥𝑖
2
𝑢(𝑥𝑖)2
10
Sensitivity coefficient, ci
Total variance = sum of
contributing variances
In statistics,
Variance =
square of standard
deviation, s2 or u2

11. Propagation Law of Standard Uncertainty (expressed
as standard deviation)
• If the uncertainty or errors are NOT independent, there is an
extra covariance factor to be considered:
𝑢2
(𝑦) = ෍
𝜕𝑓
𝜕𝑥𝑖
2
𝑢(𝑥𝑖)2
+ ෍
𝜕𝑓
𝜕𝑥𝑖
𝜕𝑓
𝜕𝑥𝑗
𝐶𝑜𝑣 𝑥𝑖, 𝑥𝑗
Without consideration of covariance, the overall calculations are very much simplified.
11
Steps in analytical
methods are
independent to
each other. The
covariance effect
can be ignored.

12. ISO GUM approach in MU evaluation
• Most laboratories adopt this ISO GUM approach
• GUM stands for “Guide to the Expression of Uncertainty of
Measurement” - ISO/IEC Guide 98 / JCGM 100
• This approach takes all uncertainty contributors in each of the
testing steps into consideration
• The method’s mathematical model is the starting point for sourcing
uncertainty components
• Each of the test parameters in the mathematical equation is
quantifiable and hence its associated standard uncertainty
• For example:
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝐶 =
𝐶𝑐𝑎𝑙 × 𝑉 × 𝐷
𝑤
12

13. Propagation Law of Standard Deviations simplified
• Linear Combination of standard deviations
• y = K(a + b – c) with std deviations ua, ub, uc and K is a
constant factor (or a fixed value such as 100),
• then, the total variance of y is:
• sy
2= K x ( ua
2 + ub
2 + uc
2 )
• therefore, the combined standard deviation sy is
• sy = K x √( ua
2 + ub
2 + uc
2 )
• Note : components a, b and c must be of same unit and involve
in addition / subtraction
13
Note:
Variance =
square of standard
deviation, s2 or u2

14. Example 1 on linear combination of uncertainties
• Combined standard uncertainty 𝑢 = 0.232 + 0.232 = 0.325mL
Burette
volume, mL
Burette Std
u , mL
Volume after titration (mL) 18.80 0.23
Volume before titration (mL) 10.00 0.23
Volume of titrant (mL) 8.80 ?
14

15. A quick revision of differentiation function in Calculus
• Before studying the multiplication and division calculations for MU,
let’s revise our knowledge of differentiation in Calculus:
• Given y = x
Then,
𝛿𝑦
𝛿𝑥
= 1𝑥(1−1)
= 1
Given y = x2
Then,
𝛿𝑦
𝛿𝑥
= 2𝑥(2−1)
= 2𝑥
Given 𝑦 =
1
𝑥
= 𝑥−1
Then,
𝛿𝑦
𝛿𝑥
= −𝑥 −1−1
= −𝑥−2
= −
1
𝑥2
15

16. Propagation Law of Standard Uncertainty
• Multiplicative Combination
• 𝑦 = 𝐾
𝑃×𝑉
𝑇
with std deviations
uP , uV , uT and K is a constant
factor, then,
• 𝑐𝑃 =
𝜕𝑦
𝜕𝑃
= 𝐾
𝑉
𝑇
• 𝑐𝑉 =
𝜕𝑦
𝜕𝑉
= 𝐾
𝑃
𝑇
• 𝑐𝑇 =
𝜕𝑦
𝜕𝑇
= −𝐾
𝑃×𝑉
𝑇2
16
𝑢2 𝑦 = 𝑐𝑃
2
𝑢2 𝑃 + 𝑐𝑉
2
𝑢2 𝑉 + 𝑐𝑇
2
𝑢2 𝑇
= (𝐾
𝑉
𝑇
)2
𝑢2
𝑃 + (𝐾
𝑃
𝑇
)2
𝑢2
𝑉 + (−𝐾
𝑃𝑉
𝑇2)2
𝑢2
(𝑇)
Dividing both sides by 𝑦2 = (𝐾
𝑃×𝑉
𝑇
)2 gives:
(
𝑢(𝑦)
𝑦
)2 = (
𝑢(𝑃)
𝑃
)2+ (
𝑢(𝑉)
𝑉
)2 + (
𝑢(𝑇)
𝑇
)2, or
𝑢(𝑦)
𝑦
= (
𝑢(𝑃)
𝑃
)2+ (
𝑢(𝑉)
𝑉
)2 + (
𝑢(𝑇)
𝑇
)2
𝐶𝑉
𝑦 = 𝐶𝑉
𝑝
2
+ 𝐶𝑉𝑉
2
+ 𝐶𝑉𝑇
2
𝐶𝑉 =
𝑠 (𝑜𝑟 𝑢)
ҧ
𝑥

17. Propagation Law of Standard Uncertainty
• Multiplicative Combination
• y = K(a x b) / c with std deviations ua, ub, uc and K is a
constant factor,
• Then, the combined standard deviation uy is
• or,
• Where is the constant factor K in the above equation?
17
𝑢𝑦
𝑦
= (
𝑢𝑎
𝑎
)2+ (
𝑢𝑏
𝑏
)2 + (
𝑢𝑐
𝑐
)2
𝑢𝑦 = 𝑦 (
𝑢𝑎
𝑎
)2+ (
𝑢𝑏
𝑏
)2 + (
𝑢𝑐
𝑐
)2

18. Example 2 on multiplicative combination of uncertainties
Value, V Std u
a 22.5 mg/L 0.2 mg/L
b 250 mL 1.2 mL
w 100 gm 0.8 gm
Y 56.25 mg/kg ?
• Y = (a x b) / w
• uy / Y = √ (ua / a)2 + (ub / b)2 + (uw / w)2
• Answer : uy = 0.725 mg/kg
18
𝑢𝑦 = 𝑌 (
𝑢𝑎
𝑎
)2+ (
𝑢𝑏
𝑏
)2 + (
𝑢𝑤
𝑤
)2

19. Common mistakes in MU calculations – can you spot them?
(1)
Weight, w
in g
Std uncertainty, u
in mg
Wt of crucible + sample 53.3345 6.55
Wt of crucible 33.3243 6.55
Wt of sample 20.0102 9.26
Relative combined
standard uncertainty as
coefficient of variation, CV
as a weighing uncertainty
component = 9.26 / 20.0102 = 0.463
= 6.552 + 6.552
19

20. Answer to Mistake (1)
Weight, w
in g
Std uncertainty, u in
g
Wt of crucible + sample 53.3345 0.00655
Wt of crucible 33.3243 0.00655
Wt of sample 20.0102 0.00926
Relative combined
standard uncertainty as
coefficient of variation, CV
as a weighing uncertainty
component = 0.00926 / 20.0102 = 0.000463
Difference
in units (g
and mg)
20

21. Common mistakes in MU calculations – can you spot them?
(2)
Uncertainty component Measure, m standard u
Sample weight (g), w 10.0455 0.0096
Prepared solution (mL), V 25.03 0.18
Dilution factor, D 20 0.26
Concentration from calibration curve (mg/L),
Ccal 4.55 0.39
Concentration in sample, mg/kg = 226.7 =(4.55x25.03x20)/10.0455
Combined std uncertainty, u = 0.502
=SQRT(0.00962+0.182+0.262+
0.392)
Expanded uncertainty, U = 1.004 With k = 2
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝐶 =
𝐶𝑐𝑎𝑙 × 𝑉 × 𝐷
𝑤
21

22. Answer to Mistake (2)
Uncertainty component Measure, m standard u CV ( u/m ) CV2
Sample weight (g), w 10.0455 0.0096 0.00095 9.0668E-07
Prepared solution (mL), V 25.03 0.18 0.00719 5.1716E-05
Dilution factor, D 20 0.26 0.013 0.000169
Concentration from calibration
curve (mg/L), Ccal 4.55 0.39 0.0857 0.0073
Concentration in sample, mg/kg = 226.7 =(4.55x25.03x20)/10.0455
Relative comb standard u/Conc = 0.087 =SQRT(SUM of CV2)
Rel expanded uncertainty = 0.174 With k = 2
Expanded uncertainty U for result 226.7 mg/L = 226.7 x 0.174 = 39.5 mg/L
𝑢𝑐 = 𝐶 (
𝑢𝑤
𝑤
)2+ (
𝑢𝑉
𝑉
)2 + (
𝑢𝐷
𝐷
)2 + (
𝑢𝑐𝑎𝑙
𝐶𝑐𝑎𝑙
)2
22

23. Common mistakes in MU calculations – can you spot them?
(3)
Uncertainty component Measure, m standard u CV ( u/m ) CV^2
Intermediate repeatability std deviation 225.4 31.2 0.1384 0.0192
Sample weight (g), w 10.0455 0.0096 0.00095 9.0668E-07
Prepared solution (mL), V 25.03 0.18 0.00719 5.1716E-05
Dilution factor, D 20 0.26 0.013 0.000169
Concentration from calibration curve
(mg/L), Ccal 4.55 0.39 0.0857 0.0073
Concentration in sample = 226.7
Relative comb standard u = 0.163
Expanded uncertainty, U = 0.327
Expanded uncertainty U for result 226.7 mg/L = 226.7 x 0.327 =
74.1 mg/L
23

24. Answer to Mistake (3)
• Intermediate repeatability standard deviation is a measure of
total method performance in terms of precision, which is a top-
down approach
• The others were calculated from the estimates of standard
uncertainty of each step of the test method, which is referred to
as the GUM or a bottom-up approach.
• These two approaches should not be used at the same time.
• If not, we would have doubly estimated the measurement
uncertainty.
24

25. Answer to Mistake (3)
Uncertainty component Measure, m standard u CV ( u/m ) CV^2
Intermediate repeatability std deviation 225.4 31.2 0.1384 0.0192
Sample weight (g), w 10.0455 0.0096 0.00095 9.0668E-07
Prepared solution (mL), V 25.03 0.18 0.00719 5.1716E-05
Dilution factor, D 20 0.26 0.013 0.000169
Concentration from calibration curve
(mg/L), Ccal 4.55 0.39 0.0857 0.0073
Concentration in sample = 226.7
Relative comb standard u = 0.087
Expanded uncertainty, U = 0.174
Expanded uncertainty U for result 226.7 mg/L = 226.7 x 0.174 = 39.5 mg/L
25

26. Another common mistake in MU calculations (4)
• In a trace metal analysis, a 2 g sample was taken to be acid digested,
filtered and made up to 10 ml in a volumetric flask with distilled
water. Further 25x dilution was required for the instrumental
analysis to fit into the plotted linear calibration curve.
• Dilution steps:
• Pipette 5-mL of the digested sample solution into 25-mL volumetric
flask and make up to the mark (intermediate solution, 5x dilution)
• Pipette 10-mL intermediate solution into 50-mL volumetric flask and
make up to the mark (test solution, 5x dilution)
• Dilution factor: 5 x 5 = 25
26

27. (4) Estimating combined standard u of the dilution factor
Value, V Uncertainty, U
Coverage
factor, k
Standard
uncertainty, u u/V (u/V)2
5-mL pipette 5 0.12 2 0.06 0.012 0.000144
25-mL vol flask 25 0.16 2 0.08 0.0032 1.02E-05
10-mL pipette 10 0.18 2 0.09 0.009 0.000081
50-mL vol flask 50 0.26 2 0.13 0.0026 6.76E-06
Sum SQs = 0.000242
SQRT = 0.0156
Dilution factor = 25
Combined std u = 0.39 =25 x 0.0156 𝑢𝐷 = 𝐶 (
𝑢5
5
)2+ (
𝑢25
25
)2 + (
𝑢10
10
)2 + (
𝑢50
50
)2
27

28. (4) In the
calculation
of MU
Measure, m standard u CV ( u/m ) CV2
Sample weight (g), w 2.0355 0.0096 0.00470 2.2083E-05
Prepared sample solution
(mL), V 10 0.09 0.00900 0.000081
5-mL pipette 5 0.06 0.01200 0.000144
25-mL vol flask 25 0.08 0.00320 0.00001024
10-mL pipette 10 0.09 0.00900 0.000081
50-mL vol flask 50 0.13 0.00260 0.00000676
Dilution factor, D 25 0.39 0.0156 0.00024336
Concentration from calibration
curve, Ccal 3.45 0.48 0.1391 0.0194
Concentration in sample,
mg/kg = 423.7
Relative comb standard u = 0.141 =SQRT(SUM of CV2)
Rel expanded uncertainty, U = 0.282 With k = 2
Expanded uncertainty U for result 423.7 mg/L = 423.7 x 0.282 = 119.7 mg/L
A Double
Estimation – to be
omitted
𝐶𝑜𝑛𝑐𝑒𝑛𝑡𝑟𝑎𝑡𝑖𝑜𝑛 𝐶 =
𝐶𝑐𝑎𝑙 × 𝑉 × 𝐷
𝑤
28

29. (5) Common mistakes in estimating MU for
microbiological counts
• Quantitative discrete data (e.g. bacterial colony counts and
MPNs) do not conform to a normal distribution
• They need a transformation to “normalize” the data before
analysis
• Transformation: converting each raw cfu/g data value (xi) into
the log10 value (yi) where
yi= log10(xi)
• Actually, it is more correct to use the natural logarithmic
transformation (i.e. yi = ln xi) with a natural number e = 2.718
29

30. Common mistakes in estimating MU for
microbiological counts
• Calculation examples of counts, xi in cfu/g:
xi y = log10(xi)
10 1.000
100 2.000
250 2.398
1000 3.000
5000 3.699
Note: To anti-log10(y), use 10y
30

31. MU Estimation method for microbiological colony counts
𝑢𝑟𝑒𝑙
2
=
σ 𝐿𝑜𝑔𝑎 − 𝐿𝑜𝑔𝑏
2
/𝐿𝑜𝑔( ҧ
𝑥)
2 × 𝑛
𝑢𝑟𝑒𝑙 =
σ 𝐿𝑜𝑔𝑎 − 𝐿𝑜𝑔𝑏
2/𝐿𝑜𝑔( ҧ
𝑥)
2 × 𝑛
31

32. Other common issues in MU calculations
• (1) No consideration for other uncertainty contributors, which are
significant in affecting the output (test result), apart from the
parameters in the mathematical equation of the test method.
• Example:
• Kinematic viscosity (KV) of fuel oil (cst) = c x t , where c = certified
constant value for viscometer, with standard uncertainty uc, and t, time in
seconds with standard uncertainty ut, at a fixed temperature (ASTM
D445)
• Therefore,
𝑢𝑉
𝑉
=
𝑢𝑐
𝑐
2
+
𝑢𝑡
𝑡
2
• By this calculation, the combined standard uncertainty, uKV is found to be
very small, about 0.2 cst for an average viscosity value of 180 cst.
32

33. Other common issues in MU calculations
• However, temperature variation is known to affect the flow of liquid, i.e. its
viscosity
• So, two other uncertainty factors, though not in the original equation for
calculations, are to be considered:
• (1) the std uncertainty of the observed temperature T as shown by the
calibrated thermometer held in the oil bath, uT
• (2) the temperature variation in the oil bath with mechanical stirring, uTVar
• Hence, the proper MU evaluation is to be:
•
𝑢𝑉
𝑉
=
𝑢𝑐
𝑐
2
+
𝑢𝑡
𝑡
2
+
𝑢𝑇
𝑇
2
+
𝑢𝑇𝑉𝑎𝑟
𝑇𝑉𝑎𝑟
2
• By doing so, the combined standard uncertainty uKV is about 0.6 cst for an
average value of 180 cst.
33

34. Other common issues in MU calculations
• (2) The MU reports have not been reviewed at regular intervals.
• During assessment, some lab MU reports using the GUM bottom-up
method were found to be dated some 5 – 10 years ago without any
intermediate review.
• During this long period,
• the lab instrument might have been upgraded,
• the calibration standards might have been obtained from different suppliers,
• the technicians might have been changed, and
• the lab environment might be very different, due to relocation.
• Solution: To review MU as and when there is a major change in
operating the test method.
34

35. Parting words in conclusion
….
one must take MU evaluation
even more seriously.
• We must aim to make not more than 5% risk or error to
declare a test result to be off-specification in order to be
95% confidence in making the statement.
35
A more realistic uncertainty value of a measurement can surely affect your decision to state
a Pass or Fail against the given specification limit.