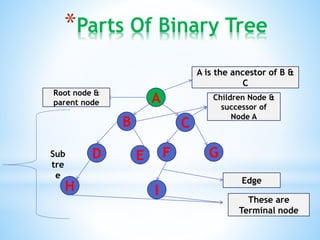
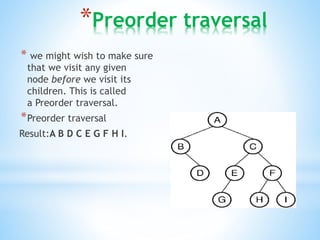
A binary tree is a data structure made up of nodes where each node contains data and pointers to left and right child nodes. It can be empty or consist of a single root node with binary trees as subtrees. Binary trees can be traversed in preorder, inorder, or postorder to process nodes. Properties include the height, depth, degree of nodes, and whether the tree is complete, extended, or a binary search tree. Heaps are binary trees that satisfy the heap property of being either min or max heaps.

1. *

2. What Is Binary Tree?
*A binary tree is made of nodes, where each node
contains a "left" pointer, a "right" pointer, and a
data element. The "root" pointer points to the
topmost node in the tree. The left and right
pointers recursively point to smaller "sub-trees" on
either side. A null pointer represents a binary tree
with no elements -- the empty tree. The formal
recursive definition is: a binary tree is either empty
(represented by a null pointer), or is made of a
single node, where the left and right pointers
(recursive definition ahead) each point to a binary
tree.

3. *Parts Of Binary Tree
A
B C
FD GE
H I
Root node &
parent node
Children Node &
successor of
Node A
Sub
tre
e
A is the ancestor of B &
C
Edge
These are
Terminal node

4. *Complete Binary Tree
*A complete binary tree is a binary tree in which every
level, except possibly the last, is completely filled, and
all nodes are as far left as possible

5. *Extended Binary Tree
*A binary tree in which special nodes are added
wherever a null subtree was present in the
original tree so that each node in the original
tree (except the root node)

6. *Traversing Binary Tree
*Often we wish to process a binary tree by "visiting"
each of its nodes, each time performing a specific
action such as printing the contents of the node.
Any process for visiting all of the nodes in some
order is called a Traversal.

7. *Preorder traversal
* we might wish to make sure
that we visit any given
node before we visit its
children. This is called
a Preorder traversal.
*Preorder traversal
Result:A B D C E G F H I.

8. *In order Traversal
*An In order Traversal first visits the left
child (including its entire subtree), then
visits the node, and finally visits the right
child (including its entire subtree).
The binary search trees makes use of this
traversal to print all nodes in ascending
order of value.
Inorder result:
B D A G E C H F I.

9. *Post-Order Traversal
*we might wish to visit each node only after we visit its
children (and their subtrees). For example, this would
be necessary if we wish to return all nodes in the tree
to free store. We would like to delete the children of a
node before deleting the node itself. But to do that
requires that the children's children be deleted first,
and so on. This is called a postorder Traversal.
*Post order resullt:D B G E H I F C A.

10. *Depth Of Node
*The depth of a node is the number of edges from the
root to the node. The height of a node is the number of
edges from the node to the deepest leaf. The height of
a tree is a height of the root. A full binary tree.is a
binary tree in which each node has exactly zero or two
children.

11. *Degree Of Tree
*The number of subtrees of a node is called
the degree of the node. In a binary tree,
all nodes have degree 0, 1, or 2.
A node of degree zero is called a terminal node or
leaf node. A non-leaf node is often called a
branch node.
*For this tree the degree of “A” is 2.

12. *Height Of Tree
*The height of a node is the number of edges on
the longest path from the node to a leaf.
*Here the Height of the tree is
3(H).
A
CB
GD E F
H

13. *Binary Search Tree
*A binary search tree (BST) is a binary
tree where each node has a Comparable
key (and an associated value) and satisfies
the restriction that the key in any node is
larger than the keys in all nodes in that
node's left subtree and smaller than the
keys in all nodes in that node's right
subtree.

14. *Heap
*A binary heap is a complete binary tree
which satisfies the heap ordering property.
The ordering can be one of two.
1.Max heap
2.Min heap

15. *Max Heap
*A max-heap is a complete binary tree in which the value in each
internal node is greater than or equal to the values in the
children of that node.

16. *Min Heap
*the value of each node is greater than or equal
to the value of its parent, with the minimum-
value element at the root.