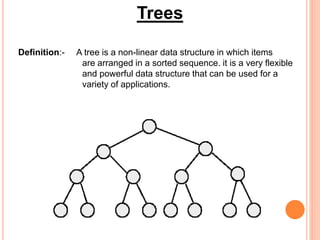
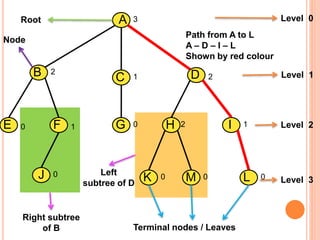
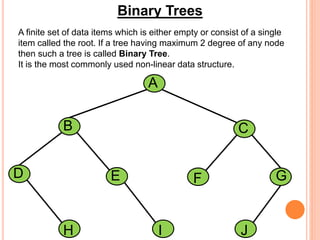
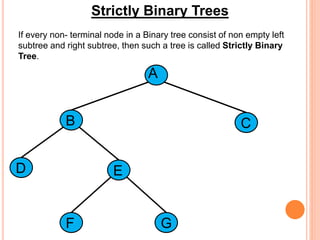
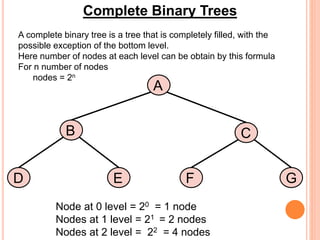
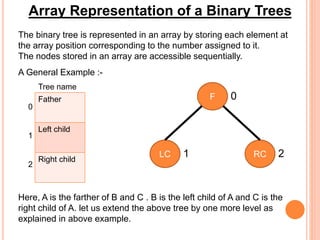
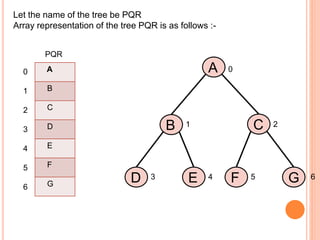
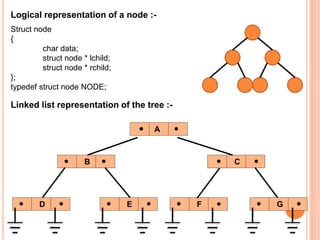
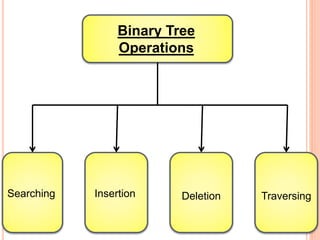
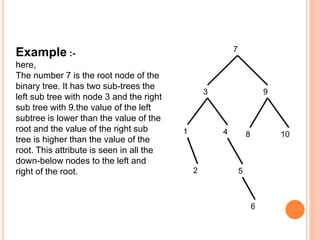
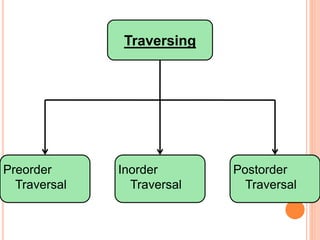
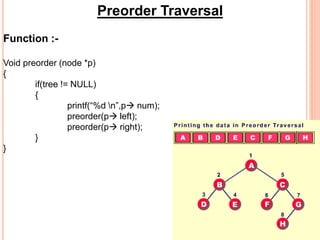
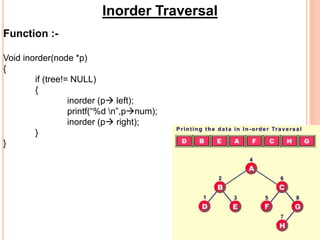
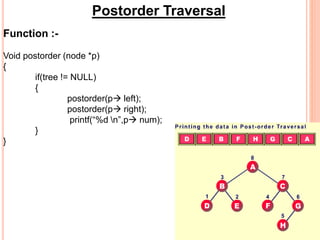
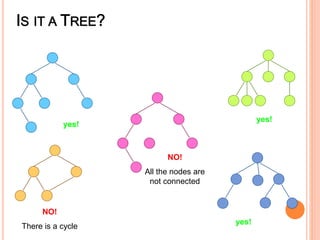
This document discusses data structures and binary trees. It begins with basic terminology used in trees such as root, node, degree, levels, and traversal methods. It then explains different types of binary trees including strictly binary trees and complete binary trees. Next, it covers binary tree representations using arrays and linked lists. Finally, it discusses operations that can be performed on binary search trees including insertion, searching, deletion, and traversing nodes using preorder, inorder and postorder traversal methods.

1. Data
Structures

2. CONTENTS
1) Introduction to Trees.
2) Basic terminologies
3) Binary tree
4) Binary tree types
5) Expressions in binary tree
6) Binary tree representation
7) Binary search tree
8) Creation of a binary tree
9) Operations on binary search tree
Trees

3. Trees
Definition:- A tree is a non-linear data structure in which items
are arranged in a sorted sequence. it is a very flexible
and powerful data structure that can be used for a
variety of applications.

4. 1. Root:- The node at the top It is the main.
2. Node :-An element in the tree references data and other nodes.
3. Degree of a node :-The number of sub trees of a node.
4. Degree of tree:- The maximum degree of nodes.
5. Terminal nodes /Leaves:- Nodes with no children.
6. Non-terminal nodes:- Any node whose degree is not zero.
7. Levels:- The root is at level 0, and its child are at level 1.
8. Child:- The node(s) below a given node.
9. Parent :-The node directly above another node (except root).
10. Edge:- A connecting line of two nodes.
11. Path:- A sequence of consecutive edges.
12. Depth/Height:- It is the maximum level of any node.
13. Forest:- It is a set of disjoint trees.
Some Basic Terminologies

5. A
B C D
GE
L
I
Root Level 0
Level 1
Level 2
Level 3
Node
Terminal nodes / Leaves
F
J
H
K M
Right subtree
of B
Left
subtree of D
Path from A to L
A – D – I – L
Shown by red colour
3
1
2
2
1
00 0
0
1
0
0 2

6. Binary Trees
A finite set of data items which is either empty or consist of a single
item called the root. If a tree having maximum 2 degree of any node
then such a tree is called Binary Tree.
It is the most commonly used non-linear data structure.
D
A
B
E
H I
C
J
GF

7. Strictly Binary Trees
If every non- terminal node in a Binary tree consist of non empty left
subtree and right subtree, then such a tree is called Strictly Binary
Tree.
D
A
B
E
F G
C

8. Complete Binary Trees
A complete binary tree is a tree that is completely filled, with the
possible exception of the bottom level.
Here number of nodes at each level can be obtain by this formula
For n number of nodes
nodes = 2n
D
A
B
E F G
C
Node at 0 level = 20 = 1 node
Nodes at 1 level = 21 = 2 nodes
Nodes at 2 level = 22 = 4 nodes

9. Expressions in Binary Trees
It consists of operands and binary operators. In a tree we go from left
to right as explained further through an example.
*
C
Example:-
As above said the tree
representation is read from left to
right so if we consider the fig.Q.1
then the left sub tree shows that
(A+B) then the resultant figure is
fig. Q.2
Now if we again solve it then it will
finally become. (A+B)*C.
Finally expression of this binary
tree is (A+B)*C
Fig.Q.1
*
(A+B) C
Fig.Q.2
+
A B
Left Sub-tree

10. Array
Representation
Linked List
Representation
Binary Tree
Representation

11. Array Representation of a Binary Trees
The binary tree is represented in an array by storing each element at
the array position corresponding to the number assigned to it.
The nodes stored in an array are accessible sequentially.
Father
Left child
Right child
0
1
2
Tree name
F
RCLC
0
1 2
A General Example :-
Here, A is the farther of B and C . B is the left child of A and C is the
right child of A. let us extend the above tree by one more level as
explained in above example.

12. D
A
B
E F G
C
A
B
C
D
E
F
G
Let the name of the tree be PQR
Array representation of the tree PQR is as follows :-
0
6543
1 2
0
1
2
3
4
5
6
PQR

13. Linked List Representation of a Binary Trees
Binary trees can be represented by Linked list also. The basic
component to be represented in a binary tree is a node.
Node is consist of three parts:-
 Data
 Left child
 Right child
Lchild Data Rchild

14. Linked list representation of the tree :-
A
FE GD
CB
Struct node
{
char data;
struct node * lchild;
struct node * rchild;
};
typedef struct node NODE;
Logical representation of a node :-

15. Binary Tree
Operations
InsertionSearching Deletion Traversing

16. Binary Search Trees
A Binary search tree is a binary tree which is either empty or satisfies the
following rules :-
1. The value of the key in the Lchild or Left subtree is less than the value
of the root.
2. The value of the root key in the Rchild or Right subtree is more than
or equal to the value of the root.
3. All the sub-trees of the Left and Right children observe the two rules.
9
125
10208

17. 7
93
108
6
5
4
2
1
Example :-
here,
The number 7 is the root node of the
binary tree. It has two sub-trees the
left sub tree with node 3 and the right
sub tree with 9.the value of the left
subtree is lower than the value of the
root and the value of the right sub
tree is higher than the value of the
root. This attribute is seen in all the
down-below nodes to the left and
right of the root.

18. Binary Search Of A Node
Function for binary search of a node
Void search(node * p, long digit)
{
if(p==NULL)
printf(“The number does not exist n”);
elseif(digit==p num)
printf(“number =%d n”,digit);
elseif(digit<p num)
search (p left, digit);
else
search (p right, digit);
}

19. Example Of Insertion
Draw a binary search tree by inserting the above numbers from left to right.
11, 6, 8, 19, 4, 10, 5, 17, 43, 49, 31
6
11
5
4 8
10
19
17 43
4931

20. Insertion of nodes in a binary search tree
Function :-
Void insertion(node * p, int digit)
{
if(p==NULL)
{
p=(node*) malloc (sixe of(node));
p left = p right = NULL;
p num = digit;
}
elseif (digit < p num)
p left = insert(p left, digit);
elseif (digit > p num)
p right = insert(p right, digit);
elseif (digit == p num)
printf(“Duplicate node : program exited”); exit(0);
return (p);
}

21. Example Of Deletion:-
case 1: Node with no children (or) leaf node
case 2: Node with one child
case 3: Node with two children.
20
/
13 23
/ /
9 14 21 27
/
19 24

22. Case 1: Delete a leaf node/ node with no children.
20
/
13 23
/ /
9 14 21 27
/
19 24
Delete 24 from the above binary search tree.
20
/
13 23
/ /
9 14 21 27
19

23. Case 2: Delete a node with one child.
20
/
13 23
/ /
9 14 21 27
/
19 24
Delete 14 from above binary search tree.
20
/
13 23
/ /
9 19 21 27
/
24

24. Case 3: Delete a node with two children.
Delete a node whose right child is the smallest node in the right sub-tree. (14 is
the smallest node present in the right sub-tree of 13).
20
/
13 23
/ /
9 14 21 27
/
19 24
Delete 13 from the above binary tree. Find the smallest in the left subtree of
13. So, replace 13 with 14.
20
/
14 23
/ /
9 19 21 27
/
24

25. Deletion of nodes in a binary search tree
Function:-
Node *delnum (int digit, node *r)
{
node *q;
If(r right !=NULL)
delnum(digit, rright);
else
qnum = r num;
q = r;
q = r left;
}
Node *deletenode(int digit, node *p)
{
node *r, *q;
if(p == NULL)

26. {
printf(“p is empty n”);
exit(0);
}
if(digit < p  num)
deletenode(digit, p  left);
elseif(digit> p  num)
deletenode (digit, p  right);
q = p;
if((q  right == NULL) && (q  left == NULL))
q = NULL;
elseif(q  right == NULL)
p = q  left;
elseif(q  left == NULL)
p = q  right;
else
deletenum(digit, q  left);
free(q);
}

27. Traversing
Traversing may be defined as the rules of finding the node
combination in a given binary tree. The rules will be such as to
define the nodes and its children.

28. Traversing
Preorder
Traversal
Postorder
Traversal
Inorder
Traversal

29. Preorder Traversal
Function :-
Void preorder (node *p)
{
if(tree != NULL)
{
printf(“%d n”,p num);
preorder(p left);
preorder(p right);
}
}

30. Inorder Traversal
Function :-
Void inorder(node *p)
{
if (tree!= NULL)
{
inorder (p left);
printf(“%d n”,pnum);
inorder (p right);
}
}

31. Postorder Traversal
Function :-
Void postorder (node *p)
{
if(tree != NULL)
{
postorder(p left);
postorder(p right);
printf(“%d n”,p num);
}
}

32. yes!
NO!
All the nodes are
not connected
NO!
There is a cycle
yes!
yes!

33. Thank You