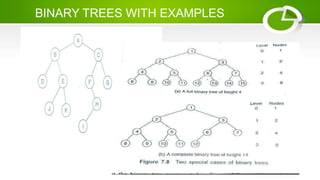
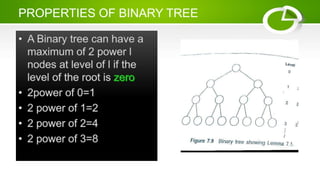
The document discusses binary trees, including their basic terminology, properties, representations, traversal methods, and common operations. It provides algorithms for inserting nodes, deleting nodes, and merging two binary trees. The key points covered are: - Binary trees have a root node, child nodes, and properties like maximum/minimum number of nodes based on height. - They can be represented sequentially using arrays or non-sequentially using linked lists. 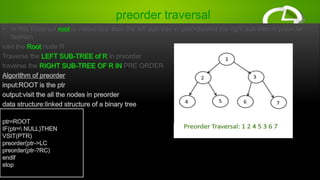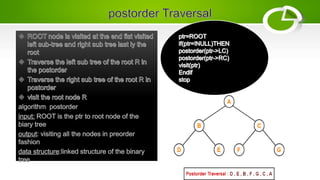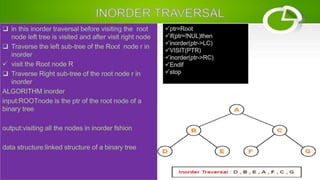- Common traversal orders are preorder, inorder, and postorder. 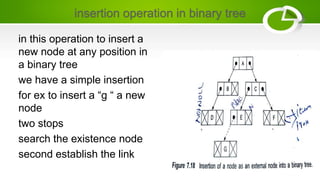- Operations include insertion, deletion, traversal, and merging two trees into one larger tree. - Algorithms are presented for inserting nodes using linked lists and merging two trees by combining their nodes.

1. v.lavanya
MSC I T

2. OBJECTIVES

3. root node is desigated wich has no parent
if the imediate predecessor of the node is parent of the node then all imediate sucessor of a node
are known as child
child which is on left side is called left child and hat on right side is called
right child
Basic terminolgies

5. BINARY TREES WITH EXAMPLES

6. PROPERTIES OF BINARY TREE

7.  the maximum no of nodes
possible in a binary tree of
height h is 2power of h-1
The minimum no of nodes
possible in a binary tree Height
h is h
a binary tree has the minimum
no of nodes one every parent
has one child such kind of
trees are called skew binary
trees

8. LINEAR ARRAY
NONLINEAR
LINKED LIST

9. • The root N of T is stored
in TREE [1]. If a node
occupies TREE [k] then its
is stored in TREE
and its is
stored into TREE

10. Advantage of sequential rpresentation
any node can acessed from any other node by calculating the
index value
data are stored without any pointers to their
which are mentioned implicity
programing lanuage where dynamic memmory allocation is not
possible such as(BASIC ,FORTRAIN)ARRAY
REPREPRESENTAION IS nly means to store a tree

11. Disadvantage of sequential reprentation
other then the full of binary trees the majority of the array entries
may be empty
it allows only static representation it is in no way possible to
enhance the tree structure if the array size will be limited
insering new node to the tree or deleting a node in a tree data
moved up and moved down in an array excessive amount of
processing time

12. linked list representation
of a binary tree they are two field s
to stor the address of left child
and right child of the node
data is the current
information of the node
if one knows the address of the root node
then form it other node can be acessed

13. physical implementation of a binary tree in memmory
Algorithm build a tree
input:ITEM is the data contet of the node i
output: a binary tree with two sub-trees of the node i
data structure: array representation of a binary tree

14. operations of binary trees
 insertion: TO include a node into an existing binary tree
deletion: TO delete a node from a non-empty binary tree
Traversal: TO visit all the nodes in abinary tree
in traversal they are three orders
inorder -> LEFT->ROOT->RIGHT
preorder -> ROOT->LEFT->RIGHT
postorder-> LEFT->RIGHT->ROOT
merge:TO merge two binary trees into a large one

15. in this operation to insert a
new node at any position in
a binary tree
we have a simple insertion
for ex to insert a “g “ a new
node
two stops
search the existence node
second establish the link

17. insert a binary tree using linked list
• insert:KEY is the data content of the key node after new node is
to be inserted an ITEM is the data content of the new node can
be inserted
• output: A node with data component ITEM inserted as an
extrernal node after the node having data KEY if such a node
does not exist with empty (s), that is, eiter child or both children
IS/ARE ABSENT.
• DATA STRUCTURE: linked structure of a binary tree. ROOT is
the pointer to the root node.

19. algorithm
• PRINT “ insertion is not possible as left child”
• EXIT
• EDIF
• ELSE
• IF(pf->RC =NULL)
• new=GETNODE
• new->DATA=ITEM
• new->LC=new->RC=NULL
• ptr->RC=new
• else
• print”insertion is not possibble as right child”
• exit
• end if
• else
• print”the key node is already has a child”
• stop

20. deletion
• in deletion operation can be carried out of two kinds of storage
representation of binary trees
• in ordernto delete a node in a binary tree it is required to reach at
the parent node to be deleted
• the link of the parent nodes whih stores the location of the node
to be deleted is then set buy a NULL entry
• input:given ITEM as data of the node with which the node can be
identified for deletion
• output:a binary tree without a node having a data ITEM
• data stucture: array a storing binary trees SIZE denotes the size
of a

22. WHAT IS A TRAVERSAL?
THE traversal operation is frequently used operation of a binary
this operation to visit each node in the tree exactly once
a full traversal of a binary tree gives a linear ordering of the data
in the tree
if a binary tree contains an arithmetic expression then it traverse
infix notations,posfix notations,prefix notations

23. preorder traversal

27. input:two pointers ROOT1 and
ROOT2 OF THE TWO BINARY
TREES t1,t2
output:a binary treee containing all
the node t1,t2 ptr to the root as
ROOT
data structure:linked the data
strucure
steps:
if(ROOT1=NULL)THEN
ROOT=ROOT2
EXIT