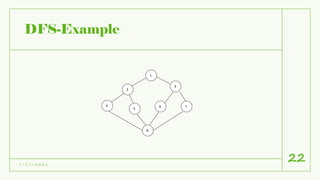
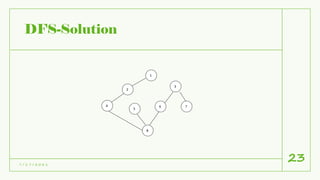
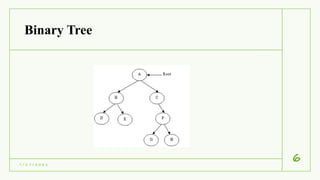
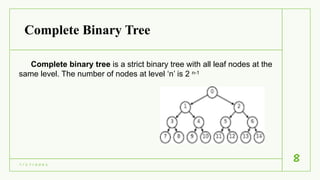
The document discusses graph and tree traversals. It defines trees and graphs, and describes common tree traversals like preorder, inorder and postorder. It also describes two graph traversal algorithms - breadth-first search (BFS) and depth-first search (DFS). BFS uses a queue to visit vertices level-wise, while DFS uses a stack to go deep down one path before backtracking. Examples of BFS and DFS on graphs are shown. Applications of the traversal algorithms include checking connectivity, cycles and finding reachable vertices in a graph.

1. Ms.Mary Jacob
Assistant Professor, Department of Computer Science
Kristu Jayanti College(Autonomous), Bangalore
Graph Traversals

2. Definitions
7 / 1 7 / 2 0 2 1
2
A Tree is a data structure that emulates a hierarchical tree structure with a set of
linked nodes.
It is a data structure accessed beginning at the root node. Each node is either a
leaf or an internal node. An internal node has one or more child nodes and is
called the parent of its child nodes. All children of the same node are siblings.

3. Formal Definitions
7 / 1 7 / 2 0 2 1
3
A tree is either empty (no nodes), or a root and zero or more sub trees.
Tree Terminologies
 Root: node without parent (A) , node at the top of the tree
 Internal node: node with at least one child (A, B, C, F)
 External node: a kind of leaf node without children (E, I, J, K, G, H, D)
 Ancestors of a node: parent, grandparent, grand-grandparent, etc
 Depth of a node: number of ancestors
 Height of a tree: maximum depth of any node (3)
 Descendant of a node: child, grandchild, grand-grandchild, etc
 Degree of an element: no. of children it has
 Sub tree: tree consisting of a node and its descendants
 Path: traversal from node to node along the edges that results in a sequence

4. Formal Definitions
7 / 1 7 / 2 0 2 1
4
 Parent: any node, except root has exactly one edge running upward to another node. The node
above it is called parent.
 Child: any node may have one or more lines running downward to other nodes. Nodes below
are children.
 Leaf: a node that has no children
 Sub tree: any node can be considered to be the root of a subtree, which consists of its children
and its children's children and so on.
 Visiting: a node is visited when program control arrives at the node, usually for processing.
 Traversing: to traverse a tree means to visit all the nodes in some specified order.
 Levels: the level of a particular node refers to how many generations the node is from the root.
Root is assumed to be level 0.

5. Binary Tree
7 / 1 7 / 2 0 2 1
5
The simplest form of tree is a binary tree. A binary tree consists of a node (called
the root node) and left and right sub-trees. Both the sub-trees are themselves
binary trees.
Binary tree is a set of finite nodes which is either empty or consists of one or
more nodes in which each node has at most two disjoint binary sub trees called
left sub tree or right sub tree respectively.
There may be a zero degree node or a one degree node or a two degree node.

6. Binary Tree
7 / 1 7 / 2 0 2 1
6

7. Strictly Binary Tree
7 / 1 7 / 2 0 2 1
7
A binary tree is strictly binary tree if every
non-terminal node has two sub trees or you can say
if every non-terminal node consists of non-empty
left sub tree as well as non-empty right sub tree.

8. Complete Binary Tree
7 / 1 7 / 2 0 2 1
8
Complete binary tree is a strict binary tree with all leaf nodes at the
same level. The number of nodes at level ‘n’ is 2 n-1

9. Properties of binary tree
7 / 1 7 / 2 0 2 1
9
 The maximum number of nodes at a level I of binary tree is 2I where I>=0.
 If h = height of a binary tree,
maximum number of nodes possible in a binary tree of height h is 2h-1
minimum number of nodes possible in a binary tree of height h is h
 For any non empty tree, number of terminal or leaf nodes is equal to number
of non terminal nodes (internal nodes) +1.
 For any non empty binary tree, if ‘n’ is the number of nodes and ‘e’ is the
number of edges, then n=e+1;

10. 7 / 1 7 / 2 0 2 1
10
Traversals of a Binary Tree
PREORDER TRAVERSAL:
 Process the root R.
 Traverse the left sub tree of R in preorder.
 Traverse the right sub tree of R in preorder.
INORDER TRAVERSAL:
 Traverse the left sub tree of R in inorder.
 Process the root R.
 Traverse the right sub tree of R in inorder.
POSTORDER TRAVERSAL:
 Traverse the left sub tree of R in postorder.
 Traverse the right sub tree of R in postorder.
 Process the root R.

11. Traversal - Example
7 / 1 7 / 2 0 2 1
11
INORDER TRAVERSAL: 10, 15, 16, 32, 33, 34, 87
PREORDER TRAVERSAL: 32, 16, 10, 15,34,33,87
POSTORDER TRAVERSAL: 15, 10, 16, 33, 87, 34, 32

12. 7 / 1 7 / 2 0 2 1
12
The inorder and preorder traversals of a binary tree are as follows
Inorder: MOUPTCRES
Preorder: COMPUTERS
Draw the binary tree and write the postorder traversal.

13. Graph Traversals
7 / 1 7 / 2 0 2 1
13
A graph traversal means visiting the nodes of a graph one after the other in a
systematic manner .Two important graph traversals techniques are
1. Breadth First Search (BFS)
2. Depth First Search(DFS)

14. BFS (Breadth First Search)
7 / 1 7 / 2 0 2 1
14
In graphs we do not have any special vertex designated as source vertex. So
traversal can start from any arbitrary vertex. So traversal can start from any
arbitrary vertex.
Each vertex in a graph has an associated level which arises from the position of
that vertex in the graph.
If the traversal is starting from the node A, we examine the node A then we visit
all the neighbours of A.
Then we examine all the neighbours of the neighbours of A and so on. In BFS
the vertices are visited in the order of their levels.
At each level, the vertices are visited from left to right.

15. BFS (Breadth First Search)-Design
7 / 1 7 / 2 0 2 1
15
Since the vertices are visited from level 0, level 1and so on, we can
implement BFS using queue data structure. To begin with insert the source
vertex into the queue, and then repeat the following steps until queue is
empty.
1. Delete a vertex from the queue and the vertex is visited or processed.
2. All the nodes which are adjacent to the deleted vertex but not visited
earlier are inserted into the queue from left to right.

16. 7 / 1 7 / 2 0 2 1
16
ALGORITHM BFS(v)
/* Let v be the starting vertex
visited[i] = false initially for i = 1 to n
for any node i visited [i] = true if i has already been visited else it contains false.
Queue is represented as q */
{
u=v;
visited[v]=true;
repeat
{ for all vertices w adjacent from u do
{ if ( visited [w]==false) then
{ add vertex w to q;
visited [w] =true;
}
}
if q is empty then return ;
delete vertex u from q;
}until (false);
}

17. BFS (Breadth First Search)
7 / 1 7 / 2 0 2 1
17

18. BFS (Breadth First Search)
7 / 1 7 / 2 0 2 1
18

19. DFS (Depth First Search)
7 / 1 7 / 2 0 2 1
19
Traverses a single path of the graph as far as it can go (that is until it visits a
node with no successor or a node of all whose successors have already been
visited). It then resumes the last node on the path just traversed that has
unvisited successors and begins traversing a new path emanating from that
node.

20. DFS-Design
7 / 1 7 / 2 0 2 1
20
Stack is used to implement DFS.
Whenever a vertex is visited for the first time, that vertex is pushed on to
the stack and the vertex is deleted from the stack when a dead end is
reached and the search resumes from the vertex that is deleted most
recently .
If there are no vertices adjacent to the most recently deleted vertex, the
next node is deleted from the stack and the process is repeated until all the
vertices are reached or till the stack is empty.

21. 7 / 1 7 / 2 0 2 1
21
Algorithm depthfirst(vertex v)
{
visited [v] =true;
for each vertex w adjacent to i do
if (visited[w]==false)
depthfirst(w)
}
ALGORITHM DFS(v)
/* Let G be the given graph with n vertices.
{
for i = 1 to n
visited[i] = false
for i =1 to n
if ( visited [i]==false) then
depthfirst (i);
}

22. DFS-Example
7 / 1 7 / 2 0 2 1
22

23. DFS-Solution
7 / 1 7 / 2 0 2 1
23

24. Applications of DFS and BFS
7 / 1 7 / 2 0 2 1
24
1. To check whether the given graph is connected or not
2. To check whether the given graph is cyclic or not
3. To find the spanning tree
4. To find the vertices that is reachable from given vertex.