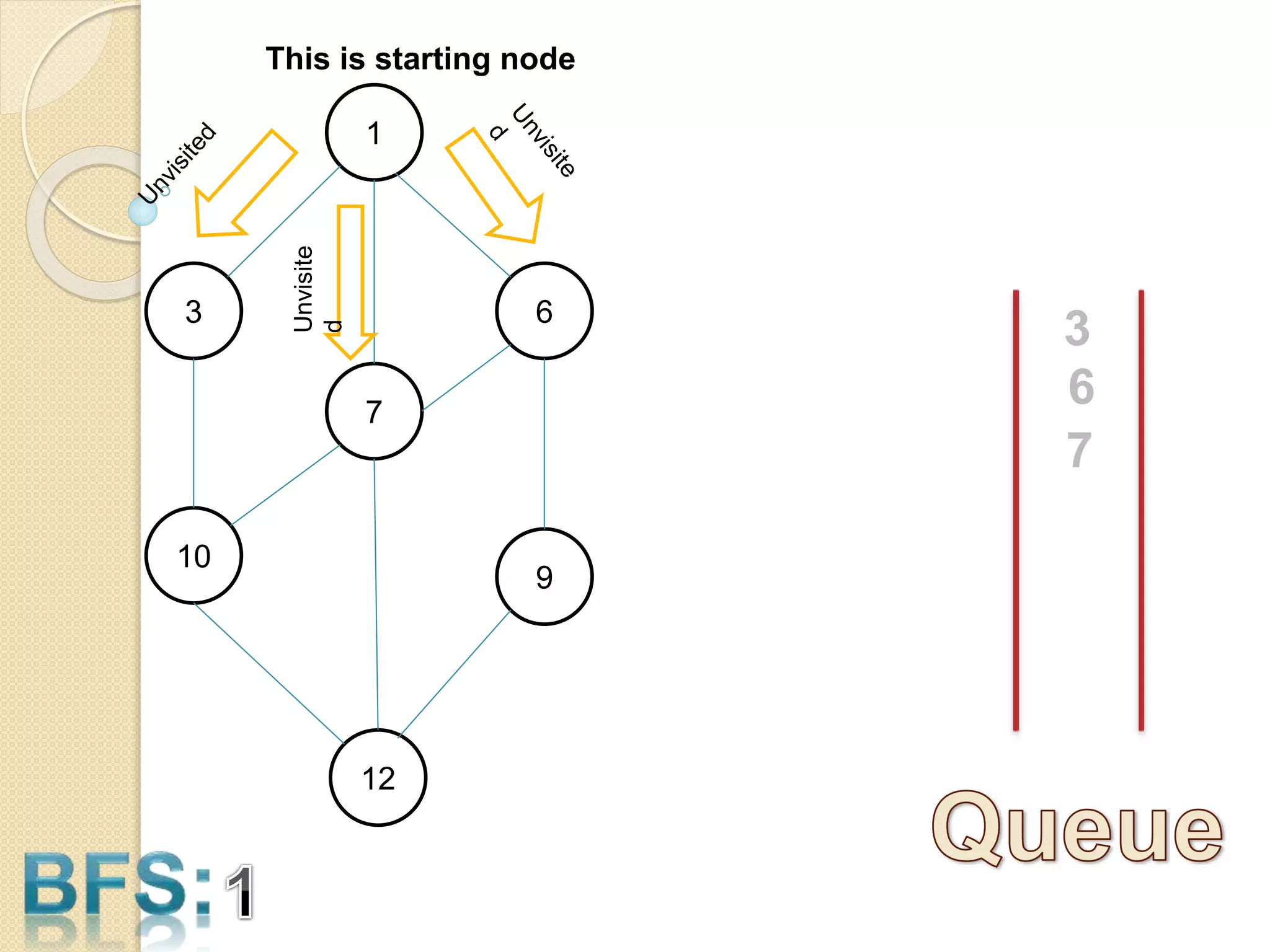
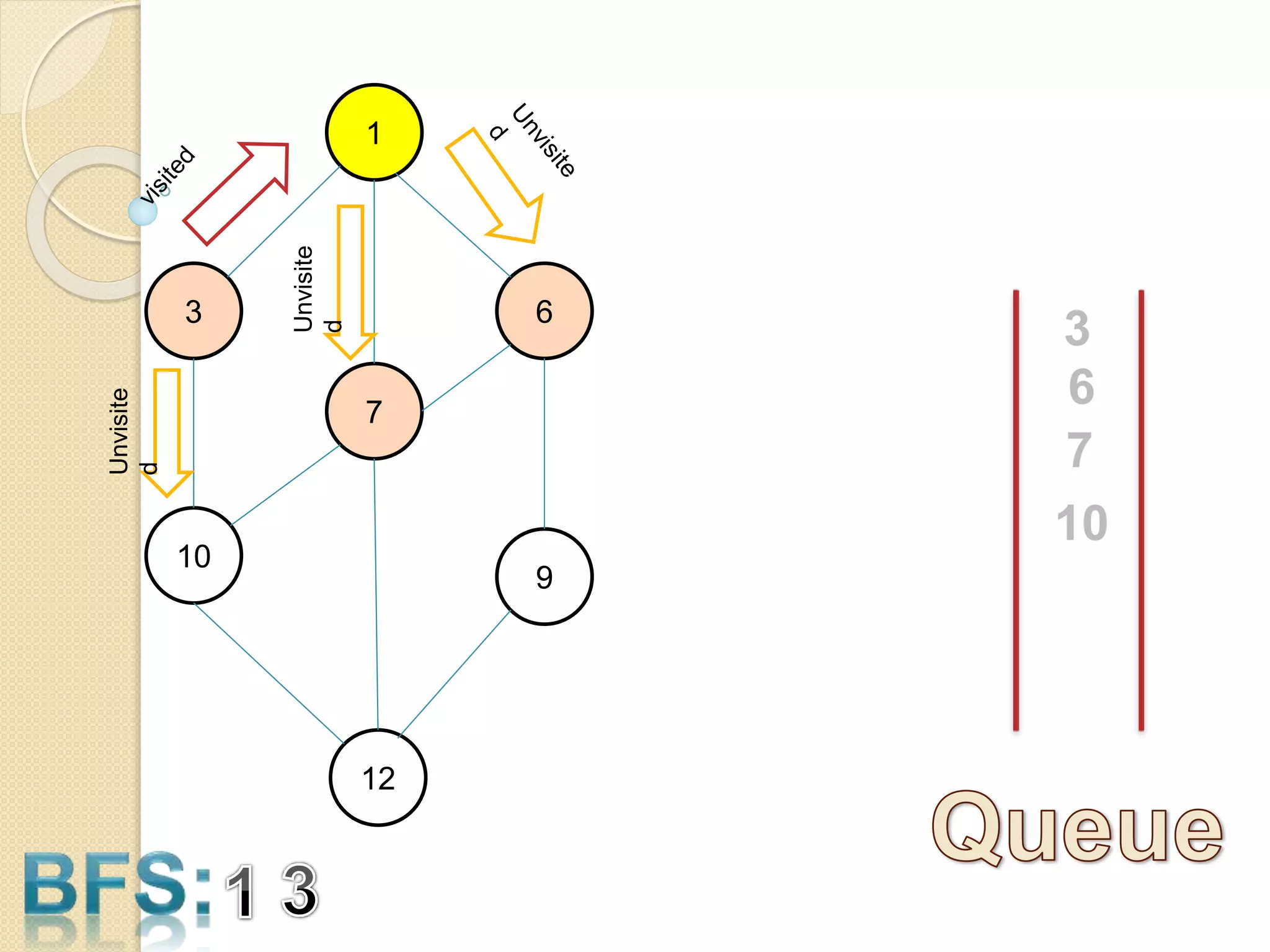
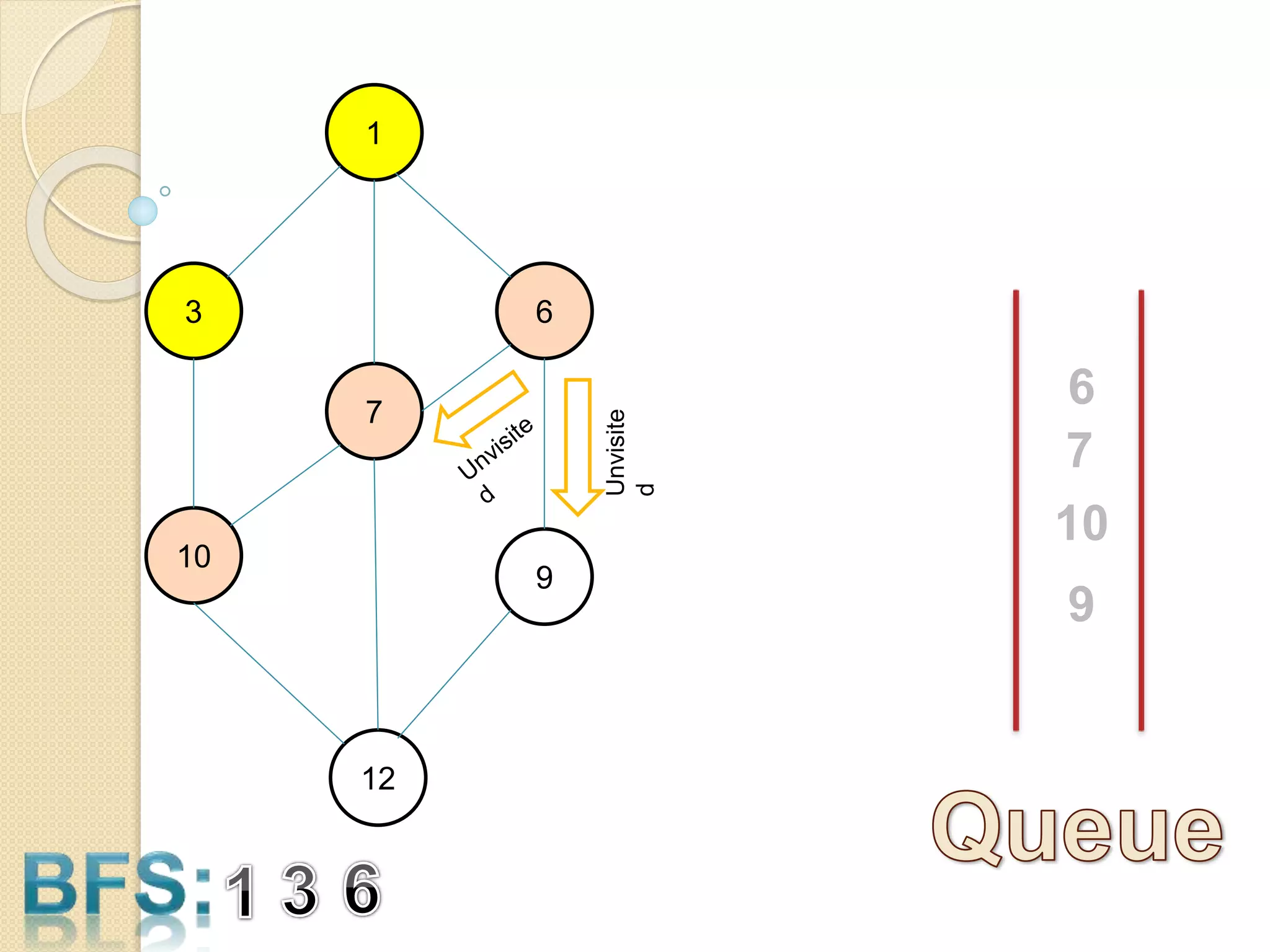
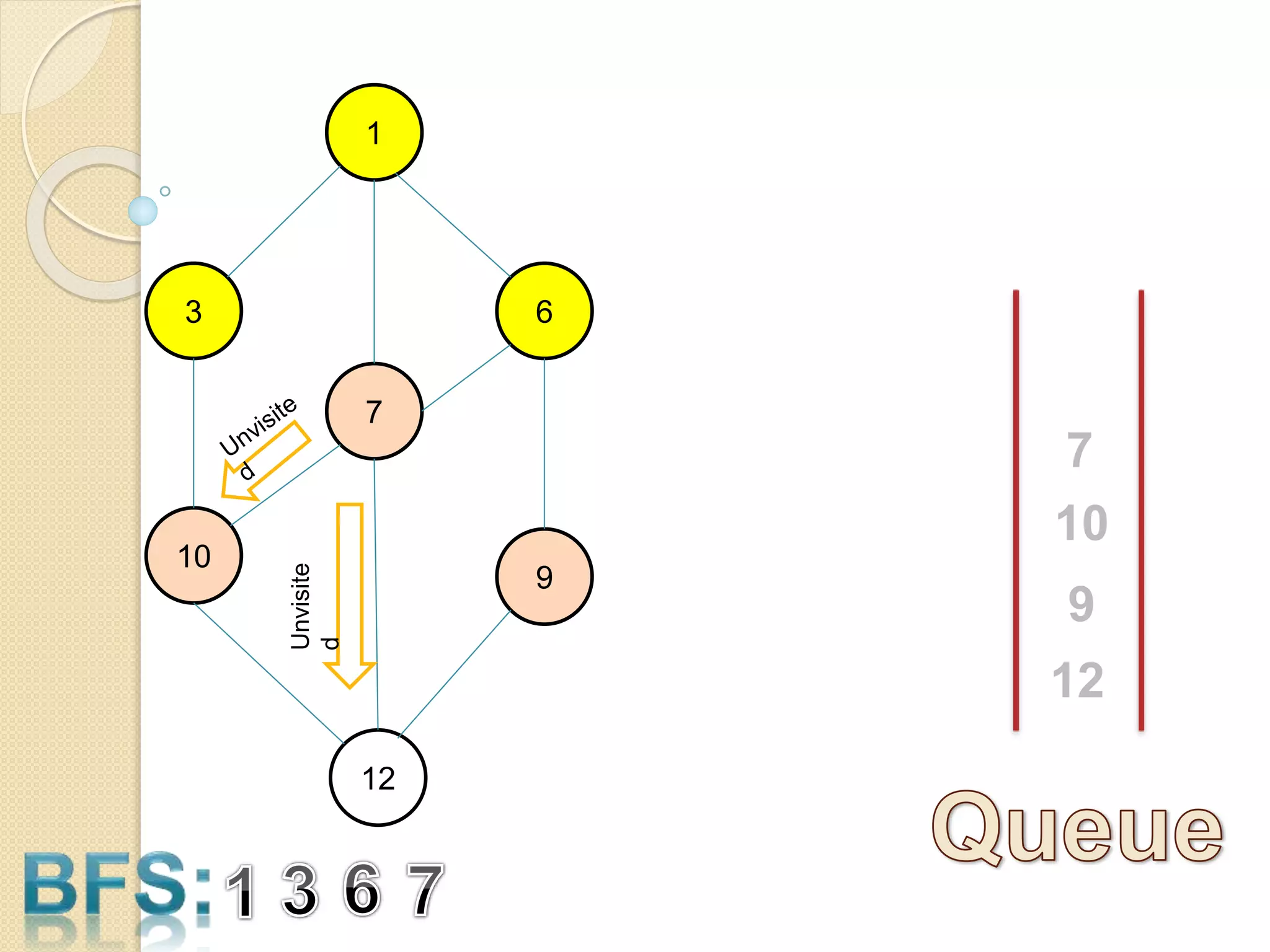
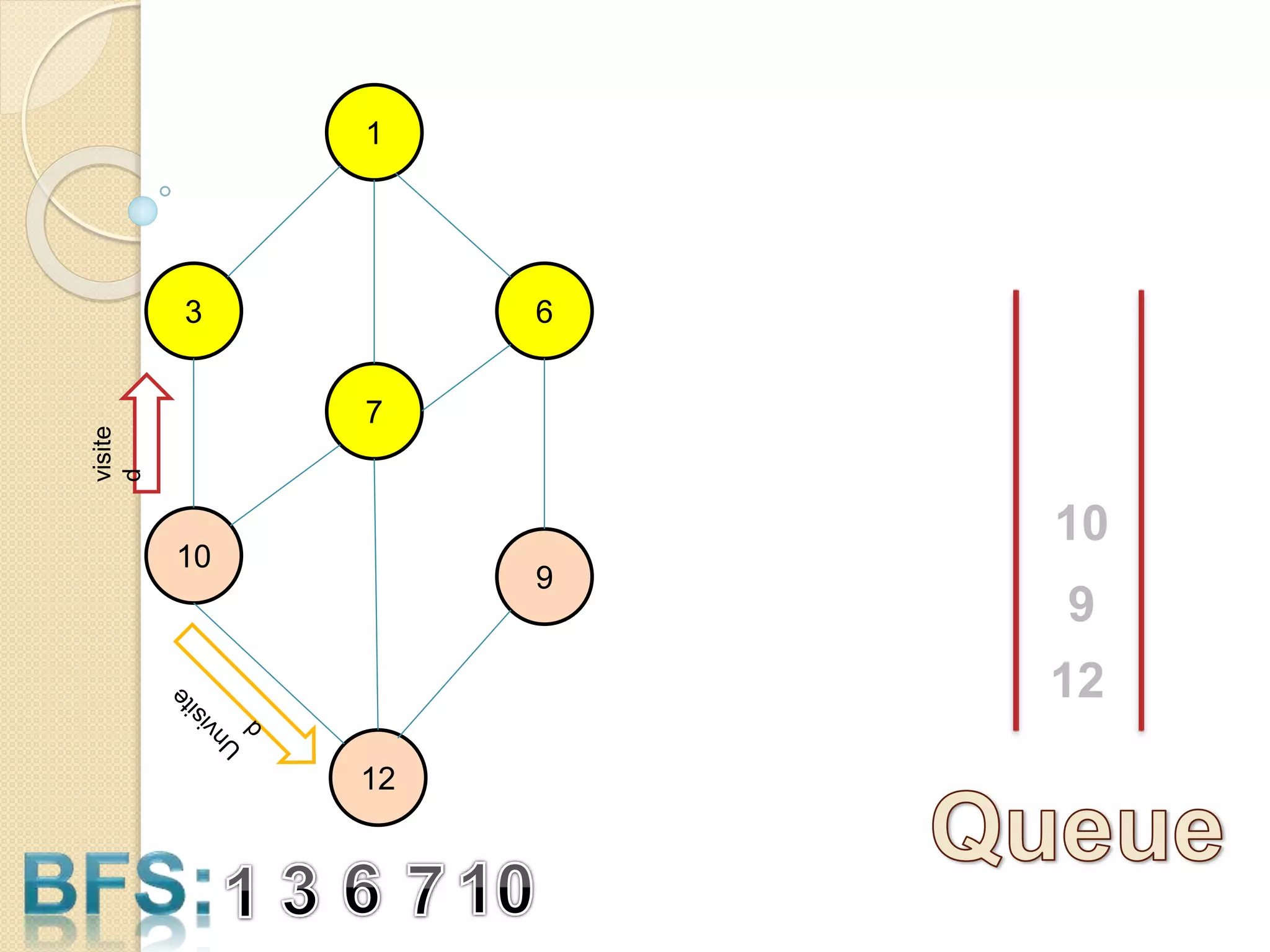
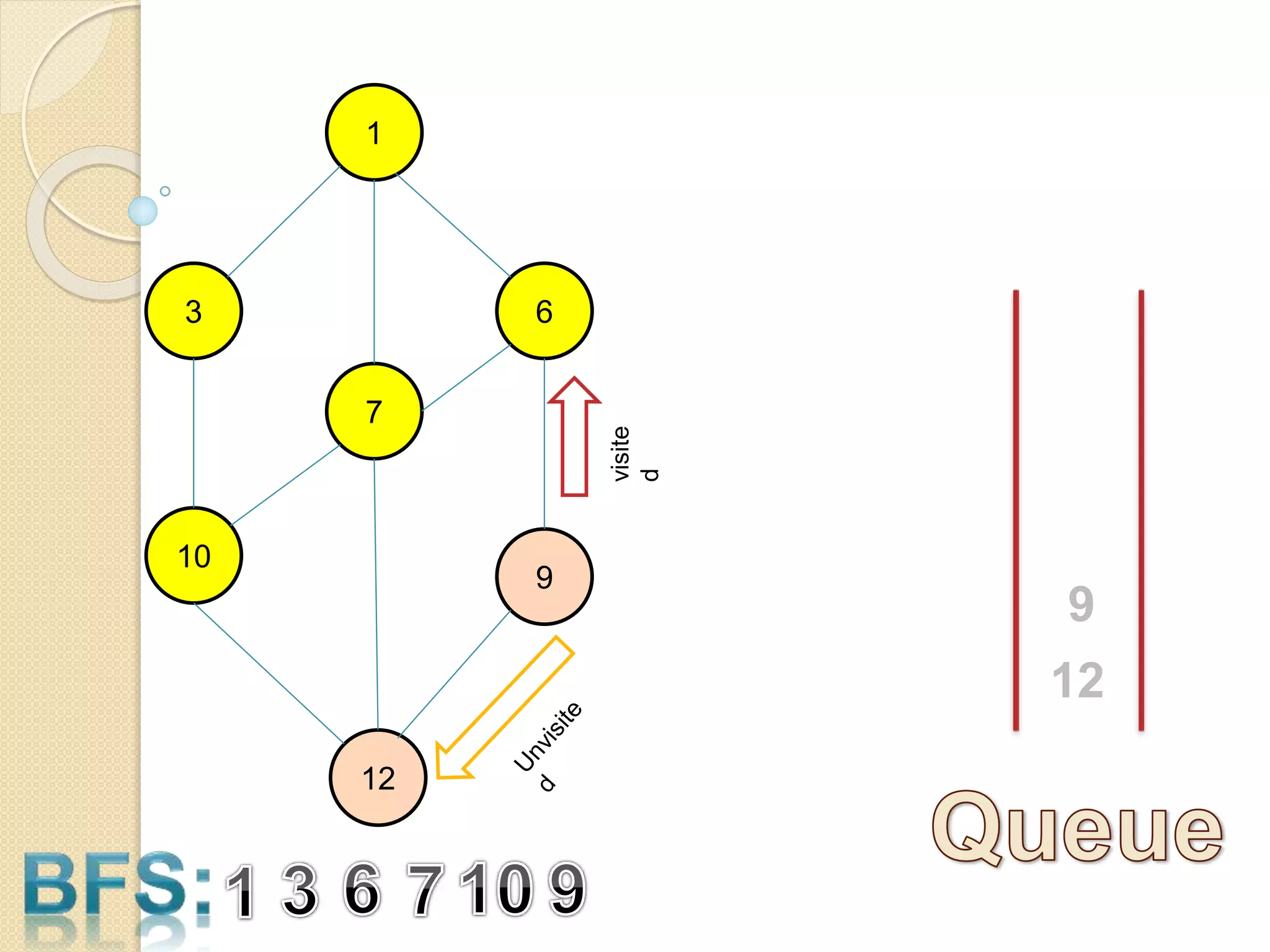
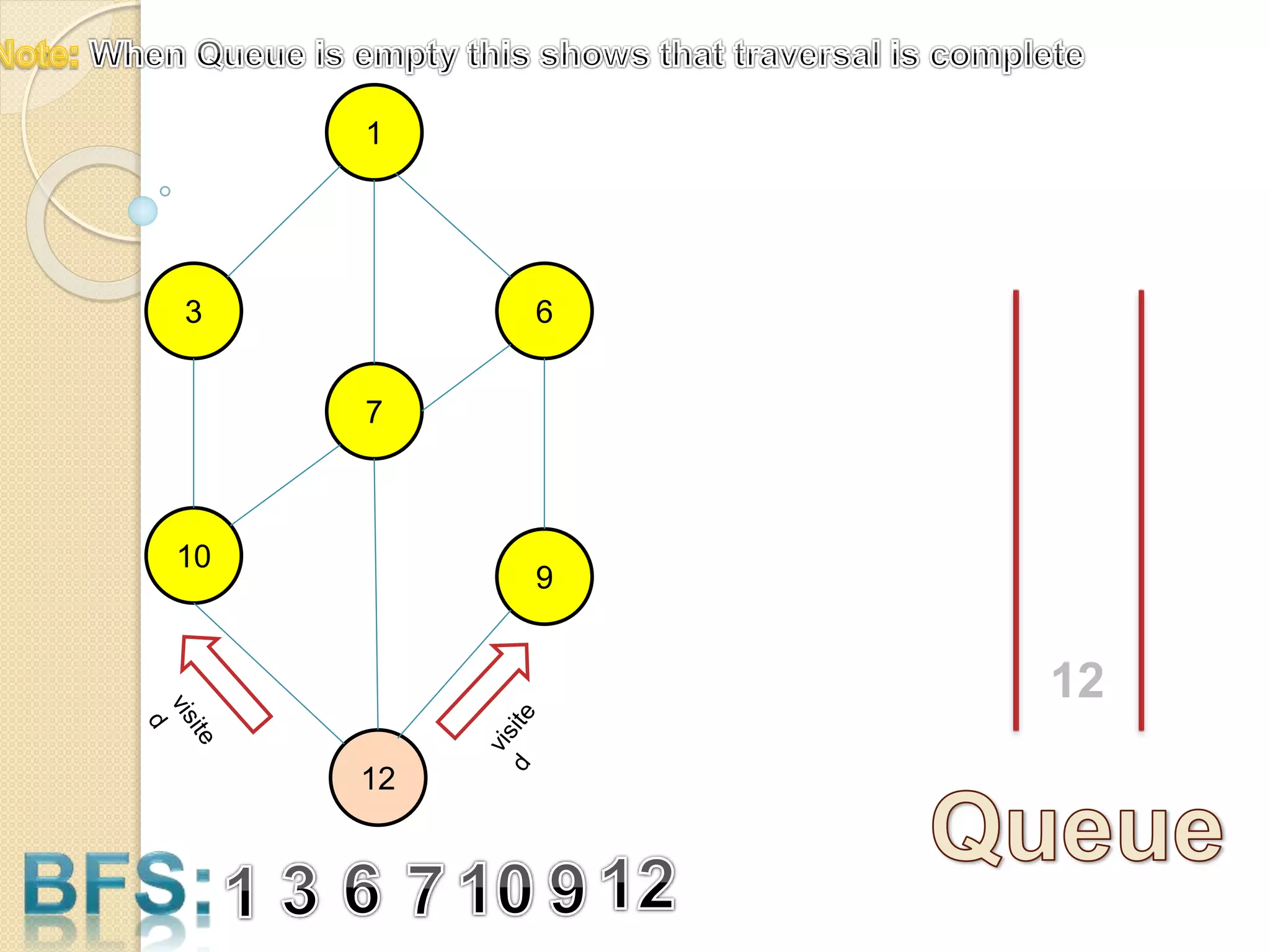
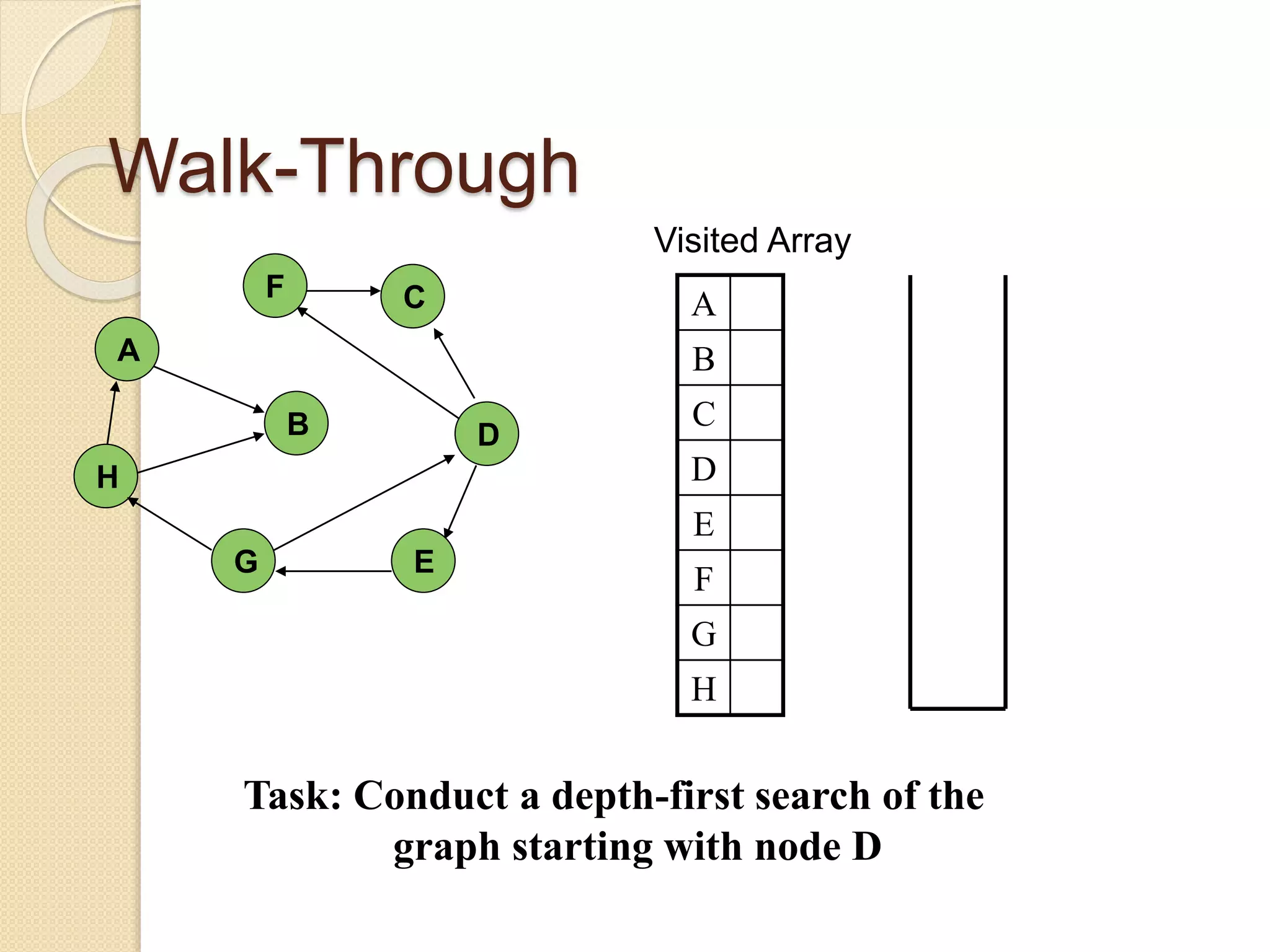
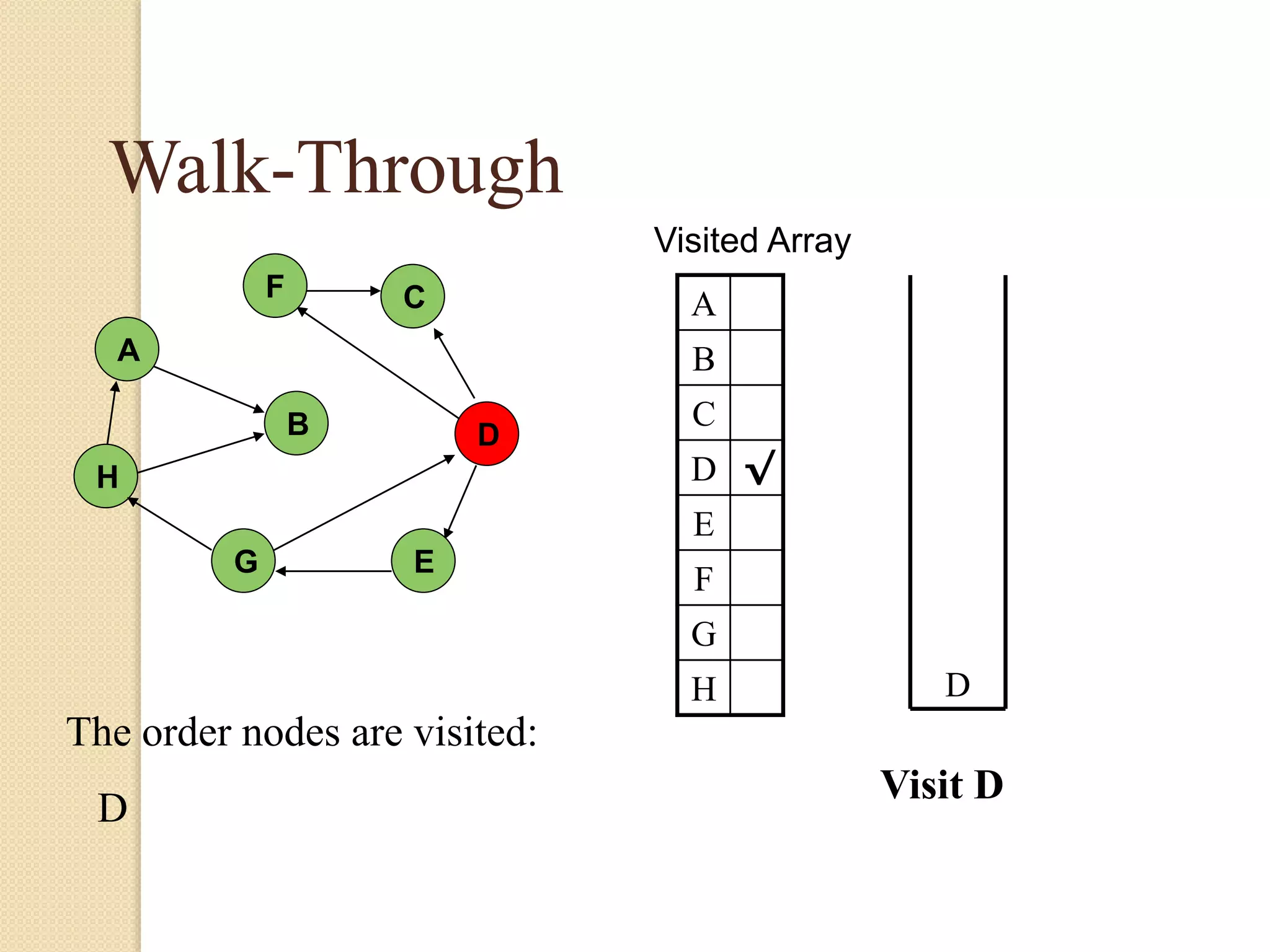
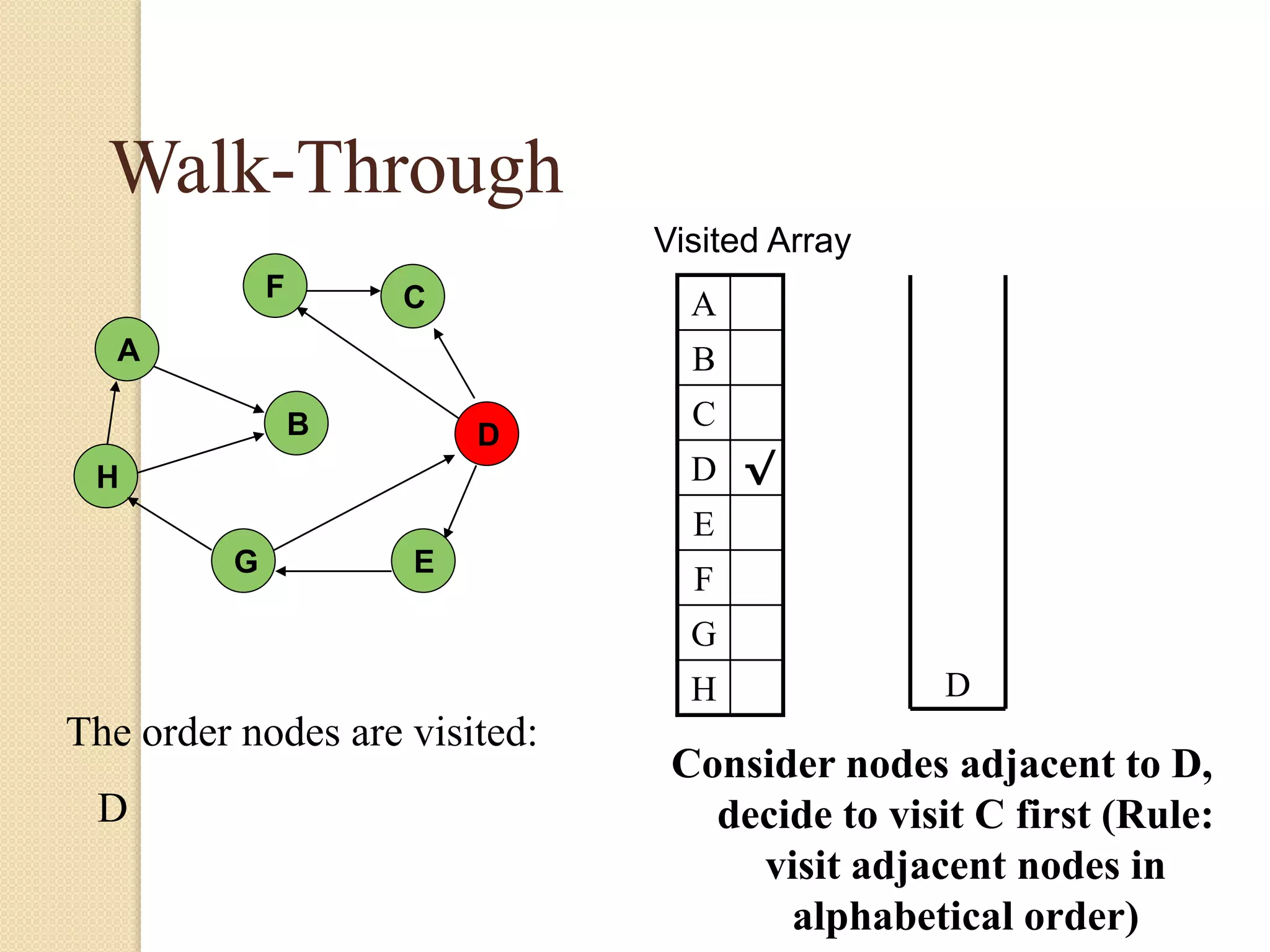
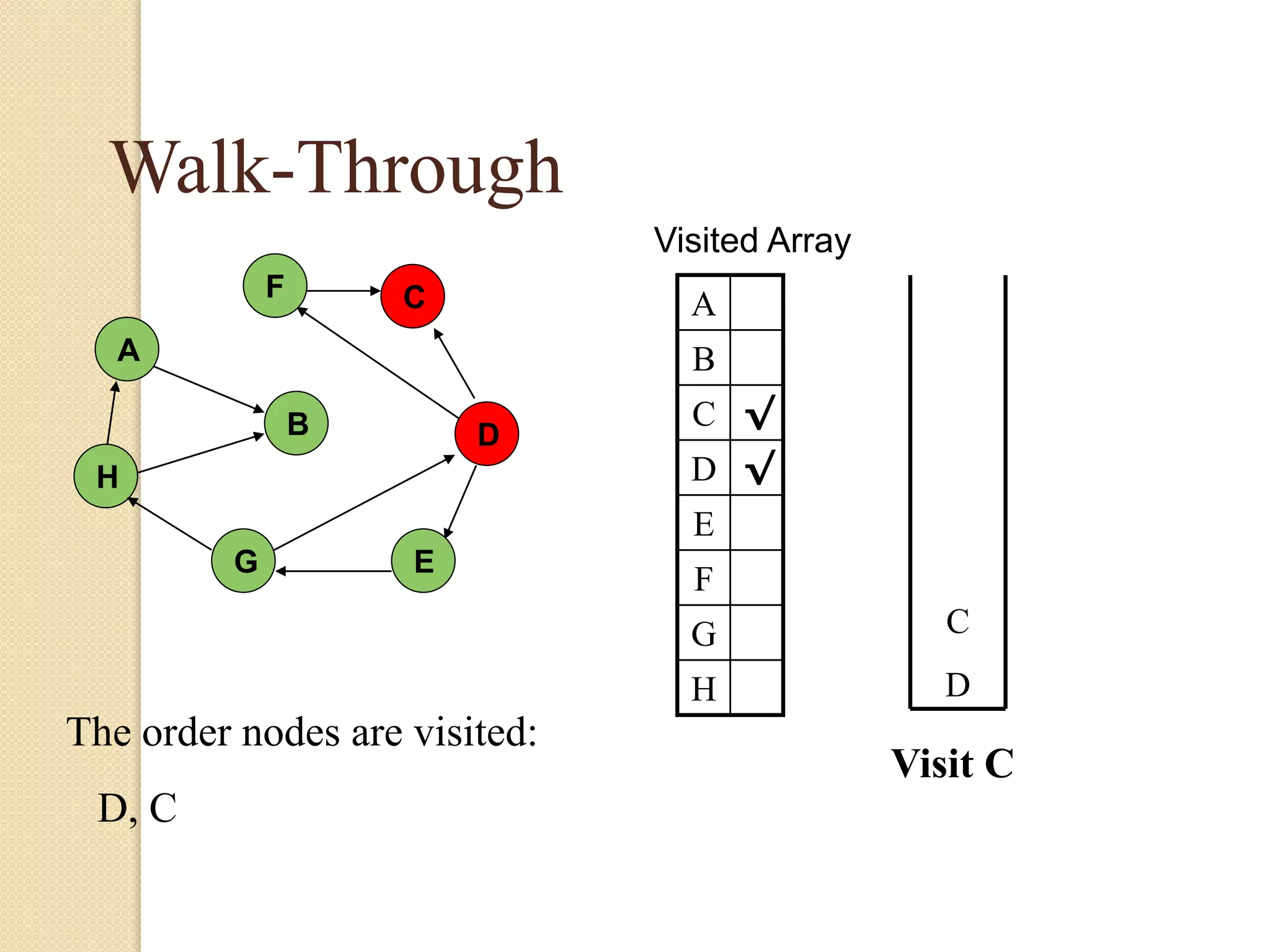
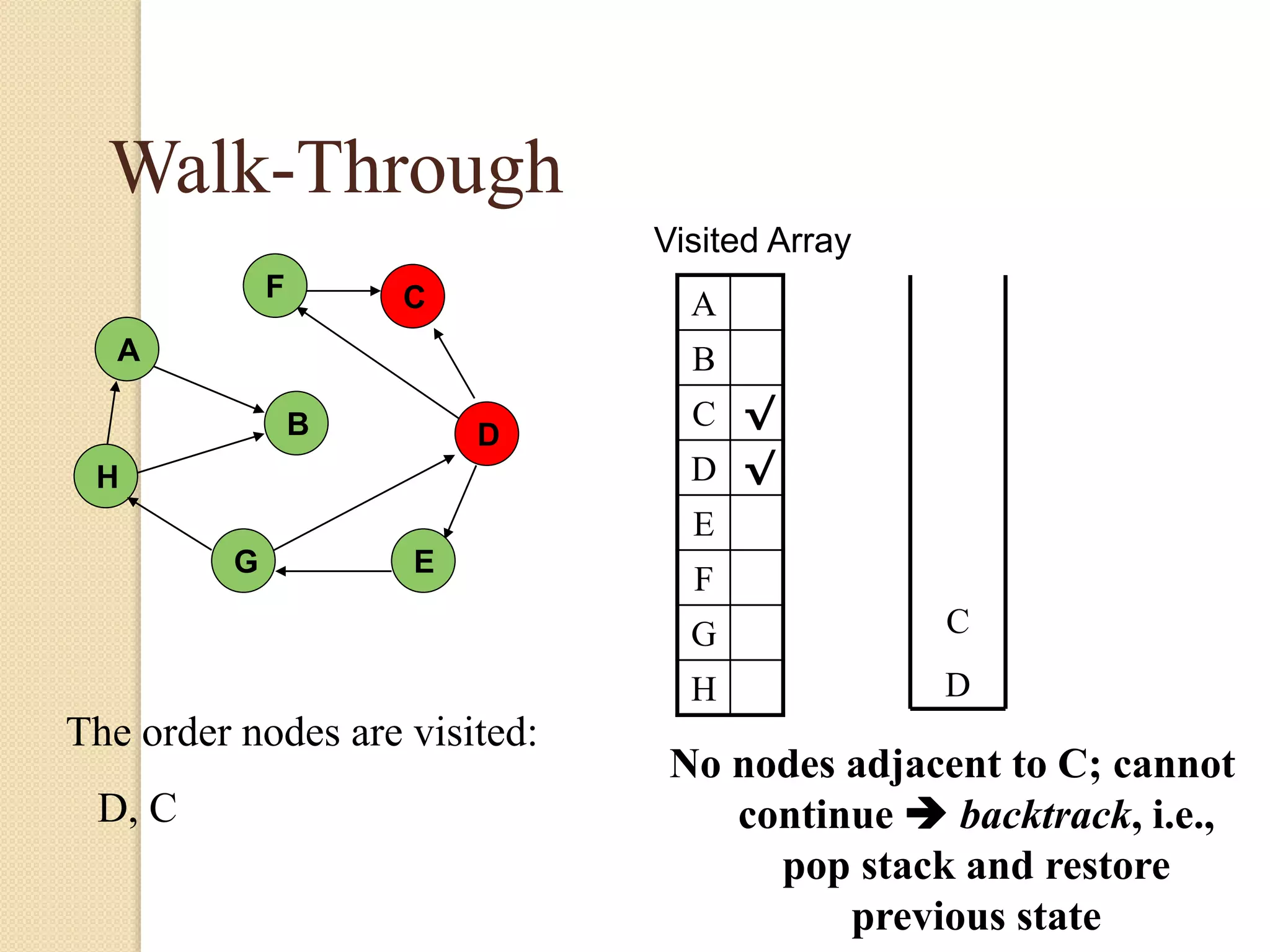
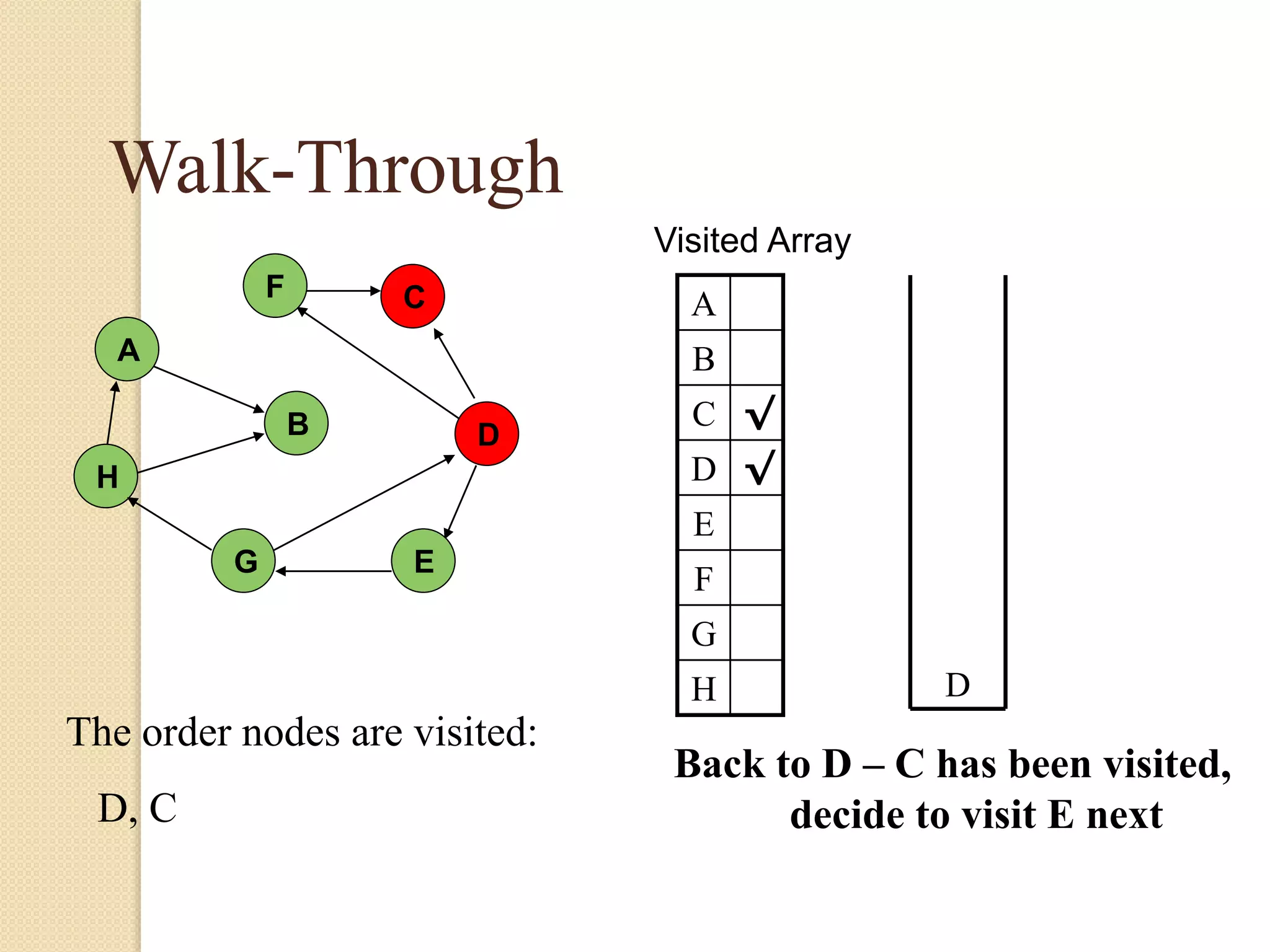
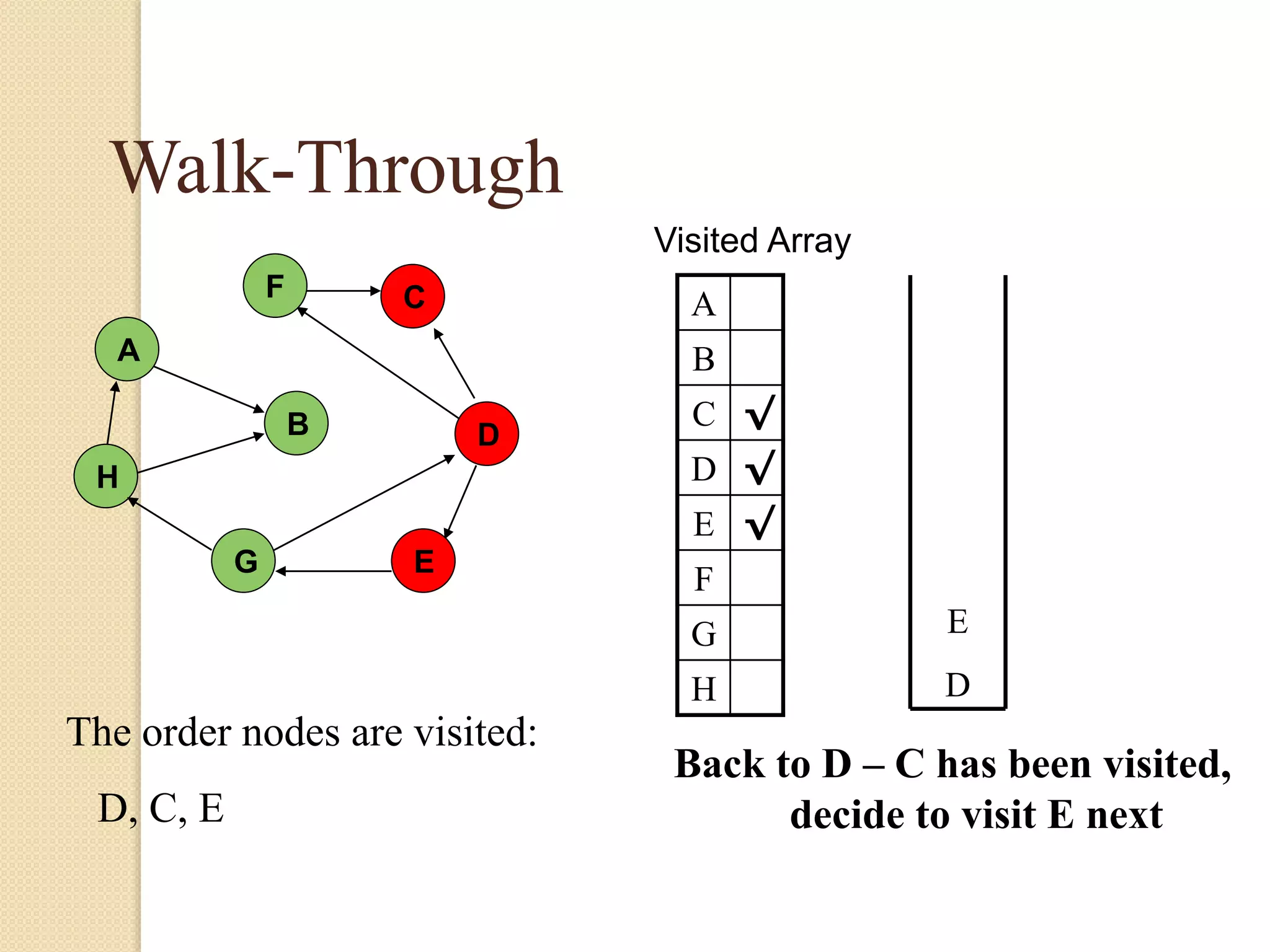
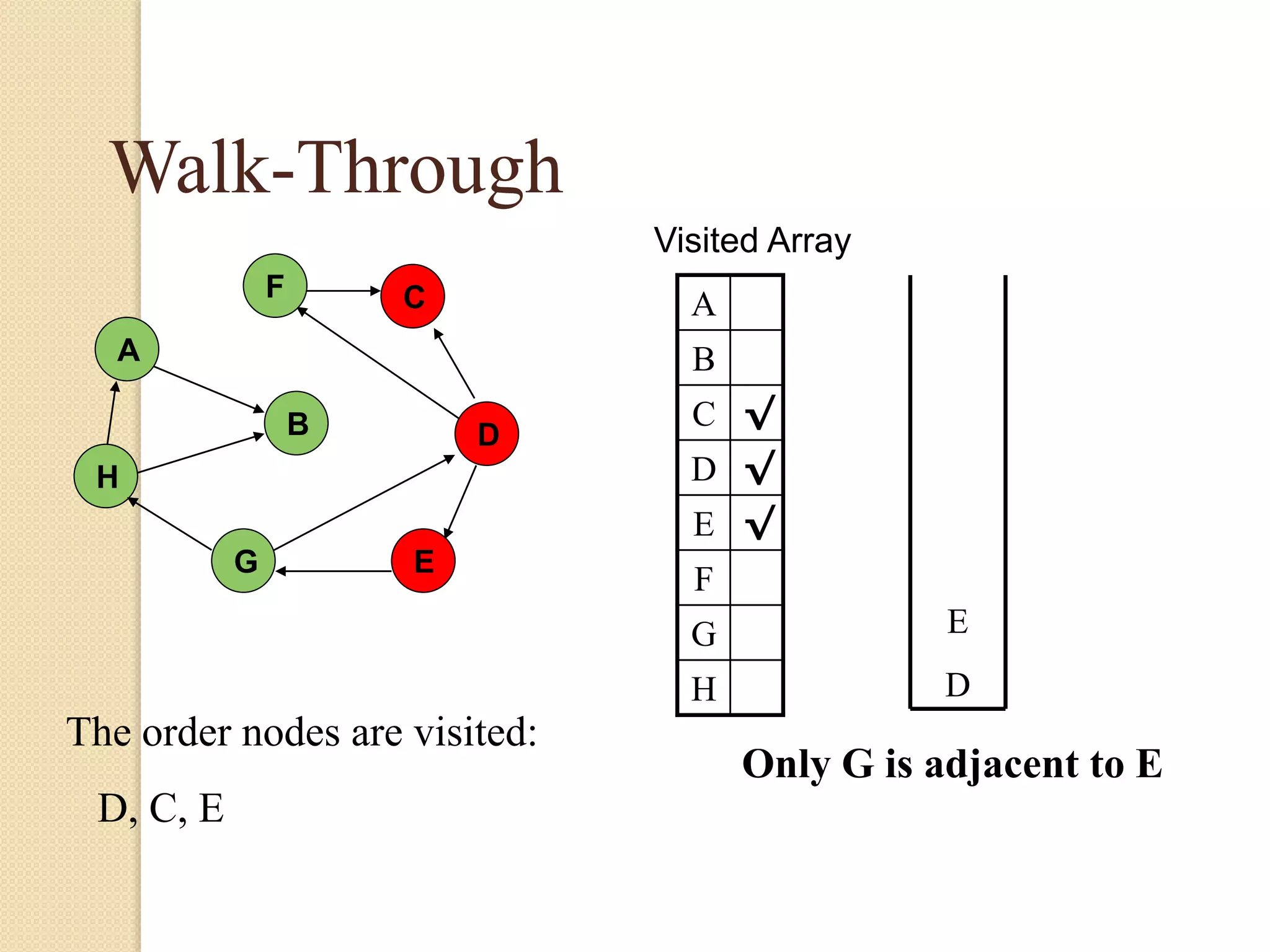
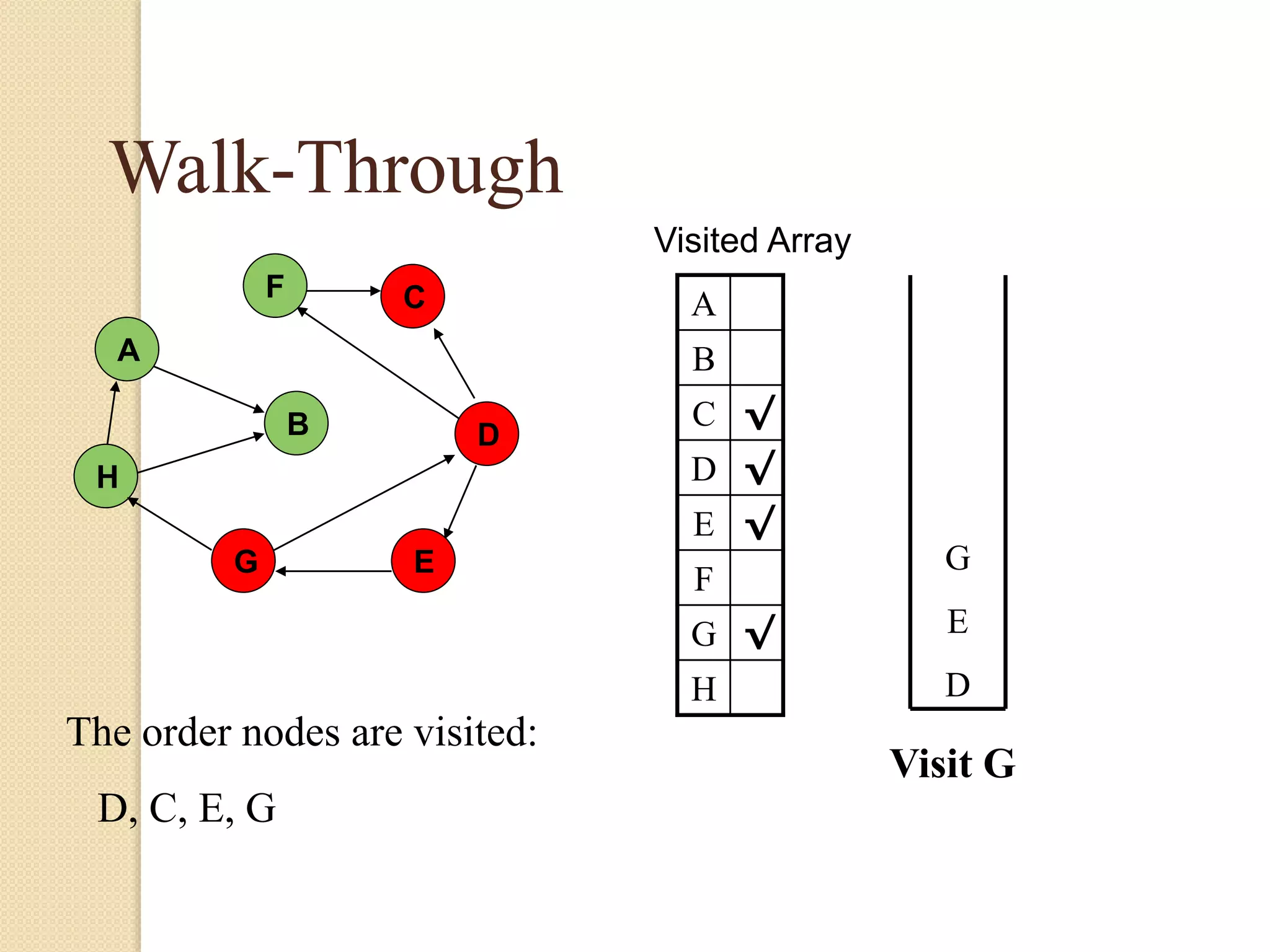
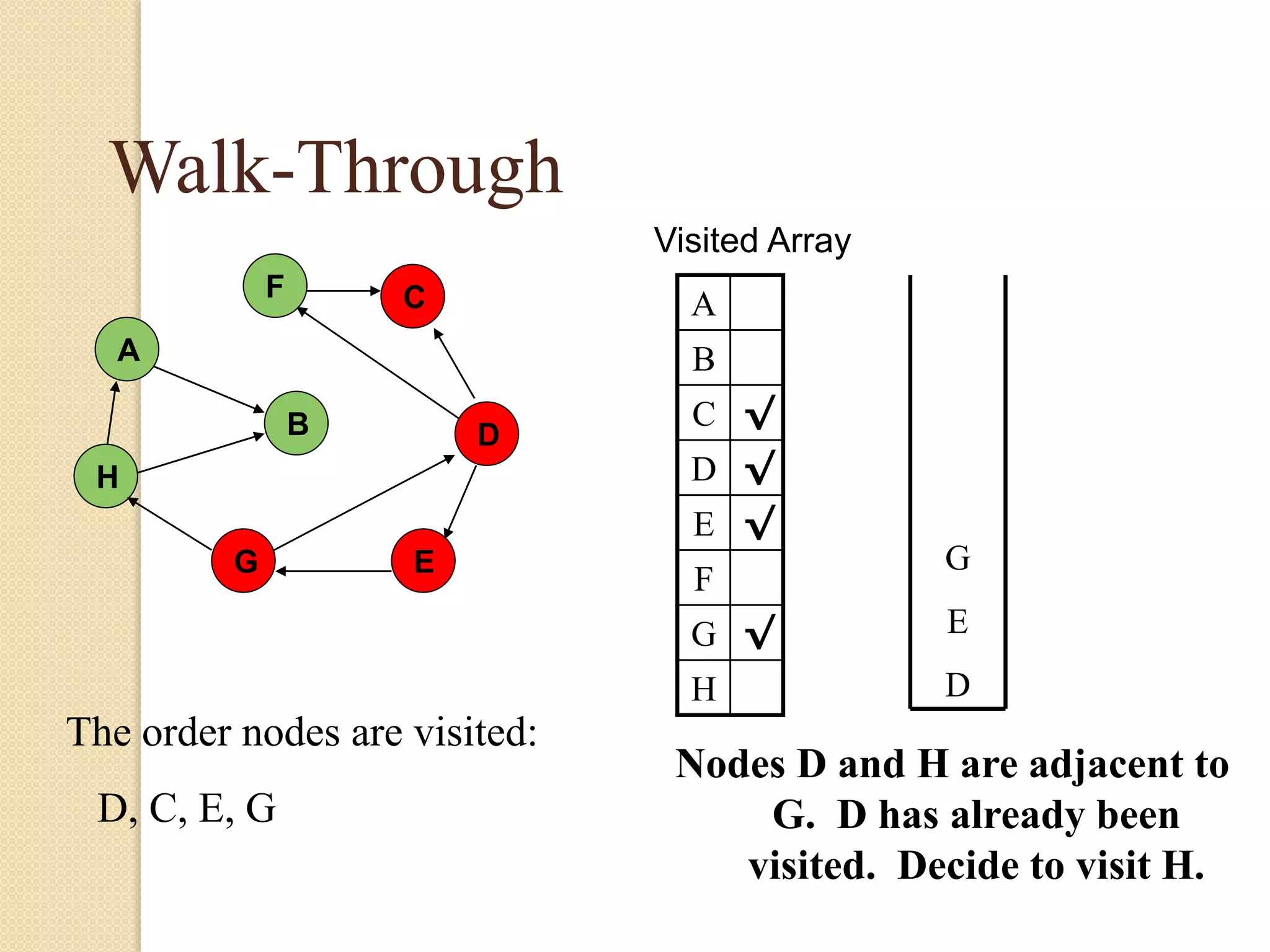
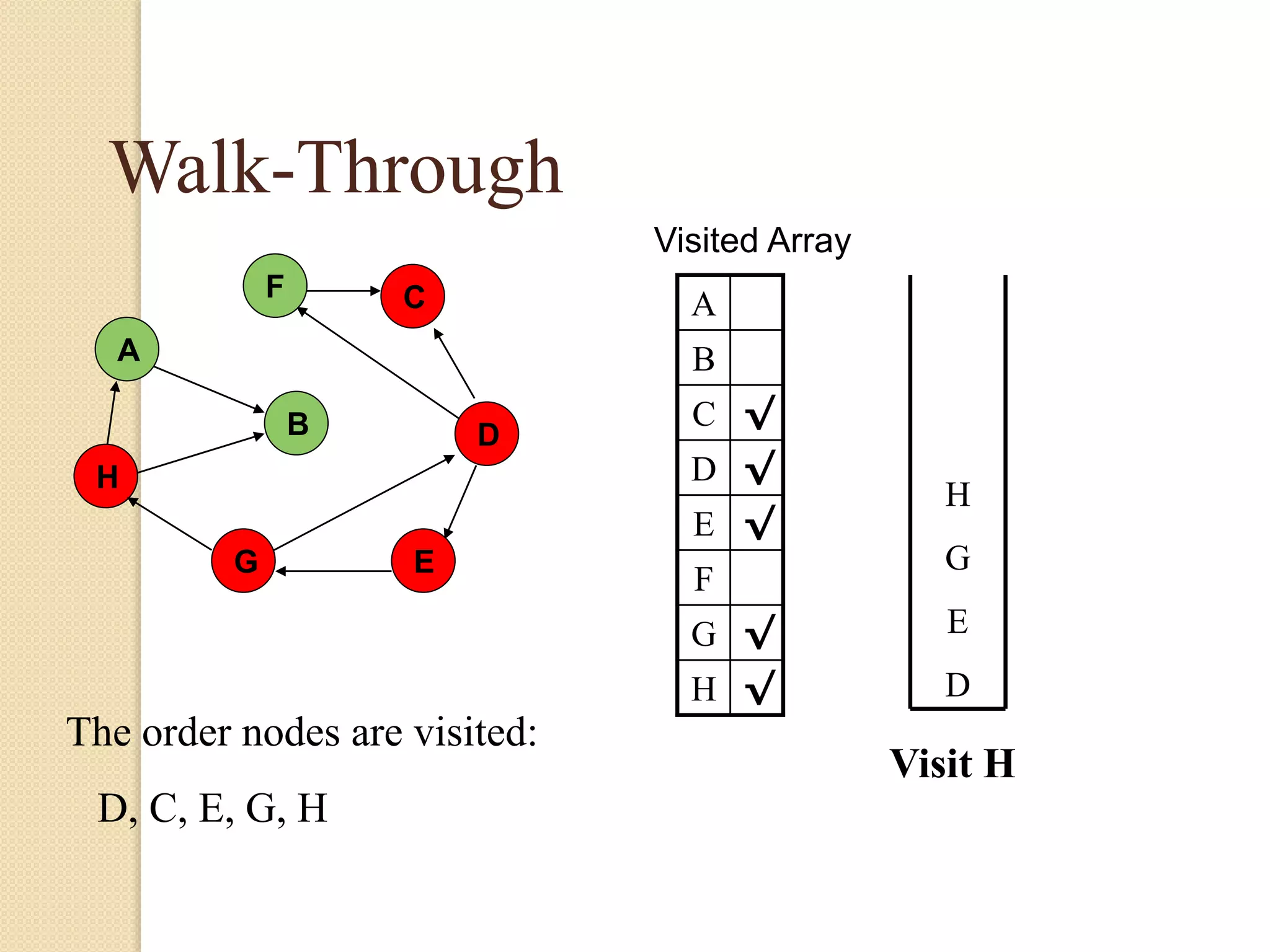
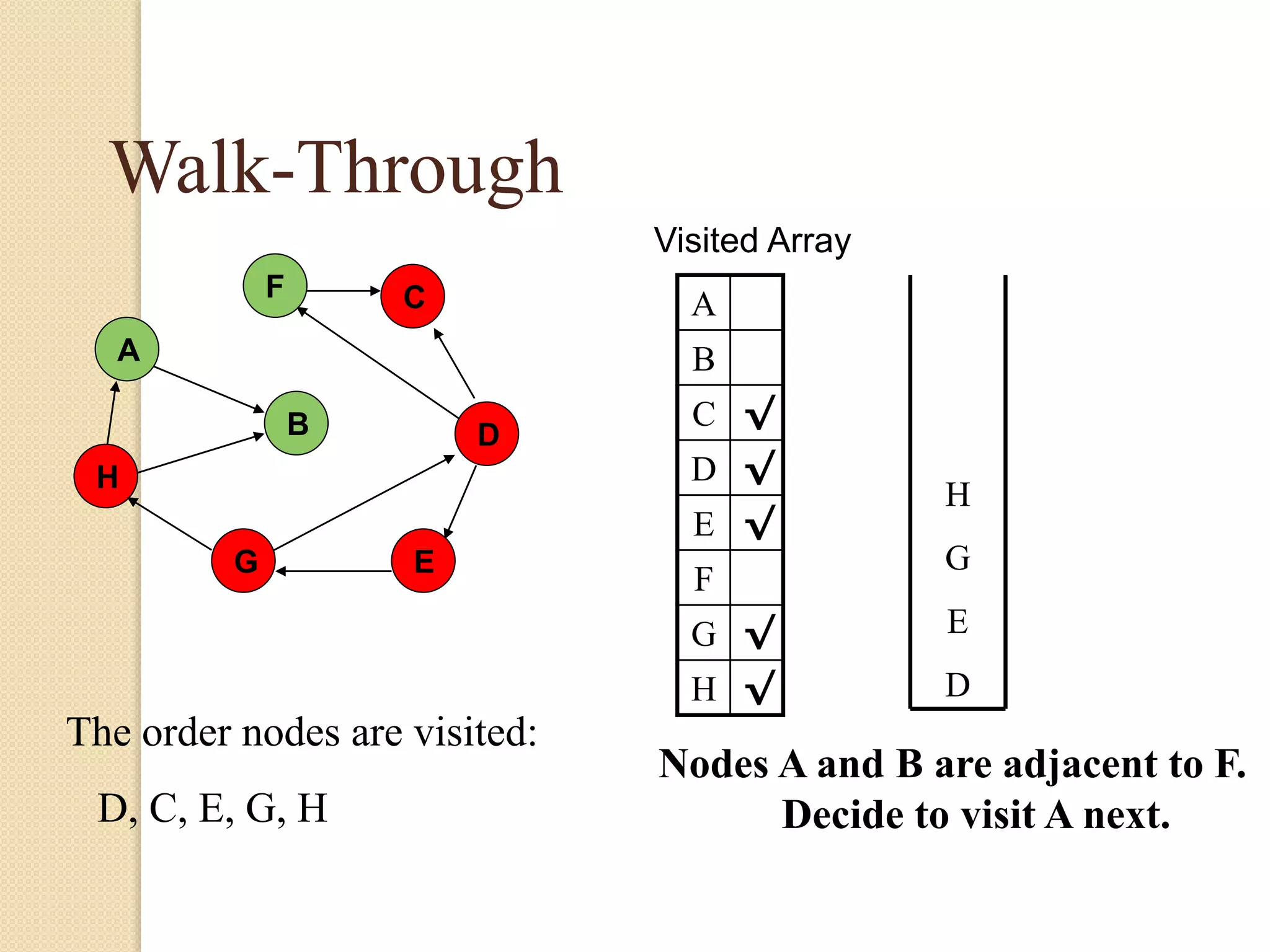
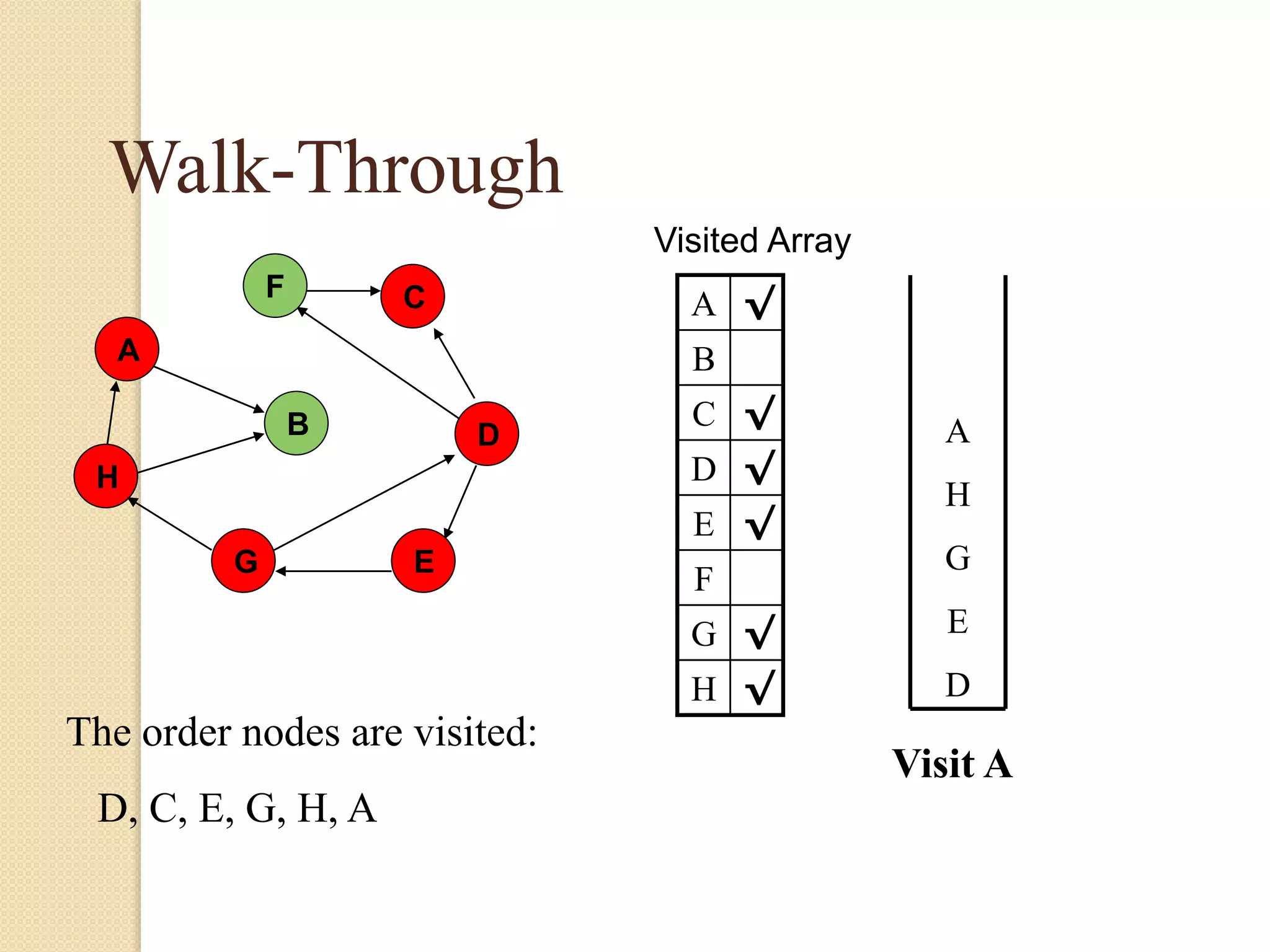
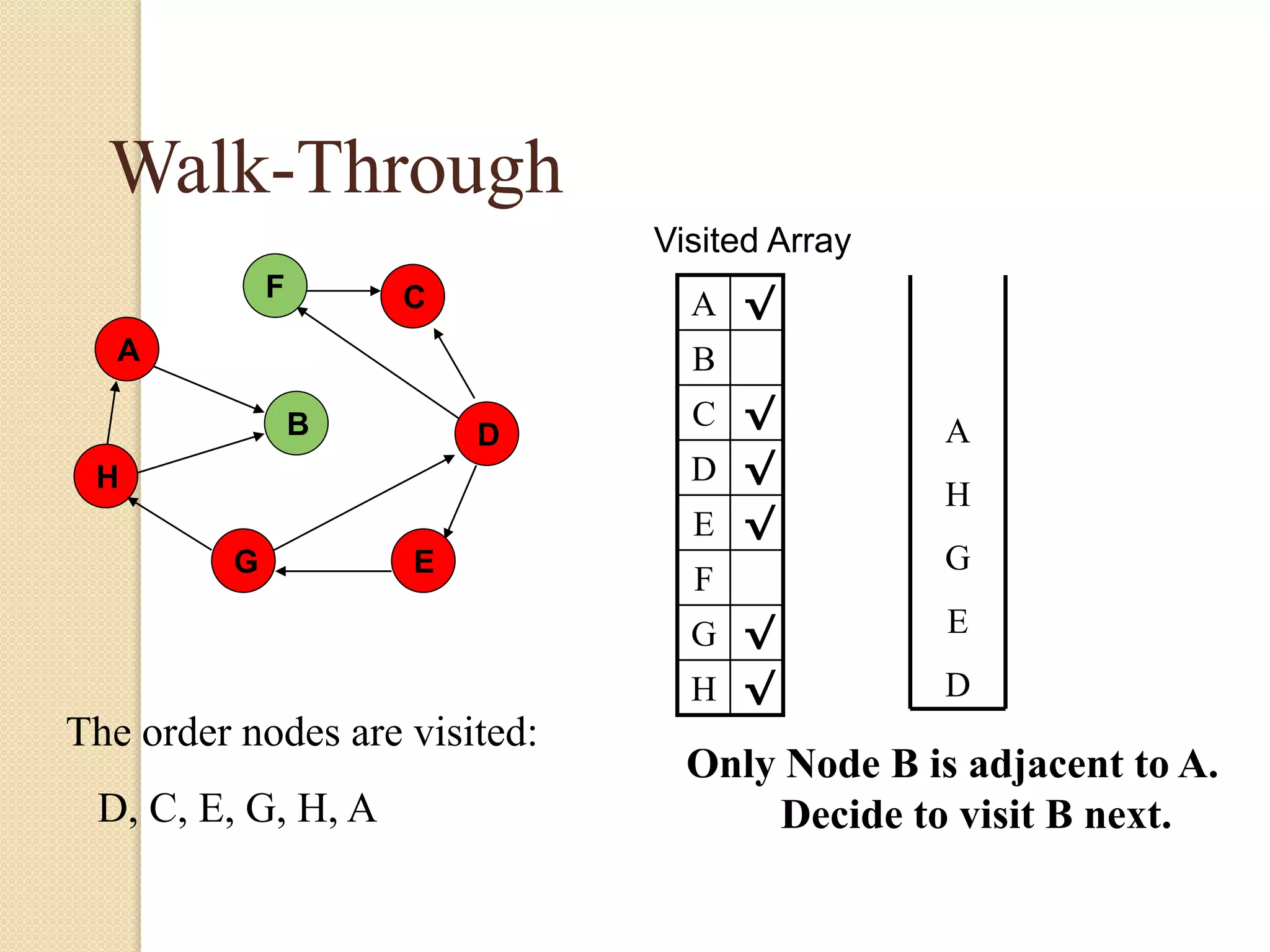
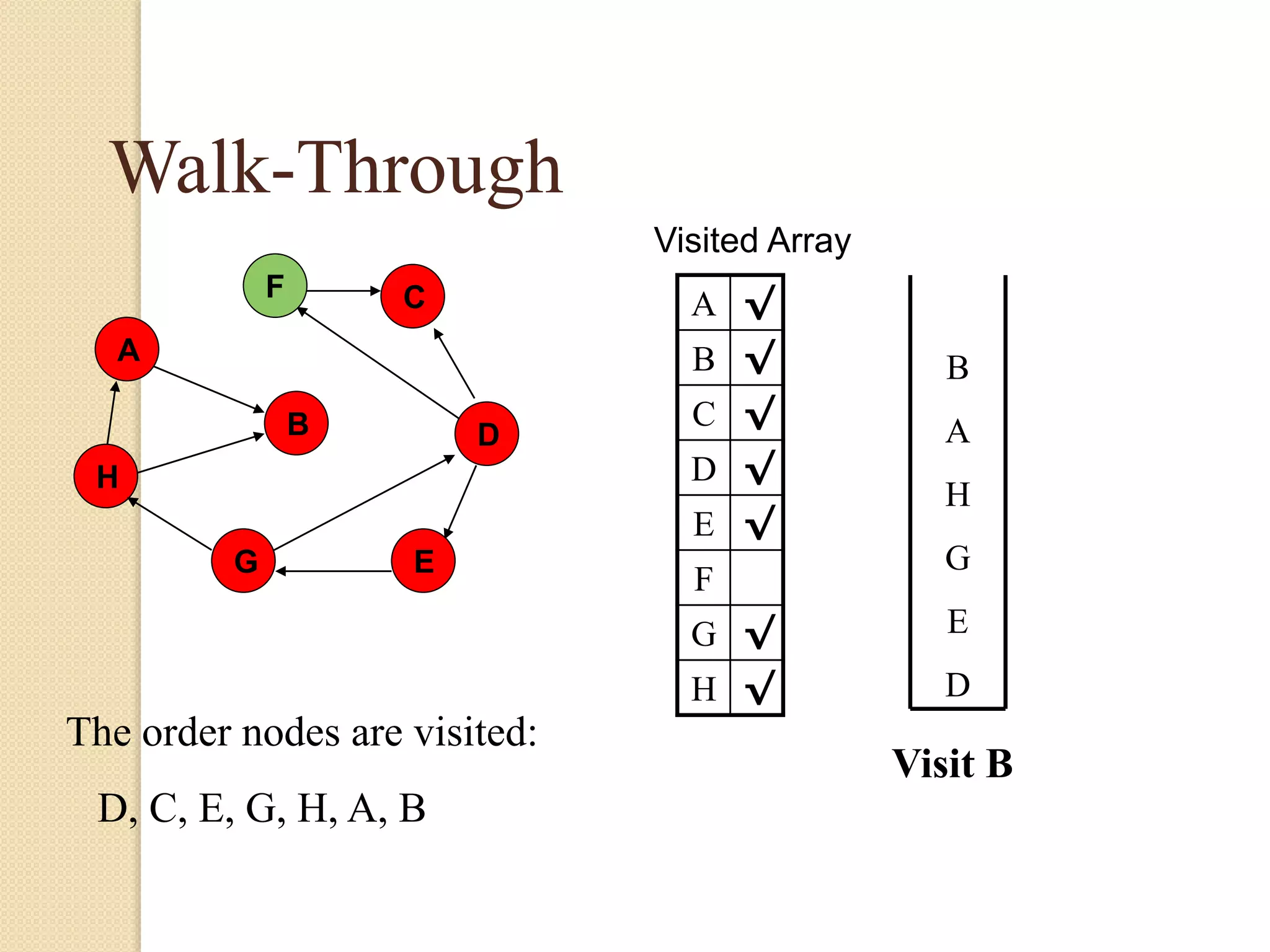
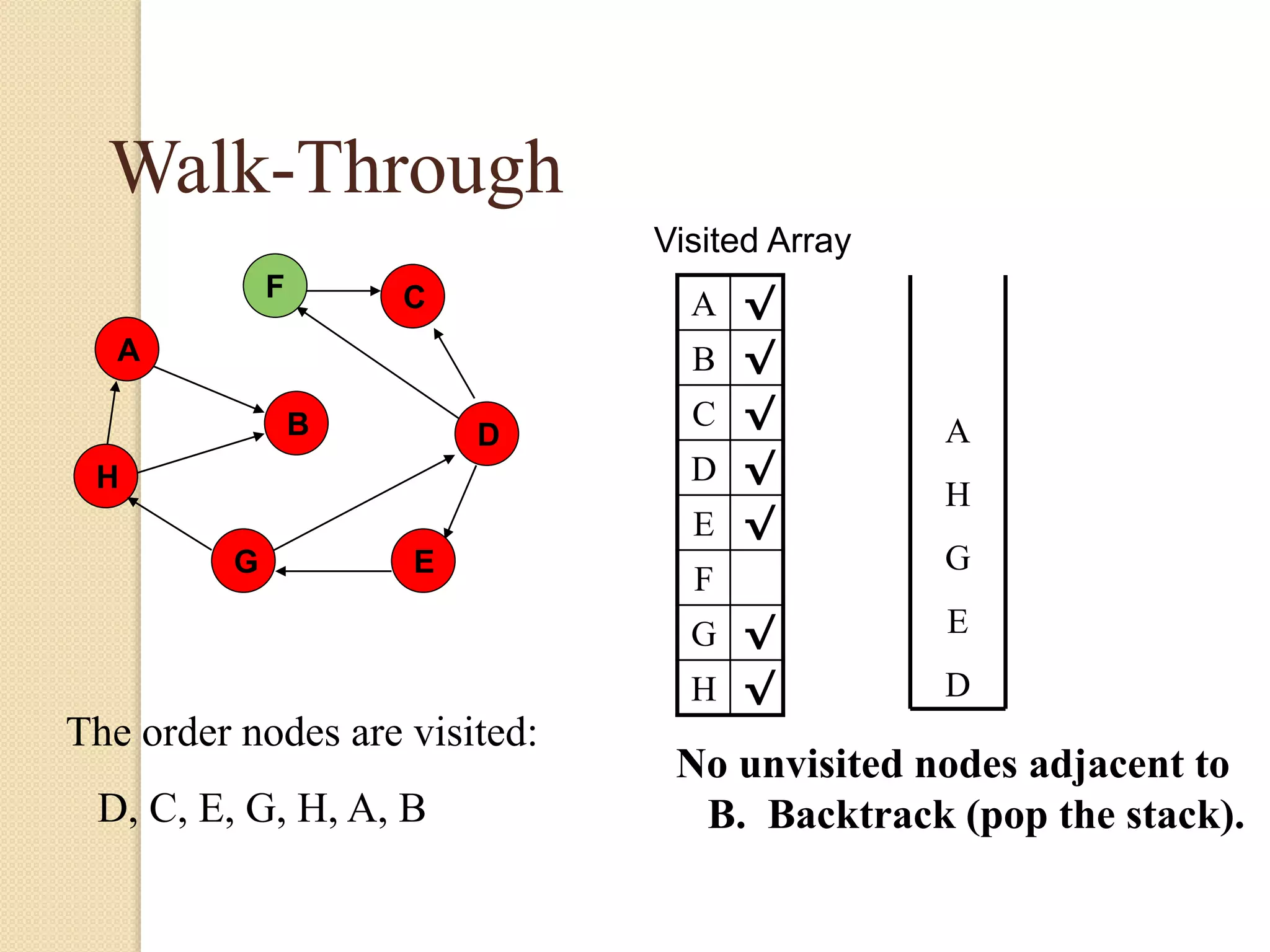
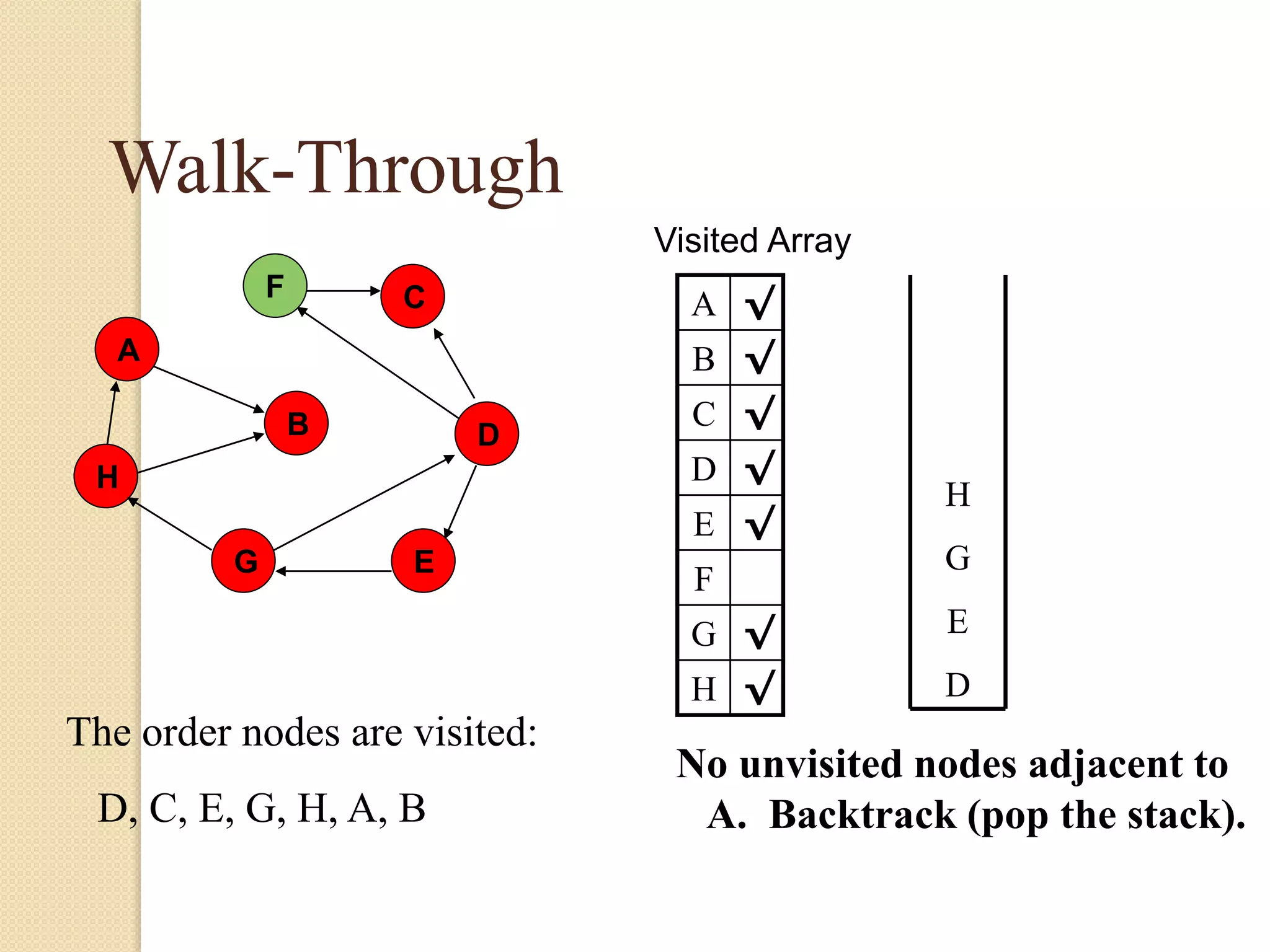
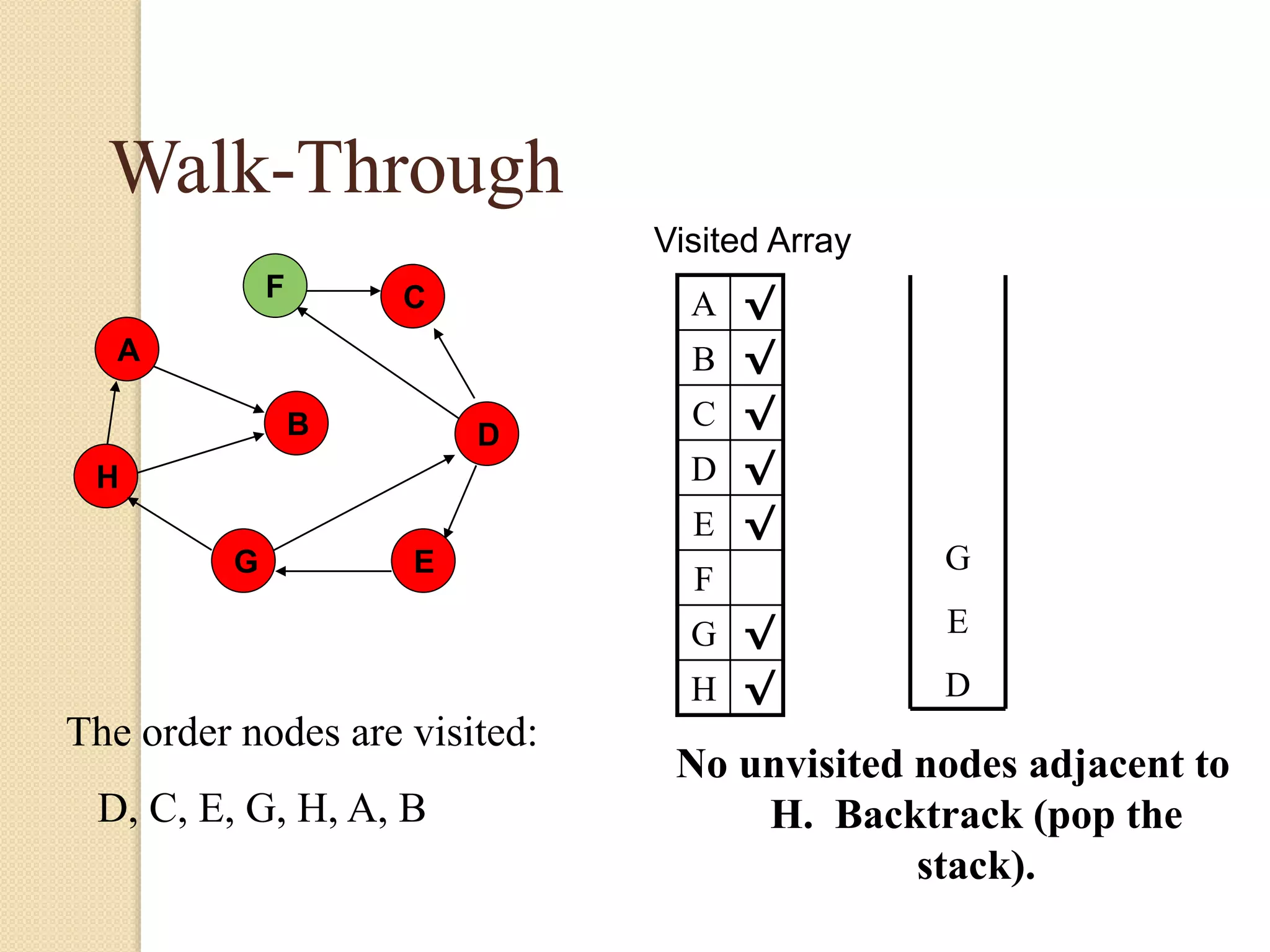
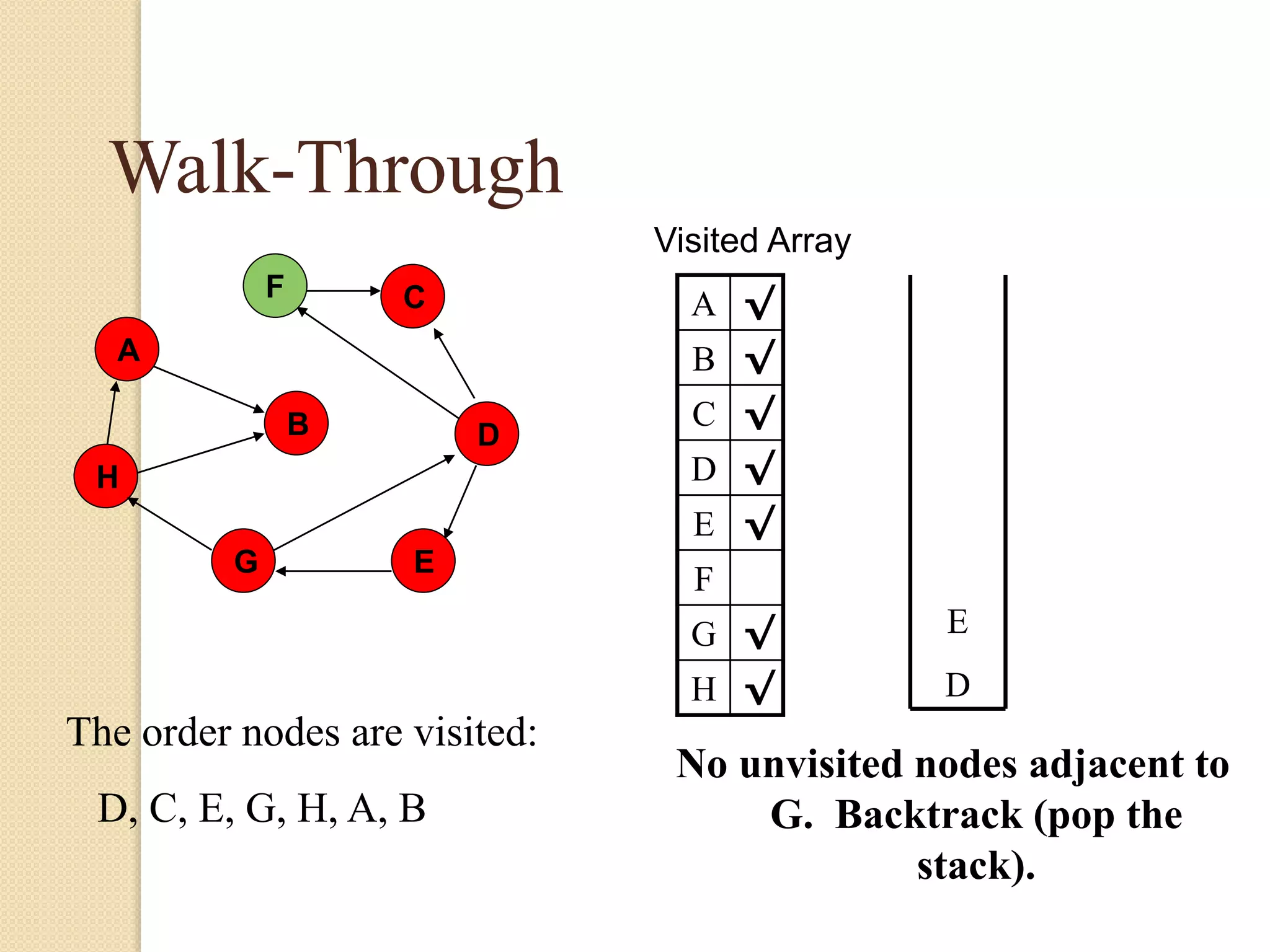
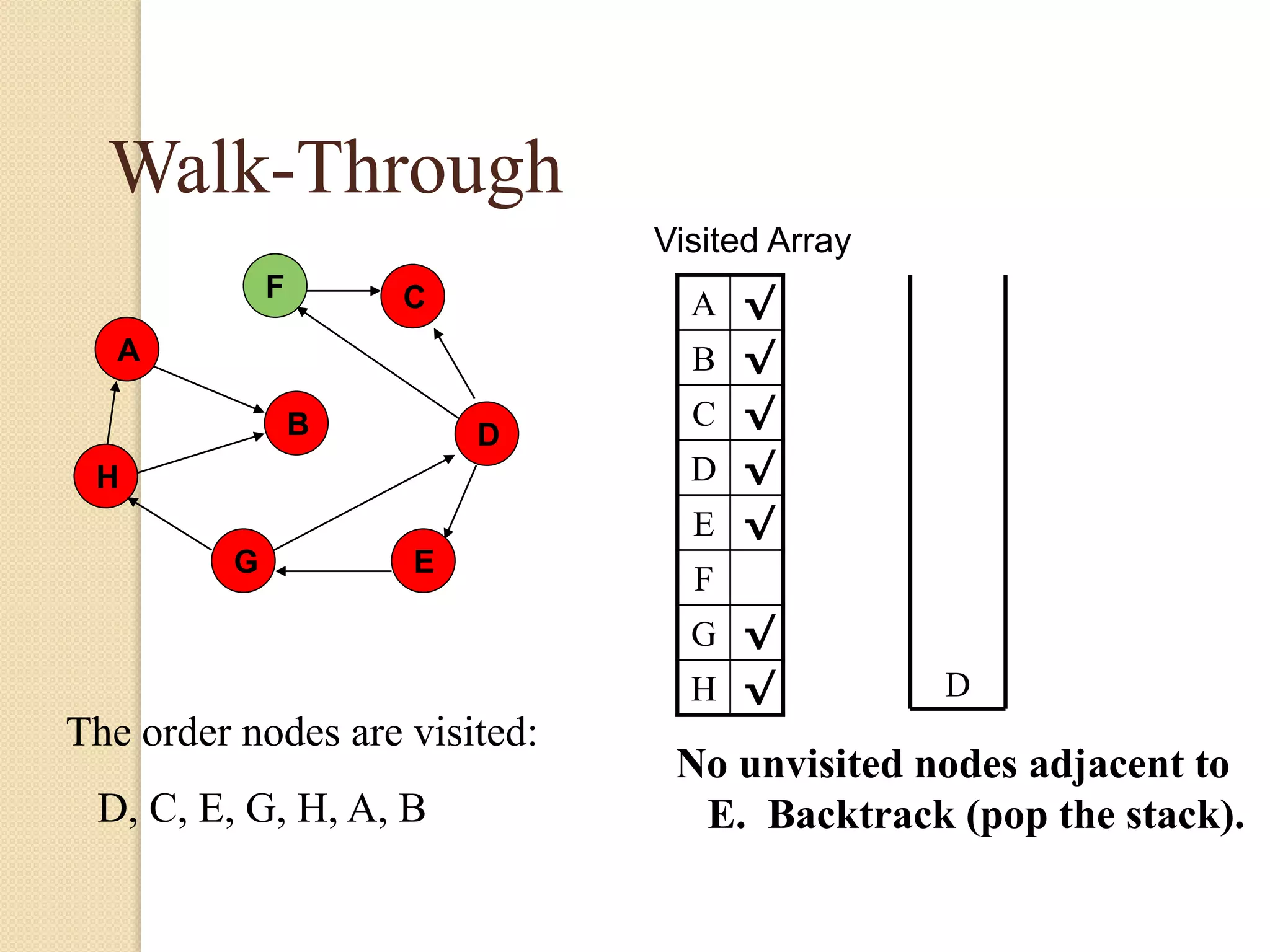
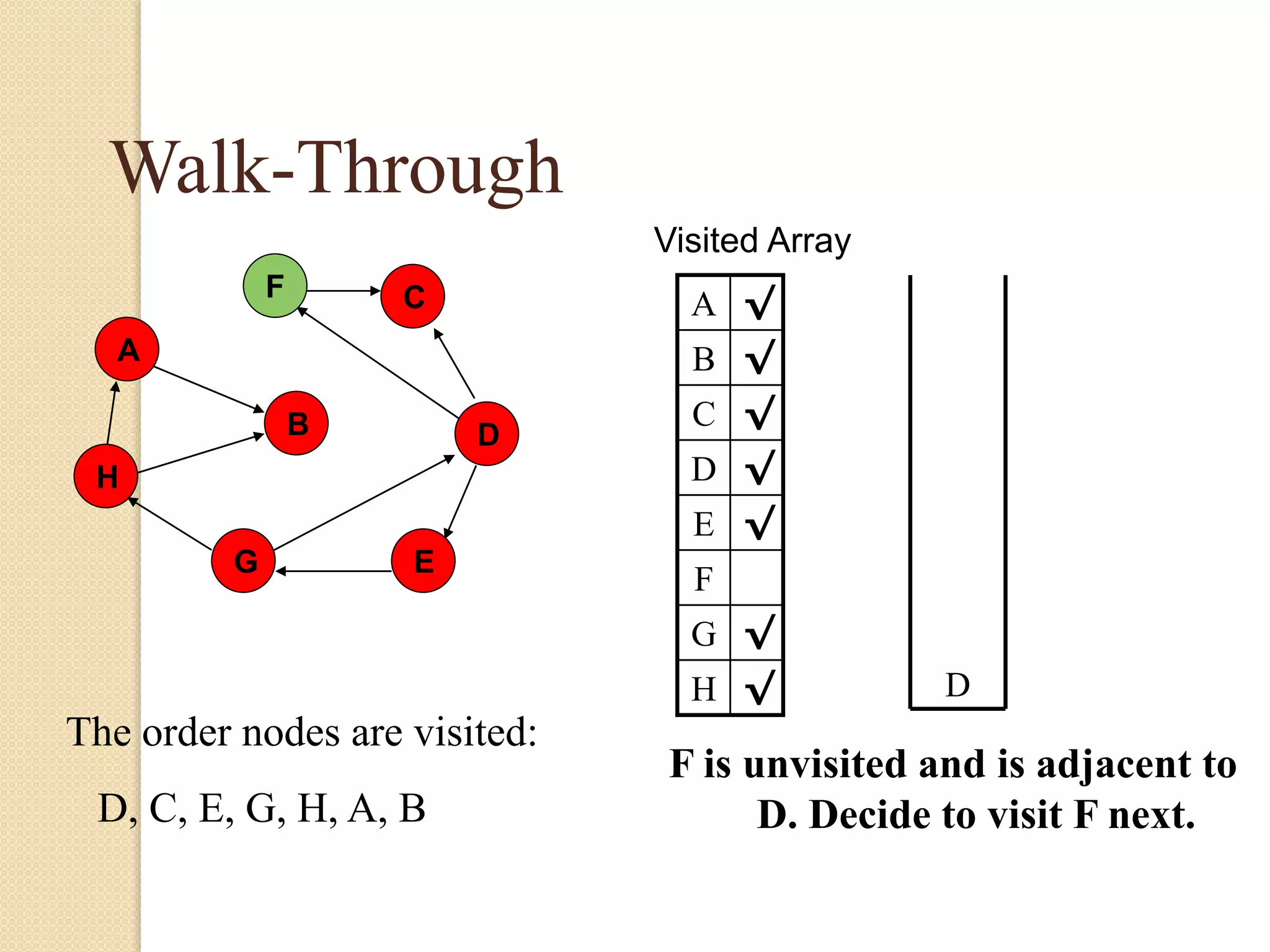
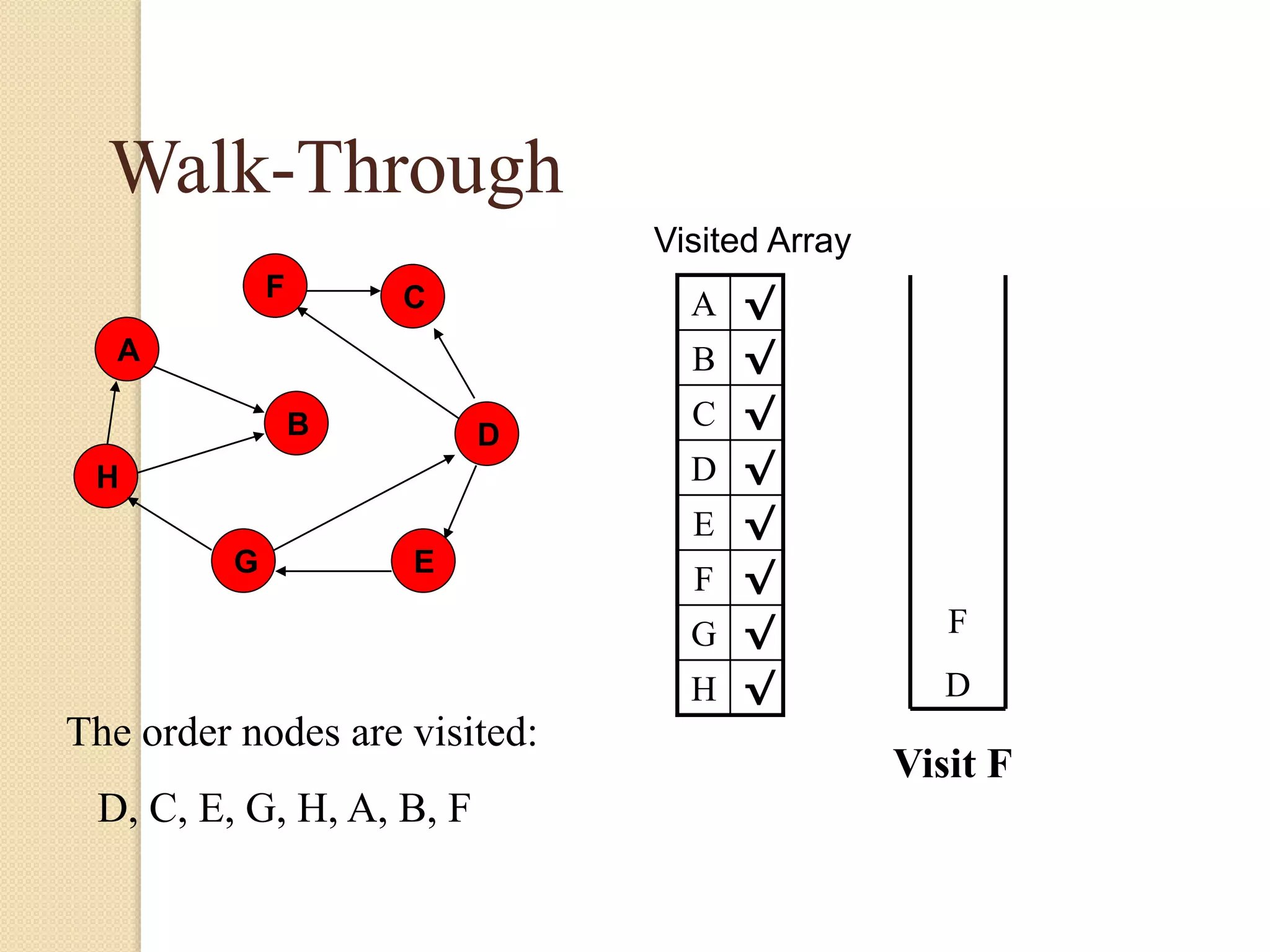
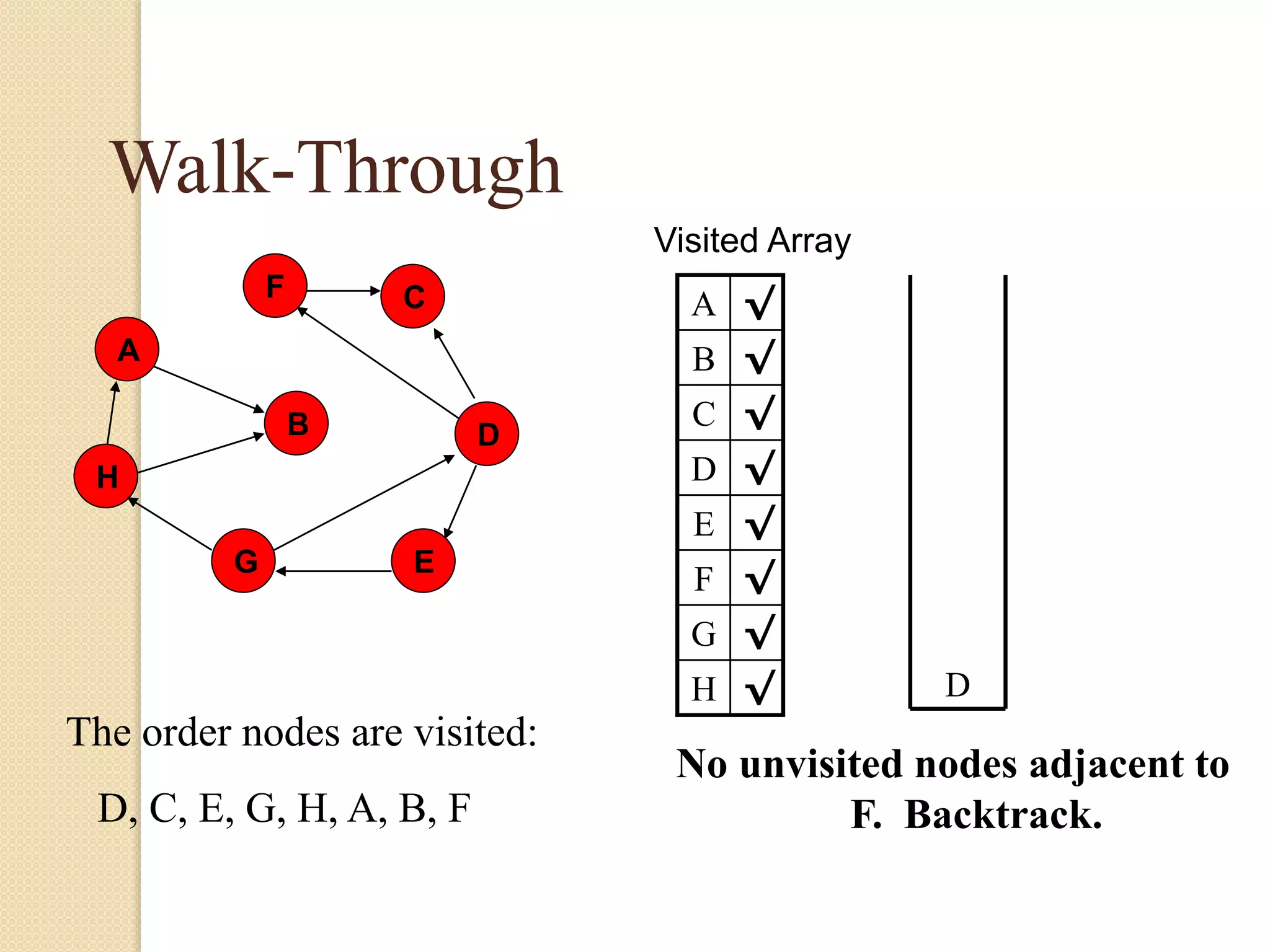
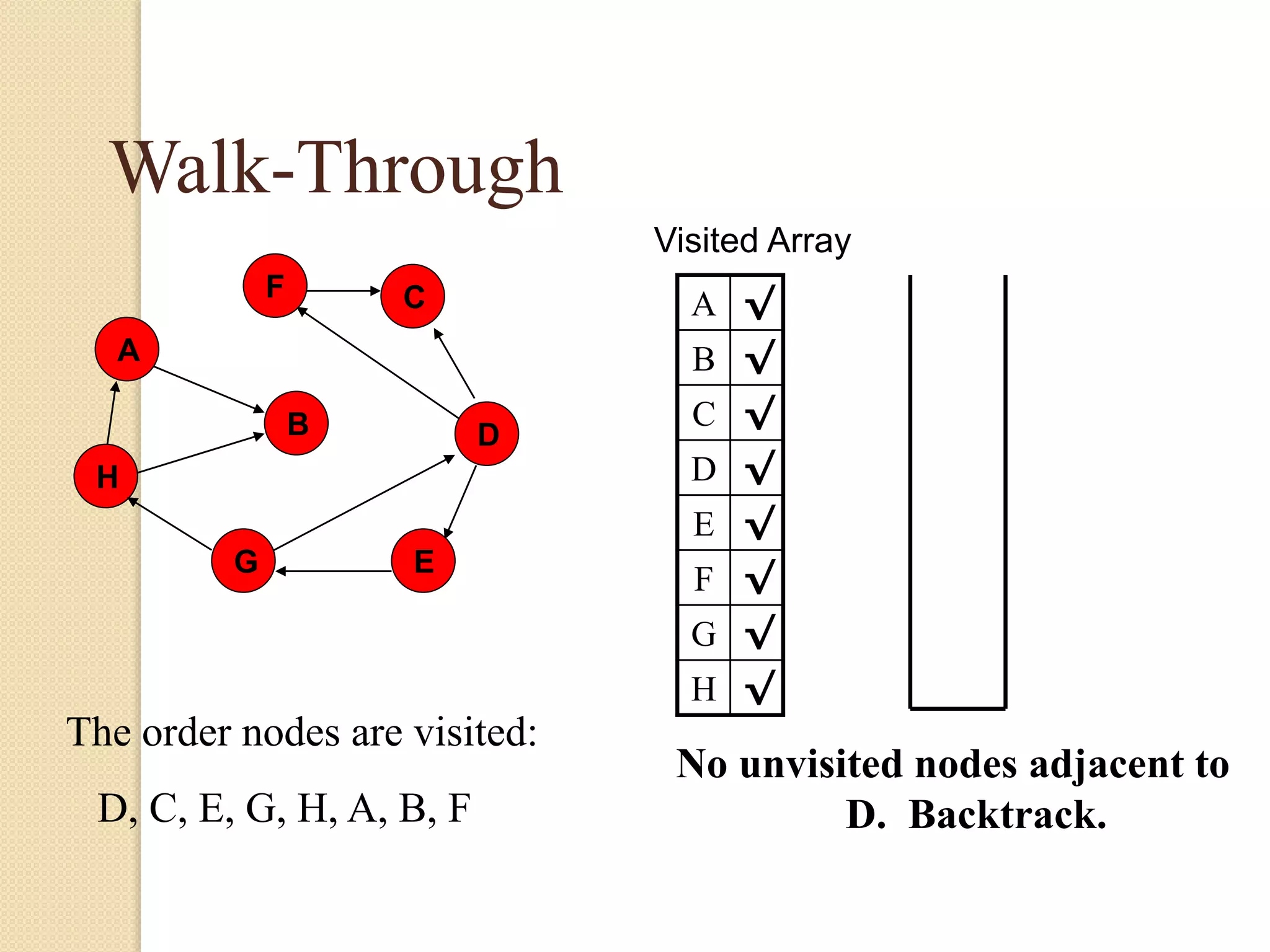
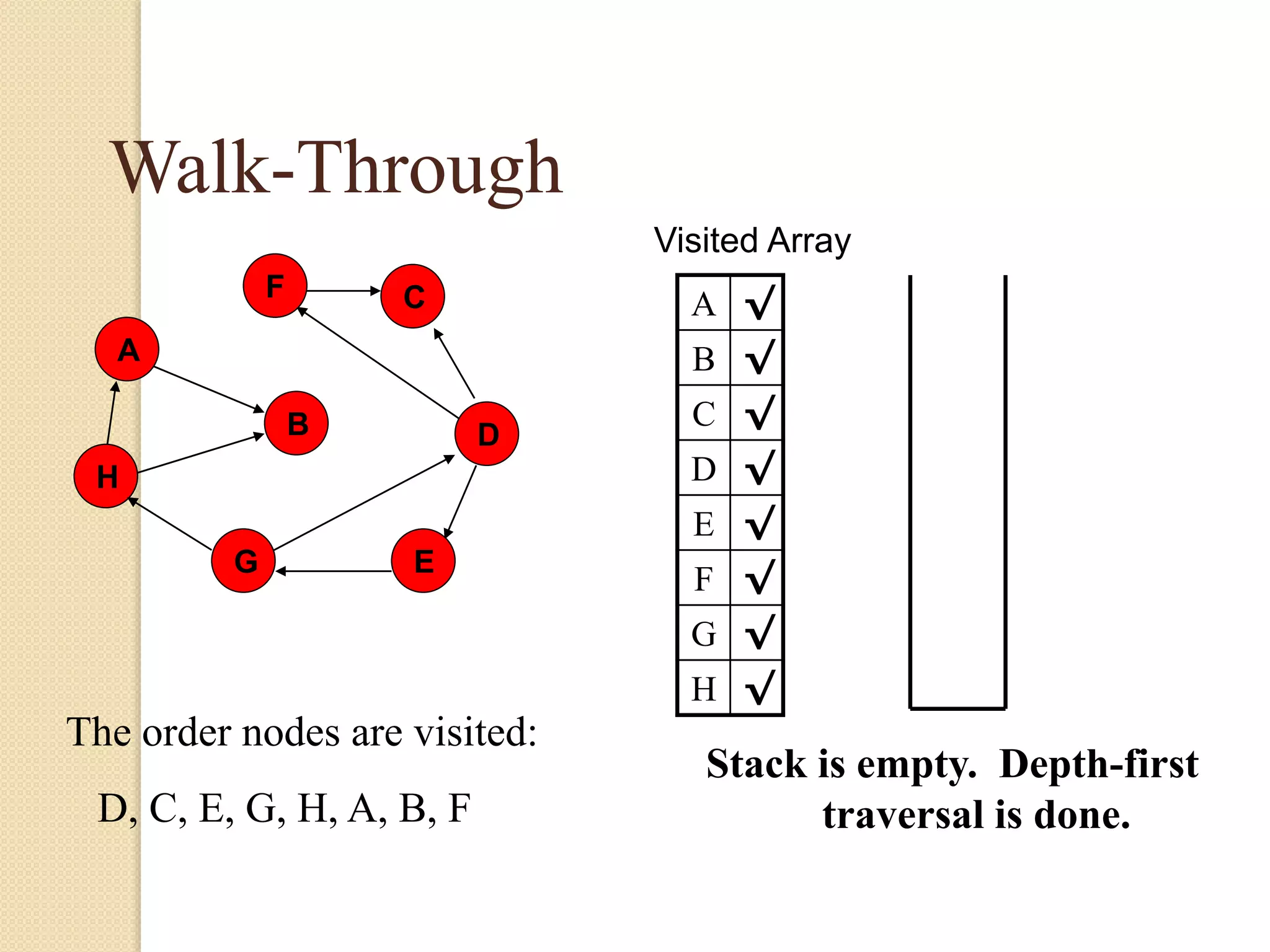
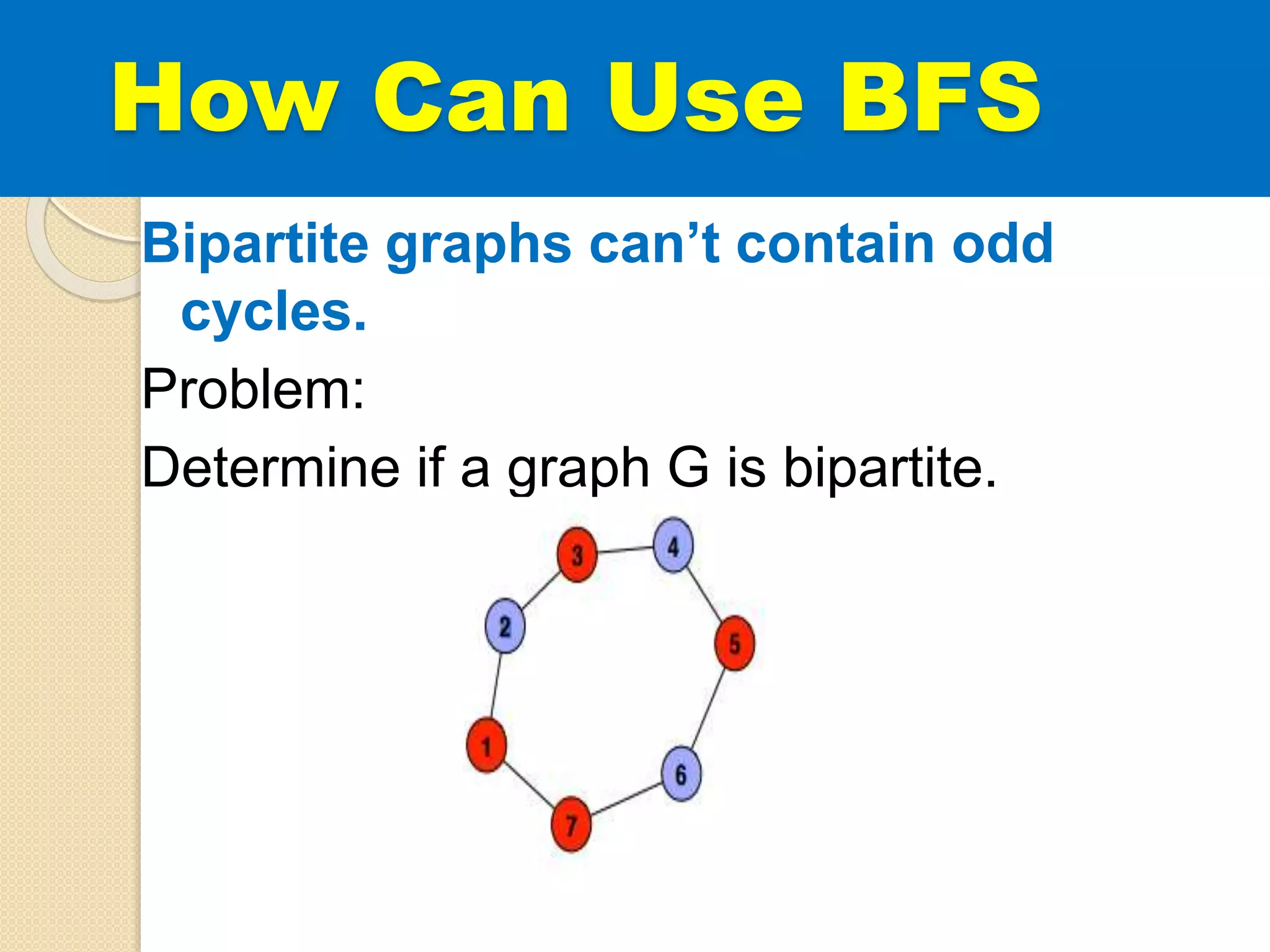
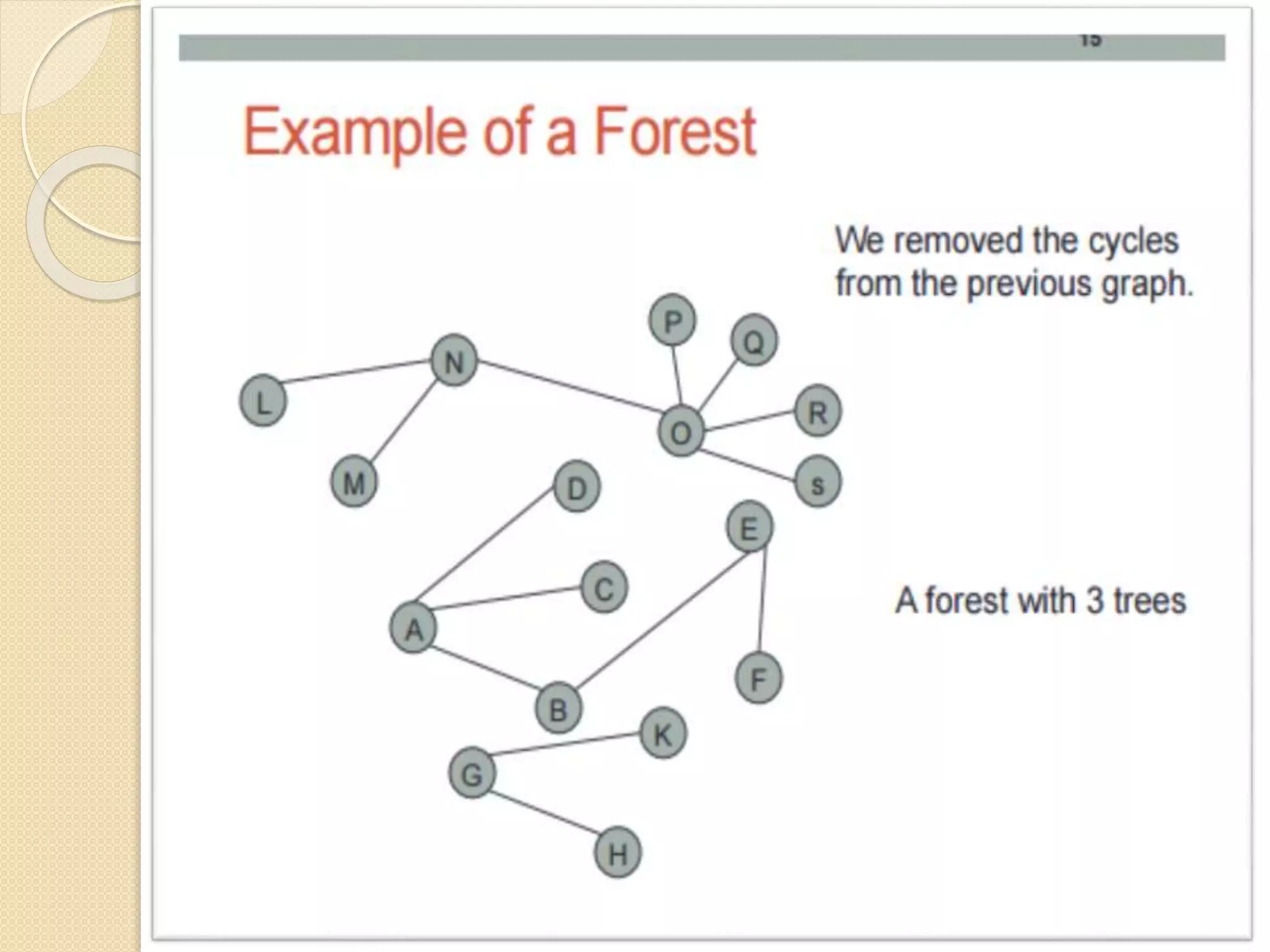
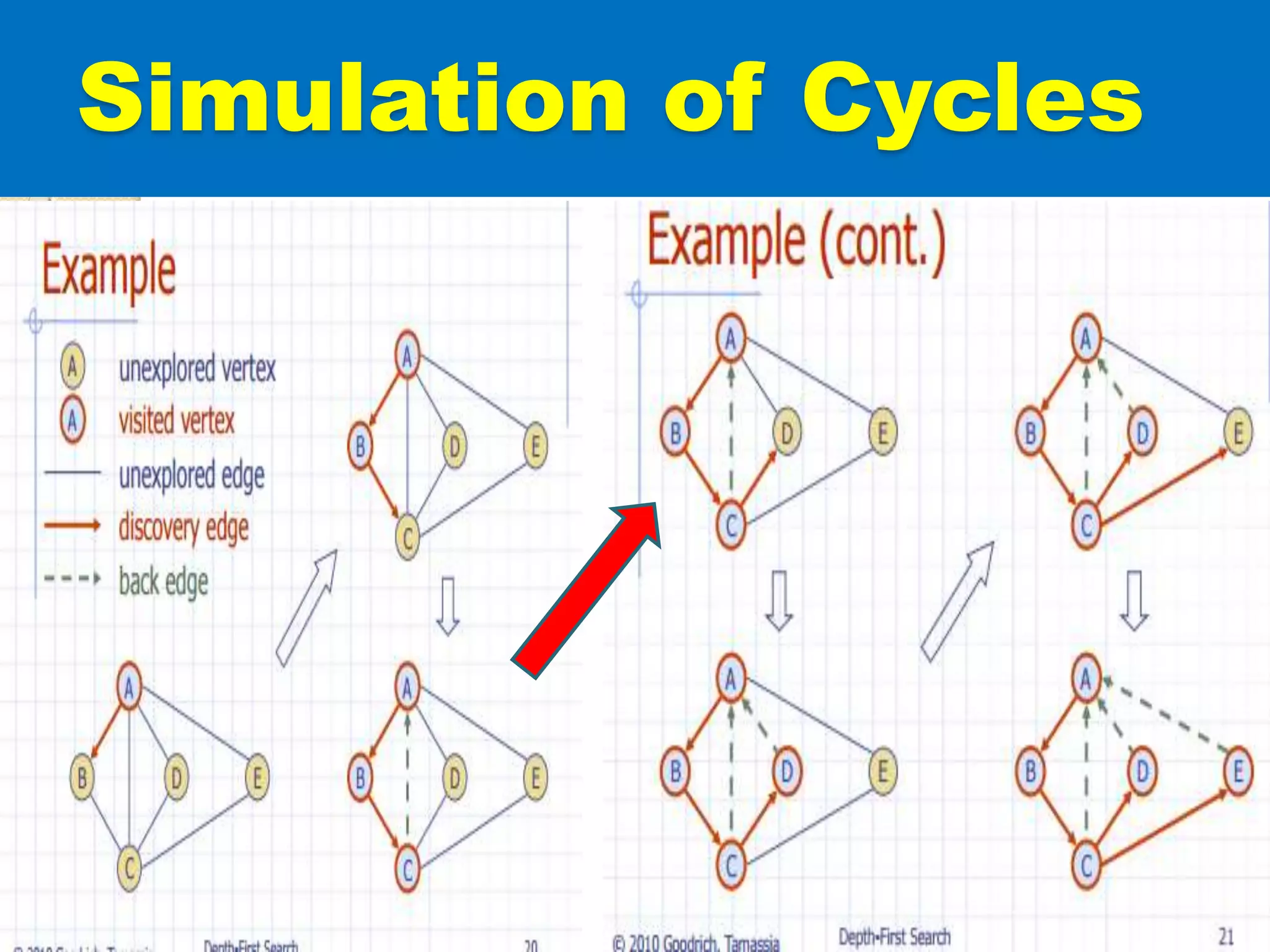
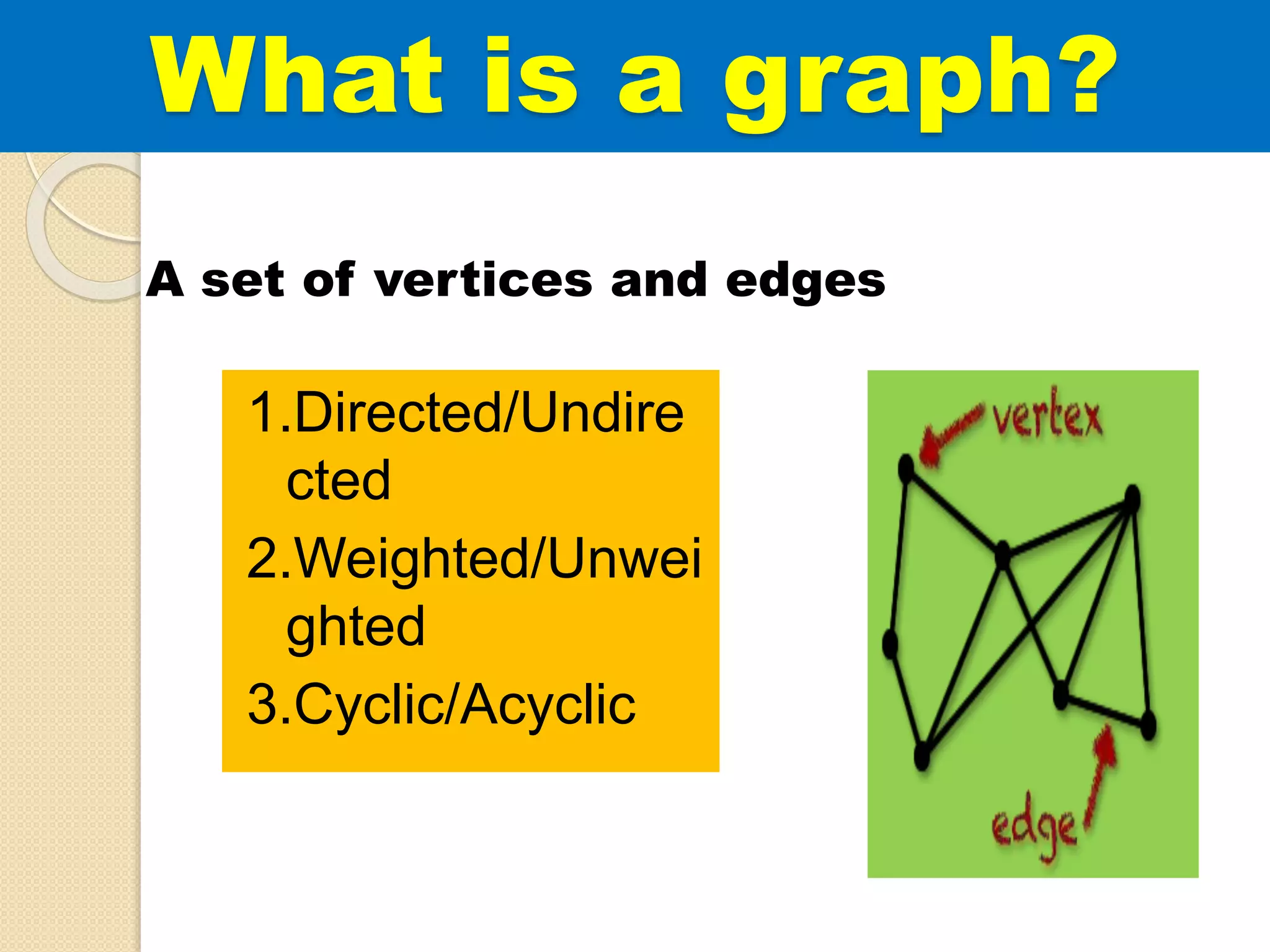
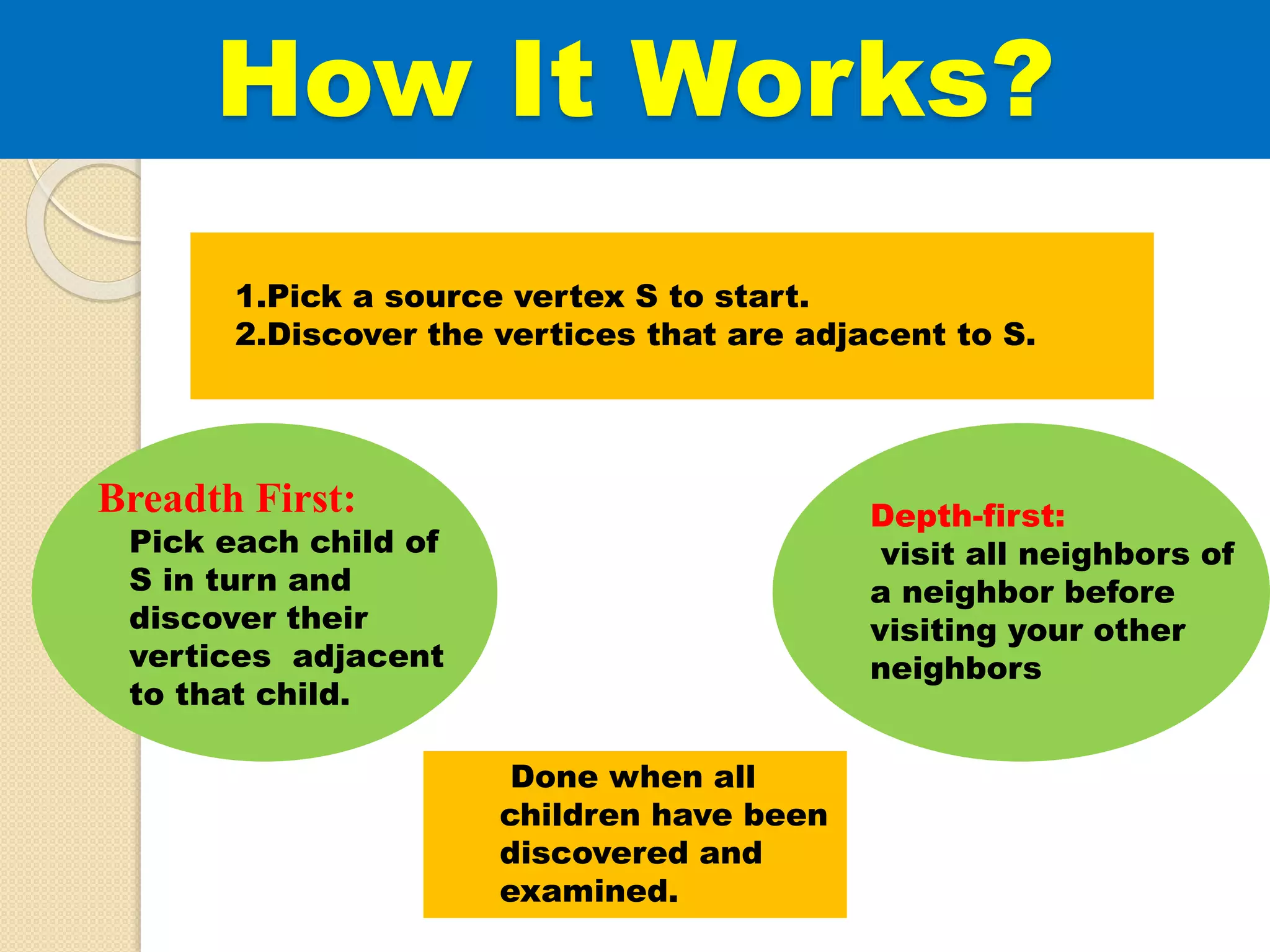
The document introduces breadth-first search (BFS) and depth-first search (DFS), two algorithms for traversing graphs. It provides explanations of how BFS and DFS work, including pseudocode algorithms. Examples of simulations of BFS and DFS on sample graphs are shown step-by-step with diagrams. Potential applications of BFS and DFS in areas like cycle detection, finding connected components, and topological sorting are also discussed.

1. WELCOME

2. Topic
BFS, DFS
And Their
Application

3. Contents
Introduction
Graph Traversal
How it works
Algorithm
Simulation of DFS & BFS
Analysis of BFS & DFS
Applications

4. Presented by
Anika Ohab
ID:142-15-3568
Abul Hasnath
ID:142-15-3532
Umme Habiba
ID: 142-15-3677
Shahinur Rahman
ID: 142-15-3606

5. What is a graph?
1.Directed/Undire
cted
2.Weighted/Unwei
ghted
3.Cyclic/Acyclic
A set of vertices and edges

6.  Breadth First Search (BFS)
Start several paths at a time, and advance in each one step at a time
The breadth-first search uses a FIFO queue.
 Depth First Search (DFS)
Once a possible path is found, continue the search until the end of
the path
The Depth-first search uses a LIFO Stack.
Graph Traversal

7. How It Works?
1.Pick a source vertex S to start.
2.Discover the vertices that are adjacent to S.
Depth-first:
visit all neighbors of
a neighbor before
visiting your other
neighbors
Breadth First:
Pick each child of
S in turn and
discover their
vertices adjacent
to that child.
Done when all
children have been
discovered and
examined.

8. Algorithm
BFS(G, s)
for each vertex u V [G] - {s}
do color[u] ← WHITE
d[u] ← ∞
π[u] ← NIL
color[s] ← GRAY
d[s] ← 0
π[s] ← NIL
Q ← Ø
ENQUEUE(Q, s)
while Q ≠ Ø
do u ← DEQUEUE(Q)
for each v Adj[u]
do if color[v] = WHITE
then color[v] ← GRAY
d[v] ← d[u] + 1
π[v] ← u
ENQUEUE(Q, v)
color[u] ← BLACK
DFS(G)
for each vertex u V [G]
do color[u] ← WHITE
π[u] ← NIL
time ← 0
for each vertex u V [G]
do if color[u] = WHITE
then DFS-VISIT(u)
DFS-VISIT(u)
color[u] ← GRAY ▹White vertex u
has just been discovered.
time ← time +1
d[u] time
for each v Adj[u] ▹Explore edge(u,
v).
do if color[v] = WHITE
then π[v] ← u
DFS-VISIT(v)
color[u] BLACK ▹ Blacken u; it is
finished.
f [u] ▹ time ← time +1

9. Simulation
of BFS

10. 3
1
6
10
9
7
12
3
Unvisite
d
6
7
This is starting node

11. 3
1
6
10
9
7
12
3
Unvisite
d
6
7
Unvisite
d
10

12. 3
1
6
10
9
7
12
6
7
10
Unvisite
d
9

13. 3
1
6
10
9
7
12
7
10
9
Unvisite
d
12

14. 3
1
6
10
9
7
12
10
9
12
visite
d

15. 3
1
6
10
9
7
12
9
12
visite
d

16. 3
1
6
10
9
7
12
12

17. Analysis of BFS
 For a Graph G=(V, E) and n = |V| and
m=|E|
 When Adjacency List is used
Complexity is O(m + n)
 When Adjacency Matrix is used
Scanning each row for checking the
connectivity of a Vertex is in order
O(n).
So, Complexity is O(n2 )

18. Simulation
of DFS

19. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C
D
E
F
G
H
Task: Conduct a depth-first search of the
graph starting with node D

20. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C
D √
E
F
G
H
Visit D
D
The order nodes are visited:
D

21. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C
D √
E
F
G
H
Consider nodes adjacent to D,
decide to visit C first (Rule:
visit adjacent nodes in
alphabetical order)
D
The order nodes are visited:
D

22. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E
F
G
H
Visit C
C
D
The order nodes are visited:
D, C

23. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E
F
G
H
No nodes adjacent to C; cannot
continue  backtrack, i.e.,
pop stack and restore
previous state
C
D
The order nodes are visited:
D, C

24. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E
F
G
H
Back to D – C has been visited,
decide to visit E next
D
The order nodes are visited:
D, C

25. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E √
F
G
H
Back to D – C has been visited,
decide to visit E next
E
D
The order nodes are visited:
D, C, E

26. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E √
F
G
H
Only G is adjacent to E
E
D
The order nodes are visited:
D, C, E

27. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E √
F
G √
H
Visit G
G
E
D
The order nodes are visited:
D, C, E, G

28. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E √
F
G √
H
Nodes D and H are adjacent to
G. D has already been
visited. Decide to visit H.
G
E
D
The order nodes are visited:
D, C, E, G

29. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E √
F
G √
H √
Visit H
H
G
E
D
The order nodes are visited:
D, C, E, G, H

30. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A
B
C √
D √
E √
F
G √
H √
Nodes A and B are adjacent to F.
Decide to visit A next.
H
G
E
D
The order nodes are visited:
D, C, E, G, H

31. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B
C √
D √
E √
F
G √
H √
Visit A
A
H
G
E
D
The order nodes are visited:
D, C, E, G, H, A

32. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B
C √
D √
E √
F
G √
H √
Only Node B is adjacent to A.
Decide to visit B next.
A
H
G
E
D
The order nodes are visited:
D, C, E, G, H, A

33. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
Visit B
B
A
H
G
E
D
The order nodes are visited:
D, C, E, G, H, A, B

34. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
No unvisited nodes adjacent to
B. Backtrack (pop the stack).
A
H
G
E
D
The order nodes are visited:
D, C, E, G, H, A, B

35. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
No unvisited nodes adjacent to
A. Backtrack (pop the stack).
H
G
E
D
The order nodes are visited:
D, C, E, G, H, A, B

36. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
No unvisited nodes adjacent to
H. Backtrack (pop the
stack).
G
E
D
The order nodes are visited:
D, C, E, G, H, A, B

37. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
No unvisited nodes adjacent to
G. Backtrack (pop the
stack).
E
D
The order nodes are visited:
D, C, E, G, H, A, B

38. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
No unvisited nodes adjacent to
E. Backtrack (pop the stack).
D
The order nodes are visited:
D, C, E, G, H, A, B

39. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F
G √
H √
F is unvisited and is adjacent to
D. Decide to visit F next.
D
The order nodes are visited:
D, C, E, G, H, A, B

40. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F √
G √
H √
Visit F
F
D
The order nodes are visited:
D, C, E, G, H, A, B, F

41. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F √
G √
H √
No unvisited nodes adjacent to
F. Backtrack.
D
The order nodes are visited:
D, C, E, G, H, A, B, F

42. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F √
G √
H √
No unvisited nodes adjacent to
D. Backtrack.
The order nodes are visited:
D, C, E, G, H, A, B, F

43. A
H
B
F
E
D
C
G
Walk-Through
Visited Array
A √
B √
C √
D √
E √
F √
G √
H √
Stack is empty. Depth-first
traversal is done.
The order nodes are visited:
D, C, E, G, H, A, B, F

44. For a Graph G=(V, E) and n = |V| and m=|E|
When Adjacency List is used Complexity is O(m + n)
When Adjacency Matrix is used Scanning each row
for checking the connectivity of a Vertex is in order O(n).
So, Complexity is O(n2 )
DFS uses space O(|V|) in the worst case to store the
stack of vertices on the current search path as well as
the set of already-visited vertices.
Analysis of DFS

45. BFS:
*Testing a graph for bipartiteness
*To find the shortest path from a vertex s to a
vertex v in an unweighted graph
*To find the length of such a path
*To find out if a graph contains cycles
*To construct a BSF tree/forest from a graph
*Copying garbage collection
Applications

46. DFS:
* Finding connected components.
*Topological sorting.
*Finding the bridges of a graph.
*cycle Detecting
*Finding strongly connected components.
*Finding biconnectivity in graphs.
Applications

47. How Can Use BFS
Bipartite graphs can’t contain odd
cycles.
Problem:
Determine if a graph G is bipartite.

48. Testing Bipartiteness
How can we test if G is bipartite?
1.Do a BFS starting from some node s.
2.Color even levels “blue” and odd levels
“red.”
3.Check each edge to see if any edge has
both endpoints the same color.

49. COMPUTING SPANNING
FORESTS
In graphs that are not connected, there can be no
spanning tree, and one must consider spanning
forests instead.

51. Finding Cycles Using DFS
• Similar to using BFS.
• For undirected graphs, classify the edges
into 3 categories during program
execution:
1.unvisited edge
2.discovery edge and
3.back (cross) edge.
• If there exists a back edge, the
undirected graph contains a cycle.

52. Simulation of Cycles