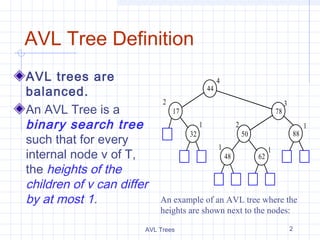
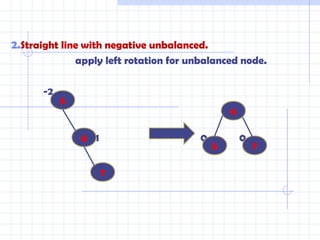
An AVL tree is a self-balancing binary search tree where the heights of the two child subtrees of every node differ by at most one. This balances the tree during insertion and deletion operations and ensures searching, insertion, and deletion all take O(log n) time. The tree undergoes single or double rotations to maintain balance after insertions or deletions by making the node with the largest subtree height become the new root of a local subtree.

1. AVL Trees
6
v
3 8
z
4
AVL Trees 1

2. AVL Tree Definition
AVL trees are 4
balanced. 44
2
An AVL Tree is a
3
17 78
binary search tree 1 2 1
such that for every
32 50 88
1
internal node v of T, 48 62
1
the heights of the
children of v can differ
by at most 1. An example of an AVL tree where the
heights are shown next to the nodes:
AVL Trees 2

3.
AVL Trees:
AVL trees were invented in 1962 by two Russian
scientist G.M Adelson Velsky & E.M Landis.
Definition:
An AVL tree is a binary search tree in which the balance
factor of every node, which is defined as the difference b/w the
heights of the node’s left & right sub trees is either 0 or +1
or -1 .
Balance factor = ht of left sub tree – ht of right sub tree.
ht=height

4. Example :
AVL tree BST ( not AVL tree )
1 2
10 10
0 5 1 20 05 020
1 4 -1 0 1 -1
7 4 7
12
0 0 0 0
2 8
2
8

5.
If an insertion of a new node makes an AVL tree
unbalanced , we transform the tree by a rotation
Rotation :
A Rotation in an AVL tree is a local transformation of
its sub tree rooted at a node whose balance has become either
+2 or -2 ,if there are several such nodes, we rotate the tree
rooted at the unbalanced node that is the closest to the newly
inserted leaf.

6.
Types of rotations :
Totally there are four types of rotations
1. Single right rotation or R-rotation
2. Single left rotation or L-rotation
3. Double right-left rotation or RL-rotation
4. Double left-right rotation or LR-rotation

7.
Points to remember to select different rotation technique :
1.Straight line with positive unbalanced.
apply Right rotation for unbalanced node.
+2
5 04
+1 4 0 0
2 5
0
2

8.
2.Straight line with negative unbalanced.
apply left rotation for unbalanced node.
-2
5
06
6 -1 0 0
5 7
70

9.
3.Curved line with positive unbalanced.
apply left-right rotation.
Right rotation for unbalanced node and left rotation
for the nearest node.
+2
5 0
4
4 -1
0 2 5 0
2 0

10.
4.Curved line with negative unbalanced.
apply right-left rotation.
Left rotation for unbalanced node and right rotation
for the nearest node.
-2
5 0
7
+1 8
0 5 8 0
0 7

11. n(2) 3
n(1)
Height of an AVL Tree
4
Fact: The height of an AVL tree storing n keys is O(log
n).
Proof: Let us bound n(h): the minimum number of internal
nodes of an AVL tree of height h.
We easily see that n(1) = 1 and n(2) = 2
For n > 2, an AVL tree of height h contains the root node,
one AVL subtree of height n-1 and another of height n-2.
That is, n(h) = 1 + n(h-1) + n(h-2)
Knowing n(h-1) > n(h-2), we get n(h) > 2n(h-2). So
n(h) > 2n(h-2), n(h) > 4n(h-4), n(h) > 8n(n-6), … (by induction),
n(h) > 2in(h-2i)
Solving the base case we get: n(h) > 2 h/2-1
Taking logarithms: h < 2log n(h) +2
Thus the height of an AVL Trees is O(log n)
AVL tree 11

12. Insertion in an AVL Tree
Insertion is as in a binary search tree
Always done by expanding an external node.
Example: 44 44
c=z
17 78 17 78
a=y
32 50 88 32 50 88
48 62 48 62
b=x
54
w
before insertion after insertion
AVL Trees 12

13. Trinode Restructuring
let (a,b,c) be an inorder listing of x, y, z
perform the rotations needed to make b the topmost node of the
three
(other two cases
a=z case 2: double rotation
a=z are symmetrical)
(a right rotation about c,
c=y then a left rotation about a)
b=y
T0
T0
c=x b=x
T3
T1 b=y b=x
T1 T2
T2 T3
a=z c=x a=z c=y
case 1: single rotation
(a left rotation about a) T0 T1 T2 T3 T0 T1 T2 T3
AVL Trees 13

14. Insertion Example, continued
5
44
2
z 64
17 78 7
3
2y 1
1
32 1 50 4 88
1
2 x
48
1
3 62
5
54 T3
unbalanced... T2
T0
4
T1 44 4
2 3 x
17
2 y 62
z6
1 2 2
32
1
1 50 3 5
78 7
1 1
...balanced 48 54 88
T2
T0 T1 T3
AVL Trees 14

15. Restructuring
(as Single Rotations)
Single Rotations:
a=z single rotation b=y
b=y a=z c=x
c=x
T0 T3
T1 T3 T0 T1 T2
T2
c=z single rotation b=y
b=y a=x c=z
a=x
T3 T3
T0 T2 T2 T1 T0
T1
AVL Trees 15

16. Restructuring
(as Double Rotations)
double rotations:
a=z double rotation b=x
c=y a=z c=y
b=x
T0 T2
T2 T3 T0 T1 T3
T1
c=z double rotation b=x
a=y a=y c=z
b=x
T0 T2
T3 T2 T3 T1 T0
T1
AVL Trees 16

17. Removal in an AVL Tree
Removal begins as in a binary search tree, which
means the node removed will become an empty
external node. Its parent, w, may cause an imbalance.
Example: 44 44
17 62 17 62
32 50 78 50 78
48 54 88 48 54 88
before deletion of 32 after deletion
AVL Trees 17

18. Rebalancing after a Removal
Let z be the first unbalanced node encountered while travelling
up the tree from w. Also, let y be the child of z with the larger
height, and let x be the child of y with the larger height.
We perform restructure(x) to restore balance at z.
As this restructuring may upset the balance of another node
higher in the tree, we must continue checking for balance until
the root of T is reached
62
a=z 44
44 78
w 17 62 b=y
17 50 88
50 78 c=x
48 54
48 54 88
AVL Trees 18

19. Running Times for
AVL Trees
a single restructure is O(1)
 using a linked-structure binary tree
find is O(log n)
 height of tree is O(log n), no restructures needed
insert is O(log n)
 initial find is O(log n)
 Restructuring up the tree, maintaining heights is O(log n)
remove is O(log n)
 initial find is O(log n)
 Restructuring up the tree, maintaining heights is O(log n)
AVL Trees 19