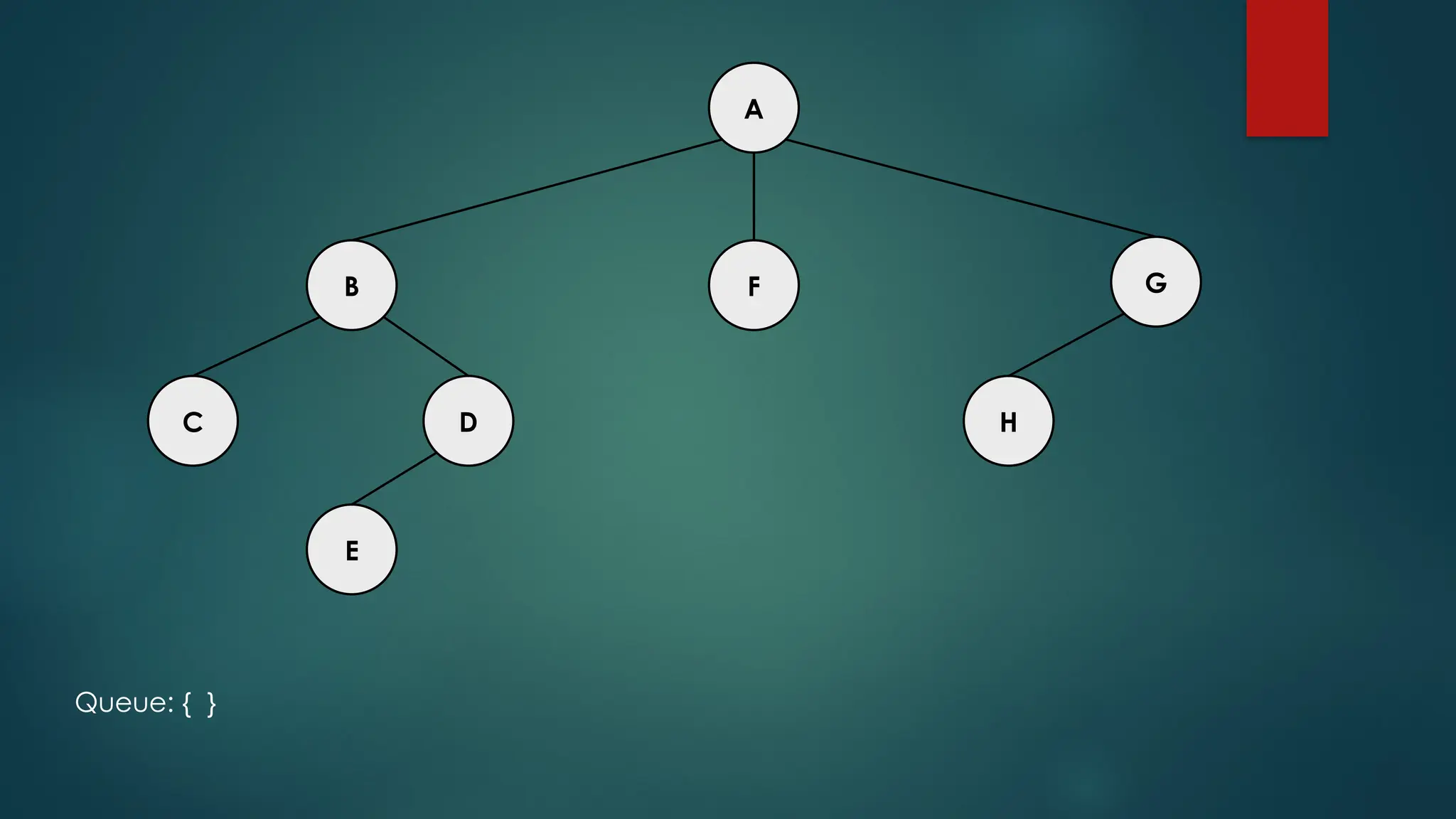
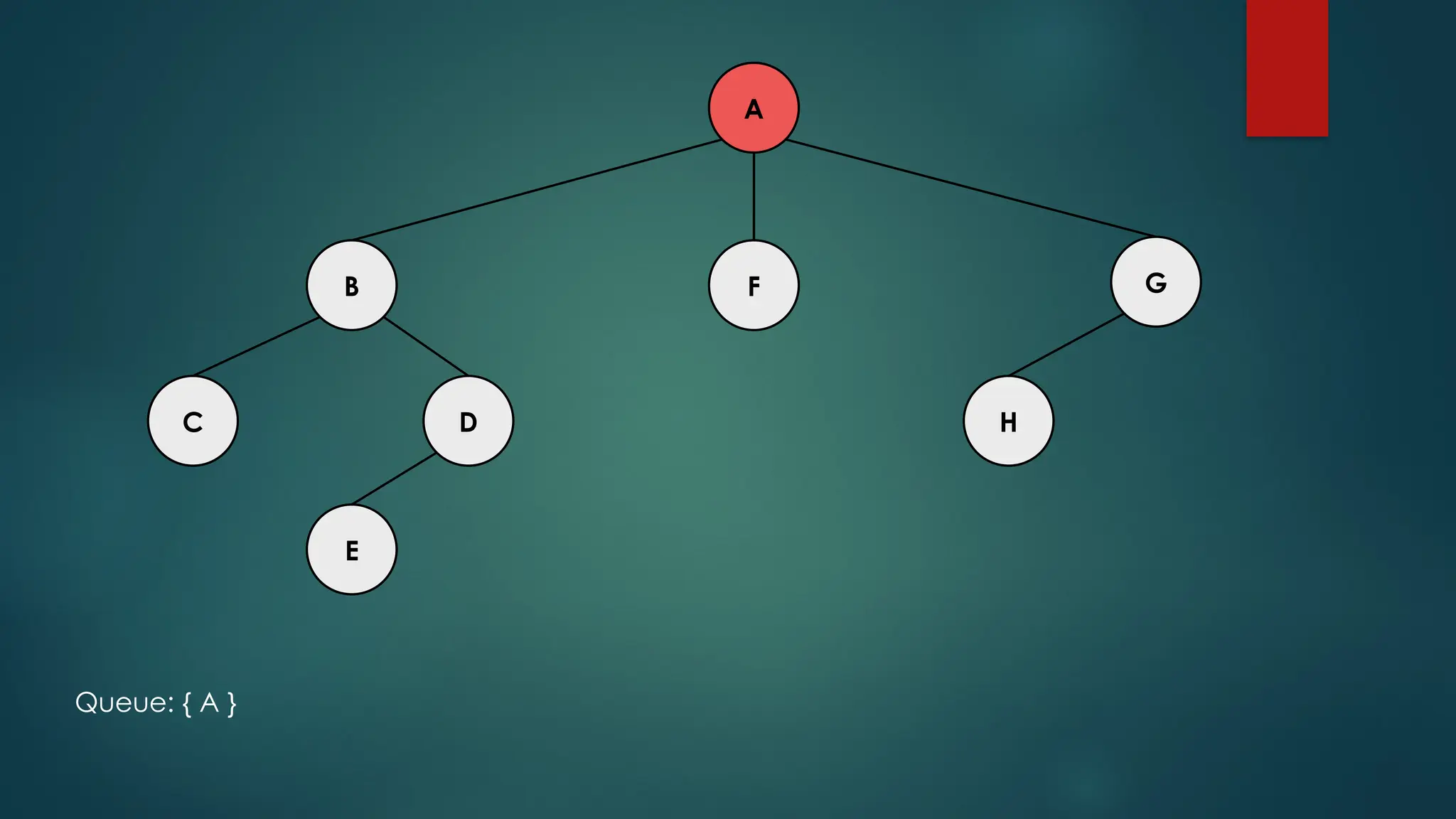
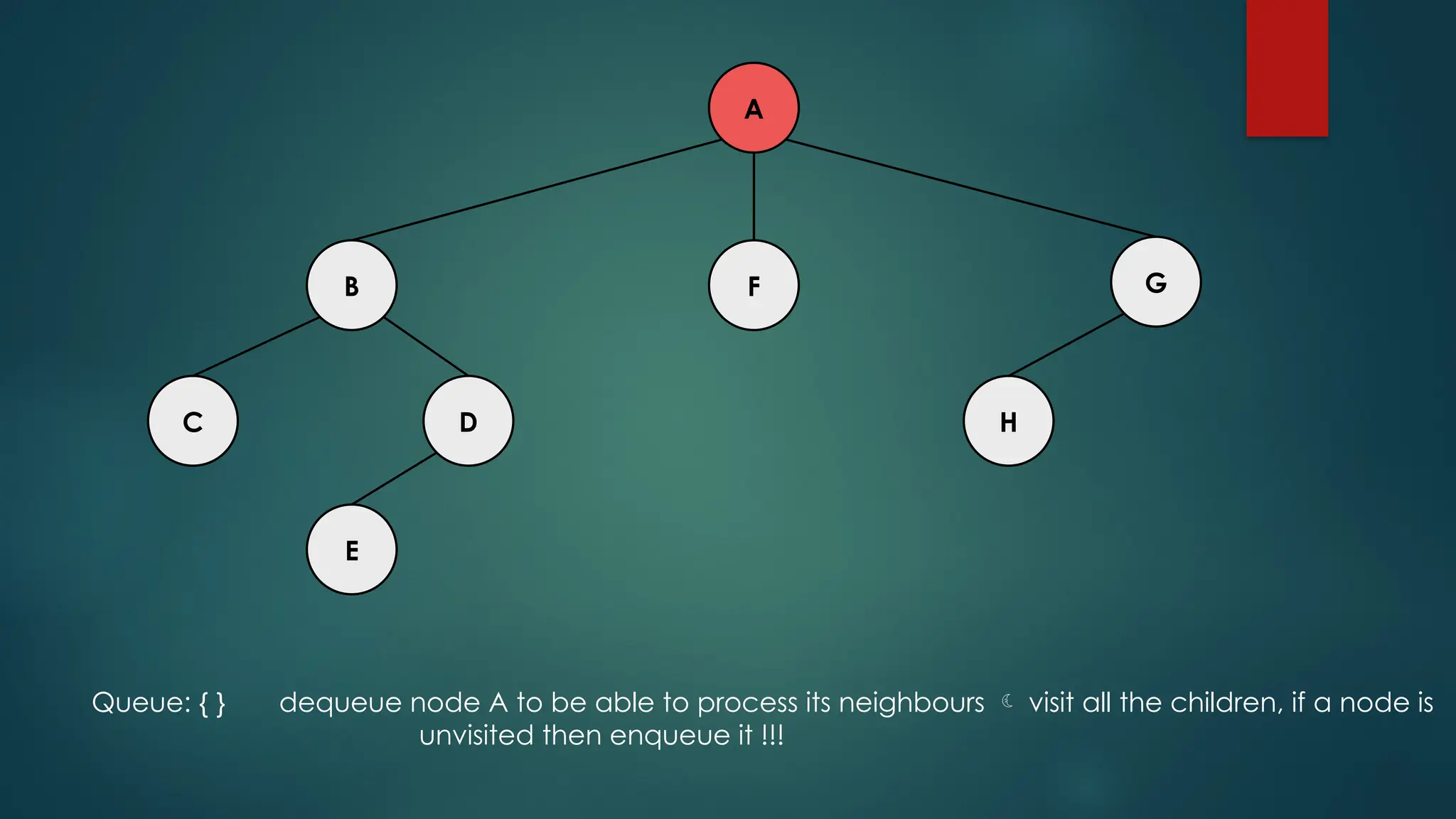
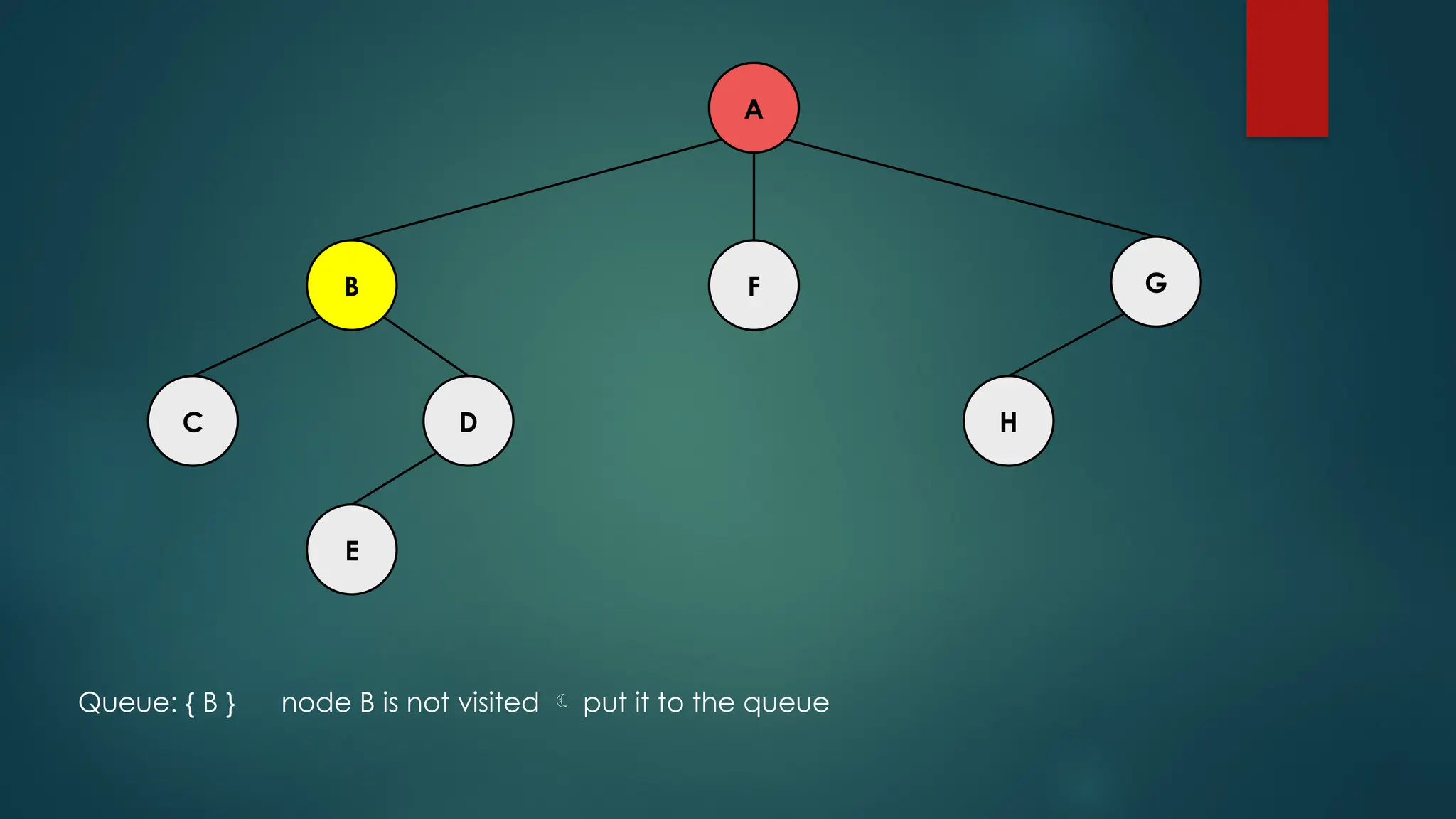
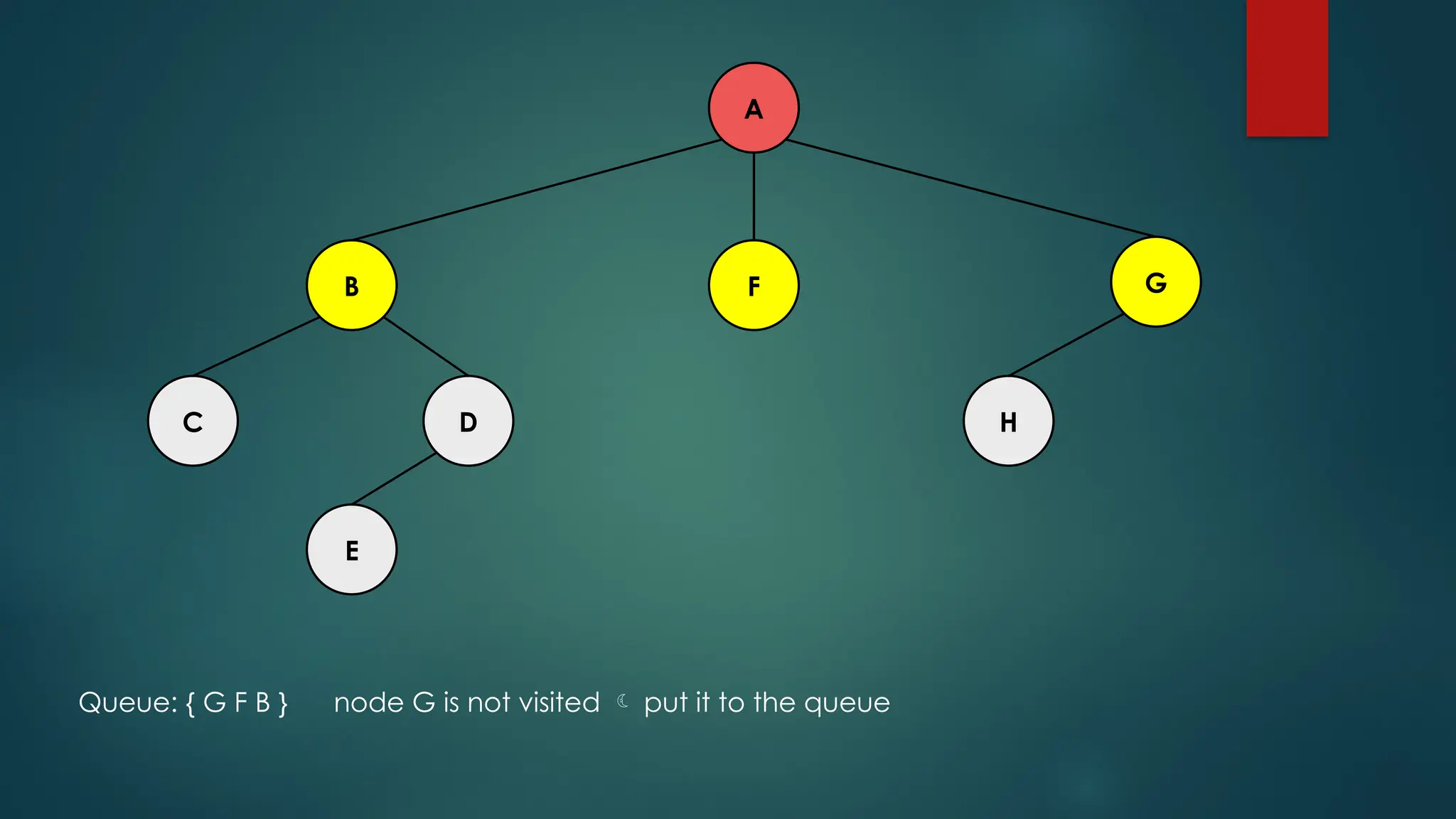
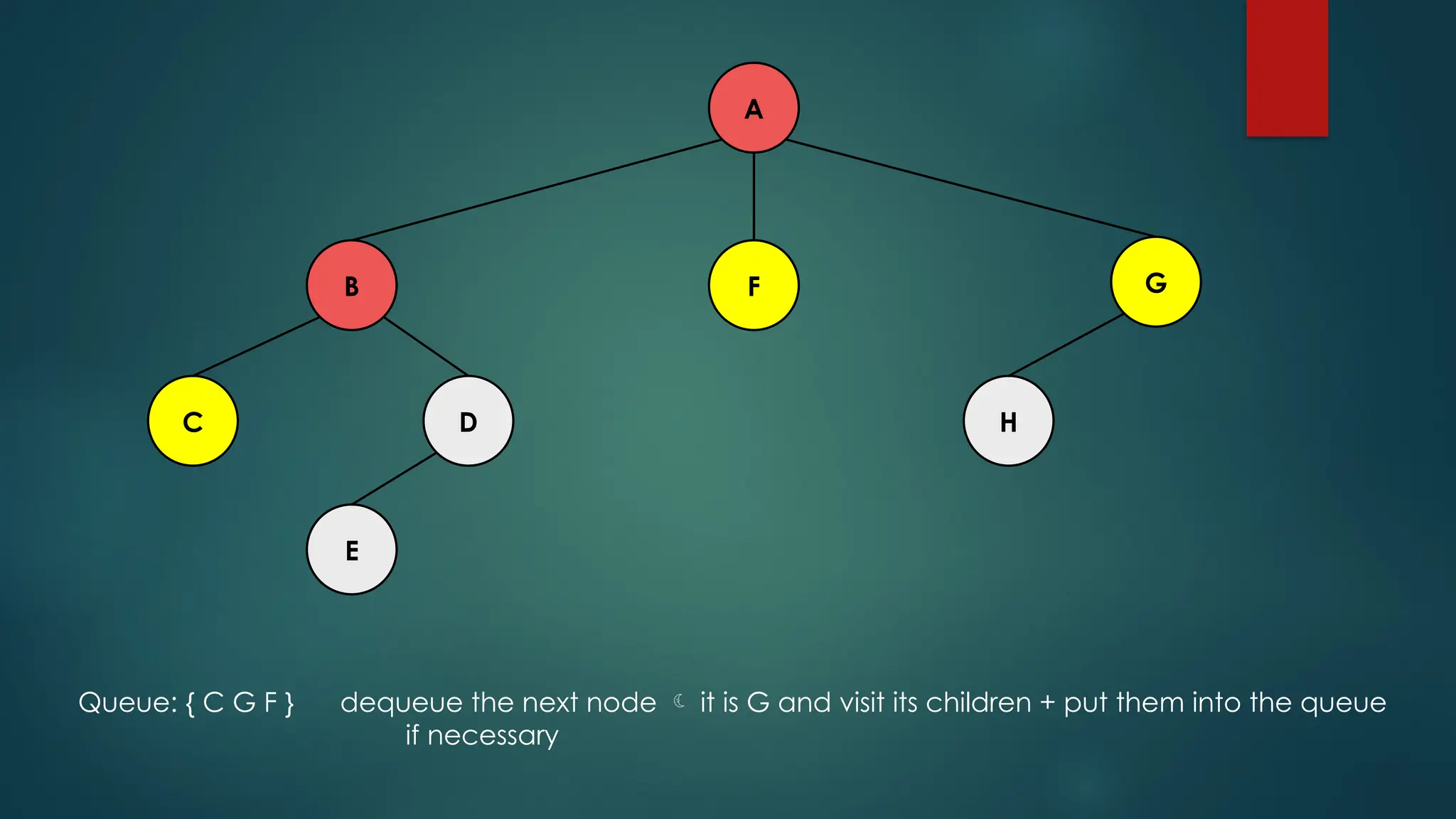
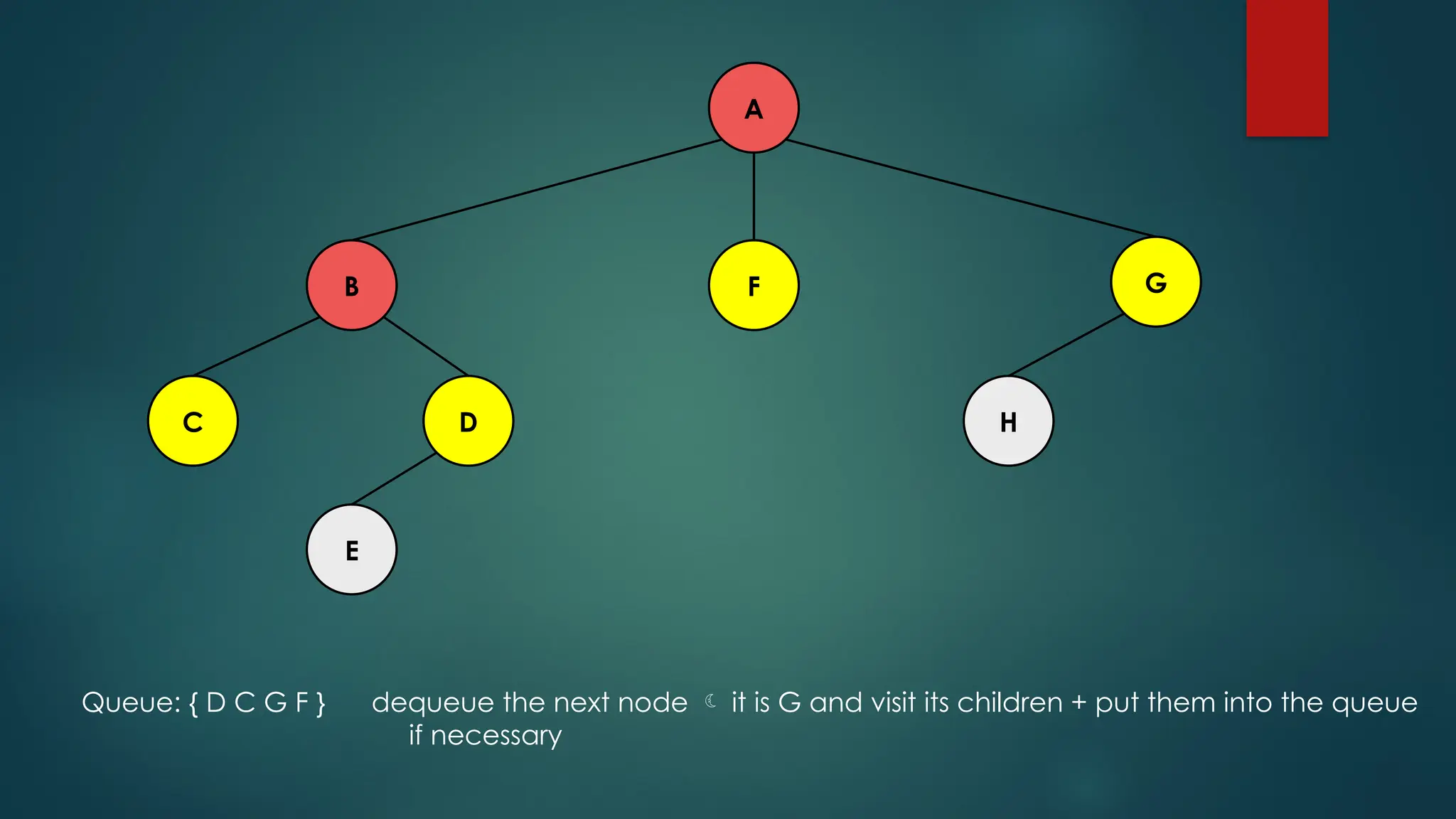
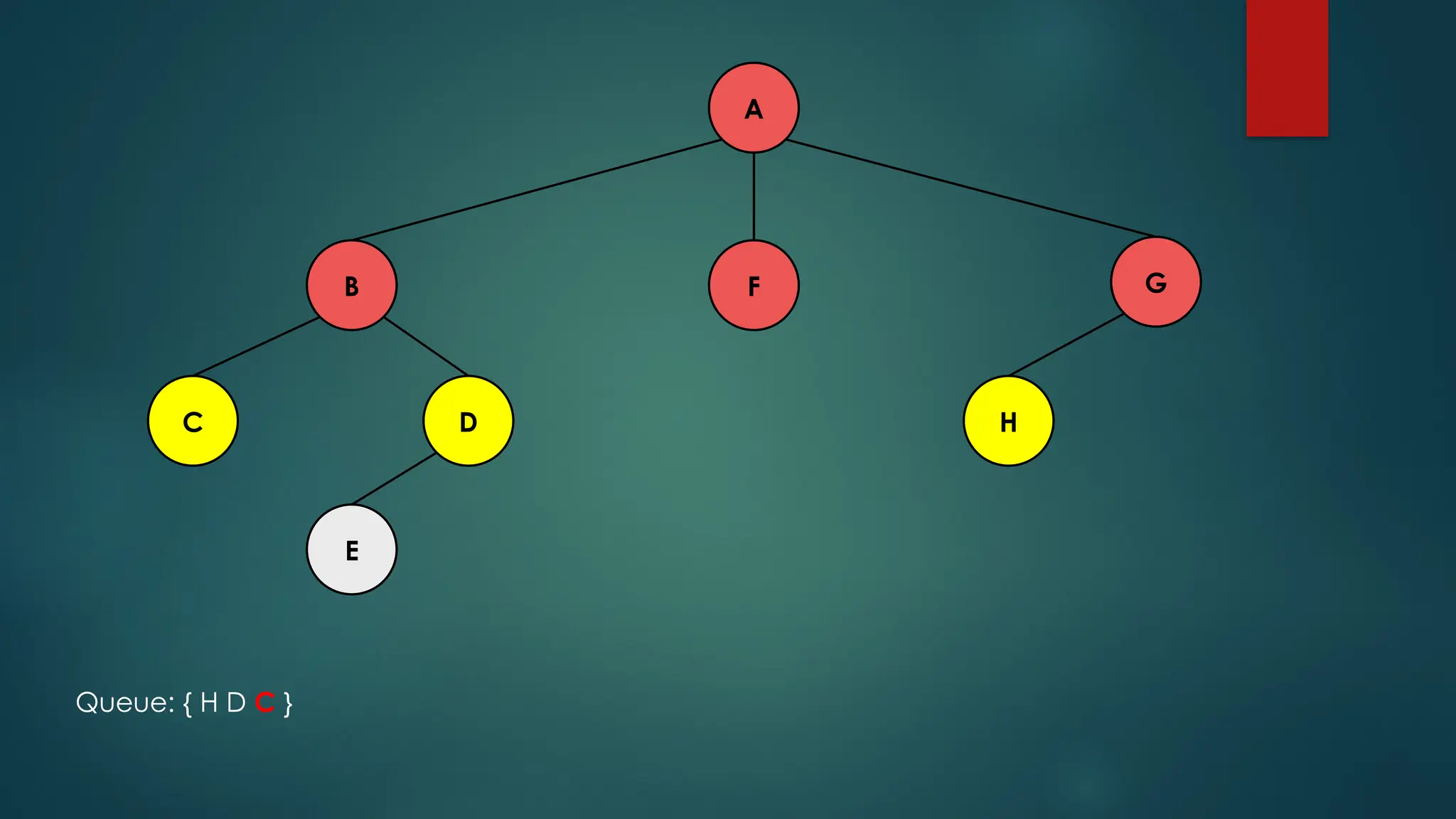
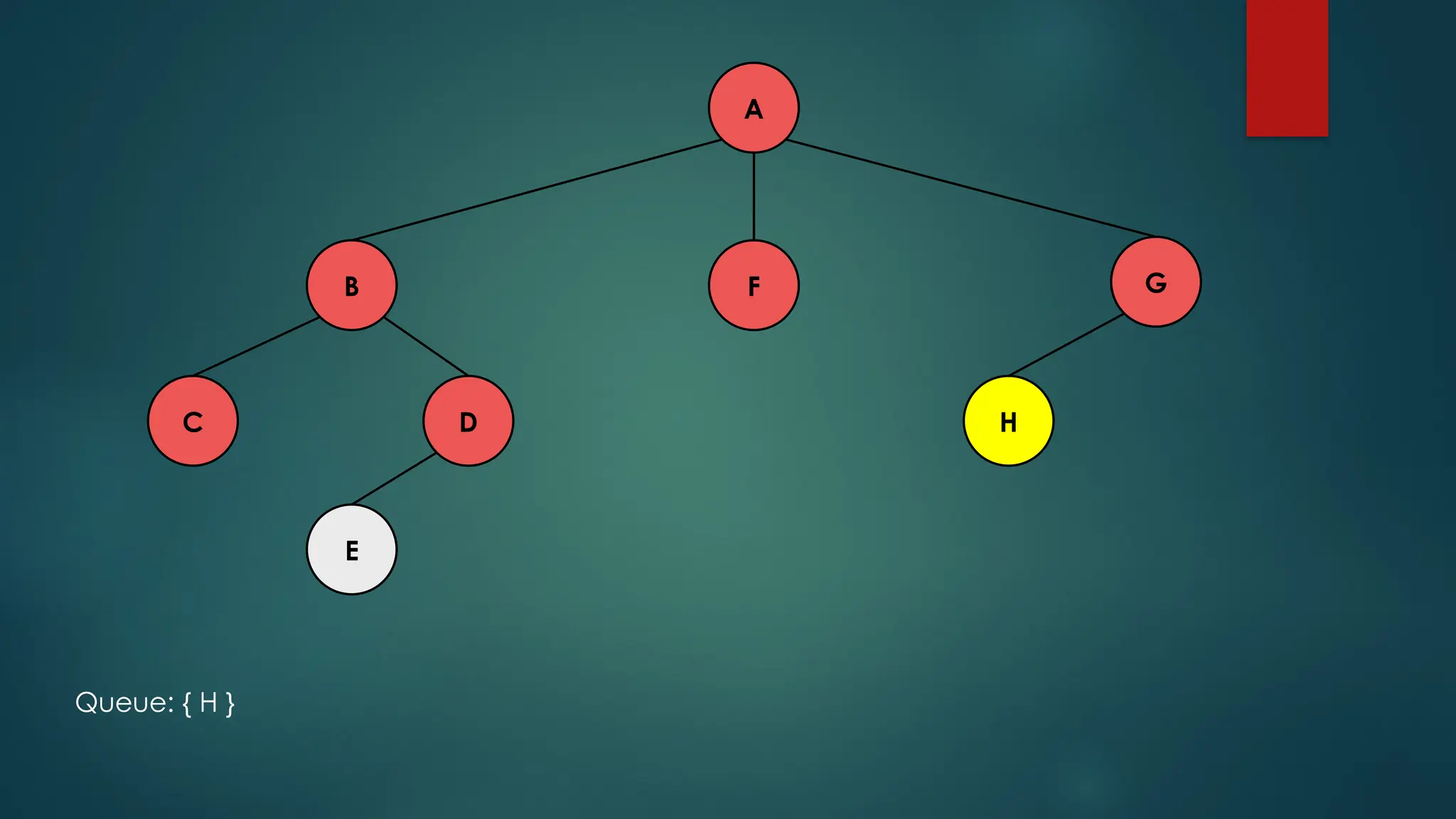
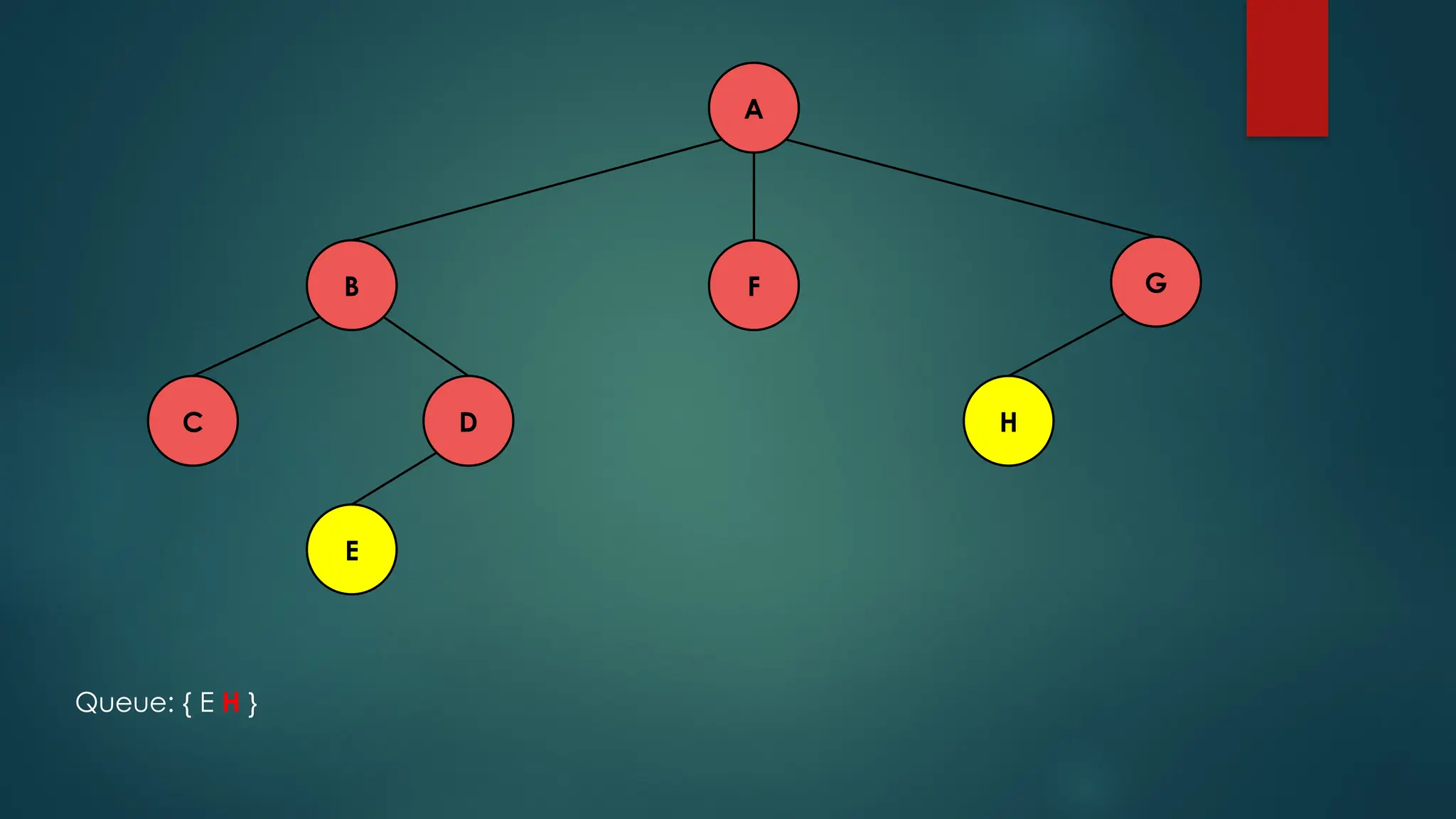
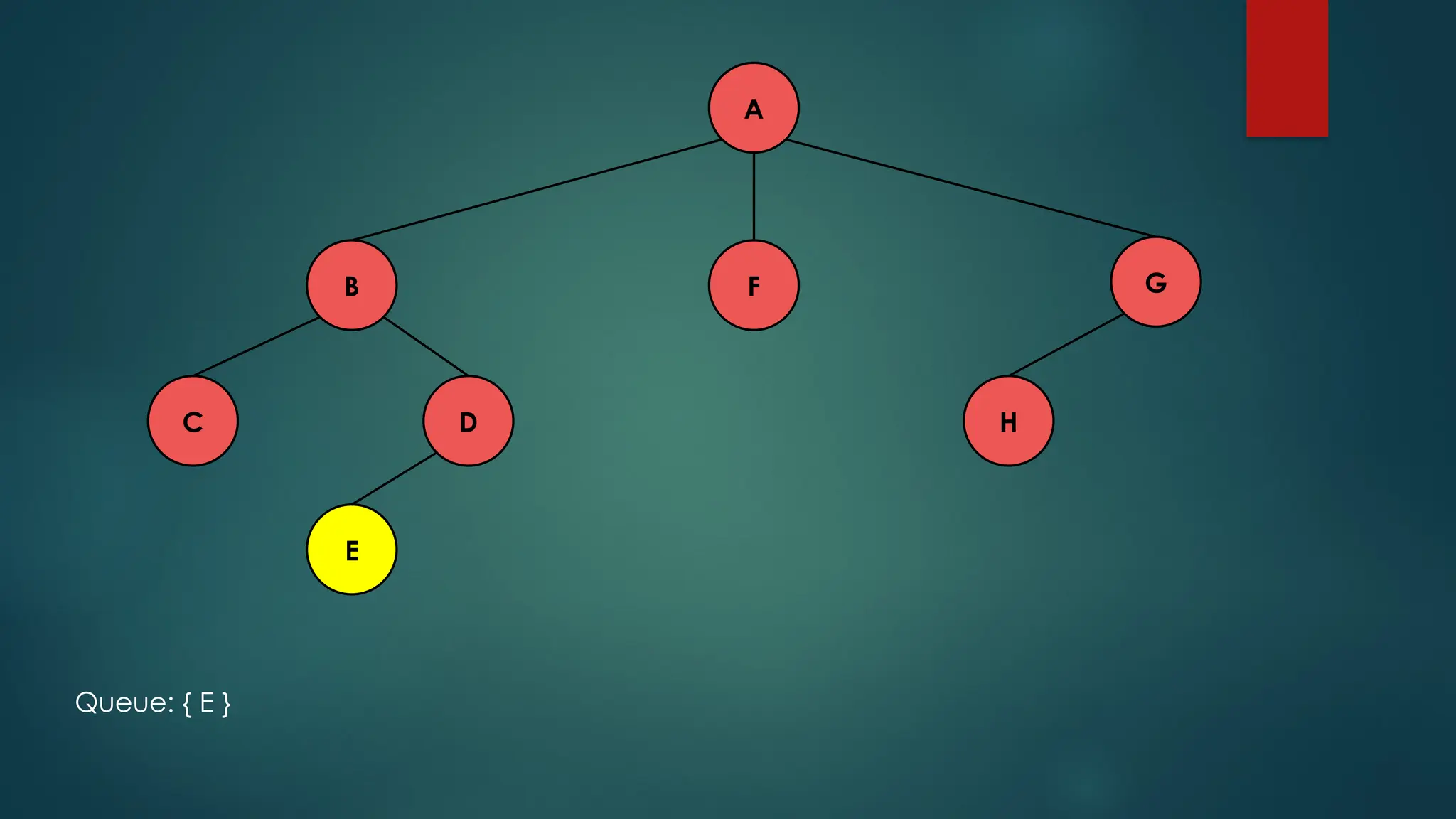
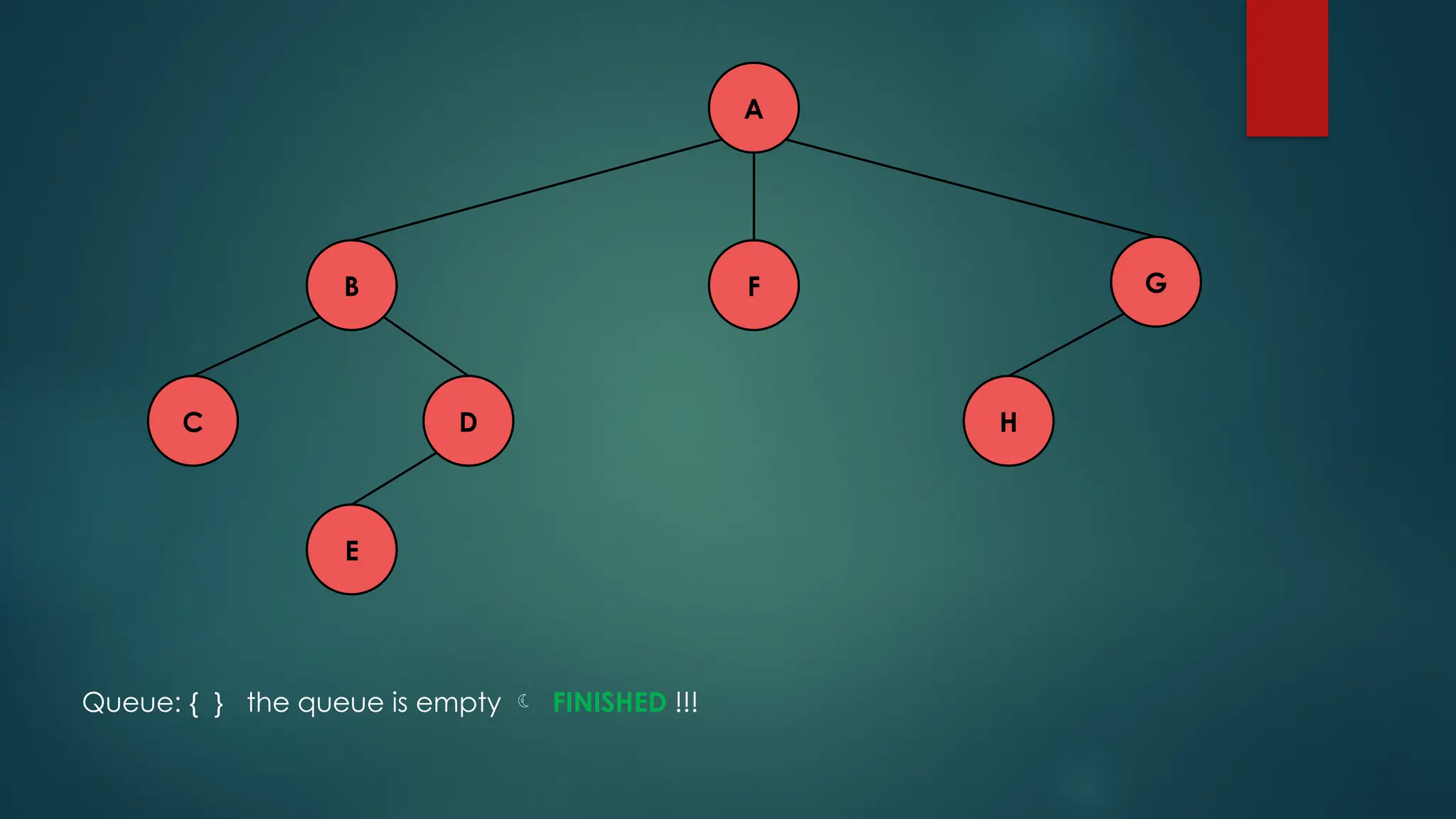
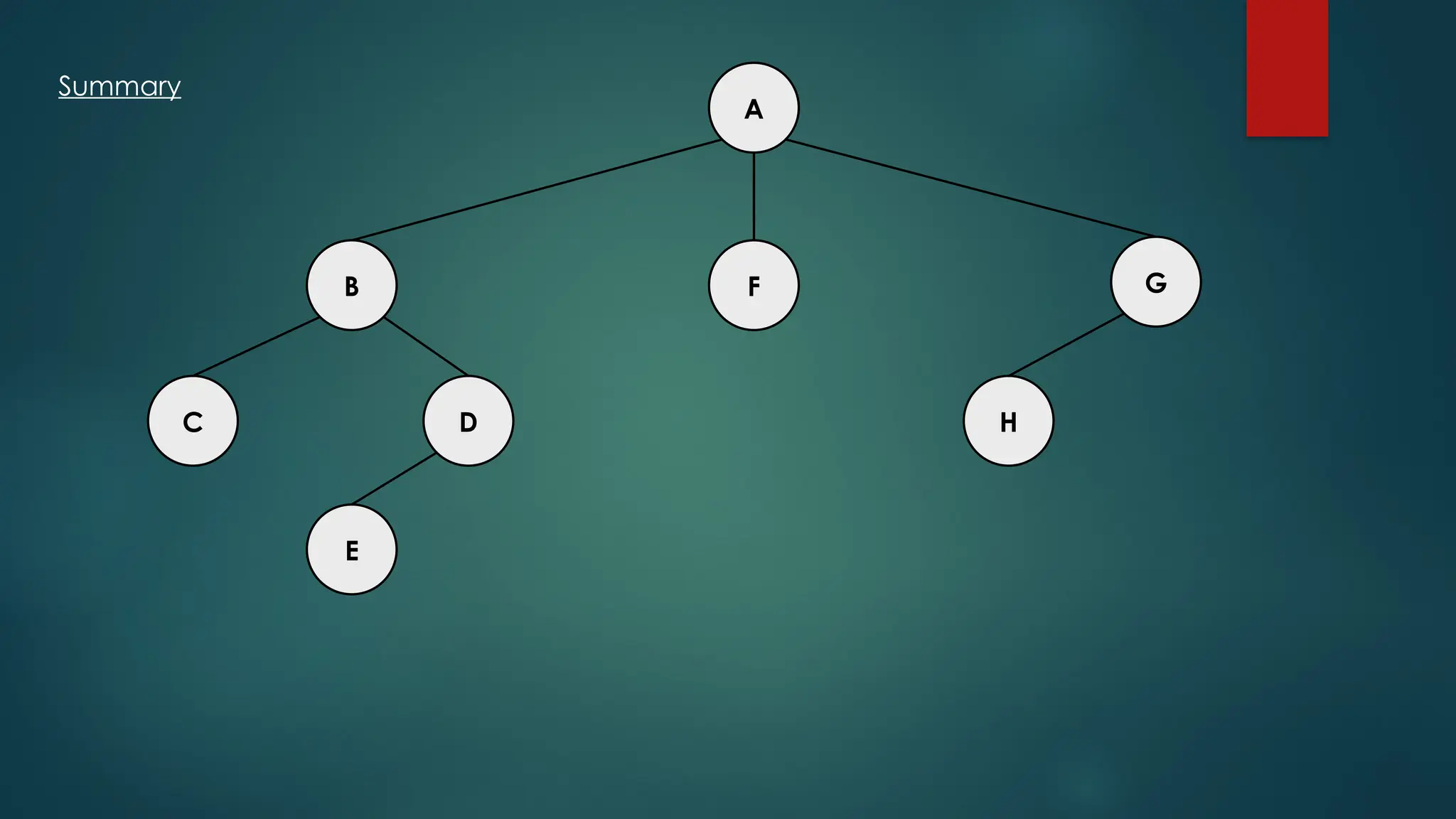
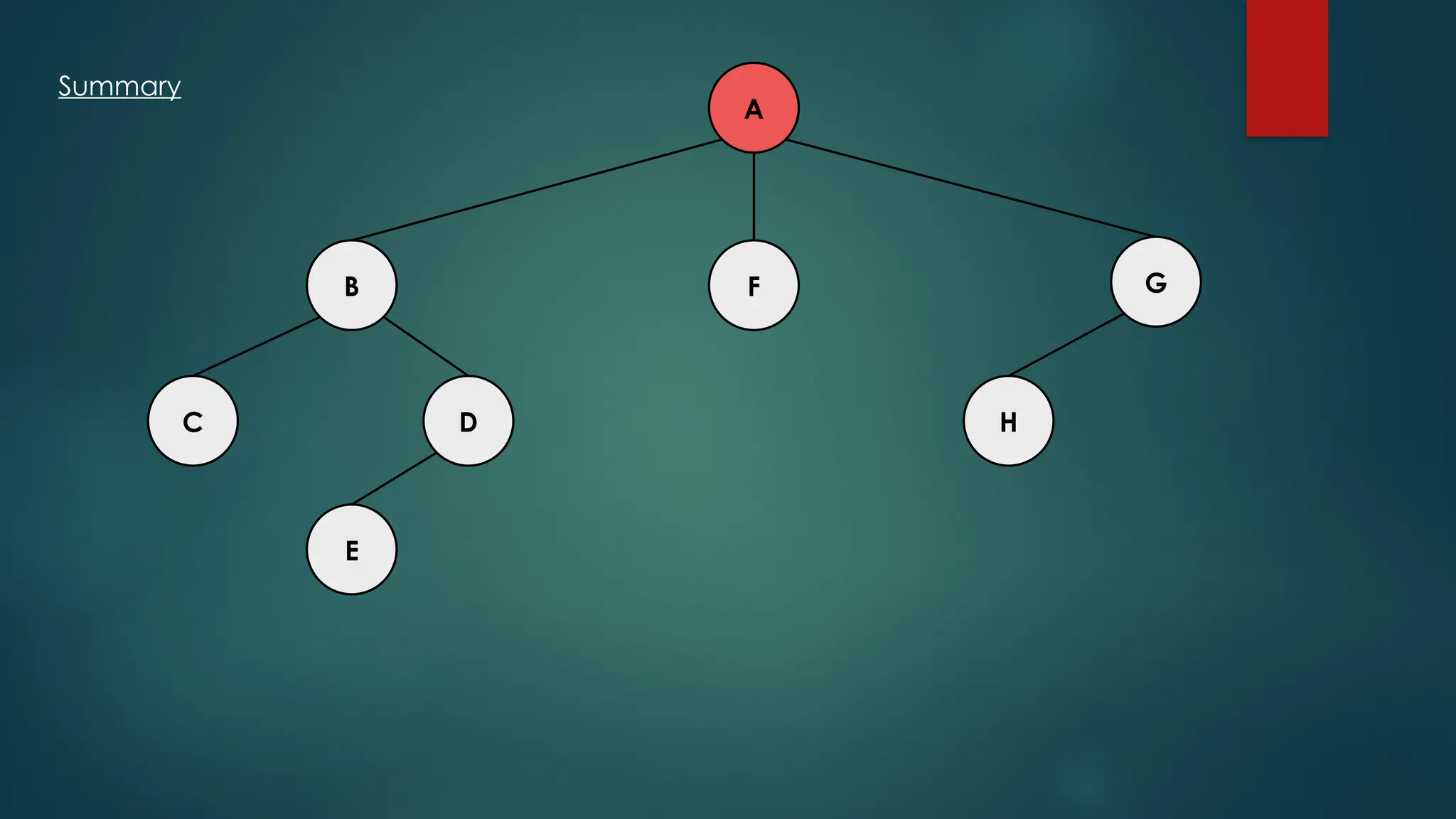
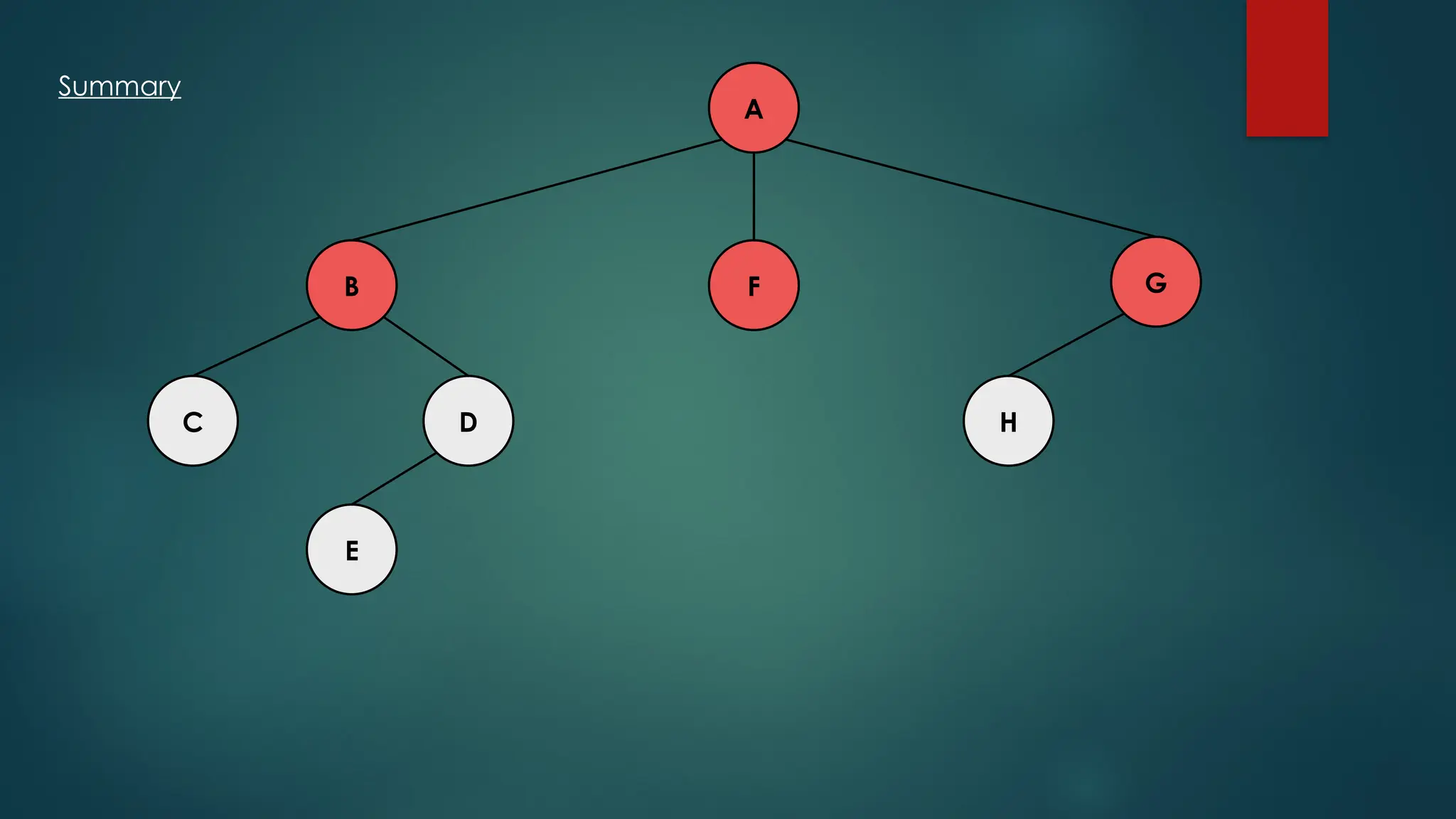
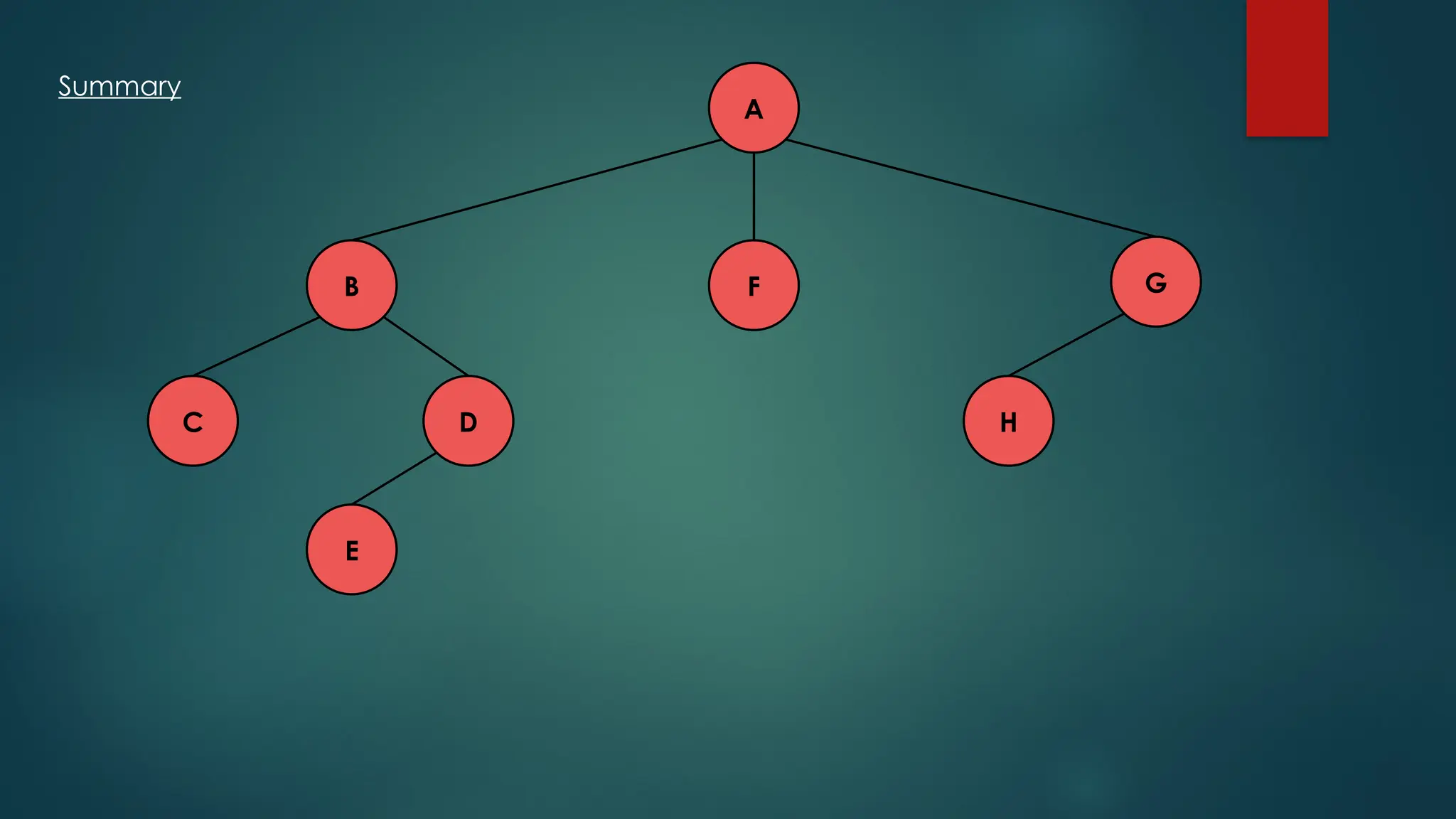
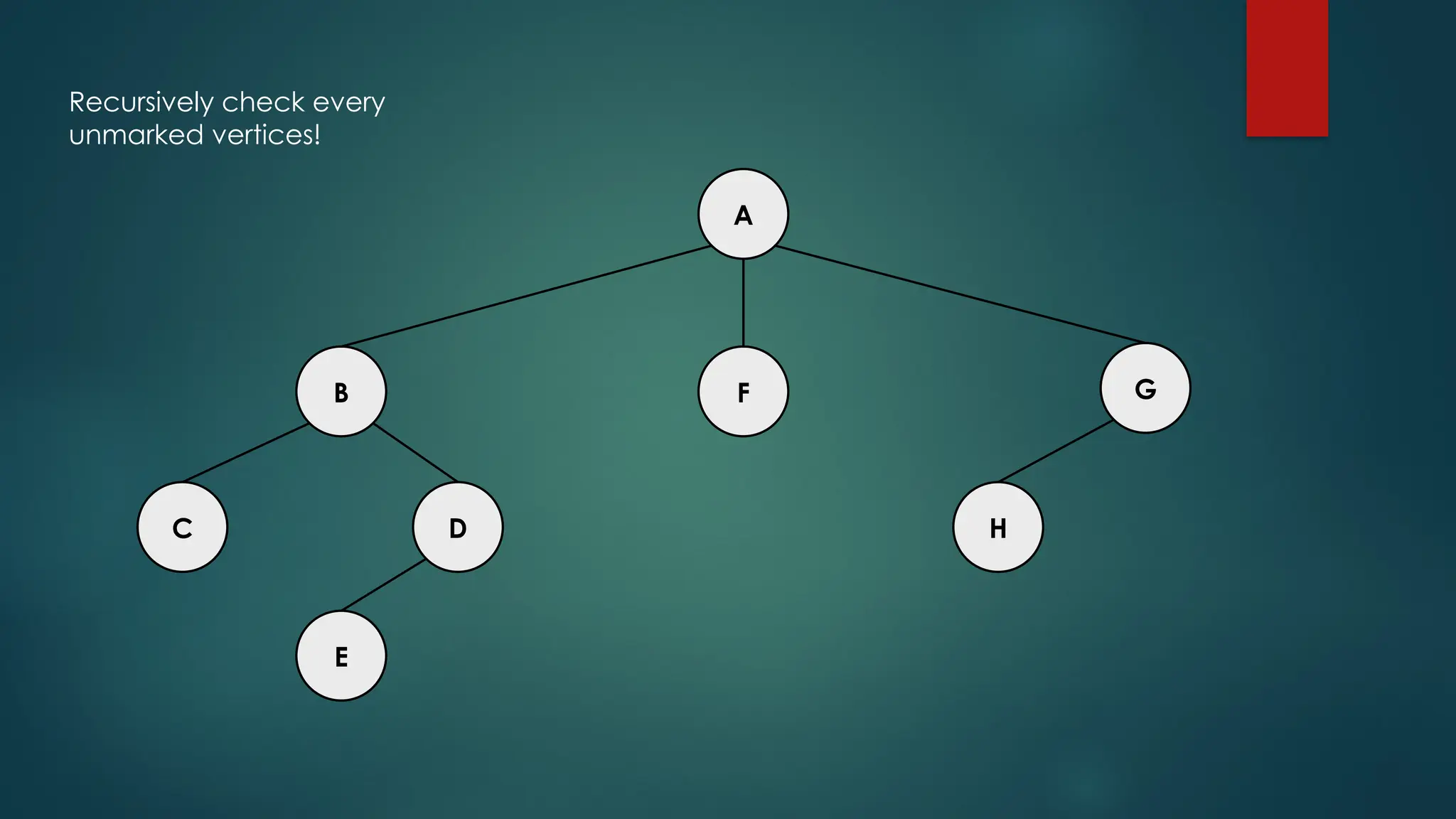
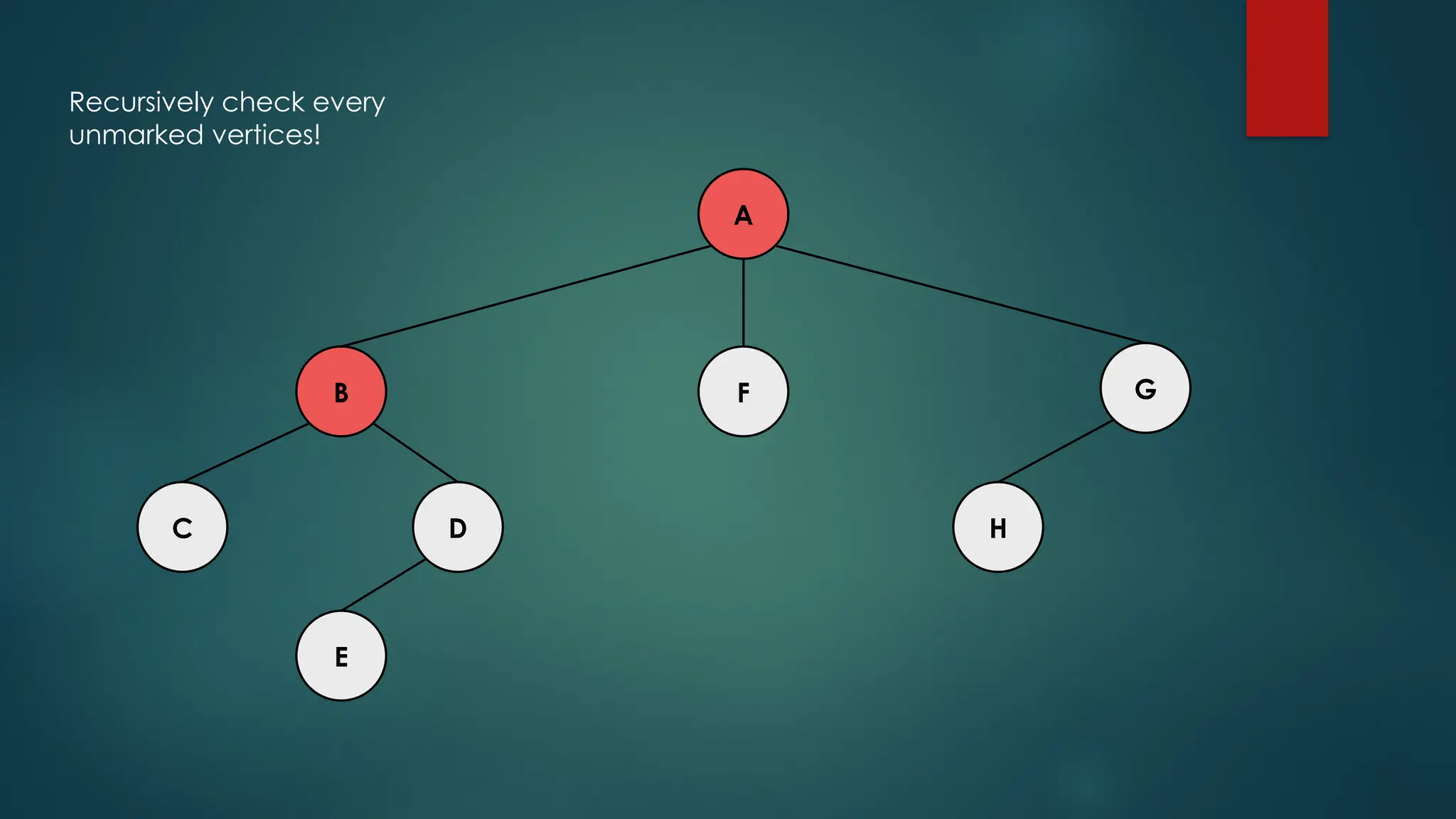
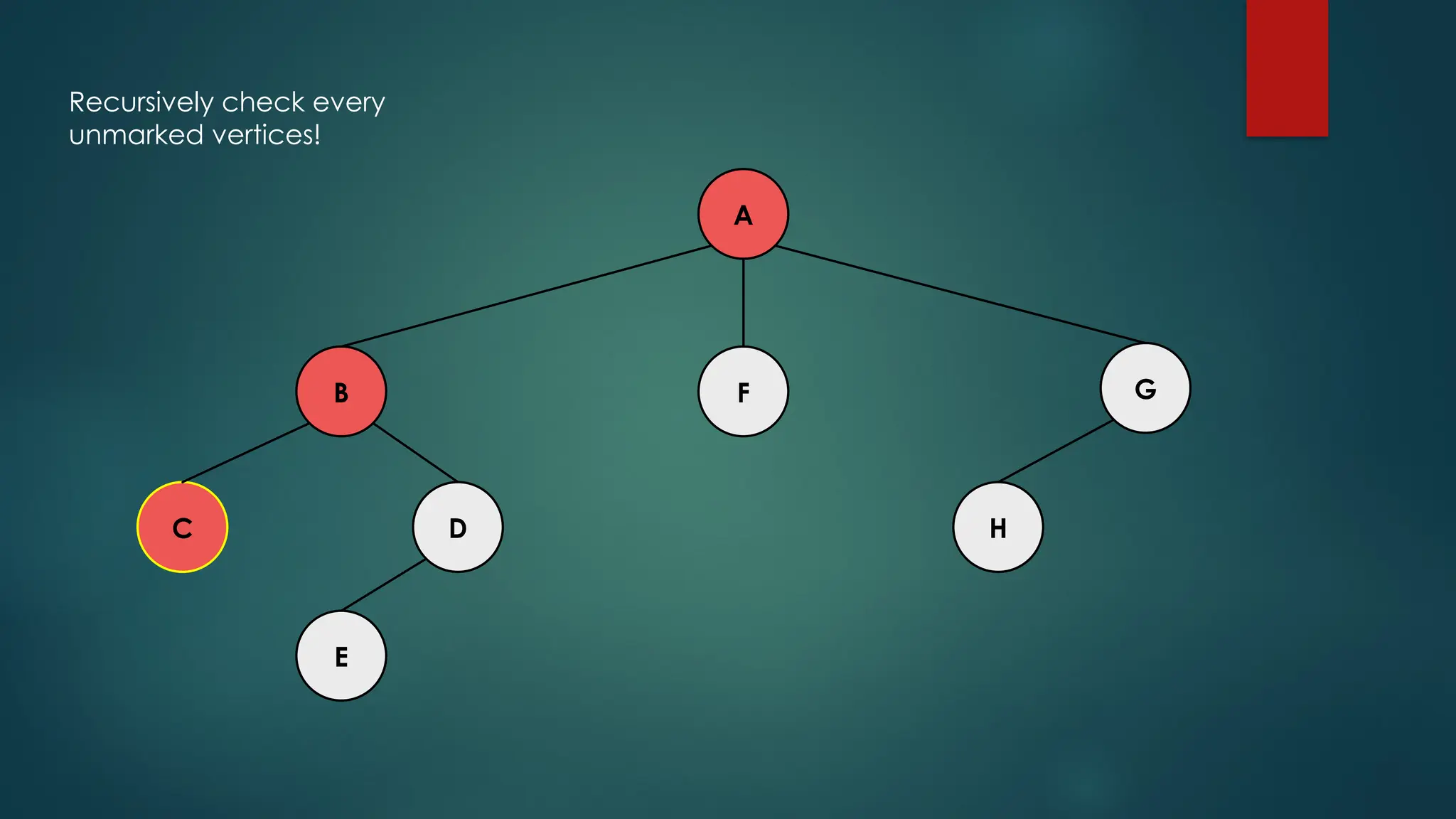
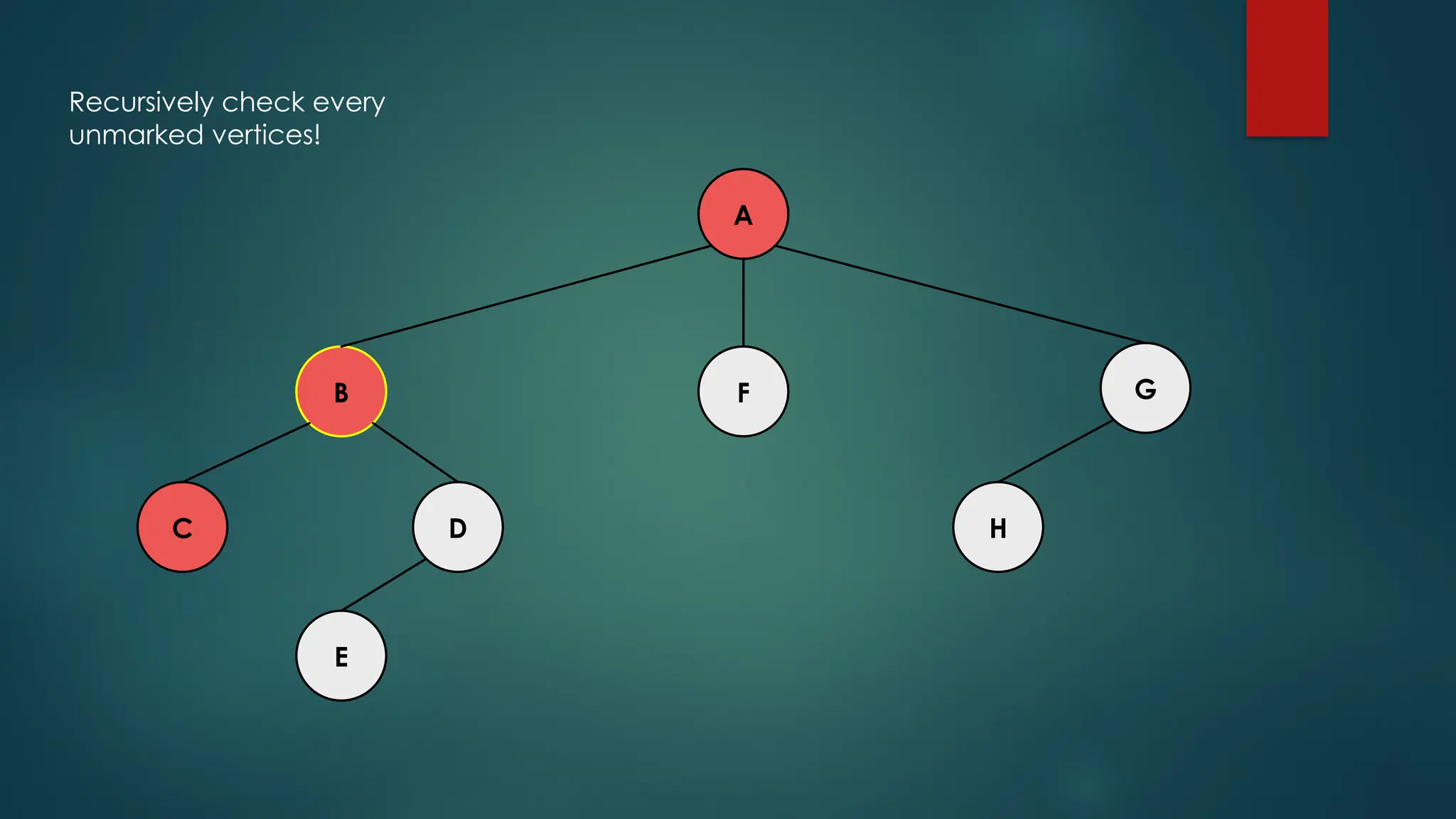
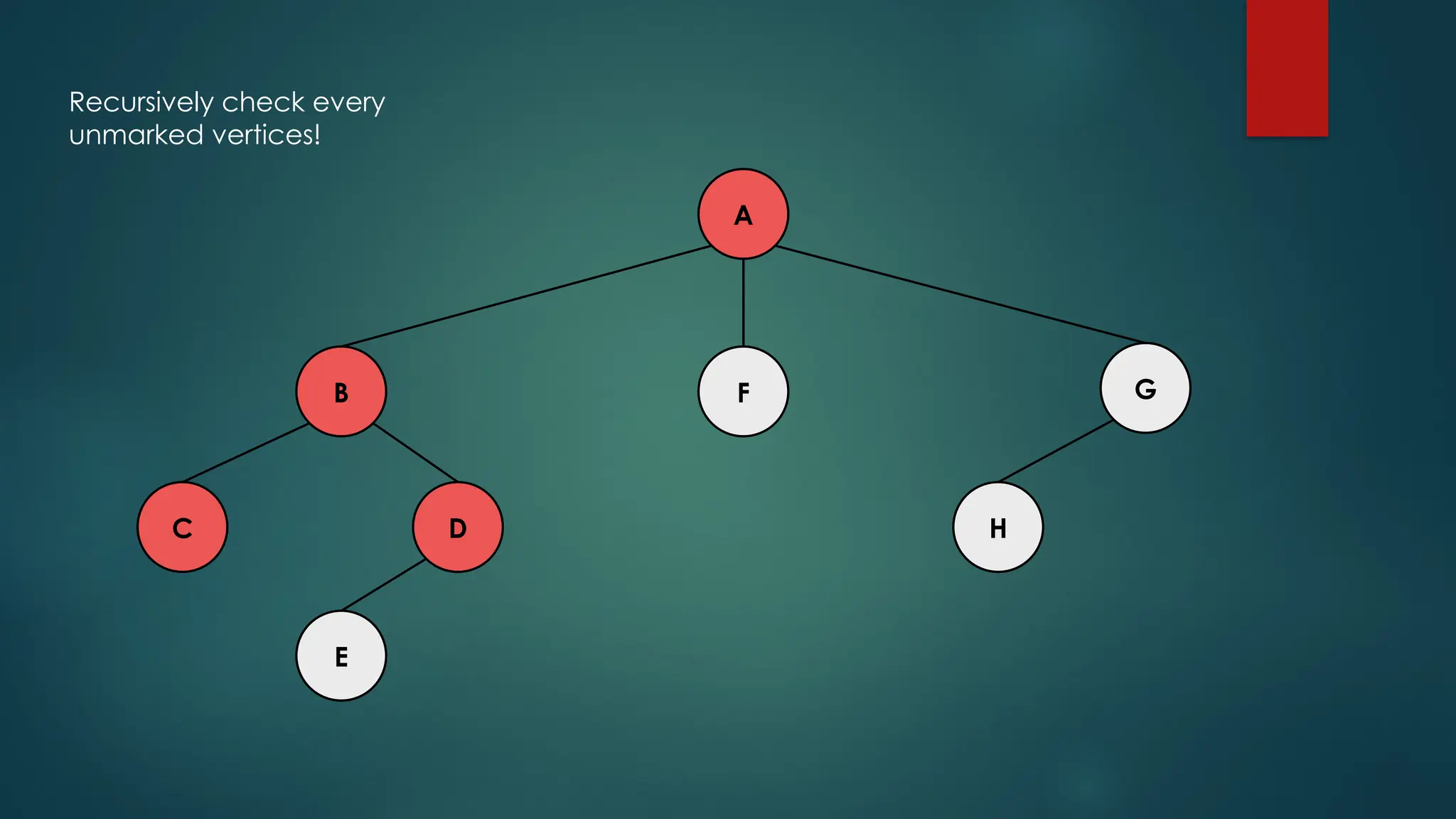
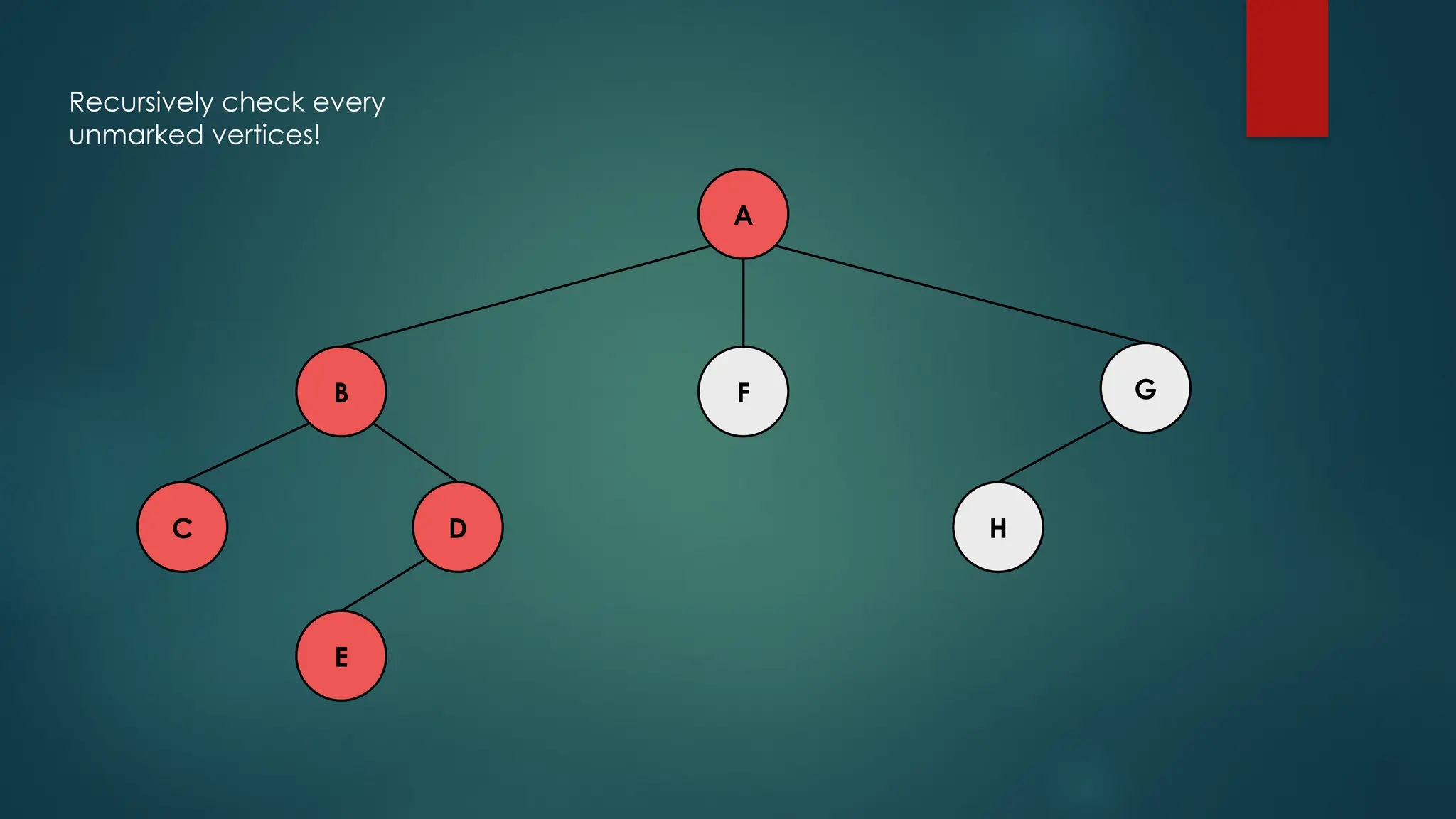
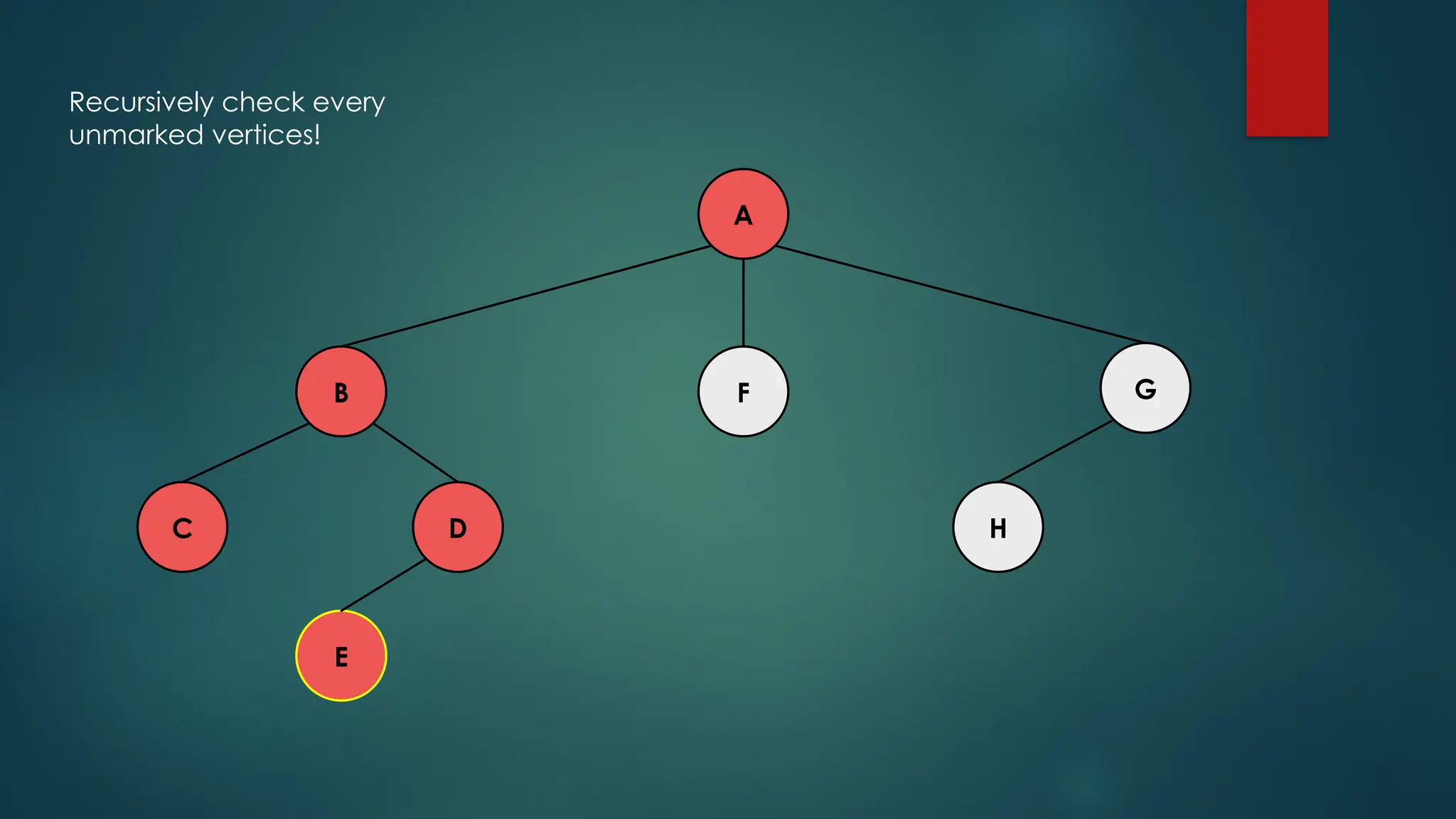
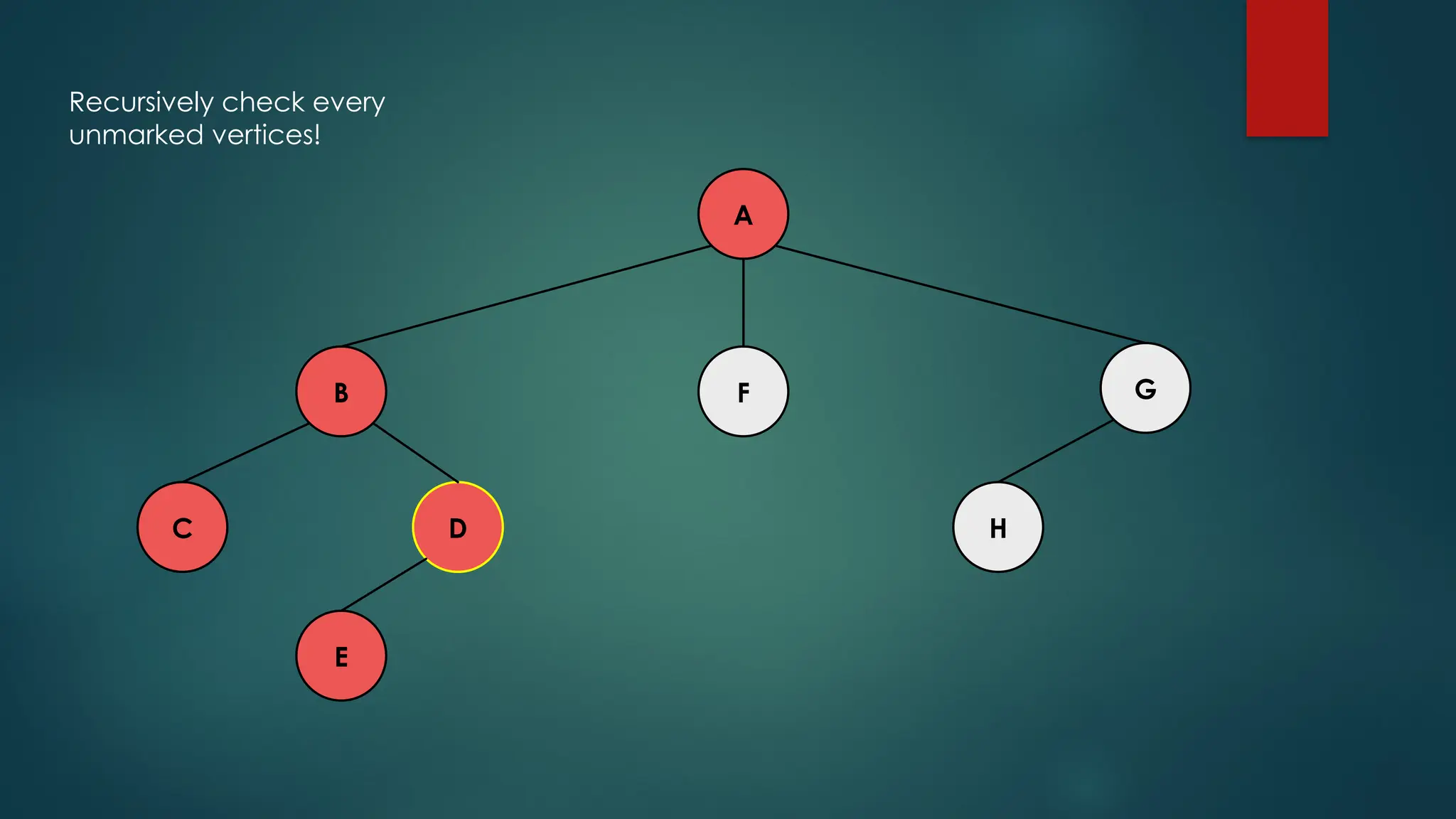
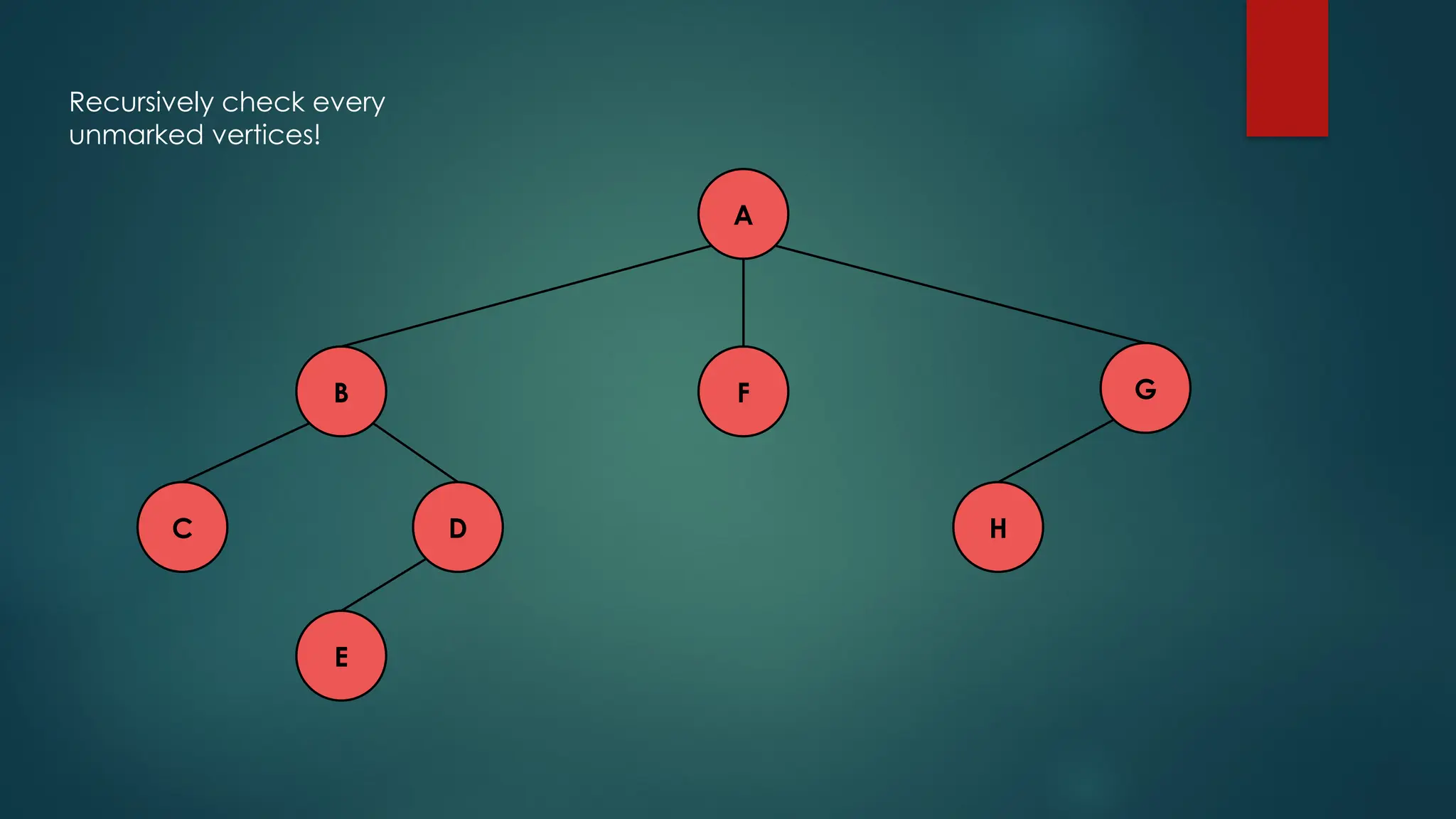
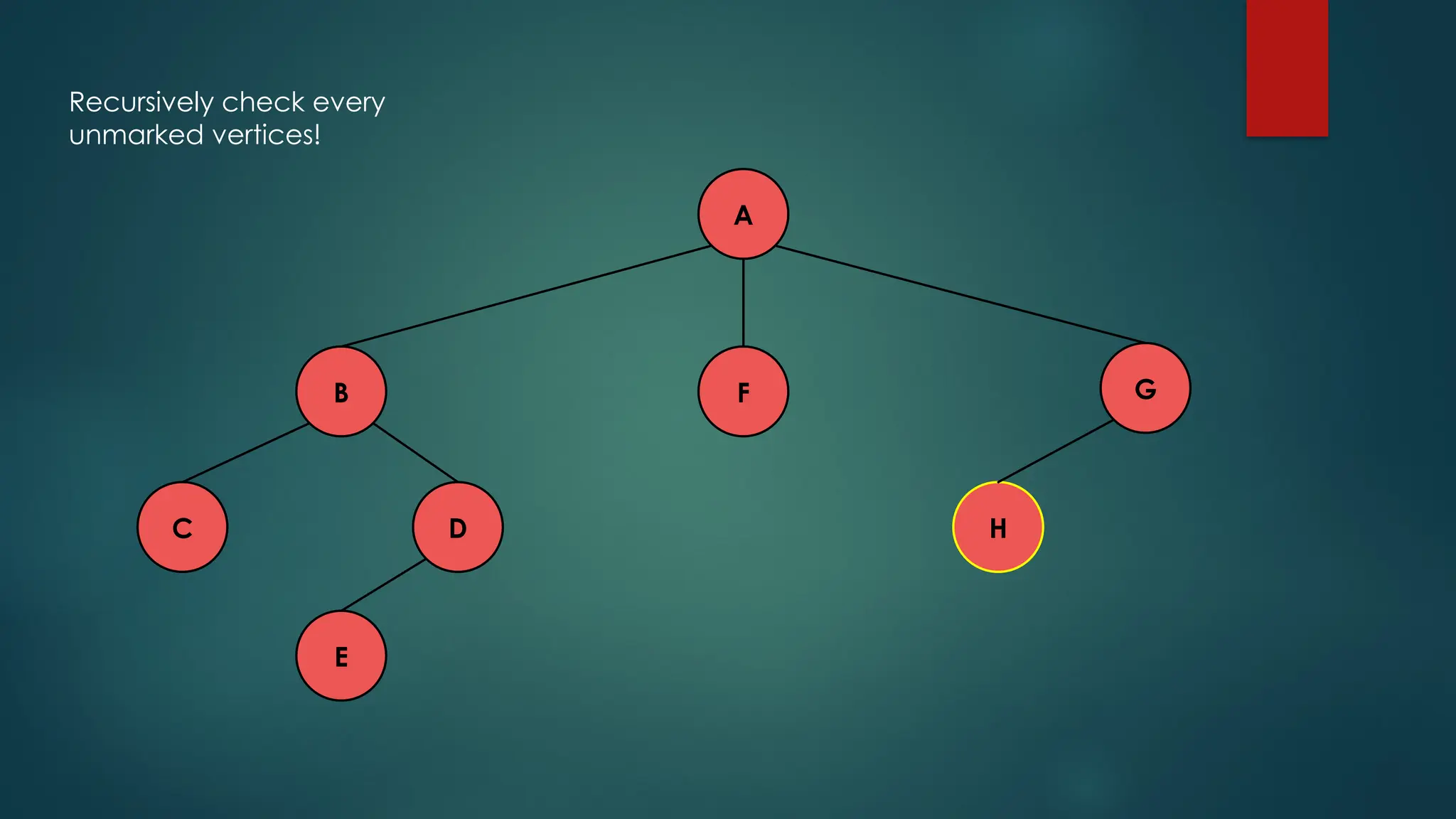
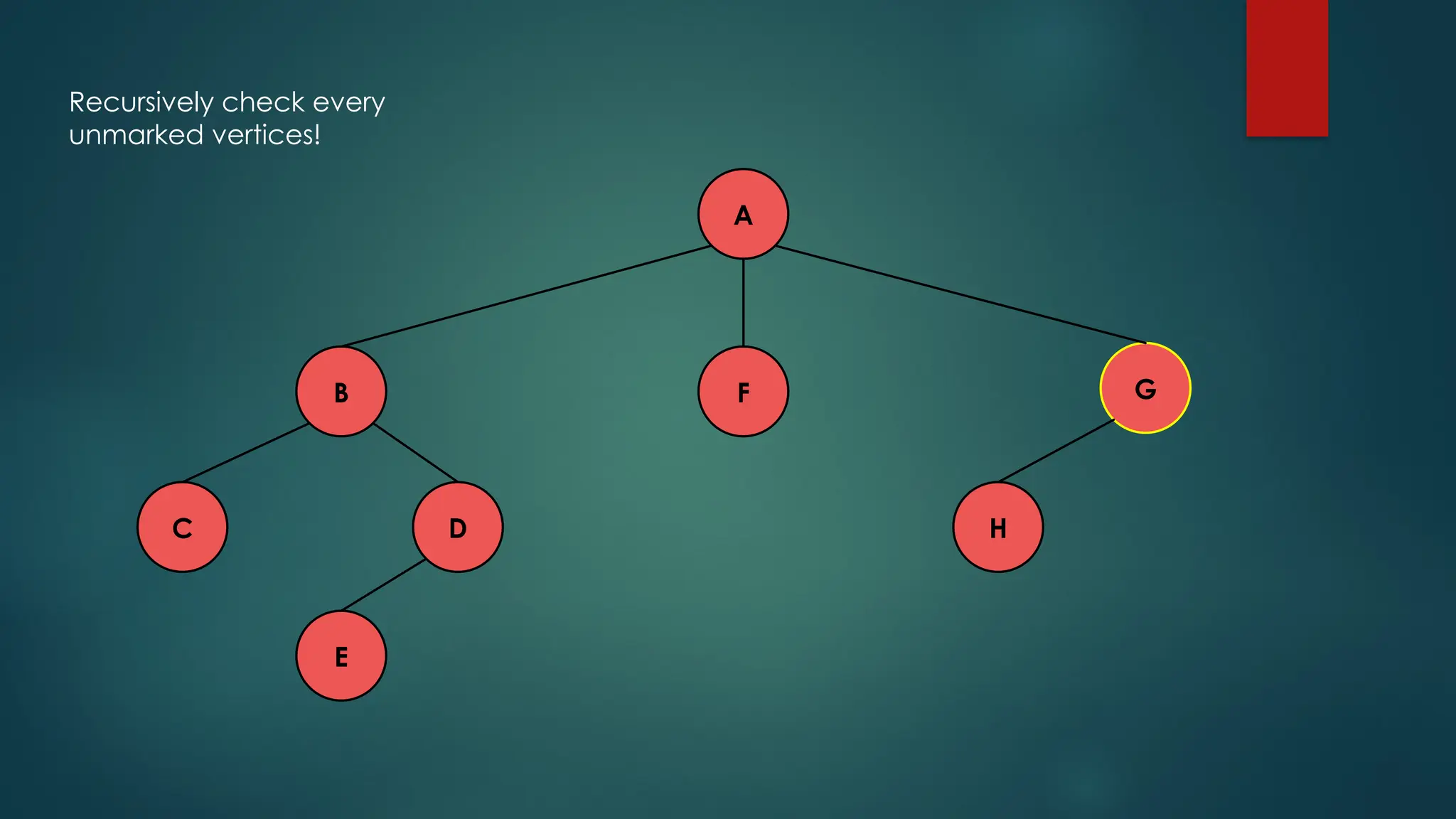
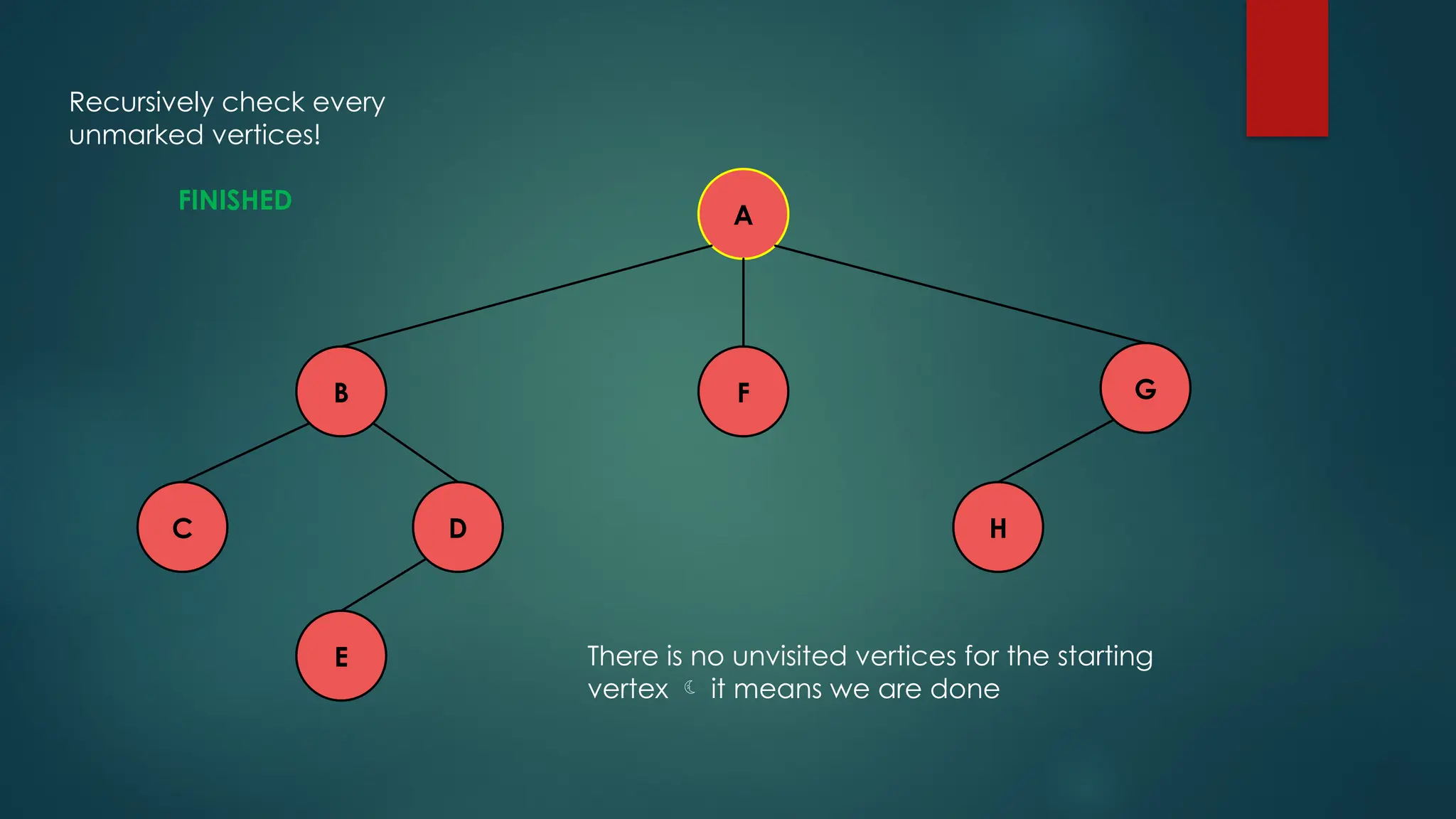
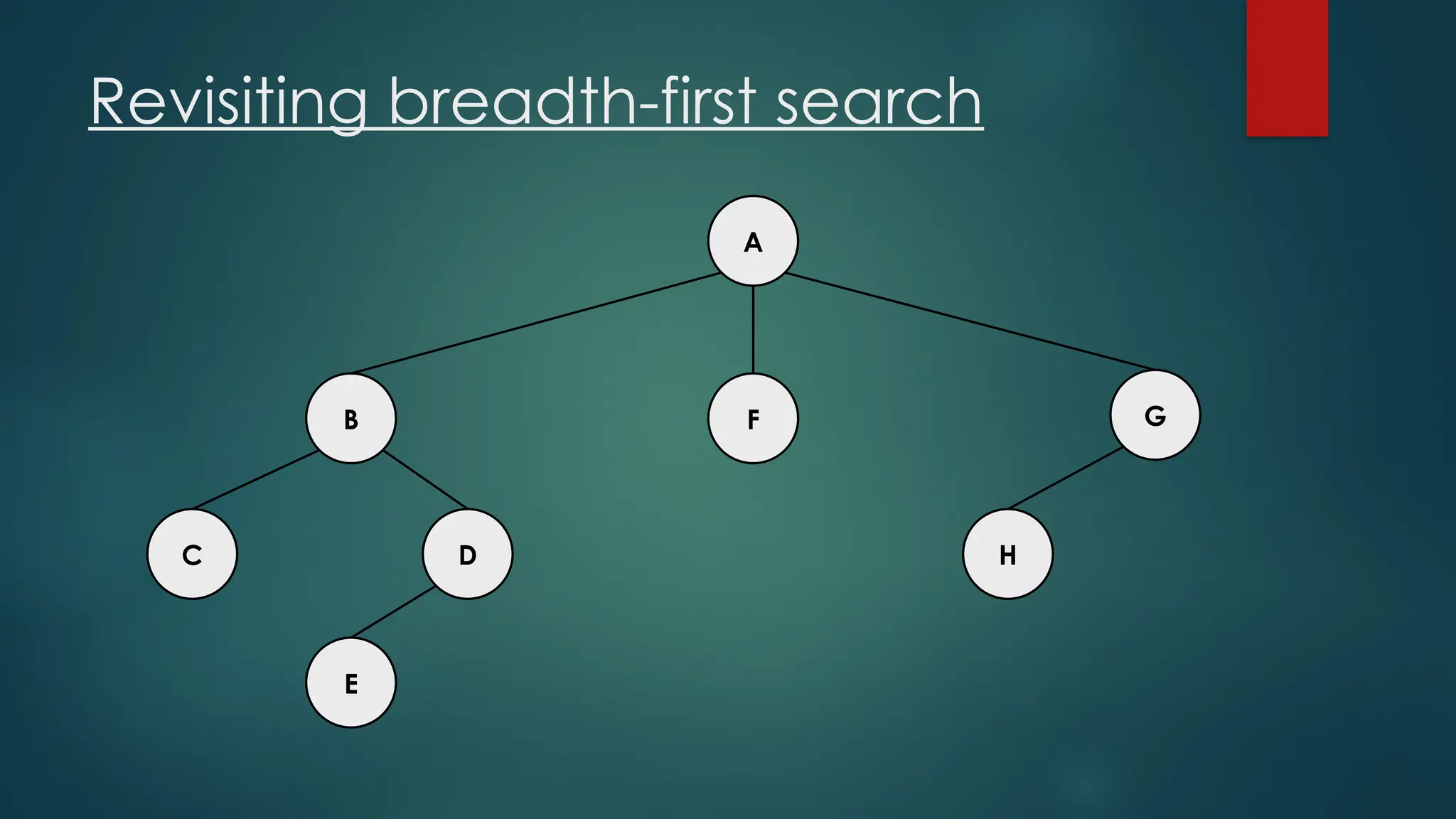
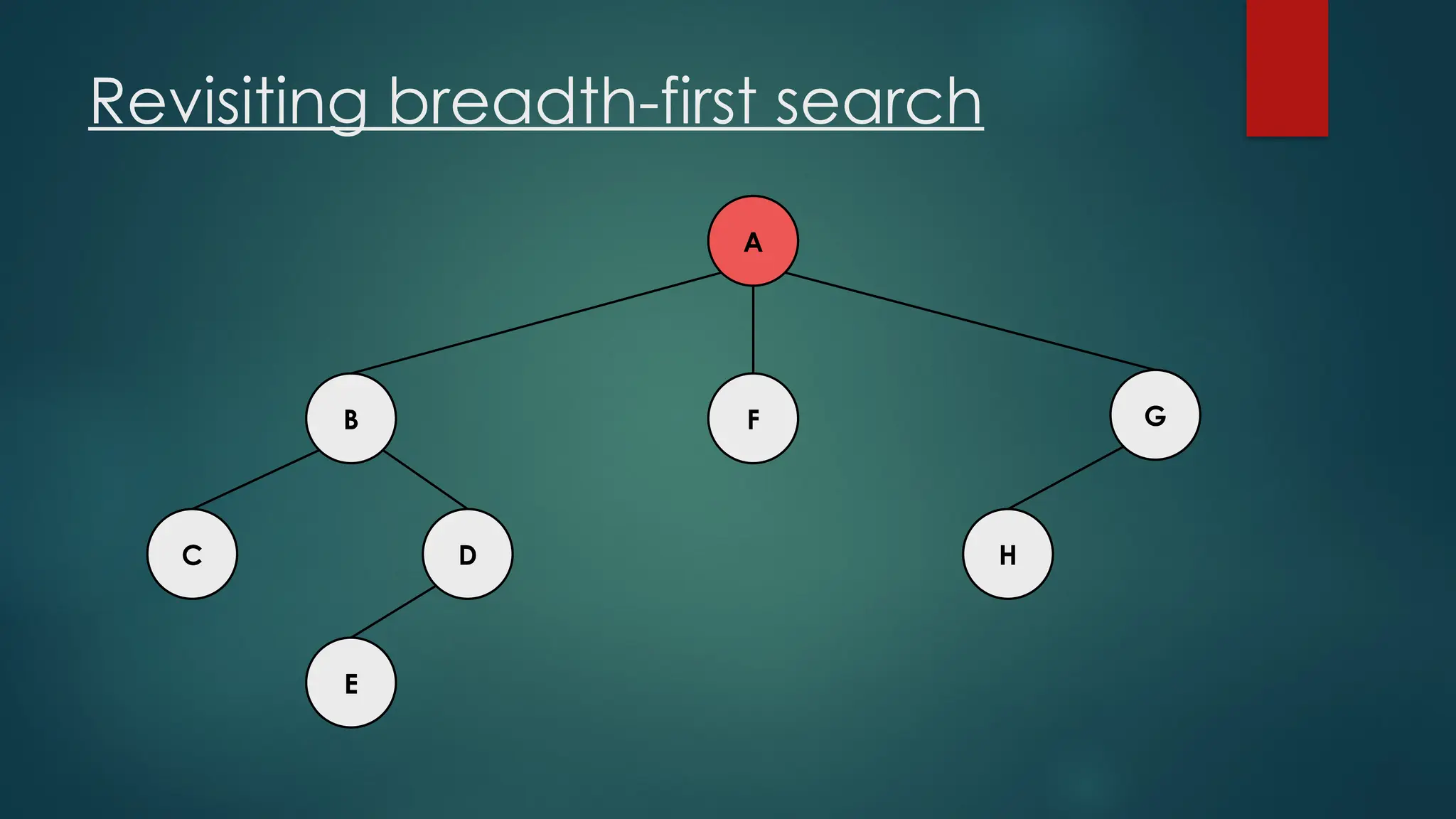
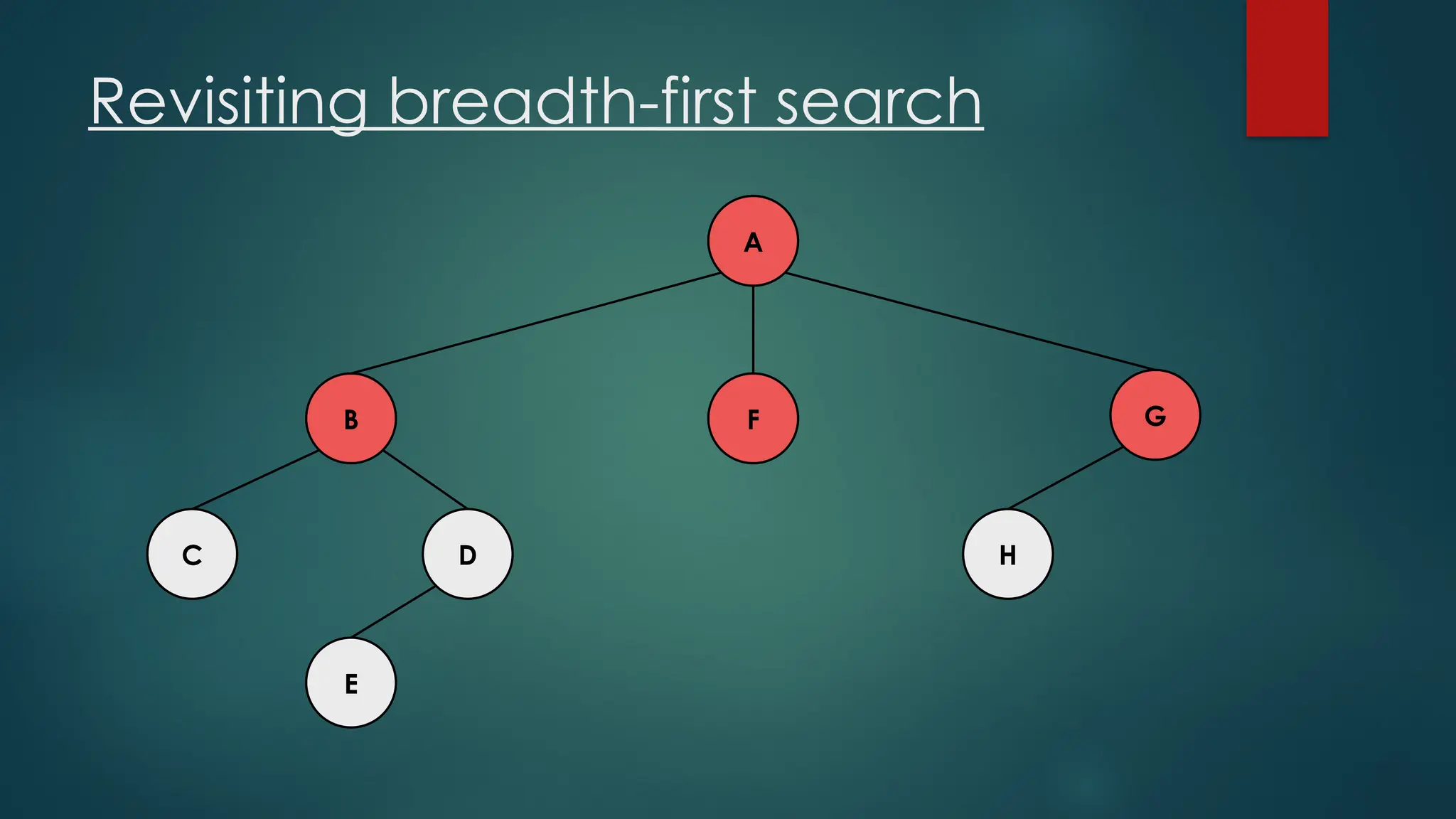
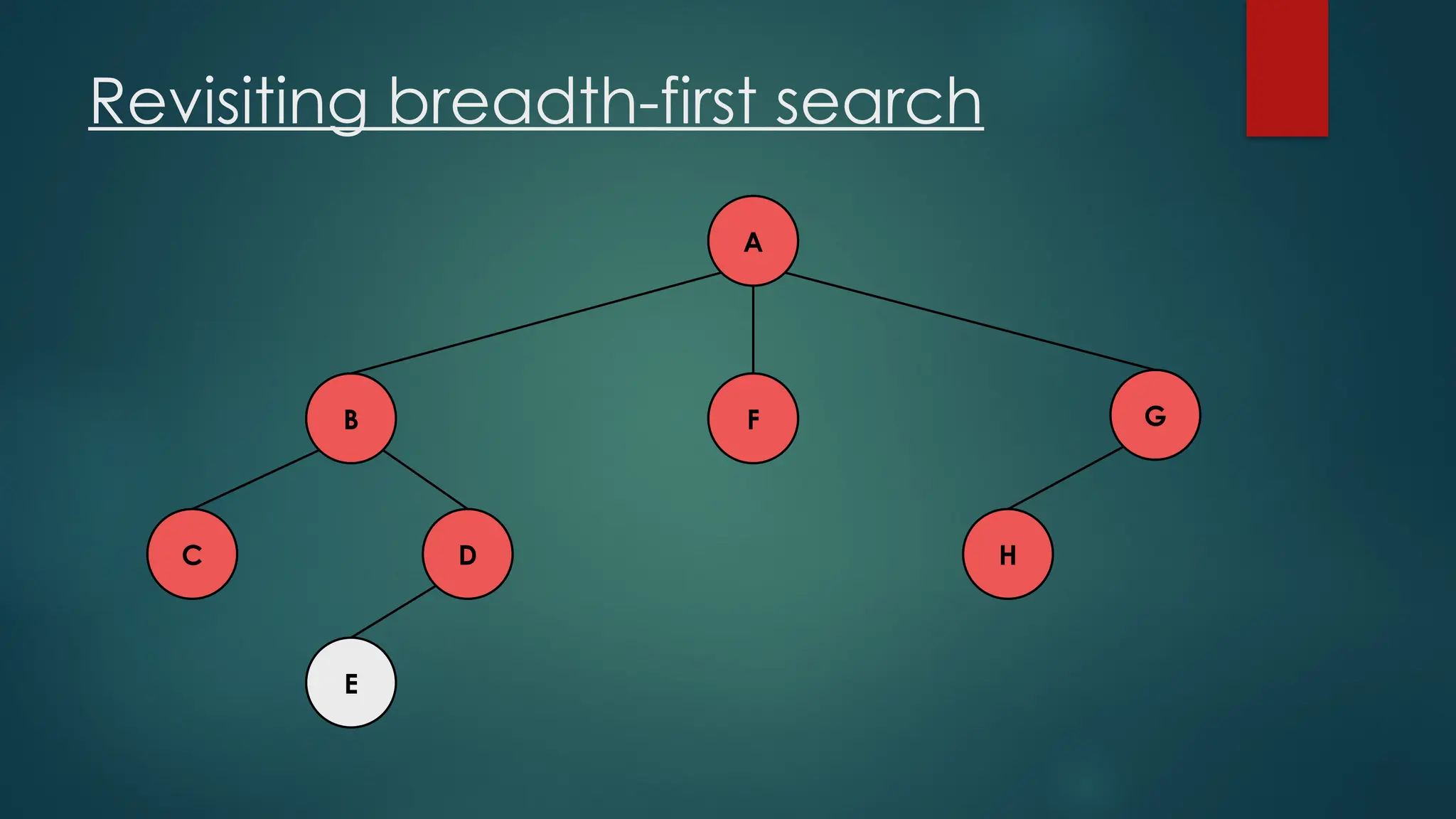
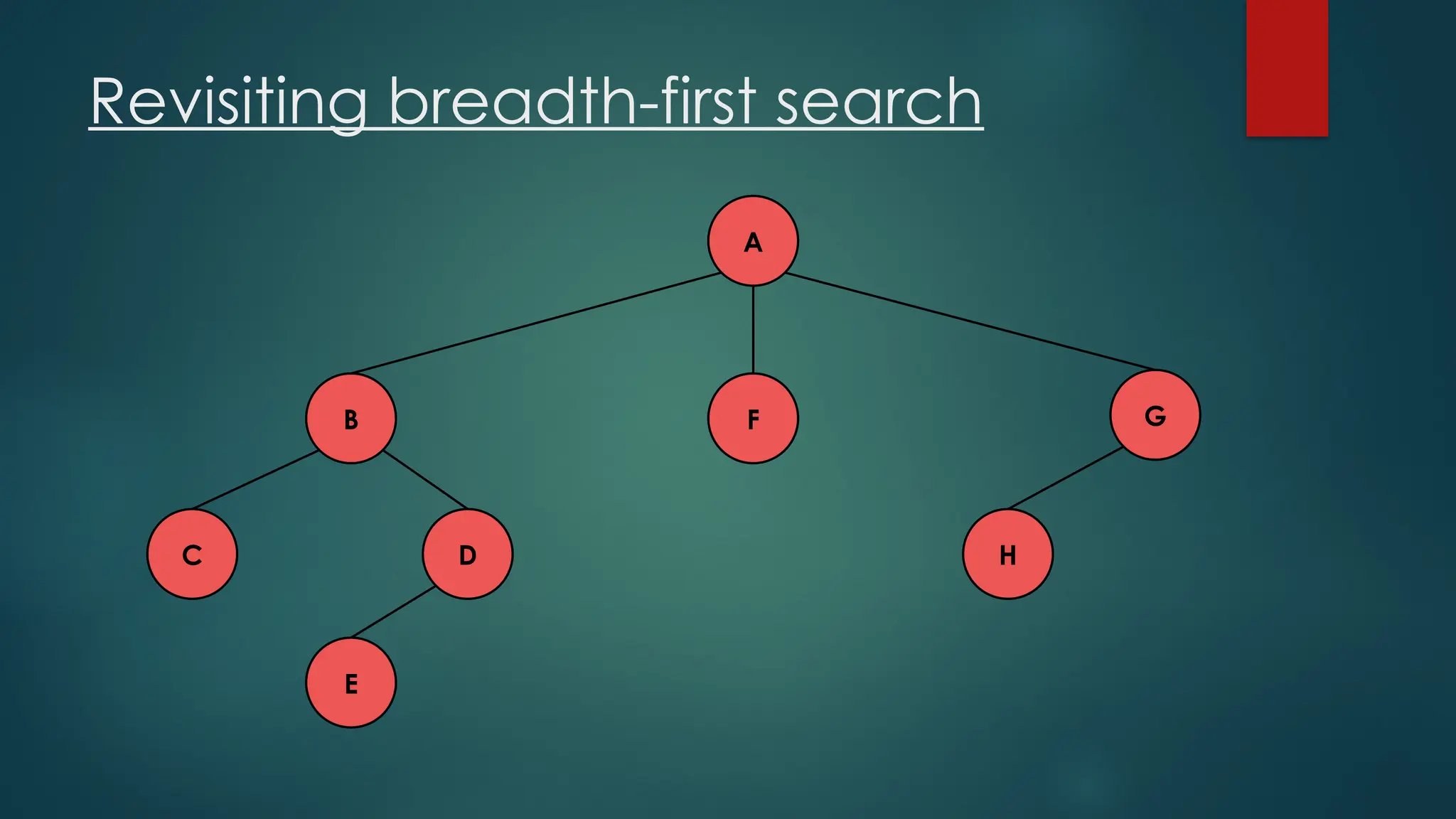
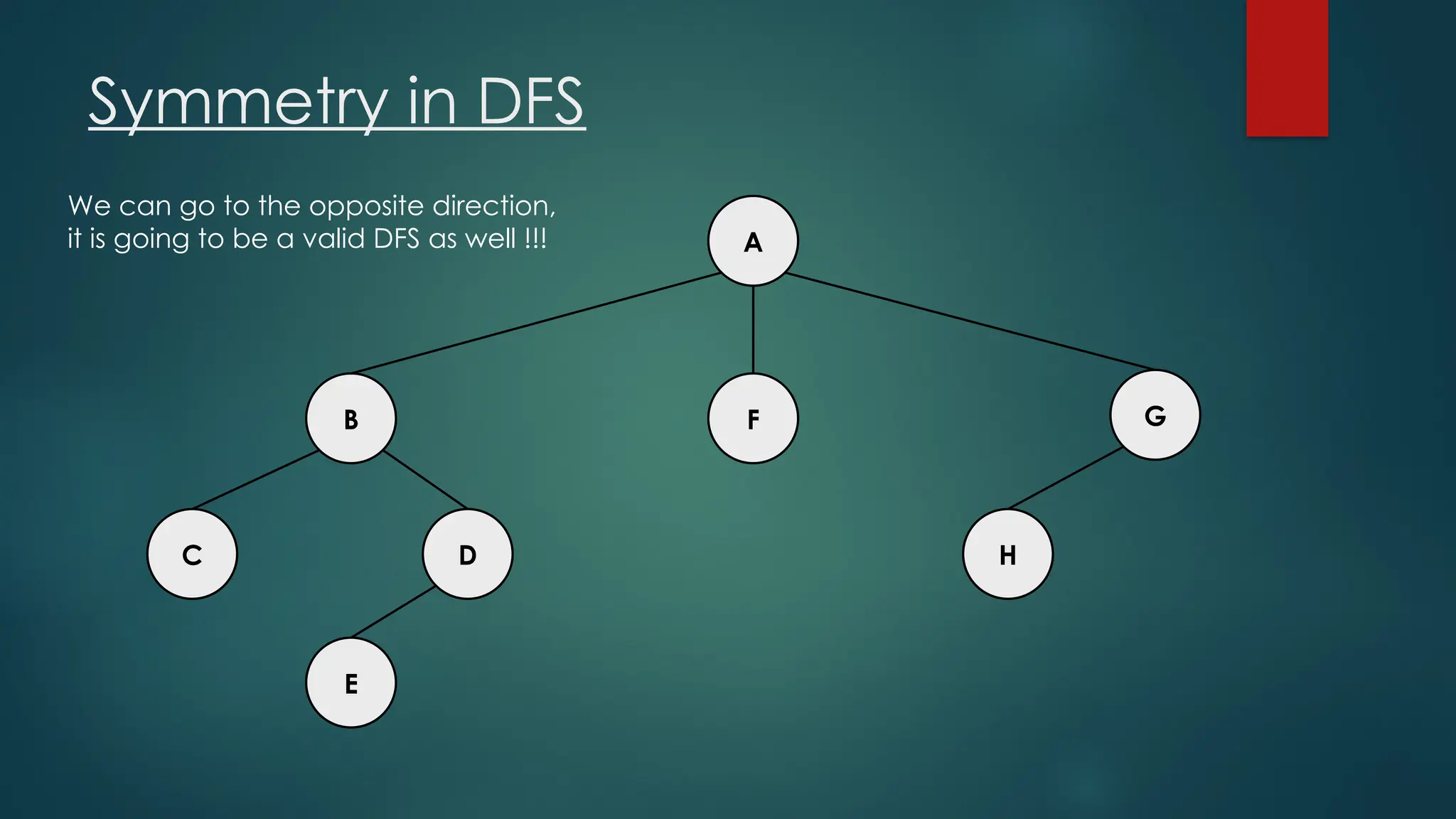
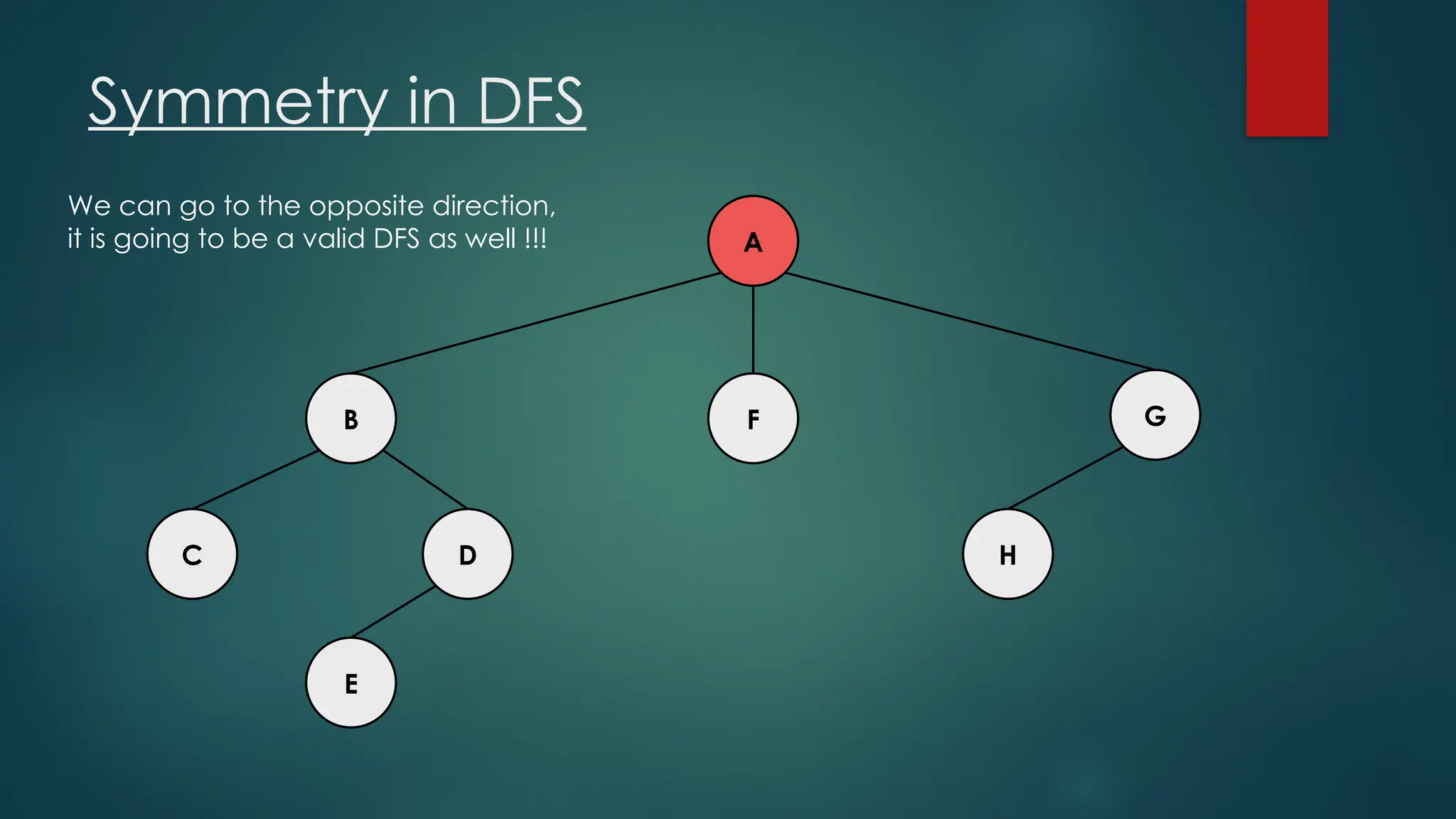
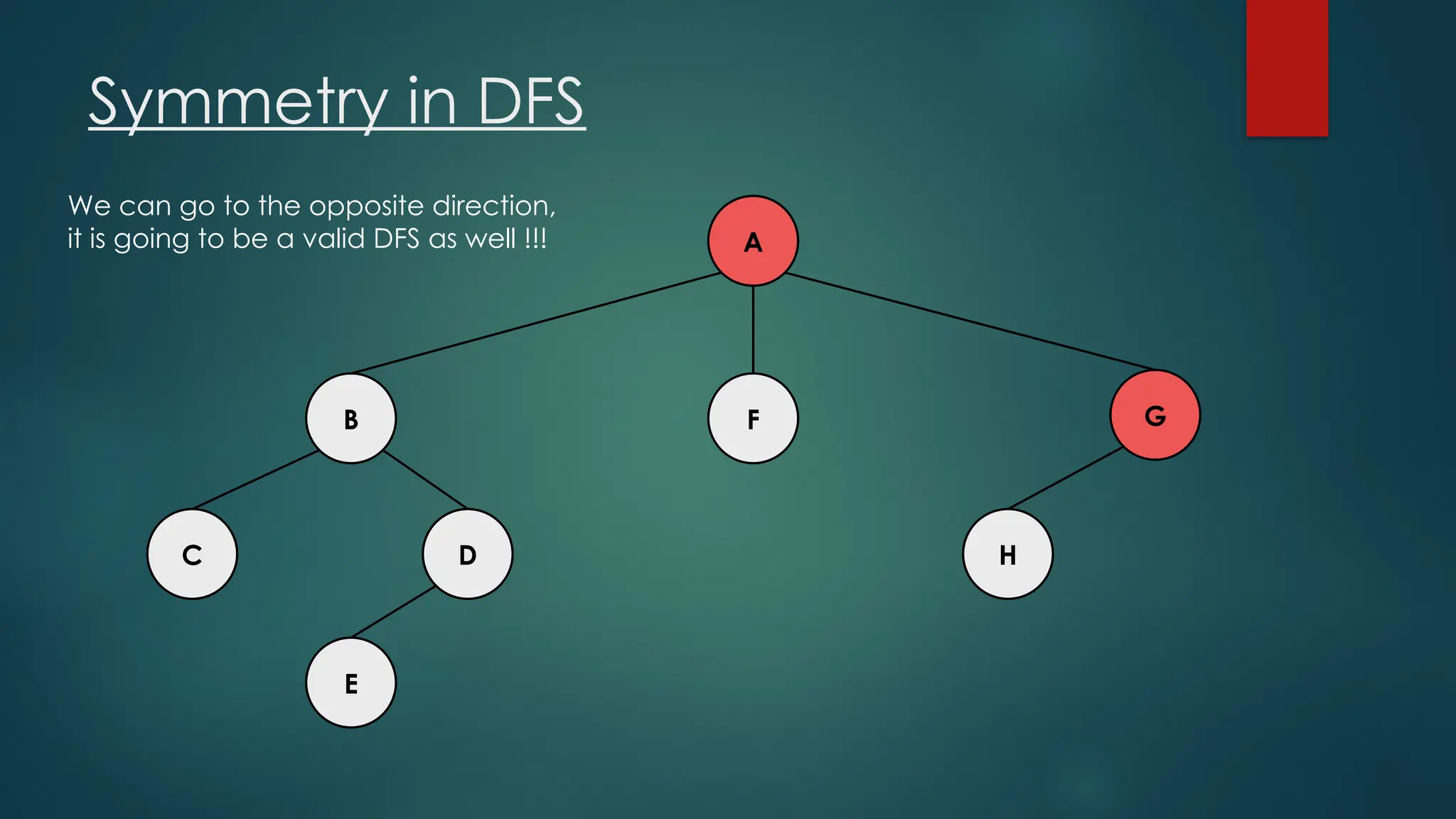
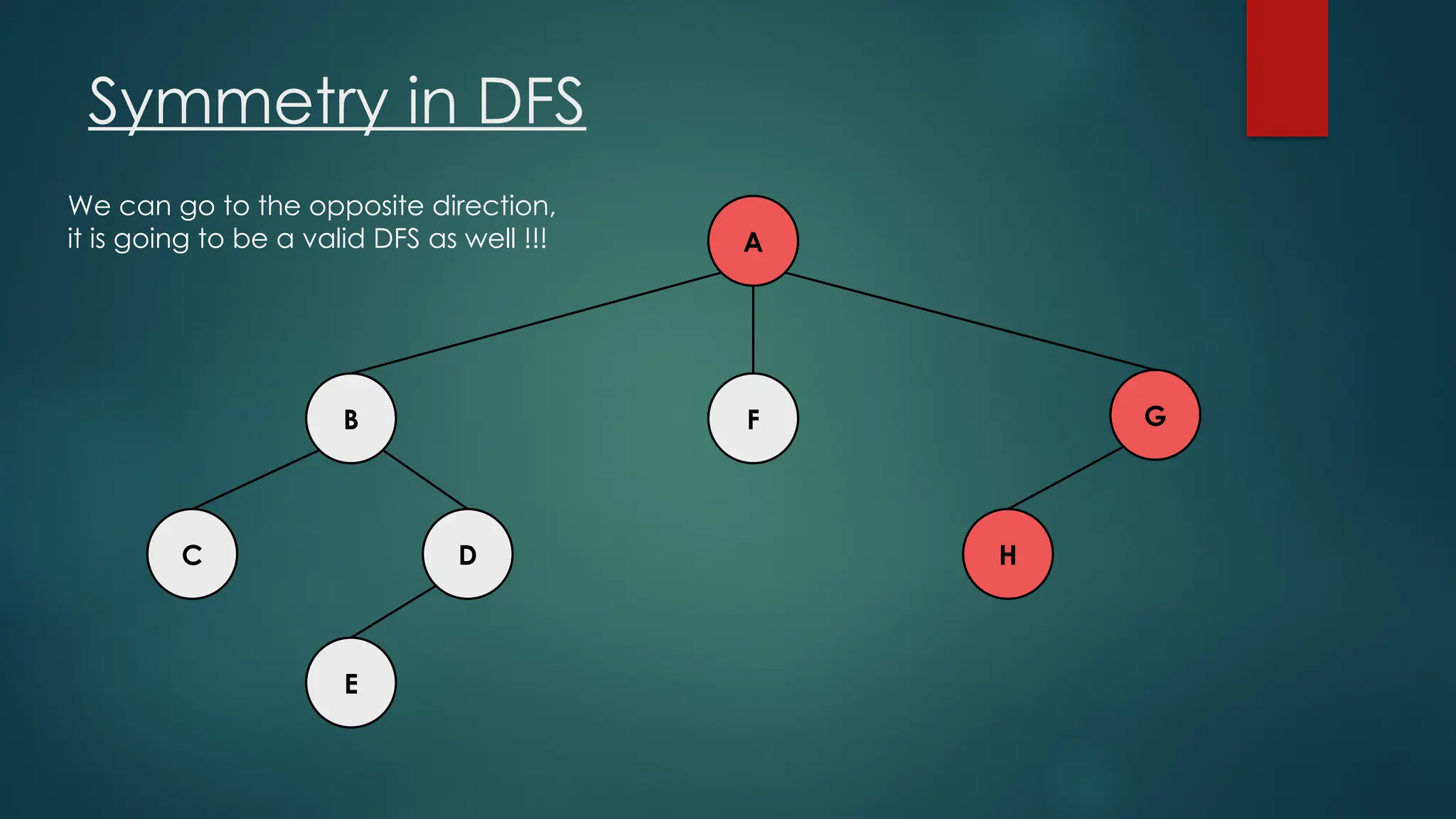
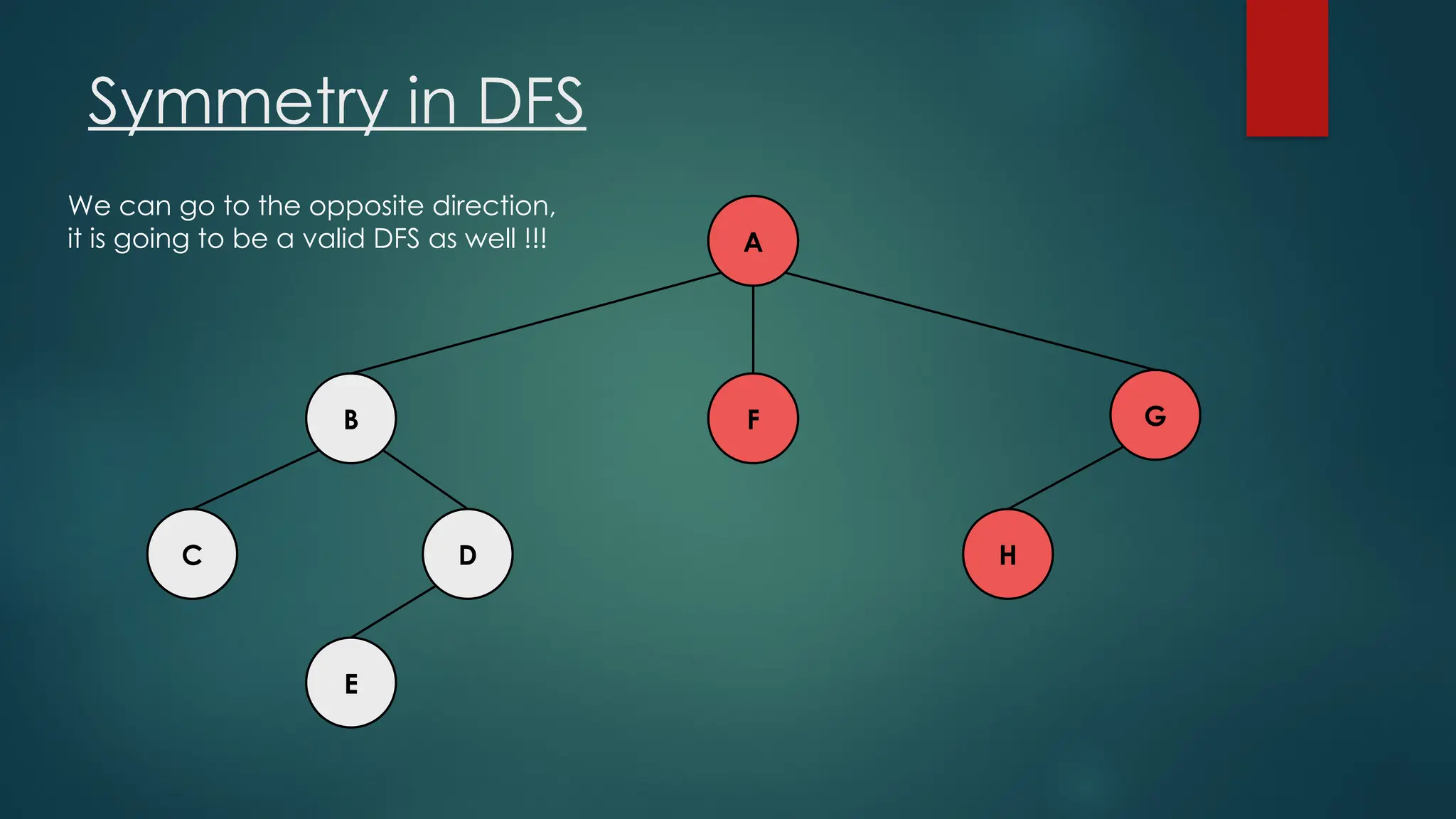
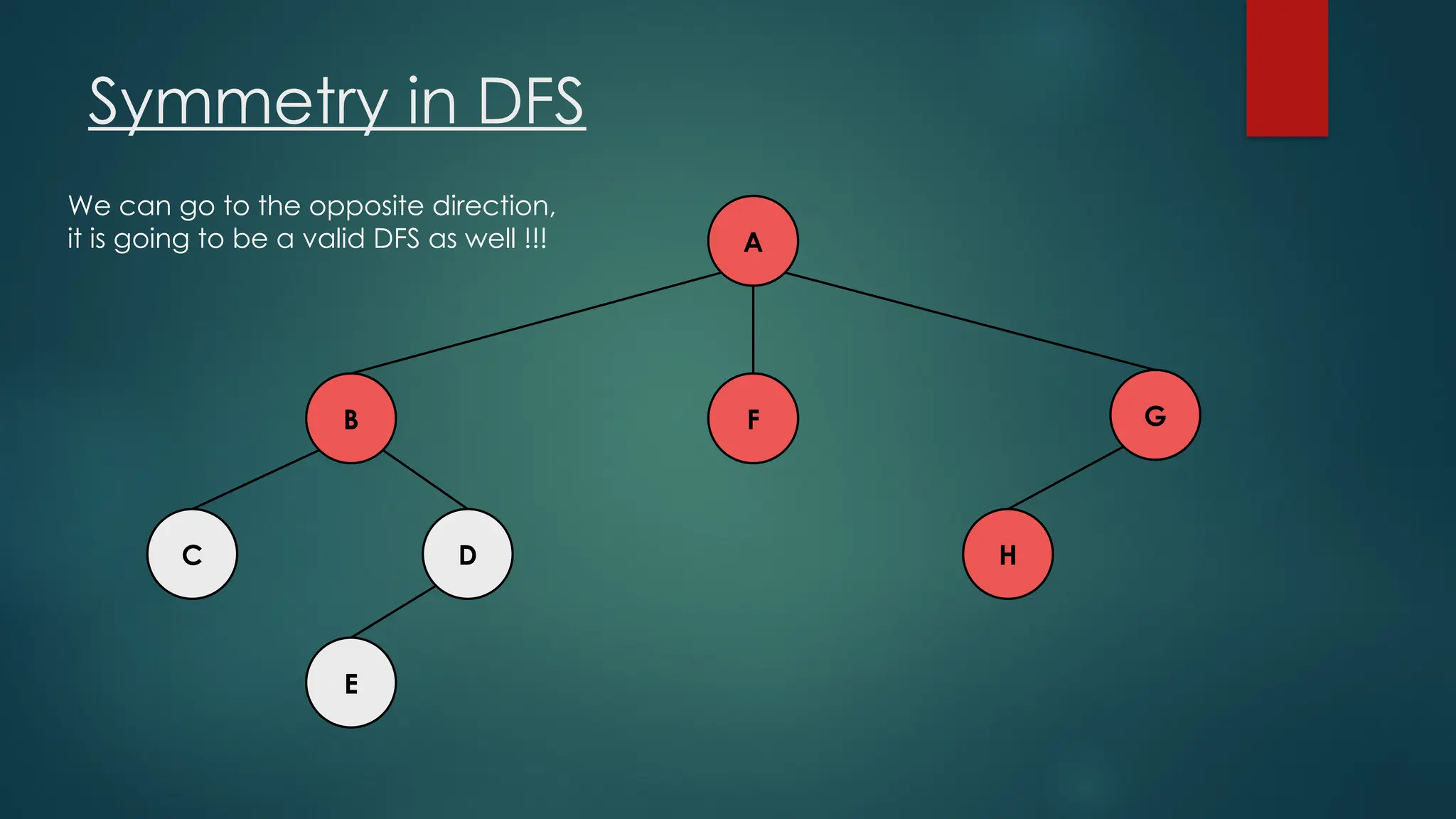
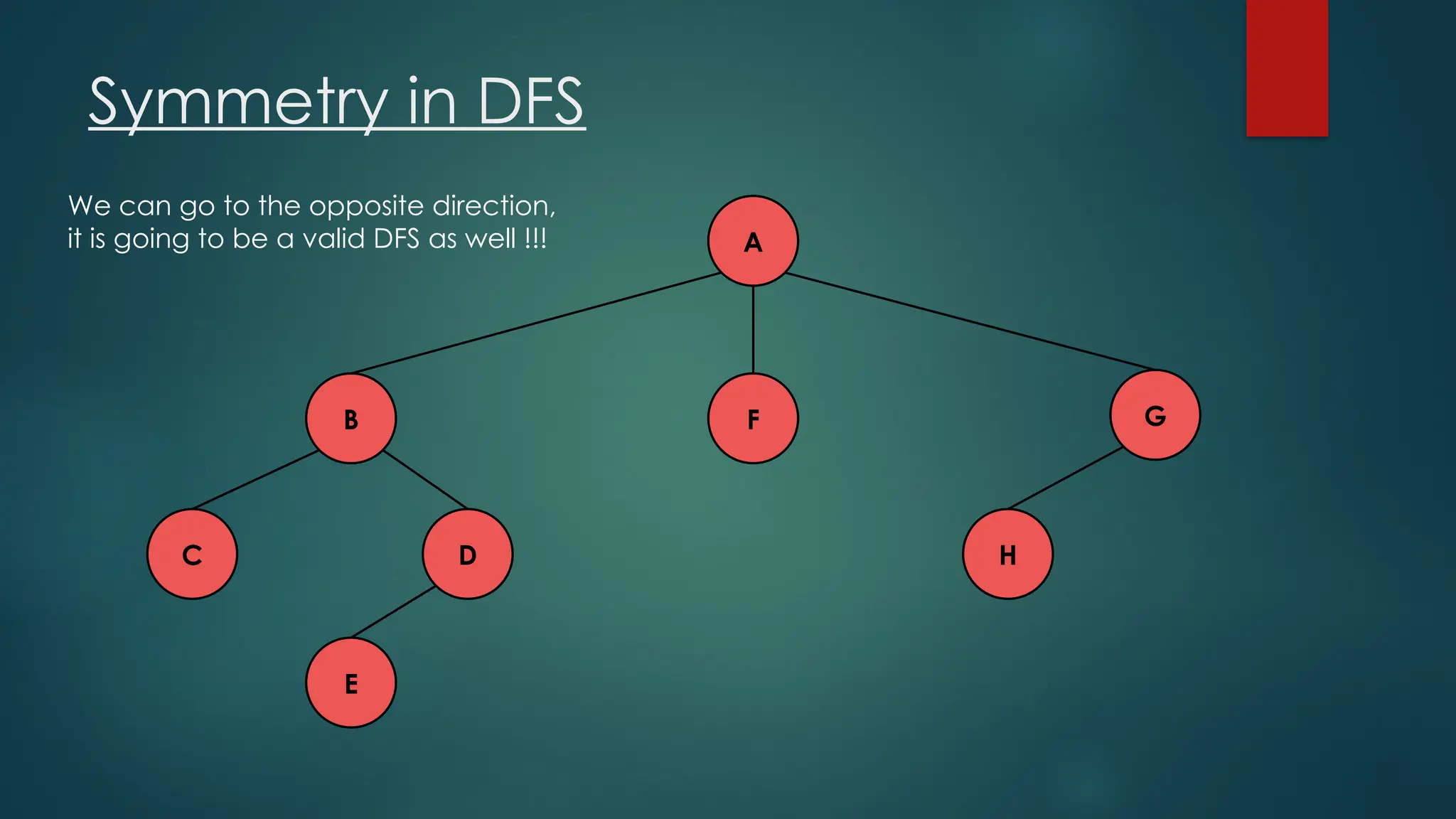
The document discusses breadth-first search (BFS) and depth-first search (DFS) algorithms for graph traversal, detailing their advantages, applications, and implementations. BFS visits every vertex once and has a time complexity of O(V + E) but uses more memory, while DFS explores branches as far as possible with slightly better memory efficiency. Applications include artificial intelligence, garbage collection, topological ordering, and cycle detection.

1. BREADTH FIRST
SEARCH
BFS

2. Breadth-first search
 What is it good for?
 We have a graph and we want to visit every node  we can do it with
BFS
 We visit every vertex exactly once
 We visit the neighbours then the neighbours of these new vertices and
so on
 Running time complexity: O(V+E)
 Memory complexity is not good: we have to store lots of references
 Thats why DFS is usually preferred
 BUT it constructs a shortest path: Dijkstra algorithm does a BFS if all the
edge weights are equal to 1

3. Breadth-first search
bfs(vertex)
Queue queue
vertex set visited true
queue.enqueue(vertex)
while queue not empty
actual = queue.dequeue()
for v in actual neighbours
if v is not visited
v set visited true
queue.enqueue(v)
ITERATION
We have an empty queue at the beginning
and we keep checking whether we have visited
the given node or not
~ keep iterating until queue is not empty

4. A
C H
D
E
F G
B
Queue: { }

5. A
C H
D
E
F G
B
Queue: { A }

6. A
C H
D
E
F G
B
Queue: { A } dequeue node A to be able to process its

7. A
C H
D
E
F G
B
Queue: { } dequeue node A to be able to process its neighbours  visit all the children, if a node is
unvisited then enqueue it !!!

8. A
C H
D
E
F G
B
Queue: { B } node B is not visited  put it to the queue

9. A
C H
D
E
F G
B
Queue: { F B } node F is not visited  put it to the queue

10. A
C H
D
E
F G
B
Queue: { G F B } node G is not visited  put it to the queue

11. A
C H
D
E
F G
B
Queue: { G F B } dequeue the next node  it is B and visit its children + put them into the queue
if necessary

12. A
C H
D
E
F G
B
Queue: { G F } dequeue the next node  it is G and visit its children + put them into the queue
if necessary

13. A
C H
D
E
F G
B
Queue: { C G F } dequeue the next node  it is G and visit its children + put them into the queue
if necessary

14. A
C H
D
E
F G
B
Queue: { D C G F } dequeue the next node  it is G and visit its children + put them into the queue
if necessary

15. A
C H
D
E
F G
B
Queue: { D C G F }

16. A
C H
D
E
F G
B
Queue: { D C G }

17. A
C H
D
E
F G
B
Queue: { D C G }

18. A
C H
D
E
F G
B
Queue: { D C }

19. A
C H
D
E
F G
B
Queue: { H D C }

20. A
C H
D
E
F G
B
Queue: { H D C }

21. A
C H
D
E
F G
B
Queue: { H D }

22. A
C H
D
E
F G
B
Queue: { H D }

23. A
C H
D
E
F G
B
Queue: { H }

24. A
C H
D
E
F G
B
Queue: { E H }

25. A
C H
D
E
F G
B
Queue: { E H }

26. A
C H
D
E
F G
B
Queue: { E }

27. A
C H
D
E
F G
B
Queue: { E }

28. A
C H
D
E
F G
B
Queue: { } the queue is empty  FINISHED !!!

29. A
C H
D
E
F G
B
Summary

30. A
C H
D
E
F G
B
Summary

31. A
C H
D
E
F G
B
Summary

32. A
C H
D
E
F G
B
Summary

33. A
C H
D
E
F G
B
Summary

34. Applications
 In artificial intelligence / machine learning it can prove to be very
important: robots can discover the surrounding more easily with BFS
than DFS
 It is also very important in maximum flow: Edmonds-Karp algorithm
uses BFS for finding augmenting paths
 Cheyen’s algorithm in garbage collection  it help to maintain
active references on the heap memory
 It uses BFS to detect all the references on the heap
 Serialization / deserialization of a tree like structure ( for example
when order does matter )  it allows the tree to be reconstructed in
an efficient manner !!!

35. DEPTH FIRST
SEARCH
DFS

36. Depth-first search
 Depth-first search is a widely used graph traversal algorithm besides
breadth-first search
 It was investigated as strategy for solving mazes by Trémaux in the
19th century
 It explores as far as possible along each branch before
backtracking // BFS was a layer-by-layer algorithm
 Time complexity of traversing a graph with DFS: O(V+E)
 Memory complexity: a bit better than that of BFS !!!

37. Depth-first search
dfs(vertex)
vertex set visited true
print vertex
for v in vertex neighbours
if v is not visited
dfs(v)
RECURSION
dfs(vertex)
Stack stack
vertex set visited true
stack.push(vertex)
while stack not empty
actual = stack.pop()
for v in actual neighbours
if v is not visited
v set visited true
stack.push(v)
ITERATION

38. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

39. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

40. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

41. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

42. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

43. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

44. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

45. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

46. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

47. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

48. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

49. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

50. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

51. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

52. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

53. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

54. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

55. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

56. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

57. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!

58. A
C H
D
E
F G
B
Recursively check every
unmarked vertices!
FINISHED
There is no unvisited vertices for the starting
vertex  it means we are done

59. Applications
 Topological ordering
 Kosaraju algorithm for finding strongly connected components in a
graph which can be proved to be very important in
recommendation systems ( youtube )
 Detecting cycles ( checking whether a graph is a DAG or not )
 Generating mazes OR finding way out of a maze

60. Revisiting breadth-first search
A
C H
D
E
F G
B

61. Revisiting breadth-first search
A
C H
D
E
F G
B

62. Revisiting breadth-first search
A
C H
D
E
F G
B

63. Revisiting breadth-first search
A
C H
D
E
F G
B

64. Revisiting breadth-first search
A
C H
D
E
F G
B

65. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

66. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

67. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

68. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

69. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

70. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

71. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

72. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!

73. Symmetry in DFS
A
C H
D
E
F G
B
We can go to the opposite direction,
it is going to be a valid DFS as well !!!