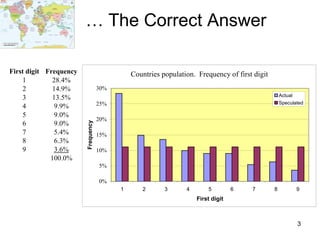
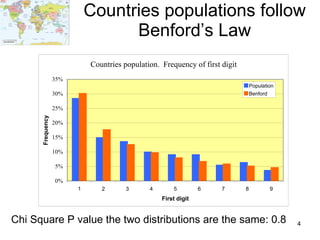
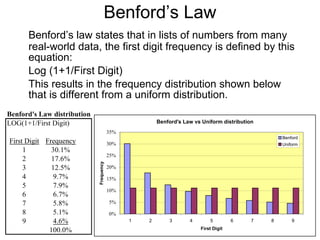
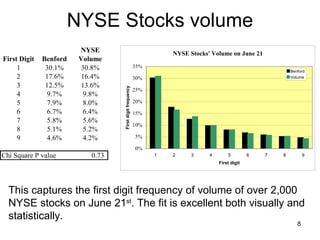
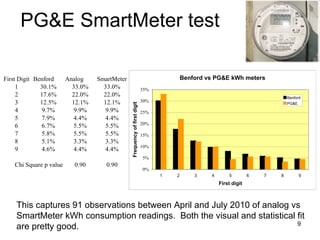
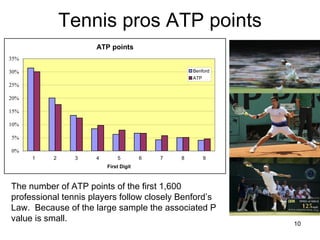
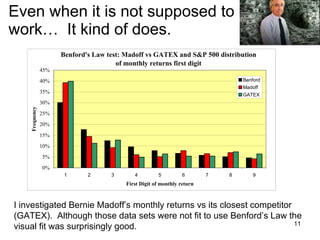
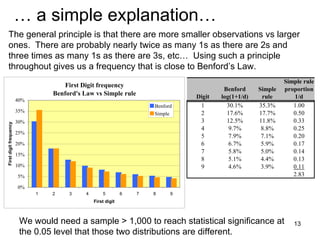
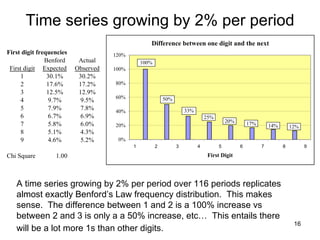
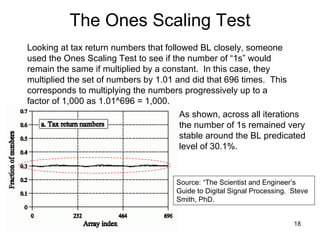
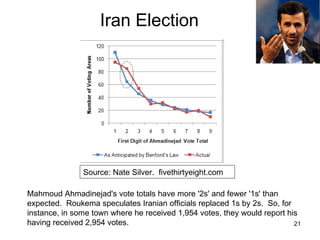
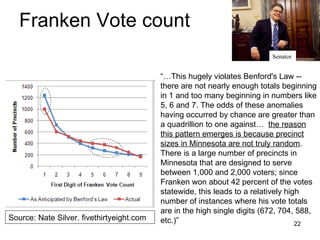
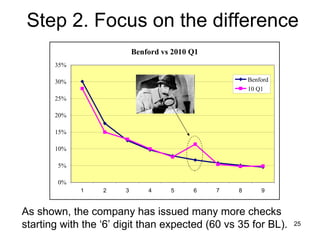
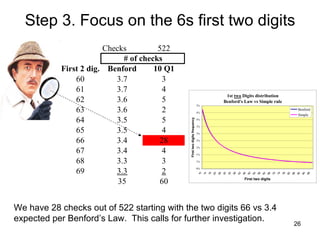
Benford's law states that in many real-world data sets, the distribution of first digits is not uniform, but rather follows a specific logarithmic pattern. This document discusses how Benford's law can be applied to detect anomalies and potential fraud in data sets involving areas like political elections, tax returns, insurance claims, and financial records. Specific examples are given showing how analyzing deviations from Benford's law helped uncover cases of electoral fraud, accounting fraud, and check fraud involving millions of dollars. The key is that Benford's law helps identify unexpected patterns within data that are worth further investigation for potential fraudulent activities.

1. Benford’s Law… Is it magic? Gaetan “Guy” Lion July 2010

3. … The Correct Answer

4. Countries populations follow Benford’s Law Chi Square P value the two distributions are the same: 0.8

6. When does this law work? The data crosses at least one scale (or order of magnitude) as shown below: You preferably need a sample > 100.

7. Demographic data follows Benford Law very closely The U.S. has over 3,000 counties. All shown demographic measures follow Benford’s Law pretty closely. This very large sample renders the Chi Square Goodness of fit test very (if not excessively) rigorous.

8. NYSE Stocks volume This captures the first digit frequency of volume of over 2,000 NYSE stocks on June 21 st . The fit is excellent both visually and statistically.

9. PG&E SmartMeter test This captures 91 observations between April and July 2010 of analog vs SmartMeter kWh consumption readings. Both the visual and statistical fit are pretty good.

10. Tennis pros ATP points The number of ATP points of the first 1,600 professional tennis players follow closely Benford’s Law. Because of the large sample the associated P value is small.

11. Even when it is not supposed to work… It kind of does. I investigated Bernie Madoff’s monthly returns vs its closest competitor (GATEX). Although those data sets were not fit to use Benford’s Law the visual fit was surprisingly good.

12. Is Benford Law magic? Bacteria > No, a simple rule is that there are more small things than large things in the universe…

13. … a simple explanation… The general principle is that there are more smaller observations vs larger ones. There are probably nearly twice as many 1s as there are 2s and three times as many 1s as there are 3s, etc… Using such a principle throughout gives us a frequency that is close to Benford’s Law. We would need a sample > 1,000 to reach statistical significance at the 0.05 level that those two distributions are different.

15. Benford vs Simple rule for first two digits When dealing with first two digits (10 – 99), Benford’s Law and the Simple Rule have indistinguishable distributions. You would need samples > 700,000 to reach statistical significance at the 0.05 level that the two distributions are different.

16. Time series growing by 2% per period A time series growing by 2% per period over 116 periods replicates almost exactly Benford’s Law frequency distribution. This makes sense. The difference between 1 and 2 is a 100% increase vs between 2 and 3 is only a a 50% increase, etc… This entails there will be a lot more 1s than other digits.

18. The Ones Scaling Test Looking at tax return numbers that followed BL closely, someone used the Ones Scaling Test to see if the number of “1s” would remain the same if multiplied by a constant. In this case, they multiplied the set of numbers by 1.01 and did that 696 times. This corresponds to multiplying the numbers progressively up to a factor of 1,000 as 1.01^696 = 1,000. As shown, across all iterations the number of 1s remained very stable around the BL predicated level of 30.1%. Source: “The Scientist and Engineer’s Guide to Digital Signal Processing. Steve Smith, PhD.

21. Iran Election Mahmoud Ahmadinejad's vote totals have more '2s' and fewer '1s' than expected. Roukema speculates Iranian officials replaced 1s by 2s. So, for instance, in some town where he received 1,954 votes, they would report his having received 2,954 votes. Source: Nate Silver. fivethirtyeight.com

22. Franken Vote count “…This hugely violates Benford's Law -- there are not nearly enough totals beginning in 1 and too many beginning in numbers like 5, 6 and 7. The odds of these anomalies having occurred by chance are greater than a quadrillion to one against… the reason this pattern emerges is because precinct sizes in Minnesota are not truly random . There is a large number of precincts in Minnesota that are designed to serve between 1,000 and 2,000 voters; since Franken won about 42 percent of the votes statewide, this leads to a relatively high number of instances where his vote totals are in the high single digits (672, 704, 588, etc.)” Source: Nate Silver. fivethirtyeight.com Senator

23. Inspector Clouseau demonstrates how to run a fraud investigation

24. Detecting fraud (an example). Step 1 A company issued 483 checks in 2009 Q4 that was audited and everything checked out. It also issued 522 checks in 2010 Q1. A fraud investigator notes that 09 Q4 pattern fit Benford Law very closely (P value 0.84). He notes that the fit deteriorated in 010 Q1 9 (P value 0.06).

25. Step 2. Focus on the difference As shown, the company has issued many more checks starting with the ‘6’ digit than expected (60 vs 35 for BL).

26. Step 3. Focus on the 6s first two digits We have 28 checks out of 522 starting with the two digits 66 vs 3.4 expected per Benford’s Law. This calls for further investigation.

27. Step 4. Focus on the 66s to three digits Carrying this analysis to the first three digits, we see an unusual # of checks starting with ‘666’ and ‘668.’ Later, we find that the checks starting with ‘666’ were legitimate ones that four employees wrote to pay for a monthly service that cost $5.95 per month plus tax or $6.66 with tax. Meanwhile, 9 of the 10 checks starting with ‘668’ were fraudulent ones.