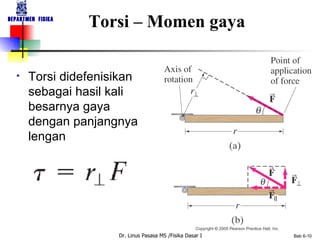
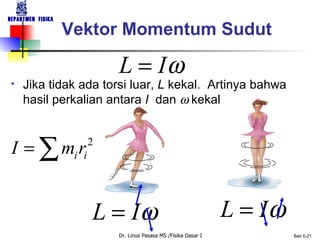
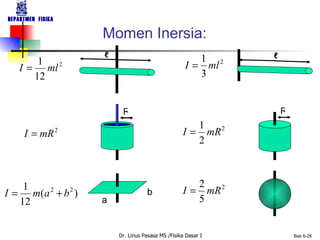
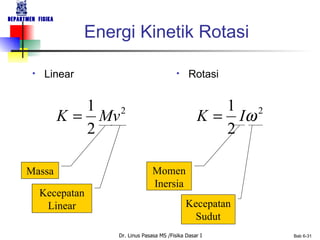
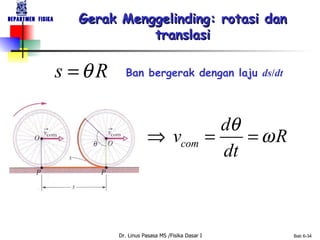
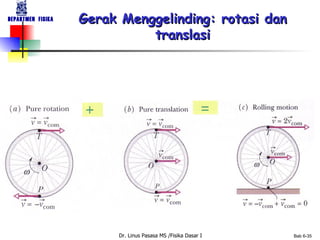
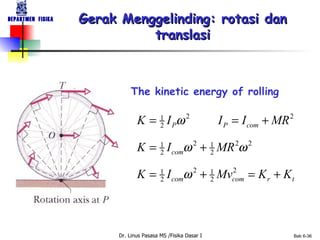
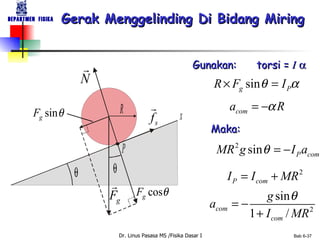
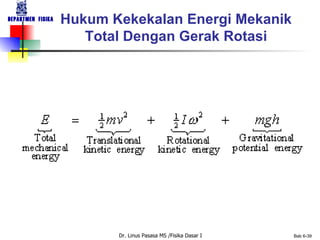
Dokumen tersebut membahas tentang konsep-konsep dasar gerak rotasi dan besaran-besaran vektor yang terkait dengan gerak rotasi seperti kecepatan sudut, percepatan sudut, momentum sudut, dan momen inersia. Dokumen tersebut juga membahas hukum-hukum dasar mekanika gerak rotasi seperti hukum kekekalan momentum sudut dan analoginya dengan hukum kekekalan momentum linear untuk gerak translasi.

1. BENDA TEGAR

5. Gerak Rotasi & Pergeseran Sudut Arah kecepatan sudut: Aturan tangan kanan

7. Persamaan Kinematika Rotasi

22. Momen Inersia Momen Inersia bagi suatu sistem partikel benda tegar didefenisikan sebagai I = momen inersia benda tegar, menyatakan ukuran inersial sistem untuk berotasi terhadap sumbu putarnya

23. Momen Inersia Untuk benda yang mempunyai distribusi massa kontinu, momen inersianya diberikan dalam bentuk integral Dimana Elemen Volume dm x y z

26. Momen Inersia Hasilnya adalah Massa dari lempengan tersebut Momen Inersia benda

27. Dalil Sumbu Sejajar Untuk benda tegar bermassa M yang berotasi terhadap sumbu putar sembarang yang berjarak h dari sumbu sejajar yang melalui titik pusat massanya ( I CM diketahui), momen inersia benda dapat ditentukan dengan menggunakan: Dalil Sumbu Sejajar

28. Momen Inersia: ℓ R R ℓ a b

34. Gerak Menggelinding: rotasi dan translasi Ban bergerak dengan laju ds / dt

35. Gerak Menggelinding: rotasi dan translasi

36. Gerak Menggelinding: rotasi dan translasi The kinetic energy of rolling

37. Gerak Menggelinding Di Bidang Miring Gunakan: torsi = I  Maka:

39. Hukum Kekekalan Energi Mekanik Total Dengan Gerak Rotasi

42. Hubungan Besaran Gerak Linear - Rotasi Kerja energi kinetik Hk. Newton’s gaya massa percepatan kecepatan perpindahan angular linear