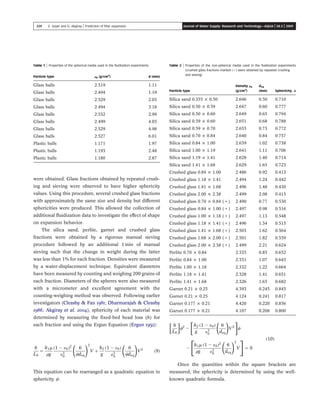
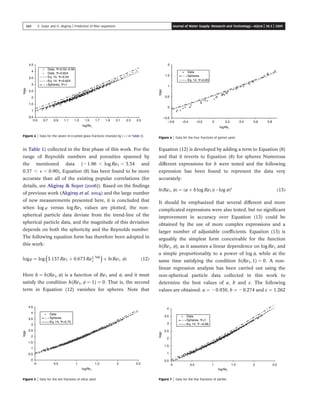
This document presents a new equation to predict the expansion of granular filter media during backwashing that accounts for particle shape. The equation was developed using fluidization experiments with various spherical and non-spherical materials, including glass spheres, plastic spheres, silica sand, garnet sand, perlite, and crushed glass. Existing equations were found to not fully capture the influence of particle shape, particularly at different Reynolds numbers. The proposed new equation provides an improved fit to experimental data for both spherical and non-spherical particles over a range of Reynolds numbers.