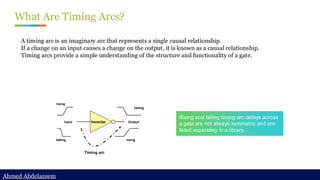
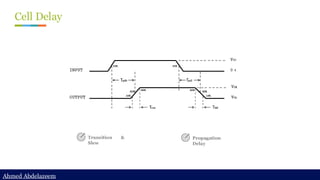
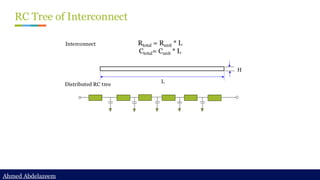
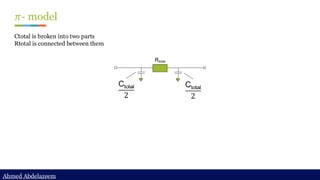
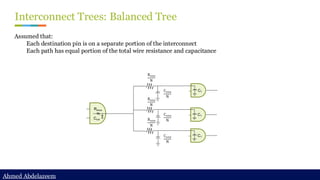
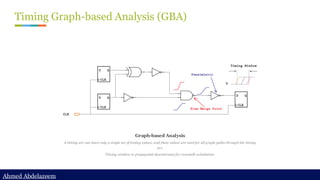
Static timing analysis (STA) is a method of validating the timing performance of a design by checking all possible paths for timing violations. STA breaks a design down into timing paths, calculates the signal propagation delay along each path, and checks for violations of timing constraints inside the design and at the input/output interface.

1. Ahmed Abdelazeem
Ahmed Abdelazeem
Ahmed Abdelazeem
Ahmed Abdelazeem
STA Basic Concepts
{ Concepts } + { Technique }
Ahmed Abdelazeem

2. Ahmed Abdelazeem
Ahmed Abdelazeem
02 Delay Calculation
✓ Timing Graph/Arcs/Sense/Path
✓ Cell Delay Model
✓ Wire Delay Model
✓ RC tree delay algorithm
✓ Analysis Mode
✓ GBA & PBA
✓ Parasitic Scaling & Timing Derating

3. Ahmed Abdelazeem
Ahmed Abdelazeem
Path Delay: Basic Approach
Flop
2
0
1
4
1
0
3
1
Path delay = 2 + 1 + 1 + 3 + 0 + 4 + 1 + 4 + 0 = 16 time units
clock
Cell timing arc Net timing arc
path
4
This illustration shows the calculation of the path delays.
Simple Design Showing Timing Arcs and Timing Paths

4. Ahmed Abdelazeem
Ahmed Abdelazeem
Delay Dependencies
trise
CL
td
td ~ CL
td ~ trise
td
CL
trise
trise 10ps – 120ps
Cload 10fF – 50 fF
td ~ Process Variations
td ~ Voltage
td ~ Temperature
Process: TT, FF, SS, etc.
Voltage: ∓10%
Temperature: -40 -1250
C
P:SS
V:0.9
T:-40

5. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Graph
Schematic
The logic connectivity has been established after netlist is read in and design
linked.
Timing Graph
Represent the design as a node graph. The ports and pins in the design become
the nodes in the graph, and the timing arcs become the connections between the
nodes

6. Ahmed Abdelazeem
Ahmed Abdelazeem
What Are Timing Arcs?
Rising and falling timing arc delays across
a gate are not always symmetric and are
listed separately in a library.
Input Output
falling
rising
falling
rising
Timing arc
Inverter
A timing arc is an imaginary arc that represents a single causal relationship.
If a change on an input causes a change on the output, it is known as a causal relationship.
Timing arcs provide a simple understanding of the structure and functionality of a gate.

7. Ahmed Abdelazeem
Ahmed Abdelazeem
Sequential cell
Sequential cell have timing arcs from the clock to outputs and
timing constraints for data pins w.r.t. the clock.
This is because a change in the output can only be caused by a change
at the clock pin for a simple flop.
Combinational Gate
Combinational logic cells have timing arcs from each input to each
output.
Timing Arcs

8. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Arcs: Cell and Net Delay
Each stage delay (Cell delay + Net delay) represents the time
required to propagate a signal from the input of one gate to the
input of the next.
Cell Delay
Transistors within a cell take a certain amount of time to
switch. Therefore, a change to the input of a cell takes time
to cause a change to the output.
Net Delay
Net delay is the delay between the time a signal is first
applied to a net and the time it takes to reach other devices
connected to that net.
Delays encountered in digital circuitry are composed of two
main components: cell delay and net delay.
A Y
VDD
VSS
Transistor
Representation
A Y
Cell
delay
Net delay
(Interconnect)
A A Y

9. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Group Names
N Parameter Unit Symbol Figure Definition
1. Rise transition
time
rise_transition
ns tR The time it takes a driving pin to
make a transition from kVDD to (1-
k)VDD value. Usually k=0.1 (also
possible k=0.2, 0.3, etc)
2. Fall transition time
fall_transition
ns tF
The time it takes a driving pin to
make a transition from (1-k)VDD to
kVDD value. Usually k=0.1 (also
possible k=0.2, 0.3, etc)
3. Propagation delay
low-to-high (rise)
cell_rise
ns tPLH
(tPR)
Time difference between the input
signal crossing a 0.5VDD and the
output signal crossing its 0.5VDD
when the output signal is changing
from low to high
4. Propagation delay
high-to-low (Fall)
cell_fall
ns tPHL
(tPF)
Time difference between the input
signal crossing a 0.5VDD and the
output signal crossing its 0.5VDD
when the output signal is changing
from high to low
VSS
0.1VDD
0.9VDD
tR
VDD
VSS
0.1VDD
0.9VDD
tF
VDD
tPLH
0.5VDD
0.5VDD
IN
OUT
tPHL
0.5VDD
0.5VDD
IN
OUT

10. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Constraints: Timing Types
N Parameter Unit Symbol Figure Definition
1 Setup time
(only for flip-flops or latches)
ns tSU The minimum period in which the input
data to a flip-flop or a latch must be
stable before the active edge of the clock
occurs
2
.
.
Hold time
(only for flip-flops or latches)
ns tH The minimum period in which the input
data to a flip-flop or a latch must remain
stable after the active edge of the clock
has occurred
3 Removal time
(only for asynchronous Set or
Reset)
ns tREM The minimum time in which the
asynchronous Set or Reset pin to a flip-
flop or latch must remain enabled after
the active edge of the clock has occurred
4 Recovery time
(only for asynchronous Set or
Reset)
ns tREC The minimum time in which Set or Reset
must be held stable after being
deasserted before next active edge of the
clock occurs
0.5VDD
0.5VDD
DATA
CLOCK tH
0.5VDD
0.5VDD
DATA
CLOCK
tSU
SET (RESET)
CLOCK
tREM
0.5VDD
0.5VDD
0.5VDD
SET (RESET)
CLOCK
tREC
0.5VDD
Setup/Hold, Recovery/Removal Constraints
removal_rising,
removal_falling
setup_rising
setup_falling
hold_rising
hold_falling
recovery_rising,
recovery_falling

11. Ahmed Abdelazeem
Ahmed Abdelazeem
Non-unate Arc (state-dependent)
Output transition cannot be determined solely from the direction
of change of an input but also depends upon the state of the other
inputs. E.g. XOR gate
Positive Unate Arc
A rising transition on an input causes the output to rise or not change.
A falling transition on an input causes the output to fall or not change.
E.g. AND/OR gate
Timing Sense (unateness)
Negative Unate Arc
A rising transition on an input causes the output to fall or not change.
A falling transition on an input causes the output to rise or not
change.
E.g. NAND/NOR gate

12. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Path: valid/leakage/don’t care?
Valid Path
Real functional path
Leakage Path
False path due to nature of STA
Don’t Care Path
Static path or unintended path

13. Ahmed Abdelazeem
Ahmed Abdelazeem
Late and Early Path
Max Timing Path (Long Path / Late Path)
The path with the largest delay between two end points. -> for setup
check
Min Timing Path (Short Path / Early Path)
The path with the smallest delay between two end points. -> for hold
check

14. Ahmed Abdelazeem
Ahmed Abdelazeem
Drive Strength
Slower, Smaller footprint, Higher Resistance
Less current and slower slew rate, but consume lower power
Faster, Larger footprint, Lower Resistance
Draw more current thus faster slew rate, but consume more power
Drive Strength
The inverse of pull-up/pull-down resistance. In general the cells are designed to have similar drive strength for pull-up/pull-down structures.
When the CMOS cell switches state, the speed of switching is governed by how fast the capacitance on the output net can be charged/discharged.
Thus the path resistance are a major factor in determining the speed of CMOS cell.

15. Ahmed Abdelazeem
Ahmed Abdelazeem
Cell Delay
Propagation
Delay
Transition &
Slew

16. Ahmed Abdelazeem
Ahmed Abdelazeem
Cell Delay Model
Approximation to Real Physics
Trade-off between Accuracy and Speed

17. Ahmed Abdelazeem
Ahmed Abdelazeem
Linear Delay Model
1
• Slope Delay (Tslope)
- The transition time of the previous gate
• Intrinsic Delay (Tintrinsic)
- Delay of an element
• Transition time (Ttransition)
- Delay introduced by capacitive load on driving pin
- Ttransition = Rdrive ∗ σpins Cpin + Cwire
• Connect Delay (Tconnect)
- Delay from transition of the driving pin to
endpoint changing after the
T𝑡𝑜𝑡𝑎𝑙 = T𝑠𝑙𝑜𝑝𝑒 + T𝑖𝑛𝑡𝑟𝑖𝑛𝑠𝑖𝑐 + T𝑡𝑟𝑎𝑛𝑠𝑖𝑡𝑖𝑜𝑛 + T𝑐𝑜𝑛𝑛𝑒𝑐𝑡
Ttransition
B
A
D
C
Tconnect
Tslope Tintrinsic

18. Ahmed Abdelazeem
Ahmed Abdelazeem
Non-Linear Delay Model
2
Ttransition
B
A
D
C
Tconnect
Tslope Tintrinsic
Transition time (Ttransition)
Delay introduced by capacitive load on driving pin (measured, not calculated)
Propagation delay (Tpropagation)
Time from the 50 percent input pin voltage until the gate output just begins to switch (10 percent output voltage)
(measured, not calculated)
Connect Delay (Tconnect)
Delay from transition of the driving pin (estimated interconnect delay)
Transition time and Propagation delay for each cell are measured beforehand and stored in form
of lookup table
Ttotal = Tpropagation + Ttransition + Tconnect

19. Ahmed Abdelazeem
Ahmed Abdelazeem
Nonlinear Delay Calculation Example
net n1
Ctotal
G1
G2
G3
P T
T
rise
fall fall
NLDM model is a voltage-based delay calculation model
which is widely used models representing the response
characteristics of cells in the libraries. It is very simple and
less time consuming for the tools to obtain the response of
the cells. This model uses two dimensional tables to
represent the cell delay, output slew and other timing
checks. In this method of modelling the driver cell is
modeled to be a voltage source with resistance in series
(Thevenin Model). The receiver is modeled to be a load
capacitor.
The NLDM table is in the form of a two-dimensional table.
Notice that the NLDM table is characterized under the
condition where the output wire resistance is zero since we
have no idea what the load will be when just creating the
library.

20. Ahmed Abdelazeem
Ahmed Abdelazeem
NLDM
2 NLDM (non-linear delay model, LUT)
* An important assumption is: Only one input is switching at a time.
Multi-input simultaneous switching is too complex for STA engine.
C load: Single capacitance model depends only on rise/fall min/max arc
condition

21. Ahmed Abdelazeem
Ahmed Abdelazeem
NLDM
Fall
Propagation
Delay
Output
Capacitance
Input
Transition
Time
x
y
z
0.20
0.34
0.56
0.72
1.23
10.2 30.8 58.7 99.9
110.1
151.6
cell _rise or cell _fall
table
output cap
Input slew
0.7
0.5
0.2
0.1
.023 .047 .065 .078 .091
Linear Delay model:
Delay = Intrinsic Delay + Slope_factor * Load(Cap)
Delay/Power are measured as
function of input slew and output cap
Input slew
Output cap

22. Ahmed Abdelazeem
Ahmed Abdelazeem
NLDM - library

23. Ahmed Abdelazeem
Ahmed Abdelazeem
NLDM - interpolation
Step #1 – Solve for coefficients
Use the 4 pre-characterized library data to calculates coefficients A, B, C, D for this
particular timing arc. (substitute X, Y, Z into the plane equation Z = A+ B * X + C *
Y + D * X * Y)
0.067 = A + B*0.064 + C*0.5 + D*0.064*0.5
0.071 = A + B*0.064 + C*1.0 + D*0.064*1.0
0.082 = A + B*0.128 + C*0.5 + D*0.128*0.5
0.087 = A + B*0.128 + C*1.0 + D*0.128*1.0
Step #2 – Interpolate the cell delay
Use the solved coefficients and the plane equation to calculate cell delay with input
transition and output load.
Cell delay = A + B*0.09 + C*0.67 + D*0.09*0.67

24. Ahmed Abdelazeem
Ahmed Abdelazeem
NLDM (C effective)
Effective Capacitance
When wire resistance is not negligible anymore, effective capacitance has to be
used for calculating delay through the driving cell. Single capacitance model
depends only on rise/fall min/max arc condition.
Resistive Shielding
The output capacitance seen from the drive point is effectively less than the total
capacitance of the wire. Near-end capacitance will be charged quicker than far-end
capacitance because of wire resistance.

25. Ahmed Abdelazeem
Ahmed Abdelazeem
NLDM – path delay

26. Ahmed Abdelazeem
Ahmed Abdelazeem
Composite Current Source Model (CCS)
3 CCS (composite current source)
Network model
C1 C2
⚫ The driver model uses a time-varying current source.
⚫ The receiver model consists of 2 different capacitors.
The first one is used as load up to the input delay threshold. A second capacitance value is used when the input
waveform reaches the threshold value.
⚫ CCS models are frequently used in advanced technology nodes.

27. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS model
2 CCS (composite current source)
Cload: voltage-dependent also depends on input slew/output capacitance

28. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS model
2 CCS (composite current source)
Cload: voltage-dependent also depends on input slew/output capacitance

29. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS Driver Model (conventional)
* Above is driver model only

30. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS Driver Model (compact)
Modeling with Base Curves and re-construct
Modelling I-V curve which is smoother. Only 6 parameters needed to model one
transition process. Reconstruct the waveform using pre-characterized “base curve”
Conventional CCS
Current v.s. Time and Voltage v.s. Time, too many sample points

31. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS Driver Model (compact)
Base Curves Lookup Table
Template

32. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS Driver Model (compact)
Compact Driver Model
*Application variable rc_driver_model_mode -> advance means the tool is
using CCS model
Index 3: Six essential
data
initial current - 1.24e+01
peak current - 2.47e+01
peak voltage - 2.86e-01
peak time - 4.46e-02
left base curve ID - 799
right curve ID – 6920

33. Ahmed Abdelazeem
Ahmed Abdelazeem
CCS Receiver Model
Compact Load Model
- Improved accuracy for both delay and slew calculation
- Consider non-linear effect such as miller effect
*Application variable rc_receiver_model_mode -> advance means the tool is using
CCS model

34. Ahmed Abdelazeem
Ahmed Abdelazeem
Synopsys Liberty Format (.lib)
library (Digital_Std_Lib) {
technology (cmos);
delay_model : table_lookup;
cell(AND2) {
area : 2;
pin(A) {
direction : input;
}
pin(B) {
direction : input;
}
pin(Z) {
direction : output;
function : "A*B";
timing() {
related_pin : “A" ;
timing_type : "combinational" ;
cell_rise(…) {
index_1("0.016, 0.032, 0.064”);
index_2("2, 4");
values("1.0020, 1.1280, 3.547 “,
"1.0080, 1.1310, 3.847 “ );
}
}
} /* end of pin */
} /* end of cell */
} /* end of library*/
trise
0.016 0.032 0.064
CL
2 1.0020 1.1280 3.547
4 1.0080 1.1310 1.1310
td
CL
trise
Lookup table

35. Ahmed Abdelazeem
Ahmed Abdelazeem
Cell Timing Data
cell (INVX1) {
pin (Y) {
timing () {
related_pin : "A";
timing_type : "combinational";
timing_sense : "negative_unate";
cell_rise ("del_1_7_7") {
index_1("0.016, 0.032, 0.064, 0.128, 0.256, 0.512, 1.024");
index_2("0.1, 0.25, 0.5, 1, 2, 4, 8");
values("0.016861, 0.0179019, 0.0195185, 0.0229259, 0.029658, 0.043145, 0.07712",
"0.0239648, 0.0255491, 0.0279298, 0.0319930, 0.0387540, 0.0520896, 0.0790211",
"0.0342118, 0.0366966, 0.0402223, 0.0462823, 0.0558327, 0.0705154, 0.0967339",
"0.0491695, 0.0524727, 0.0576512, 0.0665647, 0.0810999, 0.1027237, 0.1342571",
"0.0721332, 0.0765389, 0.0836775, 0.0960890, 0.1171612, 0.1497265, 0.1957640",
"0.1111560, 0.1164417, 0.1252609, 0.1422002, 0.1712097, 0.2171862, 0.2847010",
"0.1841131, 0.1901881, 0.2010298, 0.2194395, 0.2555983, 0.3182710, 0.4139452");
}
library(){
lu_table_template ("del_1_7_7") {
variable_1 : "input_net_transition";
index_1("1, 2, 3, 4, 5, 6, 7");
variable_2 : "total_output_net_capacitance";
index_2("1, 2, 3, 4, 5, 6, 7");
}

36. Ahmed Abdelazeem
Ahmed Abdelazeem
Topic 7: State-Dependent Delay (conditional timing)
Here are the rules for conditional timing:
1. When statement is where to specify the condition. If the condition expression evaluates to true
value, the following timing values in that case are active. At the same time, the default case are
disabled.
2. If there is state cannot be determined in a condition and result the entire condition to be
undetermined state as well (X), the condition will still be evaluated to be true.
3. The timing engine will pick the worst active timing value for this particular timing arc.
4. To disable a particular conditional timing, we must force its condition to be known state false.
E.g.
1. There are three cases in parallel as shown on the left. When B is true, not true or don’t care (the
default)
2. If there is no case analysis set for input B, then all three cases will be active and taking into account
by timing engine. It will pick the worst case to use to calculation. Usually the worst case is the default
case.
3. If we set case analysis to make B constant at one value, then only one of the above two cases will be
picked and used during calculation. The default case is also disabled.

37. Ahmed Abdelazeem
Ahmed Abdelazeem
NET “Wire”
Net is a wire connecting pins of standard cells and blocks. It:
• Has only one driver
• Can drive a number of fanout cells or blocks
• Can travel on multiple metal layers of the chip
• Can be broken up into segments for equivalent electrical representation

38. Ahmed Abdelazeem
Ahmed Abdelazeem
Interconnect Parasitics
Interconnect resistance - resistance between the output pin of a cell
and the input pins of the fanout cells
Interconnect capacitance - is comprised of grounded and between
neighboring signal routes
Interconnect inductance - arises due to current loops; effect of
inductance can be ignored for low frequencies

39. Ahmed Abdelazeem
Ahmed Abdelazeem
Overview
Cells
Input capacitances
Net parasitics
I1
I2 O2
O1
I1
I2
O2
O1
I1
I2 O2
O1

40. Ahmed Abdelazeem
Ahmed Abdelazeem
RC Tree of Interconnect
Distributed RC tree
H
L
Interconnect Rtotal = Runit * L
Ctotal= Cunit * L

41. Ahmed Abdelazeem
Ahmed Abdelazeem
T - model
Rtotal is broken in two parts
Ctotal is connected between them
Ctotal

42. Ahmed Abdelazeem
Ahmed Abdelazeem
𝜋- model
Ctotal is broken into two parts
Rtotal is connected between them
Rtotal

43. Ahmed Abdelazeem
Ahmed Abdelazeem
N Section Representation
Breaking Rtotal and Ctotal into multiple sections increases accuracy
T model:
π model:
Rtotal
2 ∗ N
Rtotal
N
Rtotal
N
Rtotal
N
Rtotal
2 ∗ N
Ctotal
N
Ctotal
N
Ctotal
N
Ctotal
N
Ctotal
N
Rtotal
2 ∗ N
Rtotal
N
Rtotal
N
Rtotal
N
Rtotal
2 ∗ N
Ctotal
2 ∗ N
Ctotal
N
Ctotal
N
Ctotal
N
Ctotal
N
Ctotal
2 ∗ N

44. Ahmed Abdelazeem
Ahmed Abdelazeem
Elmore Delay
Elmore delays are used to calculate delay of RC trees, which
Have single input node
Do not have resistive loops
Have capacitances only coupled to ground

45. Ahmed Abdelazeem
Ahmed Abdelazeem
Elmore Delay
Elmore delay equation is:
For example,
1 2 i-1 i N

46. Ahmed Abdelazeem
Ahmed Abdelazeem
Wire Load: Parasitic Effects
Parasitics are inevitable
Not known without layout
Delay and area will be incorrect/optimistic without estimation of parasitics
td
CL
trise
b
a
c y
t2=f(t2d,t2c,c2)
C3
ttotal= f(t2a,t2b,t2c,C1,C2,C3)
t2a
t2b
t2c
b
a
c y
t2=f(t2d,t2c,c2)
C3
ttotal= f(t2a,t2b,t2c,C1,C2,C3)
t2a
t2b
t2c
Delay > 0
Area >0

47. Ahmed Abdelazeem
Ahmed Abdelazeem
Estimating Parasitic Devices
▪ All parasitics depend on interconnect length
Generalization
R = length ∙ Runit length
C = length ∙ Cunit length
Area = length ∙ Areaunit length
▪ The more the fanout (output connections) the larger
the length
Length components
▪ The larger the chip (the more gates it has) the more
the length
length = f (gate count, fanout)

48. Ahmed Abdelazeem
Ahmed Abdelazeem
Wire Delay Model
Estimation? Extraction?
Parasitic Value can be estimated or extracted depends on whether or not the actual wire has been
routed.

49. Ahmed Abdelazeem
Ahmed Abdelazeem
RC Tree
RC Tree Topology
Single input node
No resistive loops
All capacitance are grounded

50. Ahmed Abdelazeem
Ahmed Abdelazeem
Prelayout: Wire Delay Model v.s. Topographical
Topographical
Wire Load Model

51. Ahmed Abdelazeem
Ahmed Abdelazeem
Prelayout: Wire Load Model
wire_load (name) {
area : float ;
capacitance : float ;
resistance : float ;
slope : float ;
{fanout_length (fanout, length) ;
...
}
}
wire_load_selection (name) {
{wire_load_from_area (min_area1,max_area1,wire_load_name1);
...}
}
default_wire_load : name ;
default_wire_load_selection : name ;
default_wire_load_area : float ;
default_wire_load_capacitance : float ;
default_wire_load_resistance : float ;
default_wire_load_mode : top | segmented | enclosed ;

52. Ahmed Abdelazeem
Ahmed Abdelazeem
Library: Wire Load Example
wire_load (“8000”) {
capacitance : 0.024051;
resistance : 1.860000e-03;
area : 0.010000;
slope : 30.285426;
fanout_length("1", "8.2750360");
fanout_length("2", "18.4914880");
fanout_length("3", "29.3531220");
}
default_wire_load : "8000";
default_wire_load_selection : "predcaps";
wire_load_selection (predcaps) {
wire_load_from_area (0.000000,200.000000, “4000");
wire_load_from_area (200.000000,8000.000000, "8000");
wire_load_from_area (8000.000000,16000.000000, "16000");
}
}

53. Ahmed Abdelazeem
Ahmed Abdelazeem
Prelayout: Wire Load Model

54. Ahmed Abdelazeem
Ahmed Abdelazeem
Prelayout: Wire Load Model

55. Ahmed Abdelazeem
Ahmed Abdelazeem
Library: Wire Load Table
wire_load_table (name) {
fanout_length(fanout, length);
fanout_capacitance(fanout, capacitance);
fanout_resistance(fanout, resistance);
fanout_area(fanout, area);
...
}
• It is practical to set the default_wire_load_mode to enclosed or segmented instead of top.
• If the default_wire_load_mode is set to top, all nets in both the top design and subblocks use the wire load
model selected from the area of the top design.
• If the default_wire_load_mode is set to enclosed, the nets fully enclosed within a design use the wire load
model selected from the area of that subdesign.
• If the default_wire_load_mode is set to segmented, the nets partially enclosed within a design use the
wire load model selected from the area of that subdesign.

56. Ahmed Abdelazeem
Ahmed Abdelazeem
Prelayout: Wire Load Model
Best-case Tree Balanced Tree Worst-case Tree

57. Ahmed Abdelazeem
Ahmed Abdelazeem
Interconnect Trees: Best-case Tree
Assumed that:
Load pin is physically adjacent to the driver
None of the wire resistance is in the path to the destination pin
Wire capacitance and pin capacitances act as load on the driver pin
Rdrive
Cout
C1
C1
C1
Rwire
Cwire

58. Ahmed Abdelazeem
Ahmed Abdelazeem
Interconnect Trees: Balanced Tree
Assumed that:
Each destination pin is on a separate portion of the interconnect
Each path has equal portion of the total wire resistance and capacitance
Rdrive
Cout
C1
C1
C1

59. Ahmed Abdelazeem
Ahmed Abdelazeem
Interconnect Trees: Worst-case Tree
Assumed that:
All the destination pins are together at the far end of the wire
Each destination pin sees the total wire resistance and the total wire capacitance
Rwire
Cwire
Rdrive
Cout C1
C1
C1
Rwire
Cwire

60. Ahmed Abdelazeem
Ahmed Abdelazeem
Post-layout: Parasitic & SPEF

61. Ahmed Abdelazeem
Ahmed Abdelazeem
Topic 8: Parasitic Annotation Issue
Common Reason for partial annotation
• Floating metal pieces
• Dangling pin/port in RTL
• Open nets
Consequences of annotation issue
• Tool could assume unrealistic delay value and create false violation
• Timing results cannot be trusted on these problematic nets having annotation issue
• Other nets might as well be impacted so the accuracy of timing analysis degrades.
Floating Metal Piece
Tiny Open

62. Ahmed Abdelazeem
Ahmed Abdelazeem
Elmore Delay Calculation
Application of Elmore Delay calculation
• For pre-route database which don’t have parasitic extracted yet.
• When analysis time is a concern, want fast turn around time.
• Can switch to AWE calculation if need better accuracy and correlation
with post-route, but at cost of runtime

63. Ahmed Abdelazeem
Ahmed Abdelazeem
Arnoldi Delay Calculation
Application of Arnoldi Delay calculation
• For post-route database with parasitic fully extracted. Usually used in APR tool
• Better RC delay calculation accuracy at cost of runtime
• Used in case where driver resistance is much less than the impedance of net to ground. (In case where net resistance is small compared to
drive resistance, Elmore delay can provide enough accuracy.)

64. Ahmed Abdelazeem
Ahmed Abdelazeem
Topic 9: report_delay_calculation
Since it’s using WLM, we want to set some timing derate to safeguard the margin.
In this report, we are enlarge all the datapath cell delay by a factor of 1.35
The calculated fall cell delay is 0.0631, multiply it
by the derating factor 1.35 results in 0.085,
which matches the timing report

65. Ahmed Abdelazeem
Ahmed Abdelazeem
Slew Degradation
Slew Degradation
Slowdown of the slew rate due to resistance as it travels along the
wire

66. Ahmed Abdelazeem
Ahmed Abdelazeem
Topic 10: Zero Interconnect Mode (Design Compiler)
Zero Interconnect, No slew degradation
- All Resistance and capacitance are treated as zero, no slew degradation along the wire
- Driver resistance and receiver pin cap are still kept non-zero

67. Ahmed Abdelazeem
Ahmed Abdelazeem
Slew Merge
Max Path Delay Calculation
Worst slew must be chosen and propagated forward. Choose slowest
slew to propagate to downstream
Min Path Delay Calculation
Worst slew must be chosen and propagated forward. Choose fastest
slew to propagate to downstream

68. Ahmed Abdelazeem
Ahmed Abdelazeem
Max delay & Min delay
Max Delay Arc
“Max” stimuli is used for cell arc delay calculation
1) Maximum annotated lumped capacitive wire load are used. → max SPEF
2) Maximum pin capacitance or receiver model are used. → max library
3) Maximum slew propagation is performed at slew merge point. → max
slew rate
Min Delay Arc
“Min” stimuli is used for cell arc delay calculation
1) Minimum annotated lumped capacitive wire load are used. → min SPEF
2) Minimum pin capacitance or receiver model are used. → min library
3) Minimum slew propagation is performed at slew merge point. → min slew
rate

69. Ahmed Abdelazeem
Ahmed Abdelazeem
Analysis Mode
Single Mode
Same delay across entire design.
* Setup check :
> Launch path: slowest path through max-delay arc, single operation condition, no
derating
> Capture path: fastest path through max-delay arc, single operation condition, no
derating
* Hold Check:
> Launch path: fastest path through max-delay arc, single operation condition, no
derating
> Capture path: slowest path through max-delay arc, single operation condition, no
derating
Best Case & Worst Case (bc_wc)
Two extreme PVT corners: One corner for either of setup or check
* Setup check :
> Launch path: slowest path through max-delay arc, worst-case operation condition, late derating
> Capture path: fastest path through max-delay arc, worst-case operation condition, early derating
* Hold Check:
> Launch path: fastest path through min-delay arc, best-case operation condition, early derating
> Capture path: slowest path through min-delay arc, best-case operation condition, late derating

70. Ahmed Abdelazeem
Ahmed Abdelazeem
Single Analysis Mode
The single mode is essentially the max delay-only
mode.
Only the max corner library information is
used.
Only constraints related to -max (or
unspecified) are used.
Only a single delay calculation pass is made.
Only the slowest slews are propagated.
root
FF1
FF2
One library
One corner

71. Ahmed Abdelazeem
Ahmed Abdelazeem
Best-Case Worst-Case Analysis Mode
Using both BC and WC libraries together is one way to model off-chip variation of delays due to external
temperature and voltage variations.
Setup analysis uses Max delay information for both clock and data.
Hold analysis uses Min delay information for both clock and data.
When is BCWC used?
The BCWC mode has often been the default for early steps of the implementation flow: preCTS, preRoute. Lately, OCV is
appearing earlier in the flow.
root
FF1
FF2
BC
library
Hold
(Min delays)
Setup
(Max delays)
Late path
Early path
Late path
Early path
WC
library
Launch clock
Capture clock

72. Ahmed Abdelazeem
Ahmed Abdelazeem
Analysis Mode (cont’d)
On-chip Variation (OCV)
The min/max delays and slews establish the ranges for possible delays and slews.
The actual delays and slews on the chip could be anywhere between these min/max bounds.
* Setup check :
> Launch path: slowest path through max-delay arc, worst-case operation condition, late derating
> Capture path: fastest path through min-delay arc, best-case operation condition, early derating
* Hold Check:
> Launch path: fastest path through min-delay arc, best-case operation condition, early derating
> Capture path: slowest path through max-delay arc, worst-case operation condition, late derating

73. Ahmed Abdelazeem
Ahmed Abdelazeem
What Are On-Chip Variations and Their Sources?
• Changes in physical parameters affect electrical
parameters, in turn causing delay variations.
- Variation in length, width, thickness.
- Doping variation.
OCV in STA:
Affects wire and cell delays.
Clock and data paths affected differently.
Increases pessimism in the design.
Location- and depth-based variations.
How to model on-chip variations!!!
Chip Variations are the intrinsic variability of
semiconductors subjected to process variations.
OCV, AOCV and POCV !!!

74. Ahmed Abdelazeem
Ahmed Abdelazeem
What Is Advanced OCV (AOCV)?
• Here, it shows the derate table for a buffer cell based
on the depth along the timing graph.
The shortcoming of OCV is that timing closure gets
difficult due to extra pessimism added with fixed
derates for the cells.
“Some stages will be faster, others slower. So the
more stages you have, the more it averages out.”
AOCV reduces the level of derating for each stage
on the basis that each successive stage will cancel
out the variation.
Depth 1 3 5 7 10 15 20 30
Late derate 1.6 1.4 1.3 1.25 1.21 1.17 1.12 1.1
Early derate 0.5 0.6 0.7 0.8 0.88 0.89 0.91 0.95
Clock branch
point
1 2
3
4
5
1 2
0
Data path
Clock path

75. Ahmed Abdelazeem
Ahmed Abdelazeem
What Is Parametric OCV (POCV)?
● POCV solves shortcomings of the AOCV approach:
●Inefficiency at ultralow voltage operation
(Voperation ~ Vthreshold)
●Cell timing dependency on slews and loads
● POCV analysis requires variation libraries in the form of
a Synopsys POCV library or as a Liberty Variation
Format (LVF) library.
● LVF includes arc-level absolute variations of cell delays,
output transitions, and timing checks as functions of
input slew and load.
POCV is a variation modeling technique that computes the impact of local process variations on the delay and
slew of each instance in the design at a given global variation corner. POCV propagates the sigma of arrival
and required times through the timing graph and then computes statistical characteristics of slack at all
timing pins.
PrimeTime
POCV

76. Ahmed Abdelazeem
Ahmed Abdelazeem
Liberty Variation Format (LVF)
cell (cell_name) {
ocv_derate_distance_group: ocv_derate_group_name;
...
pin | bus | bundle (name) {
direction: input | output;
timing() {
...
ocv_sigma_cell_rise(delay_lu_template_name){
sigma_type: early | late | early_and_late;
index_1 ("float, ..., float");
index_2 ("float, ..., float");
values ( "float, ..., float",
...,
"float, ..., float");
}
ocv_sigma_cell_fall(delay_lu_template_name){
sigma_type: early | late | early_and_late;
index_1 ("float, ..., float");
index_2 ("float, ..., float");
values ( "float, ..., float",
...,
"float, ..., float");
}
...
} /* end of timing */
...
} /* end of pin */
... (Statistical calculations happen during path tracing.)

77. Ahmed Abdelazeem
Ahmed Abdelazeem
Parametric OCV (POCV)
Parametric OCV uses a parameter as a delay sigma variation (not a derate factor):
A function of input slew and output load
Arc-level granularity
Accuracy and correlation with SPICE
(silicon)
Close correlation of GBA and PBA
(Statistical calculations happen during path tracing.)
Unique per-arc, per load/slew sigmas

78. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing (Arrival) Window
Timing Window
The timing window refers to the period of time between earliest
possible switching time and latest possible switching time.

79. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Graph-based Analysis (GBA)
● Here, it is assumed that for any input slew, the
output slew is 25% more than the input slew. If
slew at B is 500ps, then slew at Z is 625ps.
● In GBA, for calculating delay and slew propagation
through this AND gate, the worse input slew
(through B) is always considered, irrespective of
the fact that the path is through pin A or B.
● In the GBA mode, the PT considers both the worst
arrival and the worst slew in a path during timing
analysis, even if the worst slew corresponds to an
input pin different than the relevant pin for the
current path.
● This approach is used during the initial timing
analysis before the final signoff.
• This reduces the analysis runtime of the whole
design.
• But it gives a pessimistic result.
In static timing analysis (STA), Graph-Based Analysis is a pessimistic algorithm
for timing which is based on the worst slew propagation (slew merging). It is
the default mode of analysis in the implementation stage of the design.

80. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Graph-based Analysis (GBA)
Graph-based Analysis
A timing arc can have only a single set of timing values, and these values are used for all graph paths through the timing
arc.
Timing window is propagated downstream for crosstalk calculation.

81. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Path-based Analysis (PBA)
• GBA
• PBA
• Magnitude depicts the fast or slow slew.
• It considers path-based slews and actual
arrival times for both base and SI delay
calculations.
• It removes the pessimism that is introduced
due to slew merging at various nodes in the
design when the graph-based analysis is run.
• It is recommended to use during the final
stages of timing closure to ensure accuracy.
o This reduces the area, power dissipation,
and ECO cycles of your design but
imposes a huge runtime hit.
Path-Based Analysis (PBA) involves
re-timing the components of a timing path based
on the actual slew that is propagated in this path. a1
a5
a4
a3
a2
a6 a7
v1 v2
v3
v4
Q D
a1
a5
a4
a3
a2
a6 a7
v1 v2
v3
v4
Q D

82. Ahmed Abdelazeem
Ahmed Abdelazeem
Timing Path-based Analysis (PBA)
Path-based Analysis
The same timing arc can have different delay and slew for every path through the
arc.
Single edge is propagated downstream for crosstalk calculation.

83. Ahmed Abdelazeem
Ahmed Abdelazeem
Topic 11: report timing paths
Find the Difference from the two
Both are reporting the same timing path, not where goes differently?

84. Ahmed Abdelazeem
Ahmed Abdelazeem
Topic 11: report timing paths
report_timing -net -input -tran –cap –derate –voltage –crosstalk –max_paths –nworst
➢ -net not only shows the net between pin nodes, but also show the number of fanouts for each net
➢ -input shows the input pin through which the path is going through. It’s useful when tracing report through multiple input cells. Also, it split the delay associate to a cell into net
delay and cell delay.
➢ -tran shows both the input and output transition time used for or calculated by the delay calculation.
➢ -cap shows the total capacitance appear on the net, including both wire capacitance and input pin cap from next stage
➢ -derate show the derating factor used for the delay value.
➢ -voltage show the operating voltage set to do the analysis, useful when the design involves multiple power domain and rail voltage.
➢ -crosstalk show the delta delay calculated during signal integrity check or manually annotated.
➢ -max_path show the maximum total paths to be reported among all path groups. –nworst shows the maximum number of paths to be reported for a single endpoint
report_timing –pba_mode [none | path | exhaustive]
In addition to all the switches above, -pba_mode enables the pba mode reporting
➢ none (the default) - Path-based analysis is not applied.
➢ path - Path-based analysis is applied to paths after they have been gathered.
➢ exhaustive - An exhaustive path-based analysis path search algorithm is applied to
determine the worst path-based analysis path set in the design.
update_timing
If the timing constraints have been changed, STA engine will need to re-calculate the
timing graph again. Even though report_timing will re-time the design implicitly
(incrementally), It’s always a good practice to do an explicit update_timing explicitly
before report_timing.
By default, the update_timing command uses an efficient timing analysis algorithm that
requires minimal computation effort and updates existing timing analysis information
only where needed. You can override this default behavior using the -full option, which
causes the entire timing update to be performed from the beginning.

85. Ahmed Abdelazeem
Ahmed Abdelazeem
Chapter Summary
✓ Timing Graph/Arcs/Sense/Path
✓ Cell Delay Model
✓ Wire Delay Model
✓ RC tree delay algorithm
✓ Analysis Mode
✓ GBA & PBA
✓ Parasitic Scaling & Timing Derating

86. Ahmed Abdelazeem
Ahmed Abdelazeem
Ahmed Abdelazeem
Ahmed Abdelazeem
Thank You ☺