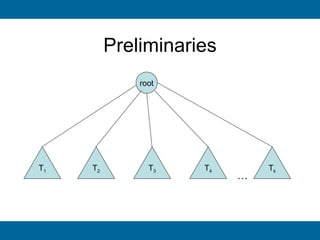
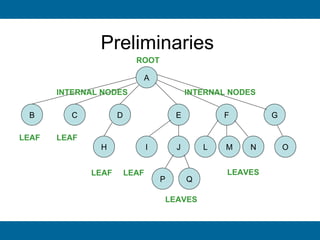
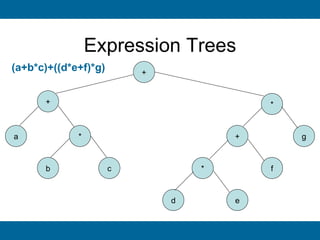
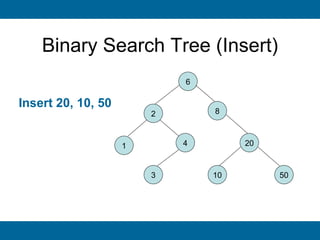
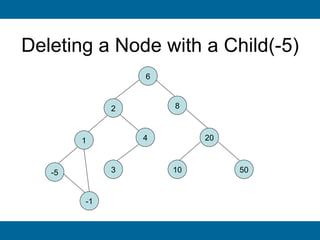
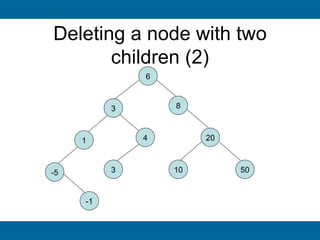
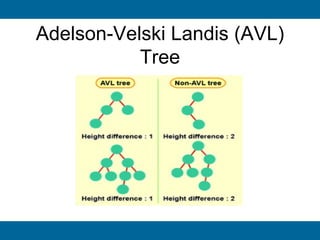
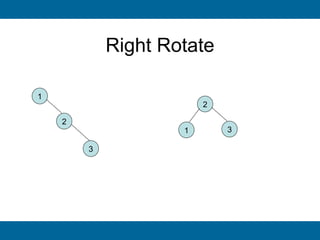
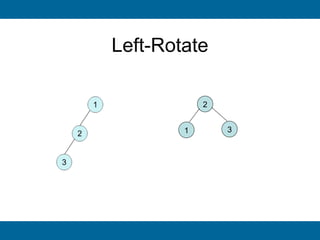
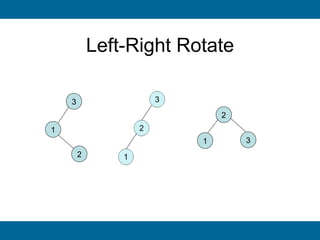
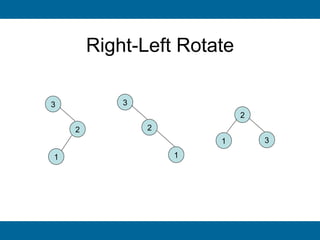
The document discusses binary search trees and their implementation. It begins by defining binary trees and their properties. It then describes how binary search trees work, with the key property that for every node, all keys in its left subtree are smaller than the node's key and all keys in its right subtree are larger. It provides pseudocode for basic binary search tree operations like search, insert, delete, find minimum and maximum. Finally, it introduces AVL trees, which are self-balancing binary search trees that ensure fast lookup by keeping the height of left and right subtrees close.

1. Binary Search Tree

2. Preliminaries
Search
Array
List
Stack?
Queue?
For large amounts of input, the linear access
time of lists is prohibitive

3. Preliminaries
Tree
A collection of nodes
The collection can be empty
Otherwise, the tree consists of a distinguished
node r, called the root, and zero or more
(sub)trees T1, T2, T3, …, Tk, each of whose
roots are connected by a directed edge to r.
The root of each subtree is said to be a child
of r, and r is the parent of each subtree root

4. Preliminaries
root
T1 T2 T3 T4 Tk
…

5. Preliminaries
Tree
A tree is a collection of n nodes, one of which
is the root, and n-1 edges.
Each edge connects some node to its parent and
every node except the root has one parent

6. Preliminaries
ROOT
A
INTERNAL NODES INTERNAL NODES
B C D E F G
LEAF LEAF
H I J L M N O
LEAF LEAF LEAVES
P Q
LEAVES

7. Binary Tree
A binary tree is a tree in which no node
can have more than two children
root
TL TR

8. Binary Tree
A
D E
H I J L
P Q

9. Implementation
 Node
class node{
public:
int item;
node *left;
node *right;
node(int x) { item = x; left = right = NULL; }
node( ) { item = 0; left = right = NULL; }
};

10. Expression Trees
(a+b*c)+((d*e+f)*g) +
+ *
a * + g
b c * f
d e

11. Binary Search Tree
 An application of binary trees is their use in
searching
 Let us assume that each node in the tree is
assigned a key value, and assume that this is an
integer
 The property that makes a binary tree into a
binary search tree is that for every node, X, in
the tree, the values of all keys in the left subtree
are smaller than the key value in X, and the
values of all keys in the right subtree are larger
than the key value in X.

12. Binary Search Tree
6 6
2 8 2 8
1 4 1 4
3 3 7

13. Binary Search Tree
class BST{
private:
int size;
node *root;
public:
BST() {size = 0; root = NULL;}
void insert(int);
bool delete(int);
bool search(int);
int minimum();
int maximum();
};

14. Binary Search Tree (Search)
Search for 10
6
2 8
1 4 20
3 10 50

15. Binary Search Tree (Search)
bool BST::search(int x){
node *tmp = root;
while(tmp!=NULL){
if(x == tmp->item)
return true;
if(x < tmp->item)
tmp = tmp->left;
else
tmp = tmp->right;
}
return false;
}

16. Binary Search Tree (Minimum)
6
2 8
1 4 20
-5 3 10 50
-1

17. Binary Search Tree (Minimum)
int BST::minimum(){
node *tmp = root;
while(tmp->left != NULL)
tmp = tmp -> left;
return temp->item;
}

18. Binary Search Tree (Insert)
6
Insert 20, 10, 50
2 8
1 4 20
3 10 50

19. Binary Search Tree (Insert)
Let’s insert 6, 2, 4, 3, 1, 8 and 11 in an
empty BST
6
2 8
1 4 11
3

20. Binary Search Tree (Insert)
Try inserting 1, 2, 3, and 4 in an empty
BST.
1
2
3
4

21. Binary Search Tree (Insert)
void BST::insert(int x){
node *n = new node(x);
node *tmp = root;
if(tmp = NULL)
root = n;
else{
node *tmp2;
while(tmp!=NULL){
tmp2 = tmp;
if(x < tmp->item)
tmp = tmp->left;
else
tmp = tmp->right;
}
if(x < tmp2->item)
tmp2->left = n;
else
tmp2->right = n;
}
}

22. BST (Delete)
In deletion, we don’t ask for a position.
We ask for the actual item that has to be
deleted. Deleting a leaf
6
2 8
4 11
1
Deleting a node with one child
3
Deleting a node with two children

23. Deleting a Leaf (-1)
6
2 8
1 4 20
-5 3 10 50
-1

24. Deleting a Node with a Child(-5)
6
2 8
1 4 20
-5 3 10 50
-1

25. Deleting a node with two
children (2)
6
3
2 8
1 4 20
-5 3 10 50
-1

26. DeleteNode Code
bool BST::deleteNode(int x){
node *del = searchNode(x);
if(del->left == NULL && del->right==NULL)
delete del; //leaf
else{
}
}

27. One Child
if(del->left==NULL)
del = del->right;
else
if(del->right==NULL)
del = del->left;

28. Two Children
else{
node *ptr = minimum(del->right);
int x = ptr->item;
deleteNode(x);
del->item = x;
}

29. Running of Operations
Linear
1
2
3
4

30. Discussion
 We did not achieve our goal of log n.
 Can we improve?
 Always keep the tree balanced A
D E
H I J L
P Q

31. Adelson-Velski Landis (AVL)
Tree
An AVL tree is a binary search tree where
every node of the tree satisfies the
following property:
The height of the left and right subtrees of a
node differs by at most one.

32. Adelson-Velski Landis (AVL)
Tree

33. Adelson-Velski Landis (AVL)
Tree
 In order to properly implement the AVL, the node has to
be redefined.
class node{
public:
int item;
node *left;
node *right;
int height;
node(int x) { item = x; left = right = NULL; }
node( ) { item = 0; left = right = NULL; }
};

34. Adelson-Velski Landis (AVL)
Tree
 What kinds of violations may occur in a regular
BST that will result in height imbalance?
1 3 3
2 2 1
3 1 2

35. Right Rotate
1
2
2
1 3
3

36. Left-Rotate
2
1 3

37. Left-Right Rotate
3
2
1
1 3
2

38. Right-Left Rotate
3 3
2
2 2
1 3
1 1

39. Challenge
Insert the following items in an AVL
10, 20, 30, 40, 50, 60, 70, 80, 71, 61, 51, 41,
31, 21, 11

40. Right Rotate
void BST::rightRotate(node *r){
node *p = r->left;
r->left = p->right;
p->right = r;
//fill in the missing code
}

41. Left Rotate
void BST::leftRotate(node *r){
node *p = r->right;
r->right= p->left;
p->left= r;
//fill in the missing code
}

42. Other Rotations
I leave this as an exercise

43. Insert
void BST::insert(int x){
//do insert as in BST
current = x;
set current to balanced
do{
previous = x;
update height of current
lh = height of the left subtree of current
rh = height of the left subtree of current
set current as left leaning, right leaning, or balanced
if(violation occurs)
perform corresponding rotation
}while(??);
}