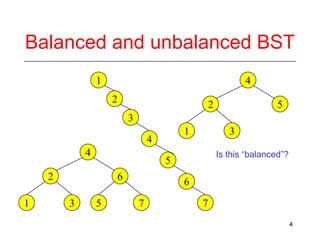
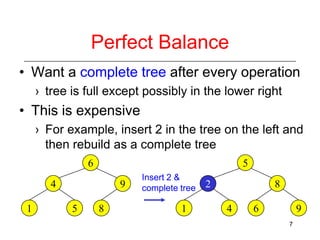
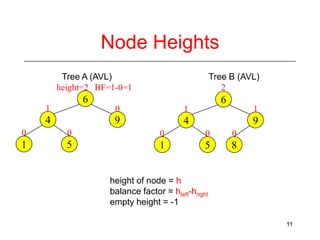
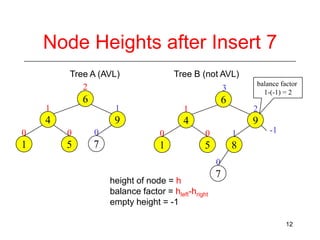
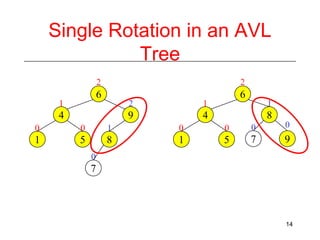
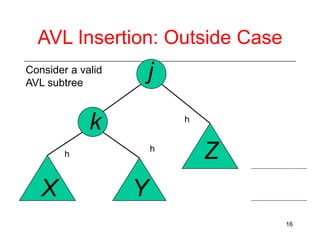
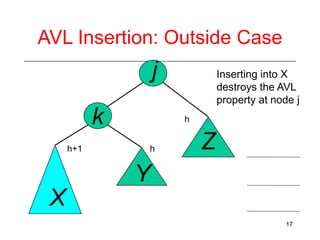
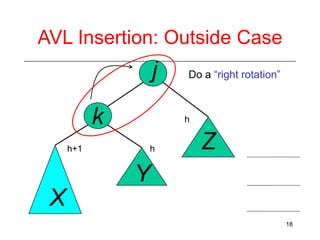
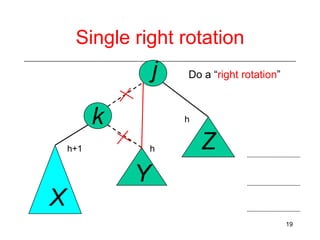
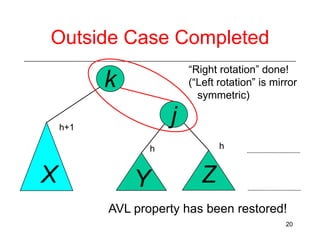
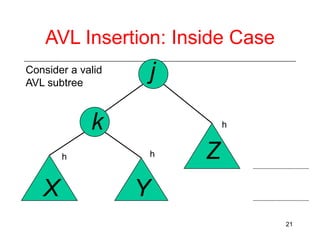
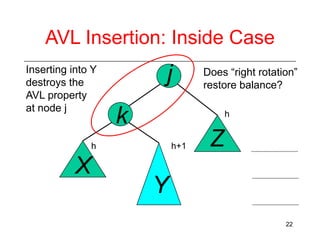
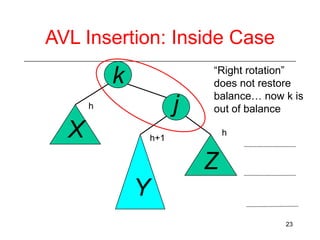
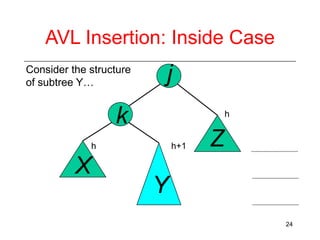
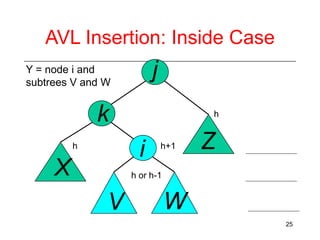
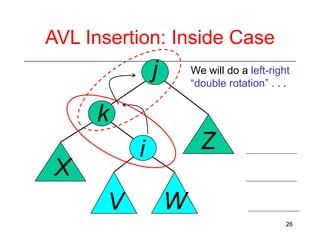
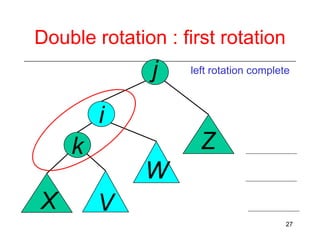
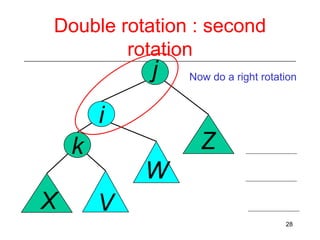
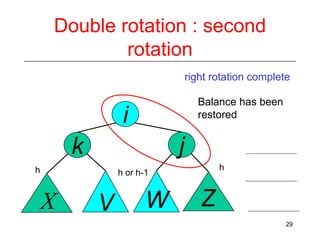
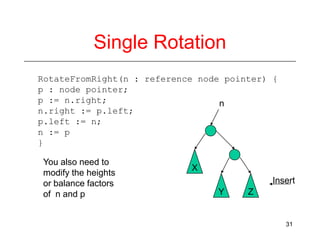
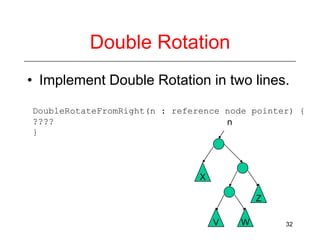
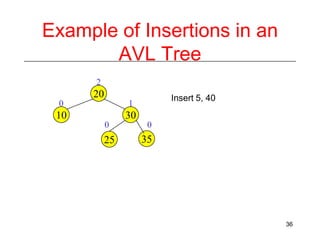
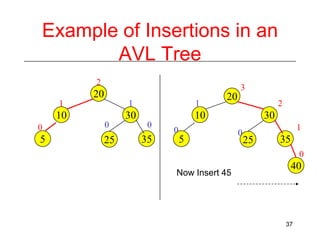
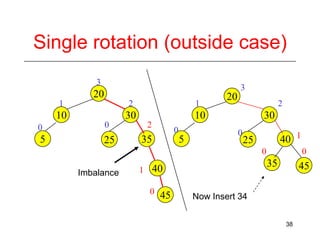
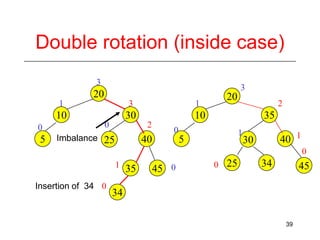
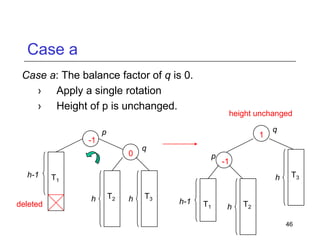
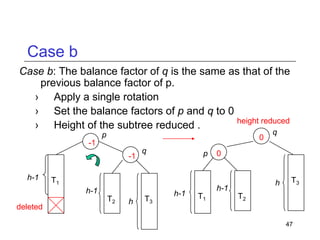
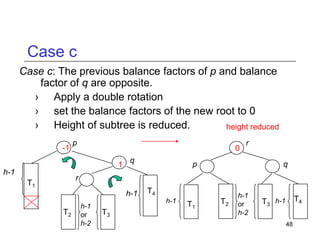
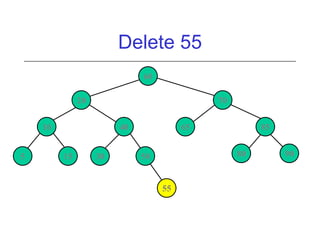
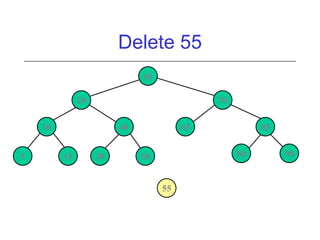
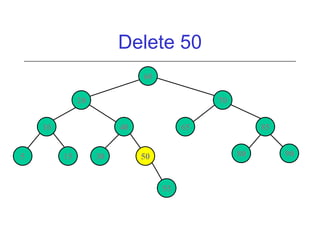
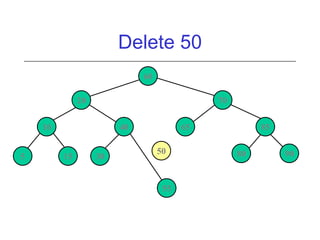
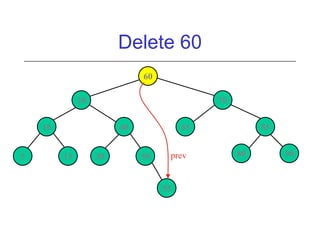
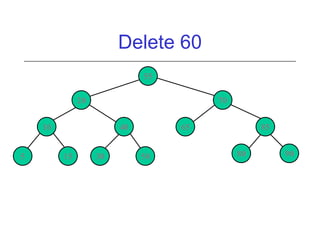
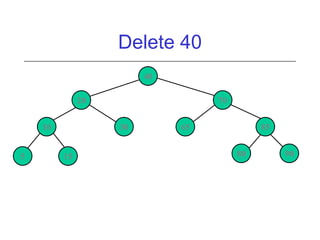
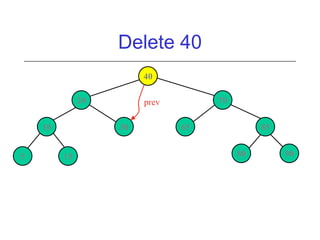
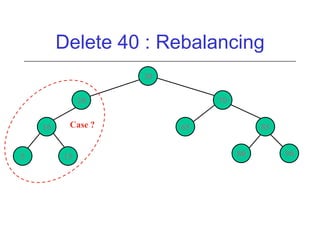
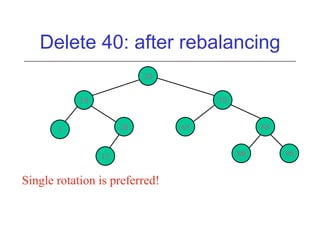
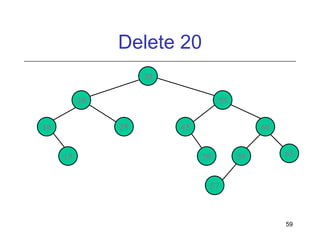
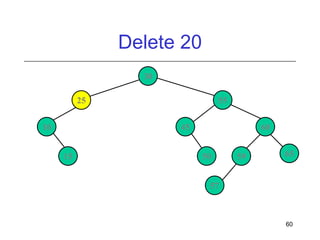
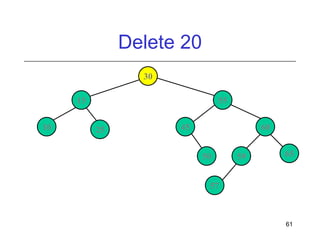
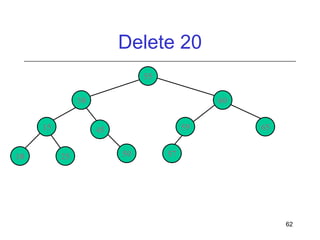
This document discusses AVL trees, which are self-balancing binary search trees. It begins by explaining that binary search trees have O(log N) best case time for operations but can degrade to O(N) in the worst case if the tree becomes unbalanced. The document then introduces AVL trees, which maintain balance by ensuring that the heights of any node's two child subtrees differ by at most one. This guarantees search, insertion, and deletion operations take O(log N) time. The document explains the node height calculation and covers insertion and deletion algorithms in AVL trees through examples, including single and double rotations to rebalance the tree.

1. Advance Data Structures
Lecture 3 AVL Trees

2. Binary Search Tree - Best
Time
• All BST operations are O(h), where h is
tree height
• minimum h is h log 2N for a binary tree
with N nodes
› What is the best case tree?
› What is the worst case tree?
• So, best case running time of BST
operations is O(log N)
2

3. Binary Search Tree - Worst
Time
• Worst case running time is O(N)
› What happens when you Insert elements in
ascending order?
• Insert: 2, 4, 6, 8, 10, 12 into an empty BST
› Problem: Lack of “balance”:
• compare height of left and right subtree
› Unbalanced degenerate tree
3

4. Balanced and unbalanced BST
1
4
2
2
5
3
1
4
4
6
3
Is this “balanced”?
5
2
1
3
5
6
7
7
4

5. Approaches to balancing trees
• Don't balance
› May end up with some nodes very deep
• Strict balance
› The tree must always be balanced perfectly
• Pretty good balance
› Only allow a little out of balance
• Adjust on access
› Self-adjusting
5

6. Balancing Binary Search
Trees
• Many algorithms exist for keeping
binary search trees balanced
› Adelson-Velskii and Landis (AVL) trees
(height-balanced trees)
› Splay trees and other self-adjusting trees
› B-trees and other multiway search trees
6

7. Perfect Balance
• Want a complete tree after every operation
› tree is full except possibly in the lower right
• This is expensive
› For example, insert 2 in the tree on the left and
then rebuild as a complete tree
6
5
4
1
9
5
8
Insert 2 &
complete tree
1
2
8
4
6
9
7

8. AVL - Good but not Perfect
Balance
• AVL trees are height-balanced binary
search trees
• Balance factor of a node
› height(left subtree) - height(right subtree)
• An AVL tree has balance factor
calculated at every node
› For every node, heights of left and right
subtree can differ by no more than 1
› Store current heights in each node
8

9. Height of an AVL Tree
• N(h) = minimum number of nodes in an
AVL tree of height h.
• Basis
› N(0) = 1, N(1) = 2
• Induction
h
› N(h) = N(h-1) + N(h-2) + 1
• Solution (recall Fibonacci analysis)
› N(h) >
h
(
1.62)
h-1
h-2
9

10. Height of an AVL Tree
• N(h) > h (
1.62)
• Suppose we have n nodes in an AVL
tree of height h.
› n > N(h) (because N(h) was the minimum)
› n > h hence log n > h (relatively well
balanced tree!!)
› h < 1.44 log2n (i.e., Find takes O(logn))
10

11. Node Heights
Tree A (AVL)
height=2 BF=1-0=1
Tree B (AVL)
2
6
6
1
0
1
1
4
9
4
9
0
0
0
0
0
1
5
1
5
8
height of node = h
balance factor = hleft-hright
empty height = -1
11

12. Node Heights after Insert 7
Tree A (AVL)
2
Tree B (not AVL)
balance factor
1-(-1) = 2
3
6
6
1
1
1
2
4
9
4
9
0
0
0
0
0
1
1
5
7
1
5
-1
8
0
height of node = h
balance factor = hleft-hright
empty height = -1
7
12

13. Insert and Rotation in AVL
Trees
• Insert operation may cause balance factor
to become 2 or –2 for some node
› only nodes on the path from insertion point to
root node have possibly changed in height
› So after the Insert, go back up to the root
node by node, updating heights
› If a new balance factor (the difference hlefthright) is 2 or –2, adjust tree by rotation around
the node
13

14. Single Rotation in an AVL
Tree
2
2
6
6
1
2
1
1
4
9
4
8
0
0
1
0
0
0
0
1
5
8
1
5
7
9
0
7
14

15. Insertions in AVL Trees
Let the node that needs rebalancing be .
There are 4 cases:
Outside Cases (require single rotation) :
1. Insertion into left subtree of left child of .
2. Insertion into right subtree of right child of .
Inside Cases (require double rotation) :
3. Insertion into right subtree of left child of .
4. Insertion into left subtree of right child of .
The rebalancing is performed through four
separate rotation algorithms.
15

16. AVL Insertion: Outside Case
Consider a valid
AVL subtree
j
k
h
h
h
X
Z
Y
16

17. AVL Insertion: Outside Case
j
k
h+1
Inserting into X
destroys the AVL
property at node j
h
h
Z
Y
X
17

18. AVL Insertion: Outside Case
j
k
h+1
Do a “right rotation”
h
h
Z
Y
X
18

19. Single right rotation
j
k
h+1
Do a “right rotation”
h
h
Z
Y
X
19

20. Outside Case Completed
“Right rotation” done!
(“Left rotation” is mirror
symmetric)
k
j
h+1
h
h
X
Y
Z
AVL property has been restored!
20

21. AVL Insertion: Inside Case
Consider a valid
AVL subtree
j
k
h
X
h
h
Z
Y
21

22. AVL Insertion: Inside Case
Inserting into Y
destroys the
AVL property
at node j
j
k
h
h
X
Does “right rotation”
restore balance?
h+1
Z
Y
22

23. AVL Insertion: Inside Case
k
j
h
X
“Right rotation”
does not restore
balance… now k is
out of balance
h
h+1
Z
Y
23

24. AVL Insertion: Inside Case
Consider the structure
of subtree Y…
j
k
h
h
X
h+1
Z
Y
24

25. AVL Insertion: Inside Case
j
Y = node i and
subtrees V and W
k
h
i
h
X
h+1
Z
h or h-1
V
W
25

26. AVL Insertion: Inside Case
j
We will do a left-right
“double rotation” . . .
k
Z
i
X
V
W
26

27. Double rotation : first rotation
j
left rotation complete
i
Z
k
W
X
V
27

28. Double rotation : second
rotation
j
Now do a right rotation
i
Z
k
W
X
V
28

29. Double rotation : second
rotation
right rotation complete
Balance has been
restored
i
j
k
h
h
h or h-1
X
V
W
Z
29

30. Implementation
balance (1,0,-1)
key
left
right
No need to keep the height; just the difference in height,
i.e. the balance factor; this has to be modified on the path of
insertion even if you don’t perform rotations
Once you have performed a rotation (single or double) you won’t
need to go back up the tree
30

31. Single Rotation
RotateFromRight(n : reference node pointer) {
p : node pointer;
p := n.right;
n
n.right := p.left;
p.left := n;
n := p
}
You also need to
modify the heights
or balance factors
of n and p
X
Insert
Y
Z
31

32. Double Rotation
• Implement Double Rotation in two lines.
DoubleRotateFromRight(n : reference node pointer) {
????
n
}
X
Z
V
W
32

33. Insertion in AVL Trees
• Insert at the leaf (as for all BST)
› only nodes on the path from insertion point to
root node have possibly changed in height
› So after the Insert, go back up to the root
node by node, updating heights
› If a new balance factor (the difference hlefthright) is 2 or –2, adjust tree by rotation around
the node
33

34. Insert in BST
Insert(T : reference tree pointer, x : element) : integer {
if T = null then
T := new tree; T.data := x; return 1;//the links to
//children are null
case
T.data = x : return 0; //Duplicate do nothing
T.data > x : return Insert(T.left, x);
T.data < x : return Insert(T.right, x);
endcase
}
34

35. Insert in AVL trees
Insert(T : reference tree pointer, x : element) : {
if T = null then
{T := new tree; T.data := x; height := 0; return;}
case
T.data = x : return ; //Duplicate do nothing
T.data > x : Insert(T.left, x);
if ((height(T.left)- height(T.right)) = 2){
if (T.left.data > x ) then //outside case
T = RotatefromLeft (T);
else
//inside case
T = DoubleRotatefromLeft (T);}
T.data < x : Insert(T.right, x);
code similar to the left case
Endcase
T.height := max(height(T.left),height(T.right)) +1;
return;
}
35

36. Example of Insertions in an
AVL Tree
2
20
0
10
Insert 5, 40
1
30
0
25
0
35
36

37. Example of Insertions in an
AVL Tree
2
3
20
1
1
1
10
30
20
10
0
0
5
25
0
35
0
5
2
30
0
1
25
35
0
Now Insert 45
40
37

38. Single rotation (outside case)
3
3
20
1
2
1
10
30
20
10
0
0
5
25
2
35
0
5
2
30
0
40 1
25
0
Imbalance
35
1 40
0 45
0
45
Now Insert 34
38

39. Double rotation (inside case)
3
3
20
1
5
1
10
0
3
30
20
10
0
2
Imbalance 25
35
0
40
2
1
5
40 1
30
0
1 35
Insertion of 34 0
45 0
0 25
34
45
34
39

40. Extended Example
Insert 3,2,1,4,5,6,7, 16,15,14

41. AVL Tree Deletion
• Similar but more complex than insertion
› Rotations and double rotations needed to
rebalance
› Imbalance may propagate upward so that
many rotations may be needed.
41

42. Deletion of a Node
• Deletion of a node x from an AVL tree
requires the same basic ideas, including
single and double rotations, that are
used for insertion.
• With each node of the AVL tree is
associated a balance factor that is left
high, equal or right high according,
respectively, as the left subtree has
height greater than, equal to, or less
than that of the right subtree.
42

43. Method
1. Reduce the problem to the case when the
node x to be deleted has at most one child.
›
›
If x has two children replace it with its immediate
predecessor y under inorder traversal (the
immediate successor would be just as good)
Delete y from its original position, by proceeding as
follows, using y in place of x in each of the following
steps.
43

44. Method (cont.)
2.
Delete the node x from the tree.
› We’ll trace the effects of this change on height through all the
nodes on the path from x back to the root.
› The action to be taken at each node depends on
•
•
balance factor of the node
sometimes the balance factor of a child of the node.
44

45. Rebalancing the tree
Let p be the node whose balance factor becomes 2 or -2.
› Rotation is needed.
› Let q be the root of the taller subtree of p. We
have three cases according to the balance factor
of q.
45

46. Case a
Case a: The balance factor of q is 0.
› Apply a single rotation
› Height of p is unchanged.
height unchanged
p
1
-1
0
h-1
deleted
q
q
p
-1
T1
h
h
T2
h
T3
h-1
T1
h
T3
T2
46

47. Case b
Case b: The balance factor of q is the same as that of the
previous balance factor of p.
› Apply a single rotation
› Set the balance factors of p and q to 0
height reduced
› Height of the subtree reduced .
p
0
-1
-1
h-1
q
T1
h-1
deleted
p
T2
h
T3
h-1
0
h
h-1
T1
q
T3
T2
47

48. Case c
Case c: The previous balance factors of p and balance
factor of q are opposite.
› Apply a double rotation
› set the balance factors of the new root to 0
› Height of subtree is reduced.
height reduced
-1
p
0
1
h-1
q
r
p
q
r
T1
h-1
T2
h-1
or
h-2
T4
h-1
T3
T1
T2
h-1
or
h-2
T4
T3 h-1
48

49. Delete 55
60
20
70
10
5
40
15
30
65
85
80
50
55
90

50. Delete 55
60
20
70
10
5
40
15
30
65
85
80
50
55
90

51. Delete 50
60
20
70
10
5
40
15
30
65
85
80
50
55
90

52. Delete 50
60
20
70
10
5
40
15
30
65
50
55
85
80
90

53. Delete 60
60
20
70
10
5
40
15
30
65
50
prev
55
85
80
90

54. Delete 60
55
20
70
10
5
40
15
30
65
50
85
80
90

55. Delete 40
40
20
10
5
70
30
15
65
85
80
90

56. Delete 40
40
20
10
5
30
15
70
prev
65
85
80
90

57. Delete 40 : Rebalancing
30
20
10
5
Case ?
15
70
65
85
80
90

58. Delete 40: after rebalancing
30
10
70
20
5
15
Single rotation is preferred!
65
85
80
90

59. Delete 20
30
20
10
55
25
15
45
60
50
59
65
57
59

60. Delete 20
30
25
10
55
45
15
60
50
59
65
57
60

61. Delete 20
30
15
10
55
25
45
60
50
59
65
57
61

62. Delete 20
55
30
15
10
60
59
45
25
50
65
57
62

63. Pros and Cons of AVL Trees
Arguments for AVL trees:
1. Search is O(log N) since AVL trees are always balanced.
2. Insertion and deletions are also O(logn)
3. The height balancing adds no more than a constant factor to the
speed of insertion.
Arguments against using AVL trees:
1. Difficult to program & debug; more space for balance factor.
2. Asymptotically faster but rebalancing costs time.
3. Most large searches are done in database systems on disk and use
other structures (e.g. B-trees).
4. May be OK to have O(N) for a single operation if total run time for
many consecutive operations is fast (e.g. Splay trees).
63

64. Double Rotation Solution
DoubleRotateFromRight(n : reference node pointer) {
RotateFromLeft(n.right);
n
RotateFromRight(n);
}
X
Z
V
W
64