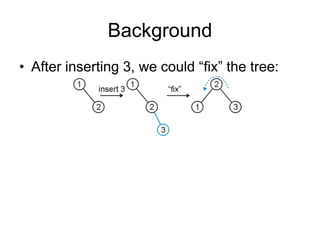
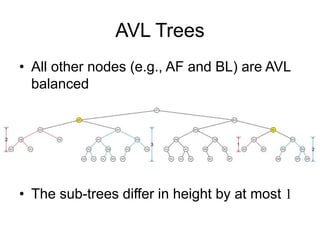
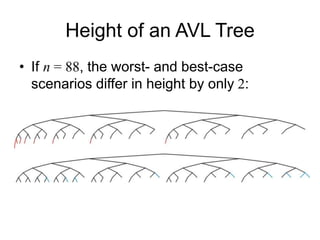
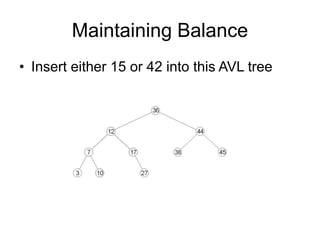
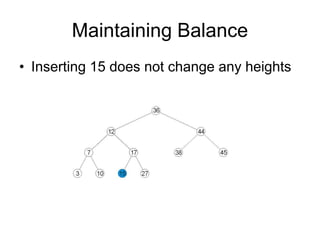
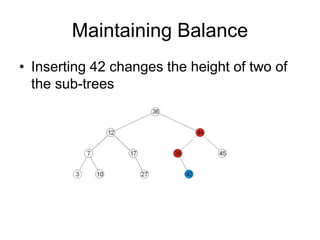
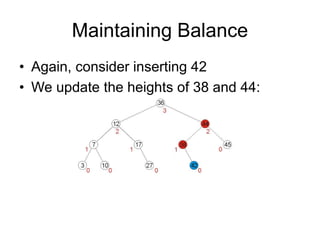
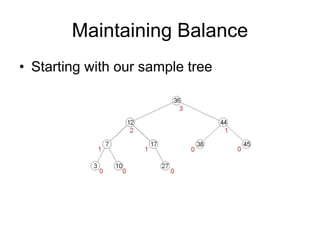
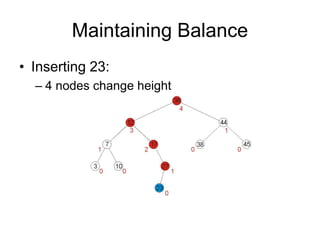
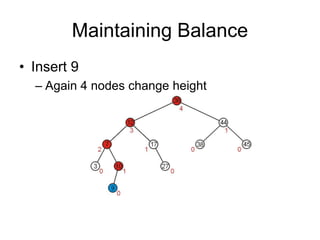
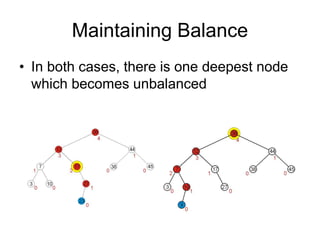
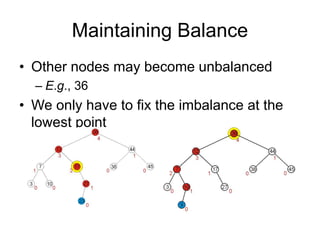
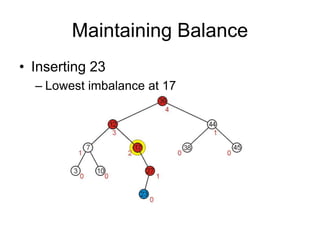
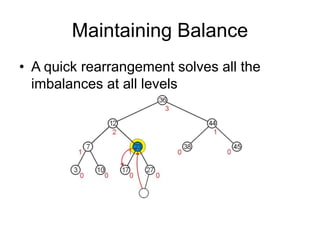
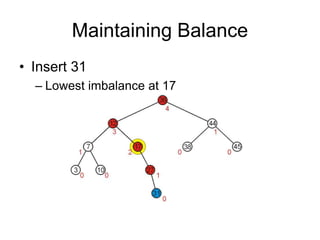
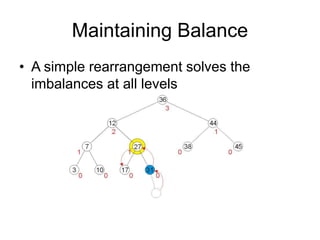
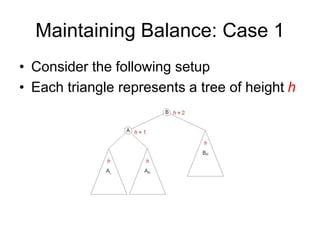
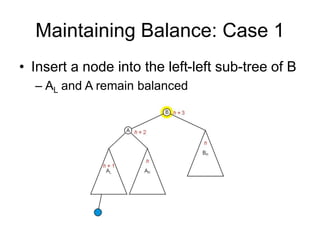
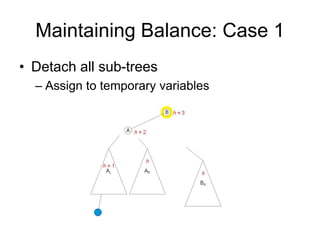
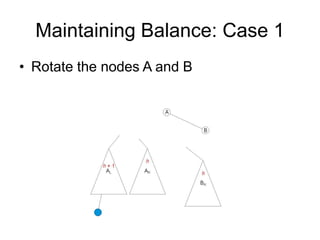
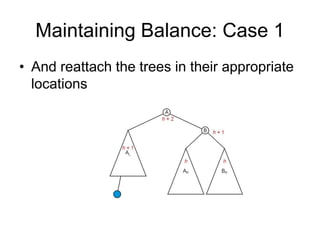
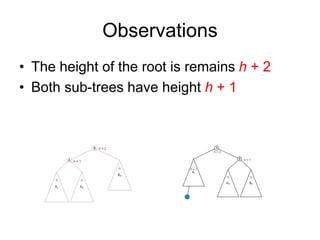
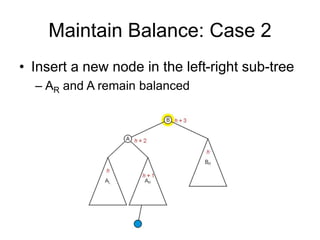
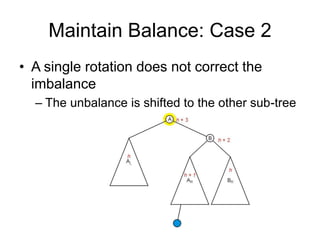
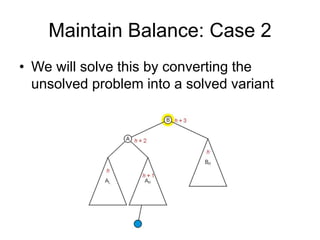
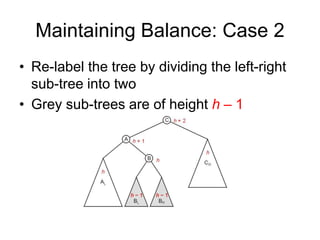
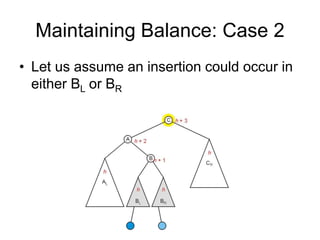
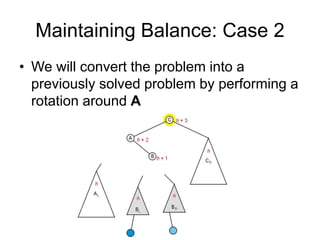
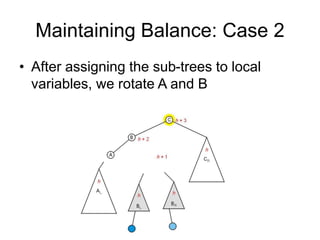
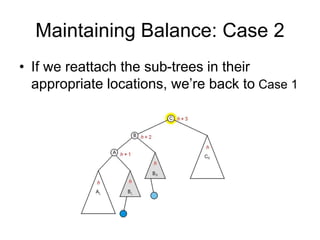
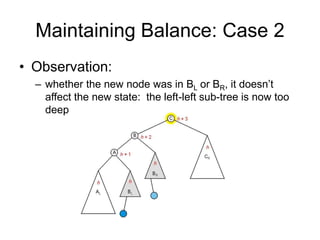
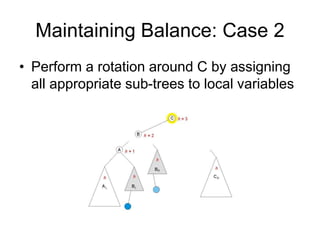
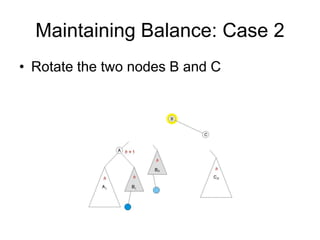
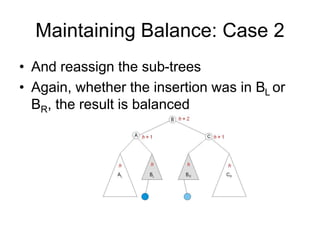
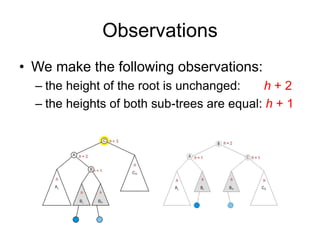
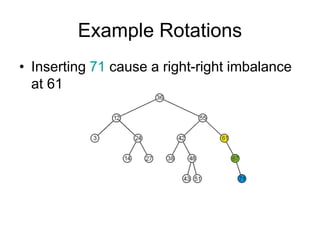
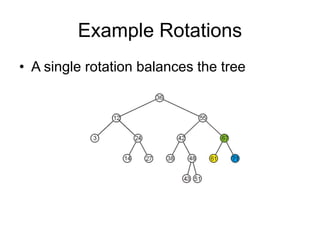
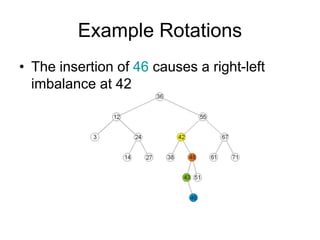
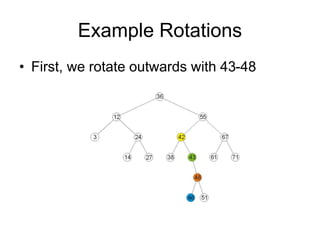
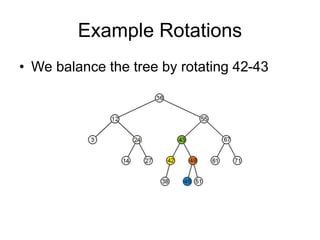
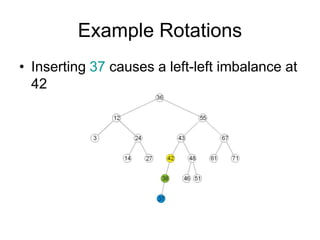
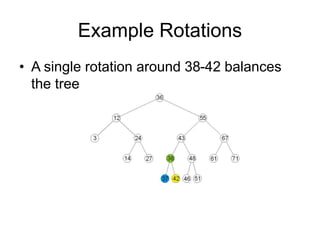
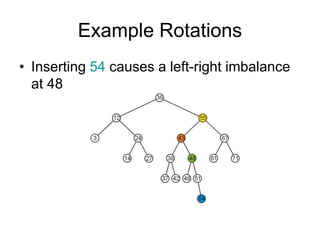
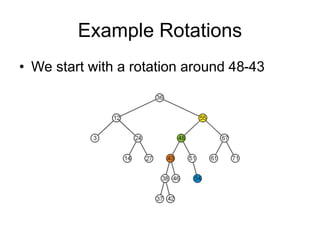
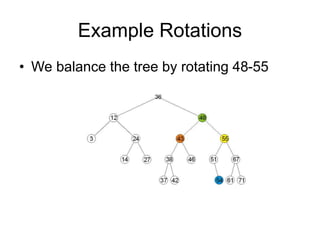
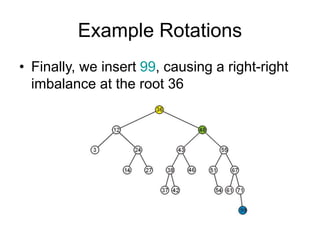
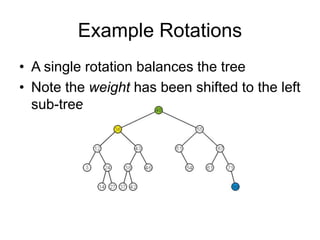
AVL trees are self-balancing binary search trees. They ensure that the heights of the two subtrees of any node differ by at most one. This balance property is maintained during insertions and deletions via rotations. There are two types of rotations needed - a single rotation to balance nodes where the imbalance is on one side, and a double rotation to balance nodes where the imbalance is on both sides. All operations on AVL trees, including rotations, take O(log n) time, making them efficient for search, insertion, and deletion.

1. AVL Trees
Douglas Wilhelm Harder
Department of Electrical and Computer Engineering
University of Waterloo
Copyright © 2006-8 by Douglas Wilhelm Harder. All rights reserved.
ECE 250 Data Structures and Algorithms

2. Outline
• Background
• Define balance
• Maintaining balance within a tree
– AVL trees
– difference of heights
– rotations

3. Background
• From previous lectures:
– Binary search trees store ordered data
– Best case height: Q(ln(n))
– Worst case height: O(n)
• Requirement:
– That tree is balanced

4. Background
• After inserting 3, we could “fix” the tree:

5. AVL Trees
• We will focus on the first strategy:
AVL trees
• Named after Adelson-Velskii and Landis
• Balance is defined by comparing the
height of the two sub-trees of a node

6. AVL Trees
• Recall:
– An empty tree has height –1
– A tree with a single node has height 0

7. AVL Trees
• A binary search tree is said to be AVL
balanced if:
– The difference in the heights between the left
and right sub-trees is at most 1, and
– Both sub-trees are themselves AVL trees

8. AVL Trees
• AVL trees with 1, 2, 3, and 4 nodes:

9. AVL Trees
• Here is a larger AVL tree (42 nodes):

10. AVL Trees
• The root node is AVL-balanced because
both sub-trees are of height 4:

11. AVL Trees
• All other nodes (e.g., AF and BL) are AVL
balanced
• The sub-trees differ in height by at most 1

12. Height of an AVL Tree
• By the definition of complete trees, any
complete binary search tree is an AVL tree
• Thus an upper bound on the number of
nodes in an AVL tree of height h a perfect
binary tree with 2h + 1 – 1 nodes
• What is an lower bound?

13. Height of an AVL Tree
• Let F(h) be the fewest number of nodes in
a tree of height h
• From a previous slide:
F(0) = 1
F(1) = 2
• Can we find F(h)?

14. Height of an AVL Tree
• The worst-case AVL tree of height h would
have:
– A worst-case AVL tree of height h – 1 on one
side,
– A worst-case AVL tree of height h – 2 on the
other, and
– The root node
• We get: F(h) = F(h – 1) + F(h – 2) + 1

15. Height of an AVL Tree
• This is a recurrence relation:
• The solution?













1
1
)
2
F(
)
1
F(
1
2
0
1
)
F(
h
h
h
h
h
h

16. Height of an AVL Tree
• Use Maple:
> rsolve( {F(0) = 1, F(1) = 2,
F(h) = 1 + F(h - 1) + F(h - 2)}, F(h) );
> asympt( %, h );
   









3 5
10
1
2









1
2
5
2
h









1
2
3 5
10









1
2
5
2
h 2 5









2

1 5
h
5 ( )

1 5
2 5









2

1 5
h
5 ( )

1 5
1
 
( )

3 5 5 ( )

1 5
h
5 ( )
 
1 5 2
h
1
1
5
e
( )
h  I
( )
 
5 3 5 2
h
( )

1 5 ( )

1 5
h

17. Height of an AVL Tree
• This is approximately
F(h) ≈ 1.8944 fh
where f ≈ 1.6180 is the golden ratio
– That is, F(h) = W(fh)
• Thus, we may invert this to find the
maximum value of h for a given n:
logf( n / 1.8944 ) = logf( n ) – 1.3277

18. Height of an AVL Tree
• If n = 88, the worst- and best-case
scenarios differ in height by only 2:

19. Height of an AVL Tree
• If n = 106, the bounds on h are:
– The minimum height: log2( 106 ) – 1 ≈ 19
– the maximum height : logf( 106 / 1.8944 ) < 28

20. Maintaining Balance
• To maintain AVL balance, observe that:
– Inserting a node can increase the height of a
tree by at most 1
– Removing a node can decrease the height of
a tree by at most 1

21. Maintaining Balance
• Insert either 15 or 42 into this AVL tree

22. Maintaining Balance
• Inserting 15 does not change any heights

23. Maintaining Balance
• Inserting 42 changes the height of two of
the sub-trees

24. Maintaining Balance
• To calculate changes in height, the
member function must run in O(1) time
• Our implementation of height is O(n):
template <typename Comparable>
int BinarySearchNode<Comparable>::height() const {
return max(
( left() == 0 ) ? 0 : 1 + left() -> height(),
( right() == 0 ) ? 0 : 1 + right() -> height()
);
}

25. Maintaining Balance
• Introduce a member variable
int tree_height;
• The member function is now:
template <typename Comparable>
int BinarySearchNode<Comparable>::height() const {
return tree_height;
}

26. Maintaining Balance
• Only insert and remove may change the
height
– This is the only place we need to update the
height
– These algorithms are already recursive

27. Insert
template <typename Comparable>
void AVLNode<Comparable>::insert( const Comparable & obj ) {
if ( obj < element ) {
if ( left() == 0 ) {
left_tree = new AVLNode<Comparable>( obj );
tree_height = 1;
} else {
left() -> insert( obj );
tree_height = max( tree_height, 1 + left()->height() );
}
} else if ( obj > element ) {
// ...
}
}

28. Maintaining Balance
• Using the same, tree, we mark the stored
heights:

29. Maintaining Balance
• Again, consider inserting 42
• We update the heights of 38 and 44:

30. Maintaining Balance
• If a tree is AVL balanced, for an insertion
to cause an imbalance:
– The heights of the sub-trees must differ by 1
– The insertion must increase the height of the
deeper sub-tree by 1

31. Maintaining Balance
• Starting with our sample tree

32. Maintaining Balance
• Inserting 23:
– 4 nodes change height

33. Maintaining Balance
• Insert 9
– Again 4 nodes change height

34. Maintaining Balance
• In both cases, there is one deepest node
which becomes unbalanced

35. Maintaining Balance
• Other nodes may become unbalanced
– E.g., 36
• We only have to fix the imbalance at the
lowest point

36. Maintaining Balance
• Inserting 23
– Lowest imbalance at 17

37. Maintaining Balance
• A quick rearrangement solves all the
imbalances at all levels

38. Maintaining Balance
• Insert 31
– Lowest imbalance at 17

39. Maintaining Balance
• A simple rearrangement solves the
imbalances at all levels

40. Maintaining Balance: Case 1
• Consider the following setup
• Each triangle represents a tree of height h

41. Maintaining Balance: Case 1
• Insert a node into the left-left sub-tree of B
– AL and A remain balanced

42. Maintaining Balance: Case 1
• Detach all sub-trees
– Assign to temporary variables

43. Maintaining Balance: Case 1
• Rotate the nodes A and B

44. Maintaining Balance: Case 1
• And reattach the trees in their appropriate
locations

45. Observations
• The height of the root is remains h + 2
• Both sub-trees have height h + 1

46. Maintain Balance: Case 2
• Insert a new node in the left-right sub-tree
– AR and A remain balanced

47. Maintain Balance: Case 2
• A single rotation does not correct the
imbalance
– The unbalance is shifted to the other sub-tree

48. Maintain Balance: Case 2
• We will solve this by converting the
unsolved problem into a solved variant

49. Maintaining Balance: Case 2
• Re-label the tree by dividing the left-right
sub-tree into two
• Grey sub-trees are of height h – 1

50. Maintaining Balance: Case 2
• Let us assume an insertion could occur in
either BL or BR

51. Maintaining Balance: Case 2
• We will convert the problem into a
previously solved problem by performing a
rotation around A

52. Maintaining Balance: Case 2
• After assigning the sub-trees to local
variables, we rotate A and B

53. Maintaining Balance: Case 2
• If we reattach the sub-trees in their
appropriate locations, we’re back to Case 1

54. Maintaining Balance: Case 2
• Observation:
– whether the new node was in BL or BR, it doesn’t
affect the new state: the left-left sub-tree is now too
deep

55. Maintaining Balance: Case 2
• Perform a rotation around C by assigning
all appropriate sub-trees to local variables

56. Maintaining Balance: Case 2
• Rotate the two nodes B and C

57. Maintaining Balance: Case 2
• And reassign the sub-trees
• Again, whether the insertion was in BL or
BR, the result is balanced

58. Observations
• We make the following observations:
– the height of the root is unchanged: h + 2
– the heights of both sub-trees are equal: h + 1

59. Rotations: Summary
• There are two symmetric cases to those
we have examined:
– insertions into either the
• left-left sub-tree or the right-right sub-tree
which cause an imbalance require a single
rotation to balance the node
– insertions into either the
• left-right sub-tree or the right-left sub-tree
which cause an imbalance require two
rotations to balance the node

60. Insert (Implementation)
template <typename Comparable>
void AVLNode<Comparable>::insert( const Comparable & obj ) {
if ( obj < element ) {
if ( left() == 0 ) {
// cannot cause an AVL imbalance
left_tree = new BinarySearchNode<Comparable>( obj );
tree_height = 1;
} else {
left() -> insert( obj );
if ( left()->height() – right()->height() == 2 ) {
AVLNode<Comparable> * AL = left-left sub-tree
AVLNode<Comparable> * AR = left-right sub-tree
AVLNode<Comparable> * BR = right sub-tree
swap elements of nodes A and B
reassign sub-trees in their appropriate locations
updates heights of nodes A and B
}
}
} else if ( obj > element ) {
// ...

61. Insertion (Implementation)
• Comments:
– All the rotation statements are Q(1)
– An insertion requires at most 2 rotations
– All insertions are still Q(ln(n))
– It is possible to tighten the previous code
– Aside
• if you want to explicitly rotate the nodes A and B,
you must also pass a reference to the parent
pointer as an argument:
insert( Object obj, AVLNode<Comparable> * & parent )

62. Example Rotations
• Consider the following AVL tree

63. Example Rotations
• Usually an insertion does not require a
rotation

64. Example Rotations
• Inserting 71 cause a right-right imbalance
at 61

65. Example Rotations
• A single rotation balances the tree

66. Example Rotations
• The insertion of 46 causes a right-left
imbalance at 42

67. Example Rotations
• First, we rotate outwards with 43-48

68. Example Rotations
• We balance the tree by rotating 42-43

69. Example Rotations
• Inserting 37 causes a left-left imbalance at
42

70. Example Rotations
• A single rotation around 38-42 balances
the tree

71. Example Rotations
• Inserting 54 causes a left-right imbalance
at 48

72. Example Rotations
• We start with a rotation around 48-43

73. Example Rotations
• We balance the tree by rotating 48-55

74. Example Rotations
• Finally, we insert 99, causing a right-right
imbalance at the root 36

75. Example Rotations
• A single rotation balances the tree
• Note the weight has been shifted to the left
sub-tree

76. AVL Trees as Arrays?
• We previously saw that:
– Complete tree can be stored using an array
– An arbitrary tree of n nodes requires O(2n)
memory
• Is it possible to store an AVL tree as an
array and not require exponentially more
memory?

77. AVL Trees as Arrays?
• Recall that in the worst case, an AVL tree
of n nodes has a height at most
logf(n) – 1.3277
• Such a tree requires an array of size
2logf(n) – 1.3277 + 1 – 1
• We can rewrite this as
2–0.3277 nlogf(2) ≈ 0.7968 n1.44
• Thus, we would require O(n1.44) memory

78. AVL Trees as Arrays?
• While the polynomial behaviour of n1.44 is
not as bad as exponential behaviour, it is
still reasonably sub-optimal when
compared to the linear
growth associated with
node-based trees
• This plot shows
n n1.44
for n = [0, 1000]

79. Summary
• In this topic we have covered:
– Insertions and removals are like binary search
trees
– With each insertion or removal there is at
most one correction required
• a single rotation, or
• a double rotation;
which runs in O(1) time
– Depth is O( ln(n) )
∴ all operations are O( ln(n) )

80. Usage Notes
• These slides are made publicly available on the web for
anyone to use
• If you choose to use them, or a part thereof, for a course
at another institution, I ask only three things:
– that you inform me that you are using the slides,
– that you acknowledge my work, and
– that you alert me of any mistakes which I made or changes
which you make, and allow me the option of incorporating such
changes (with an acknowledgment) in my set of slides
Sincerely,
Douglas Wilhelm Harder, MMath
dwharder@alumni.uwaterloo.ca