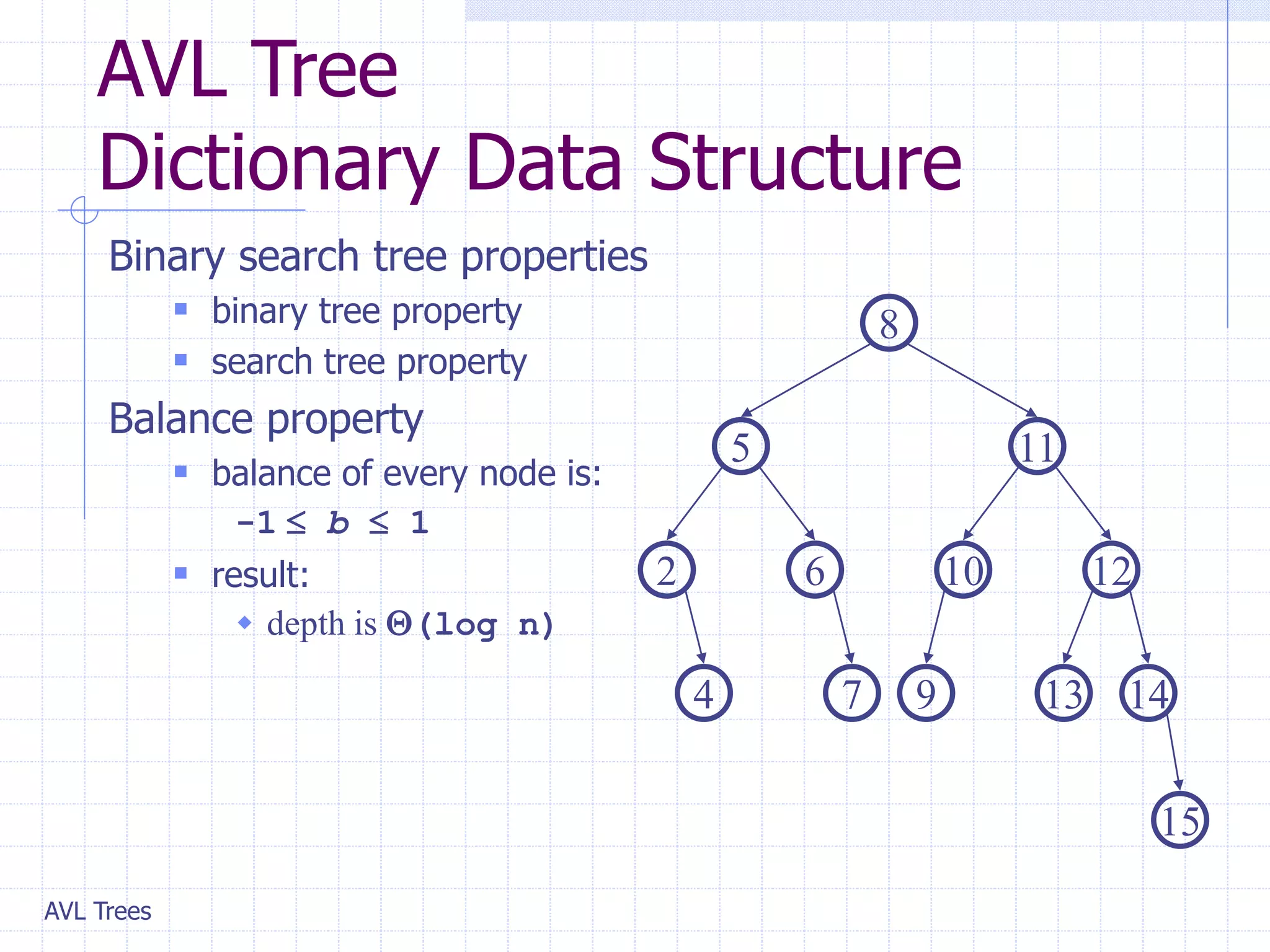
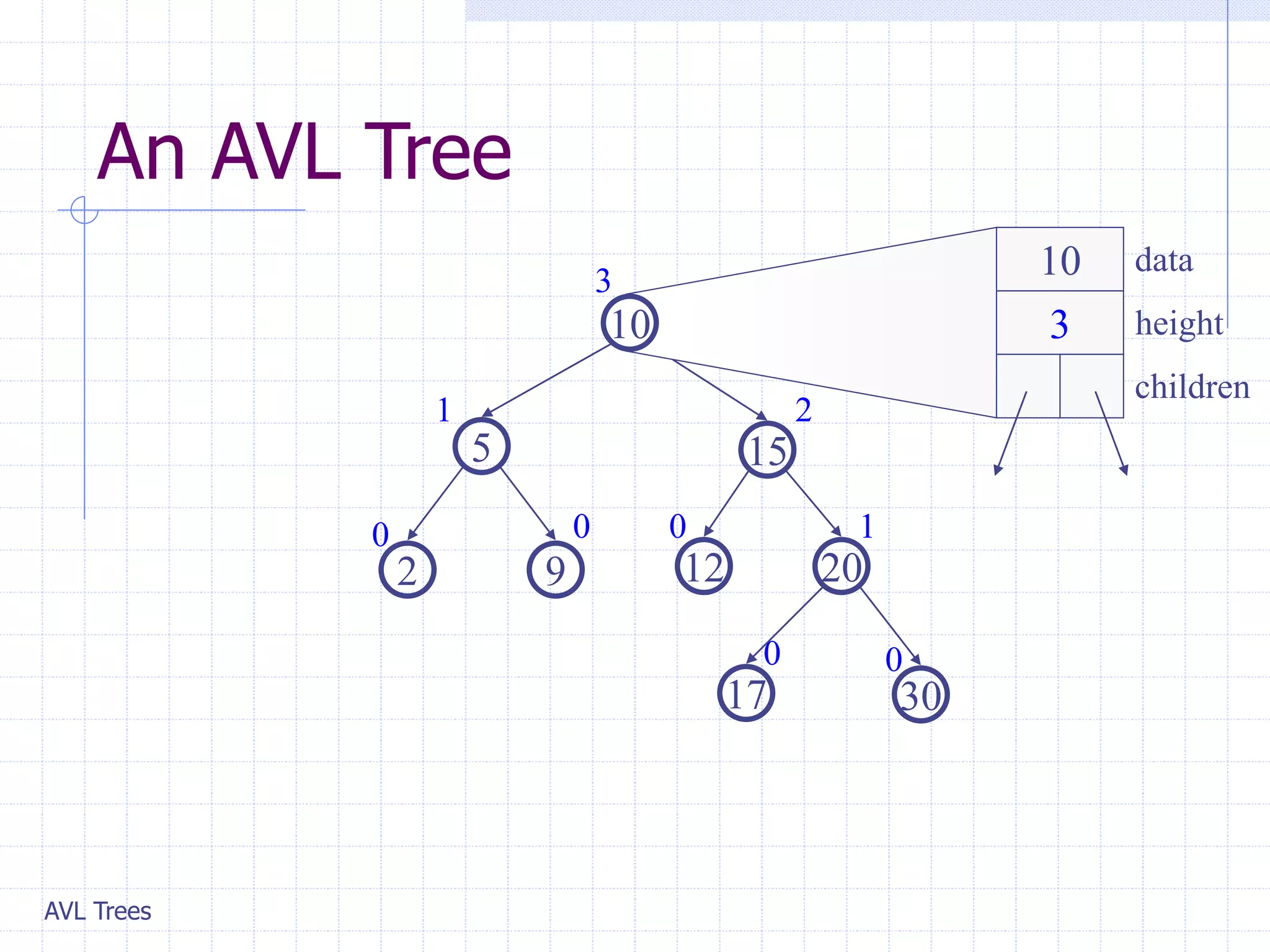
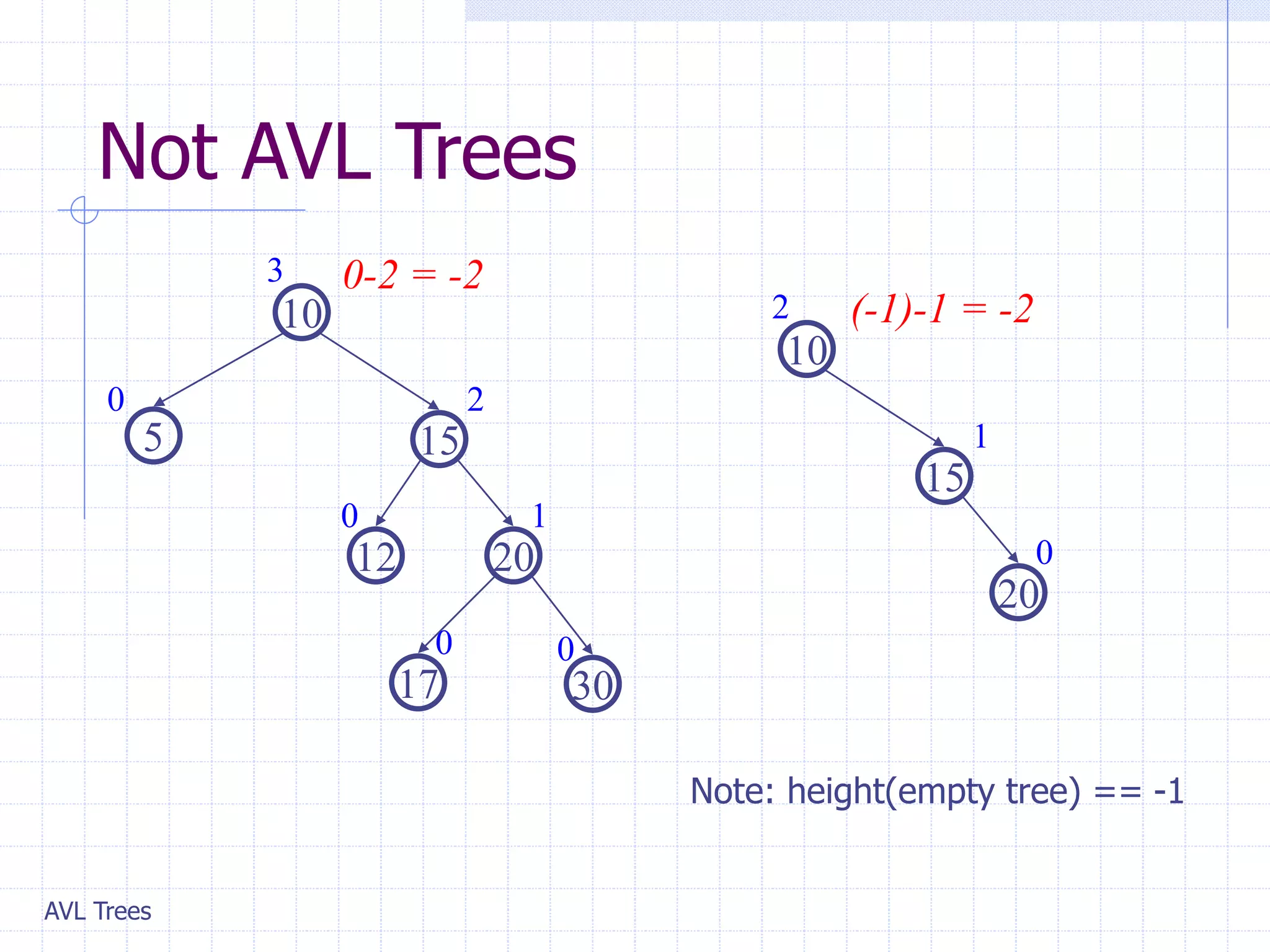
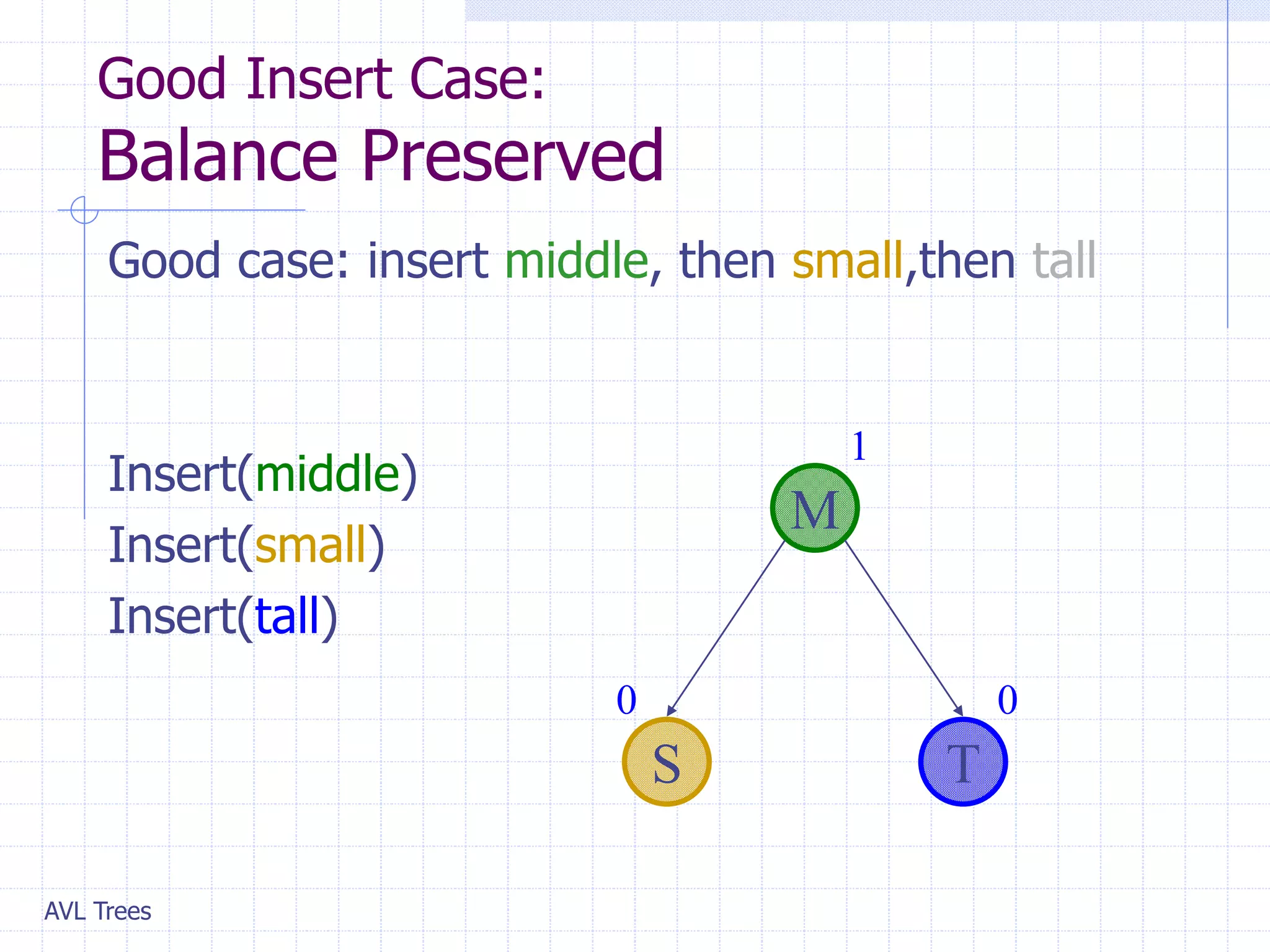
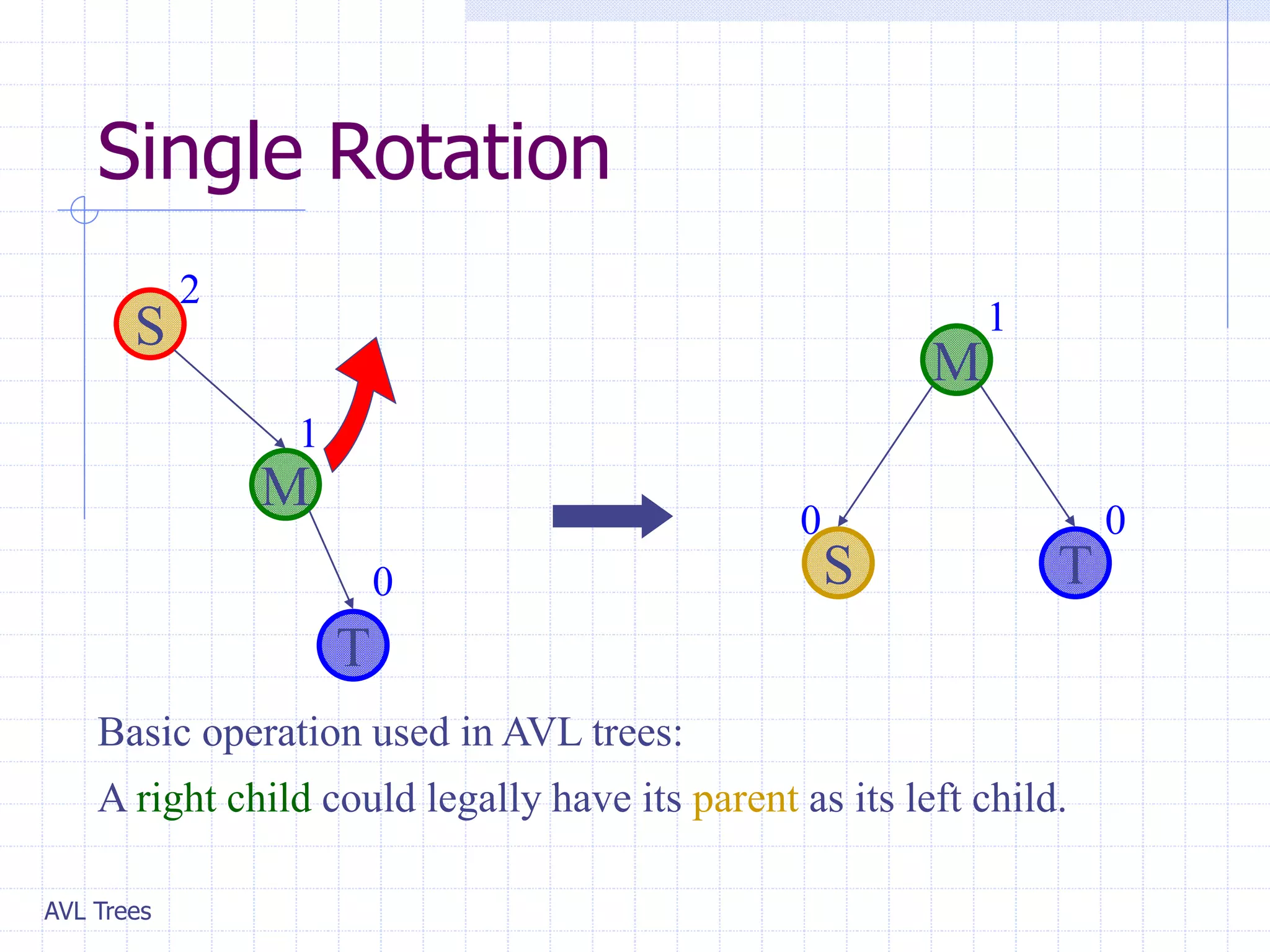
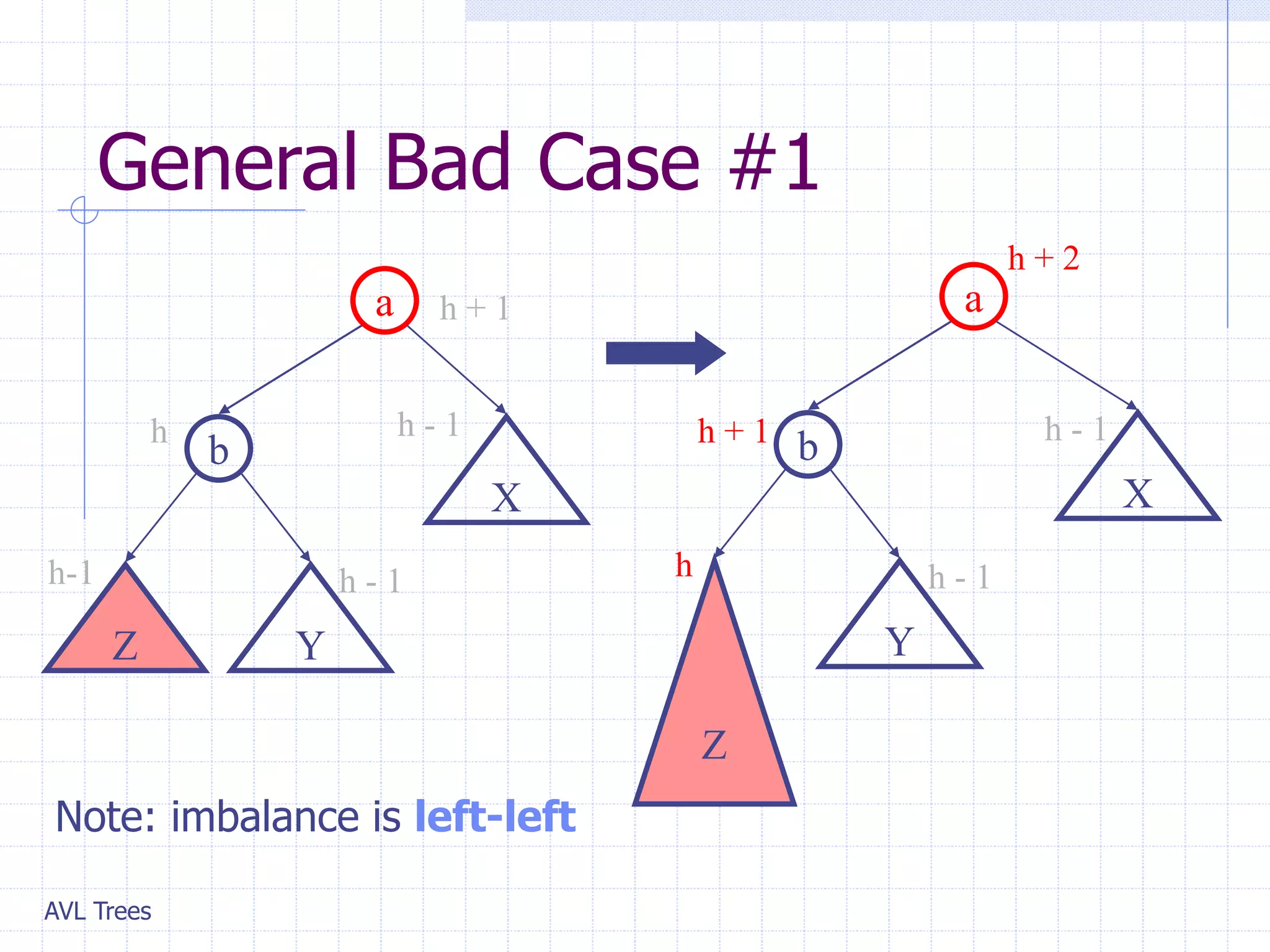
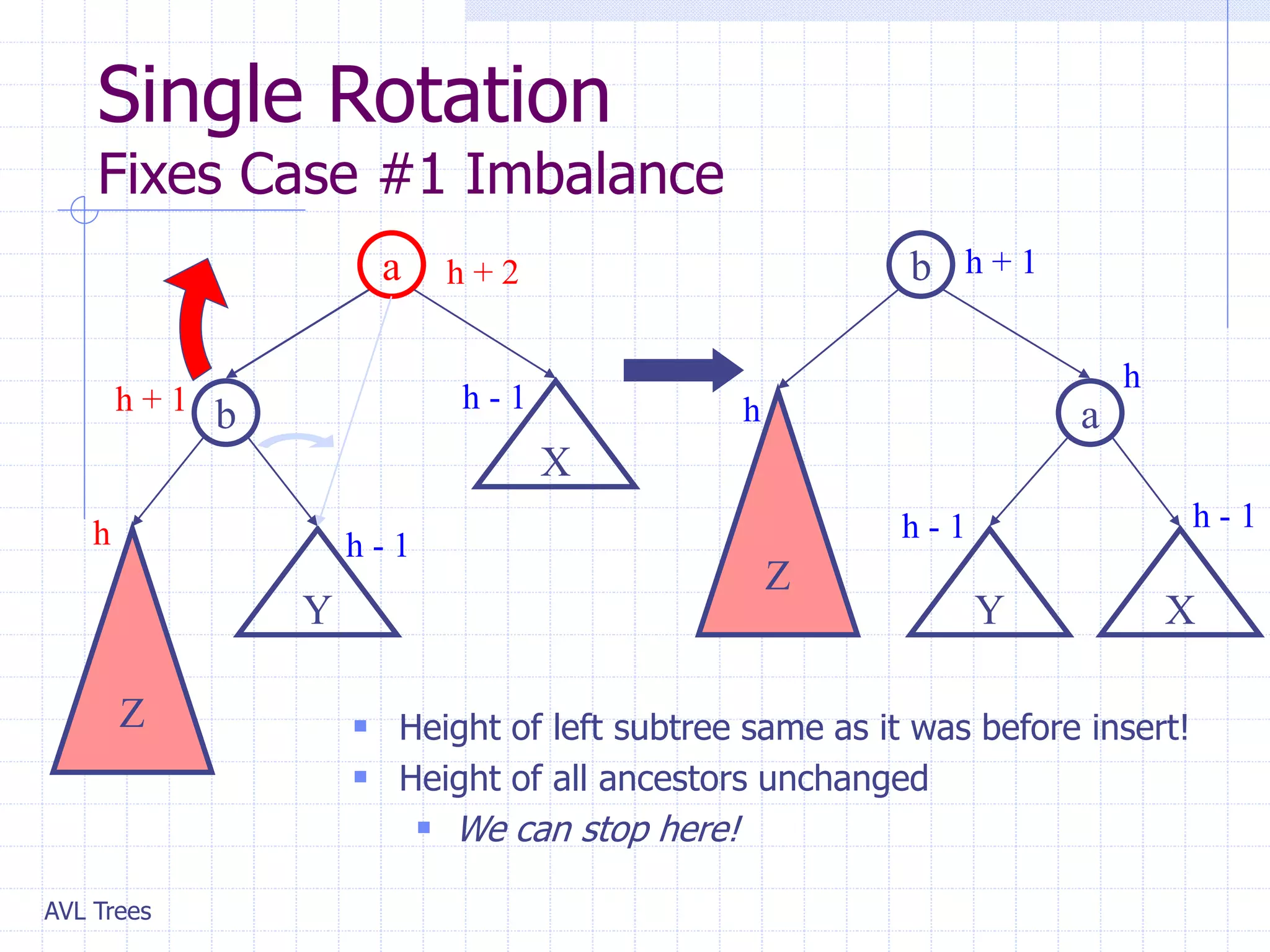
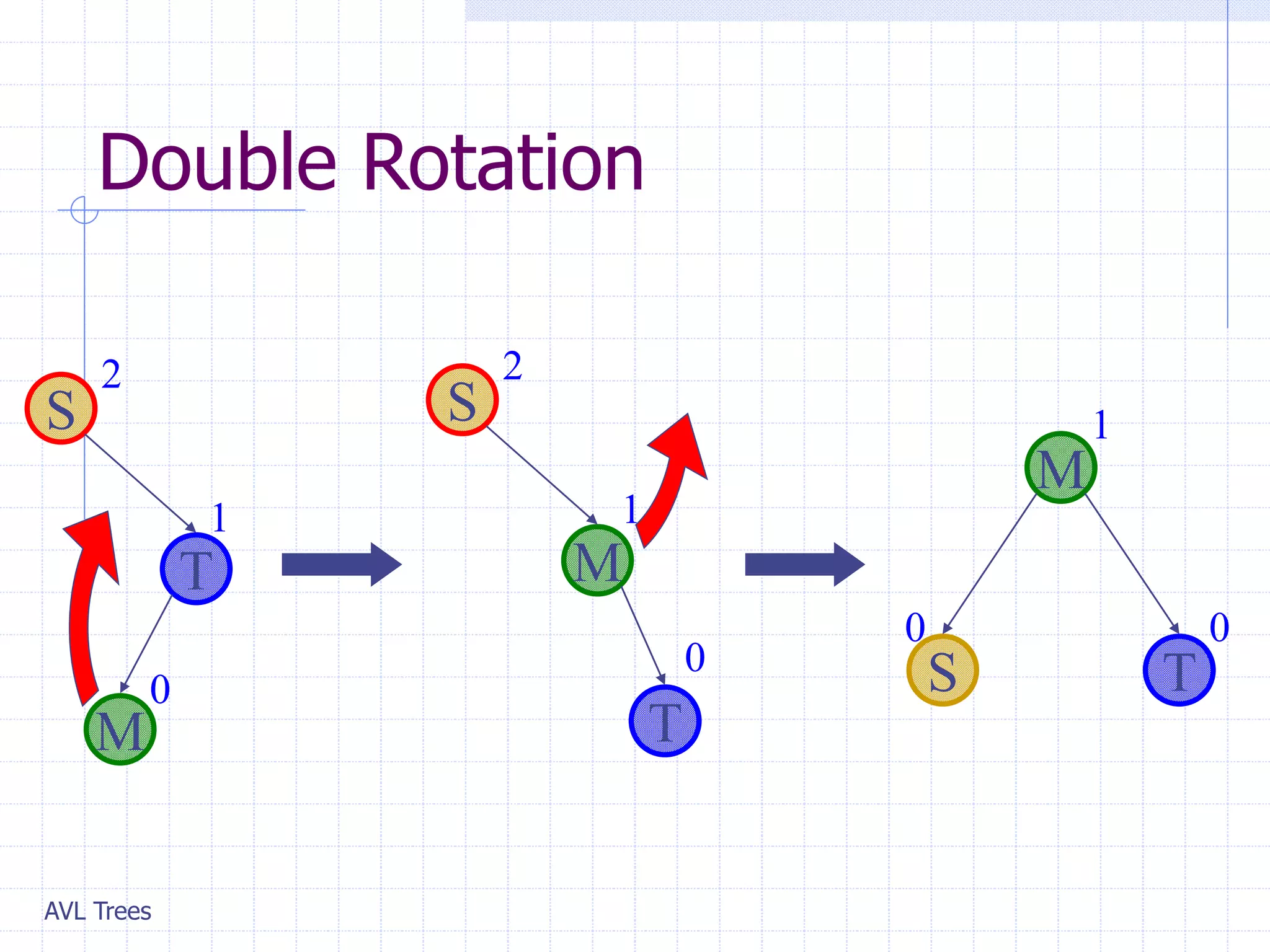
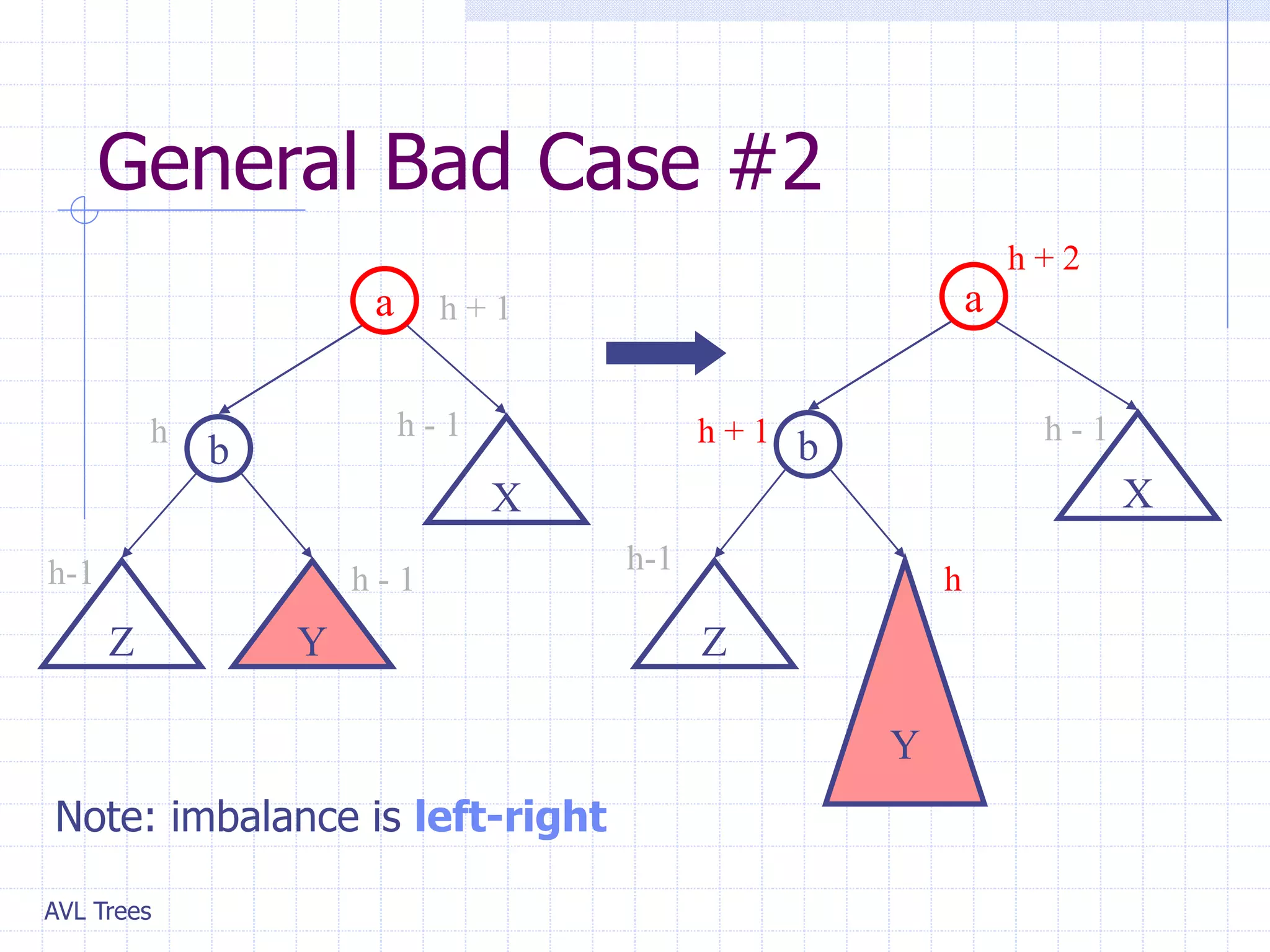
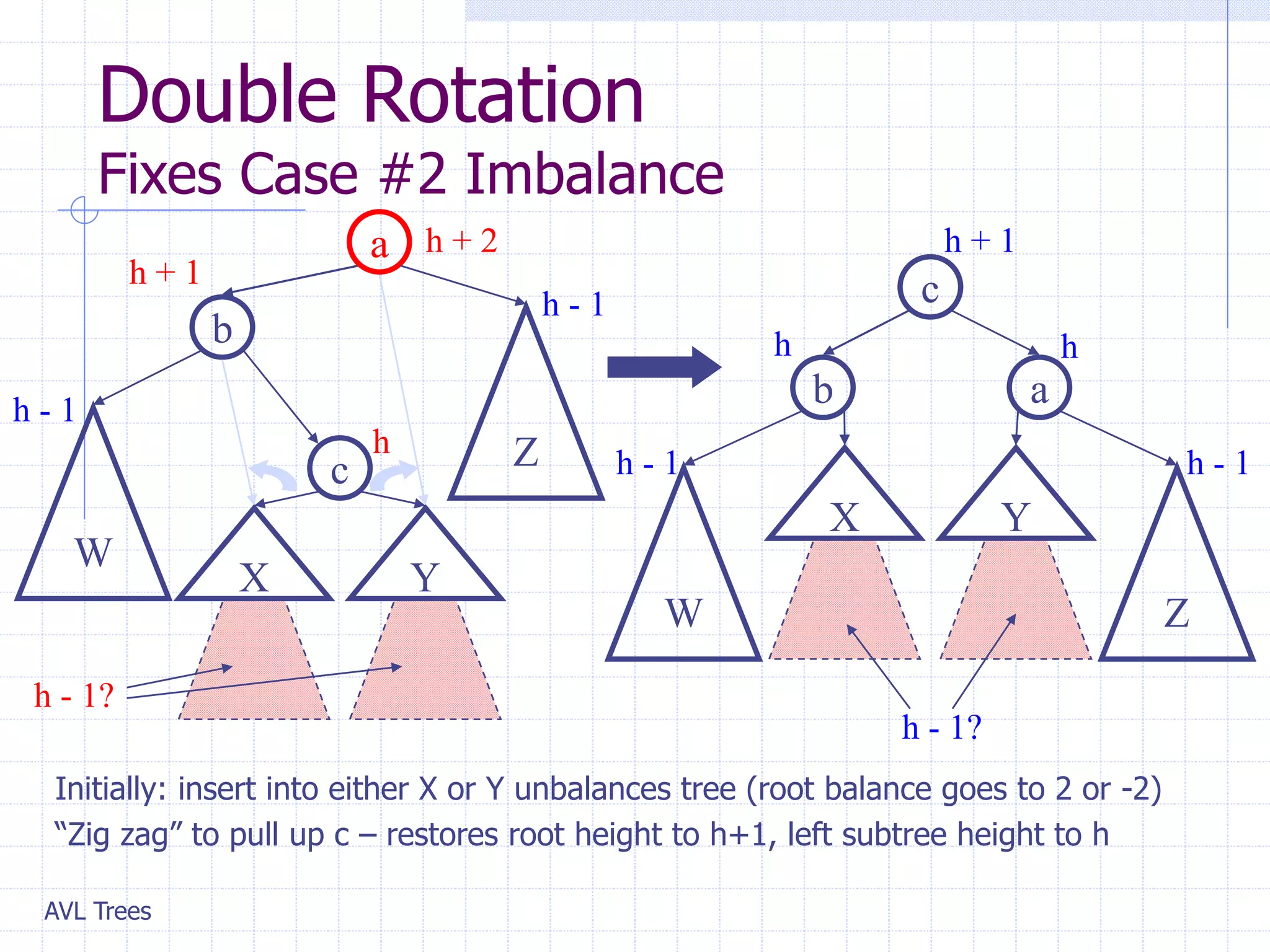
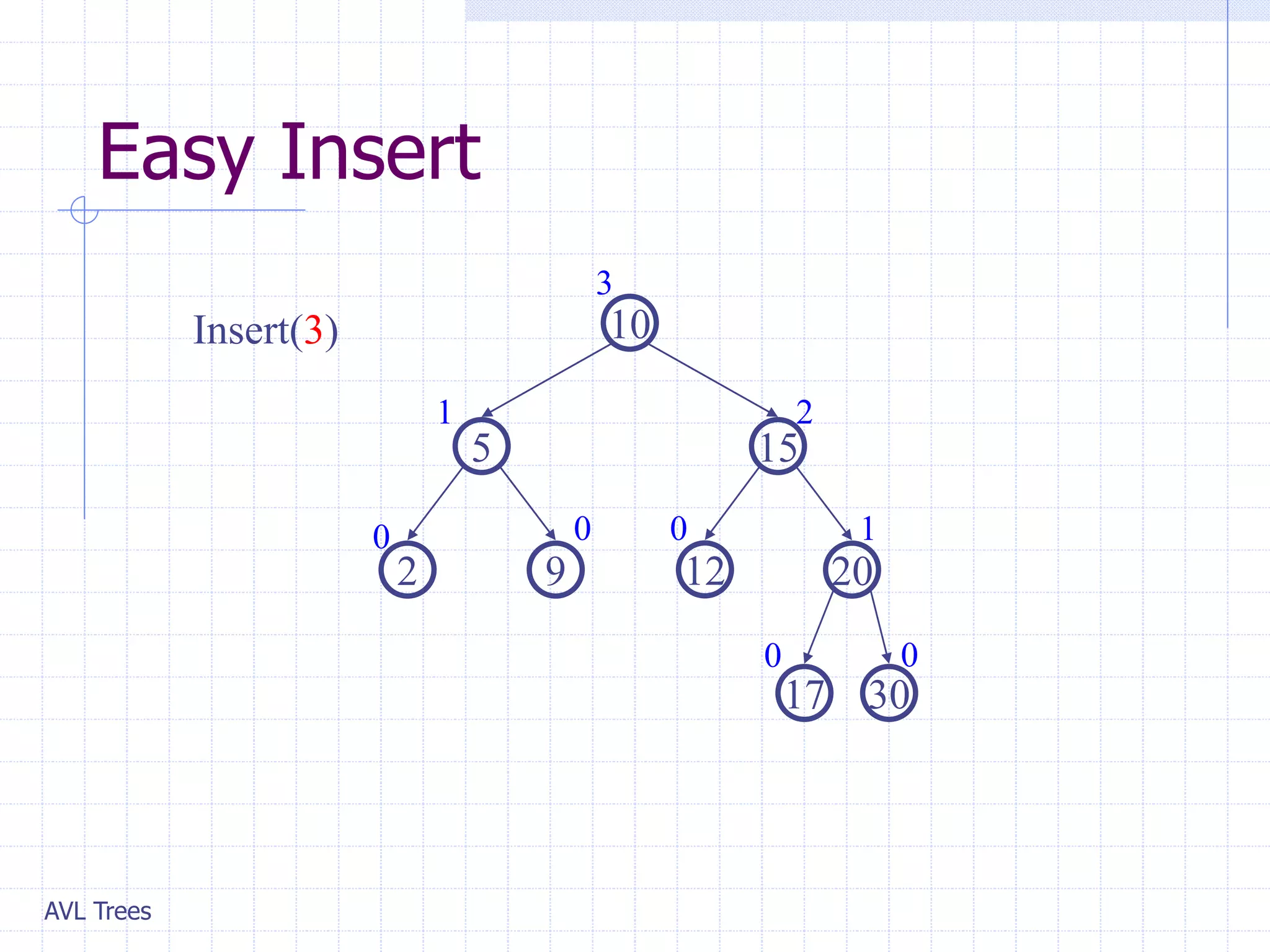
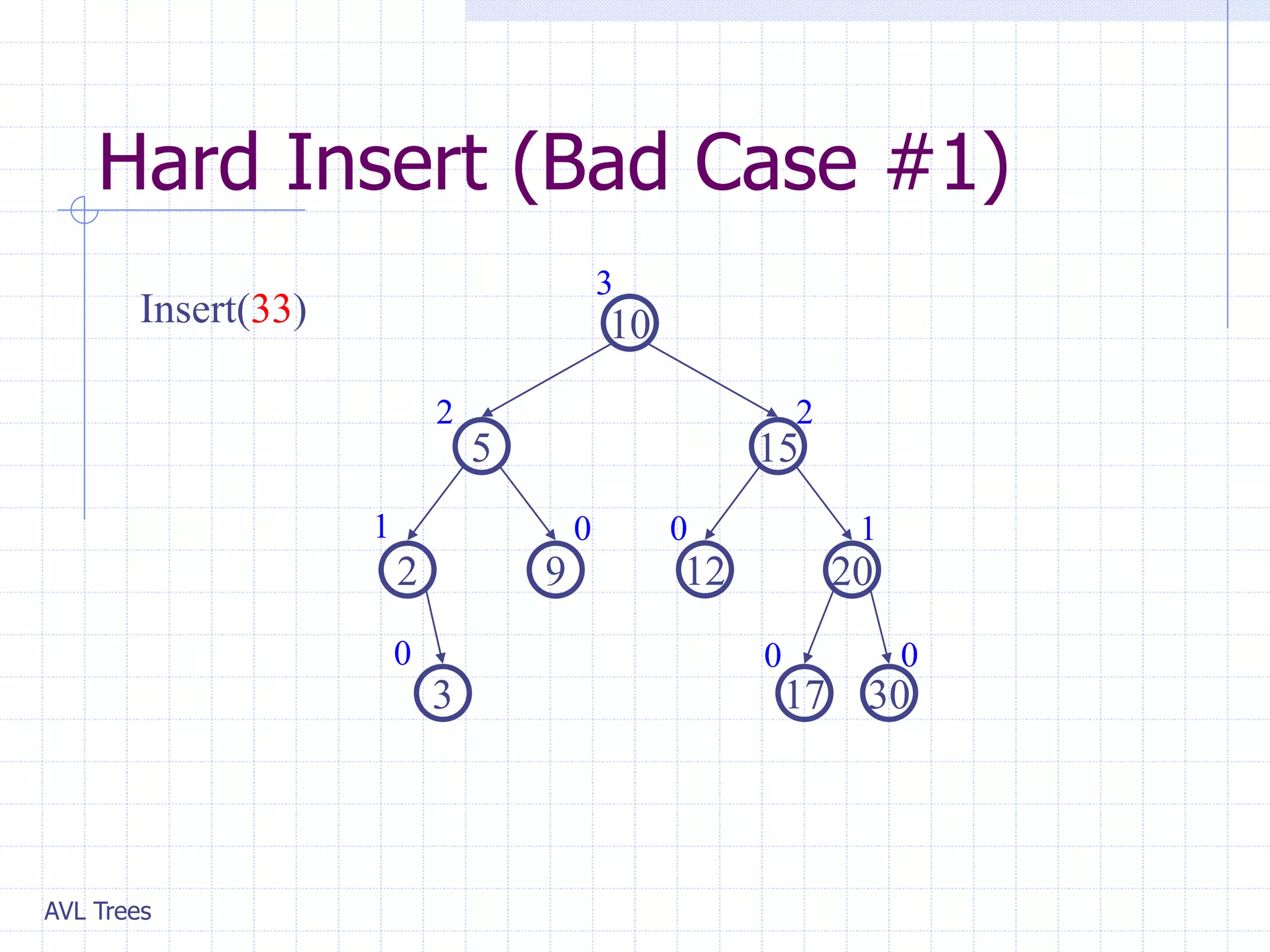
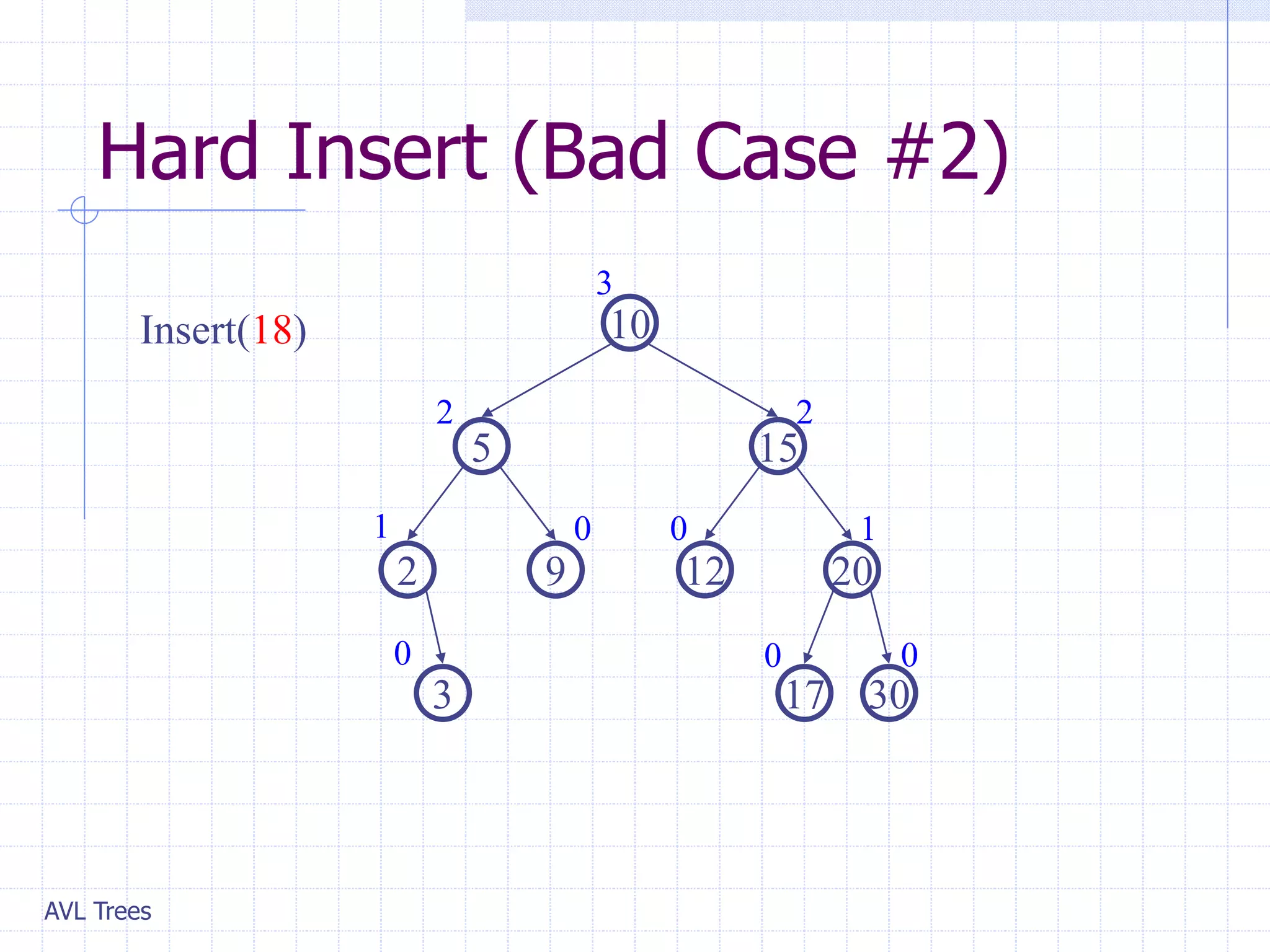
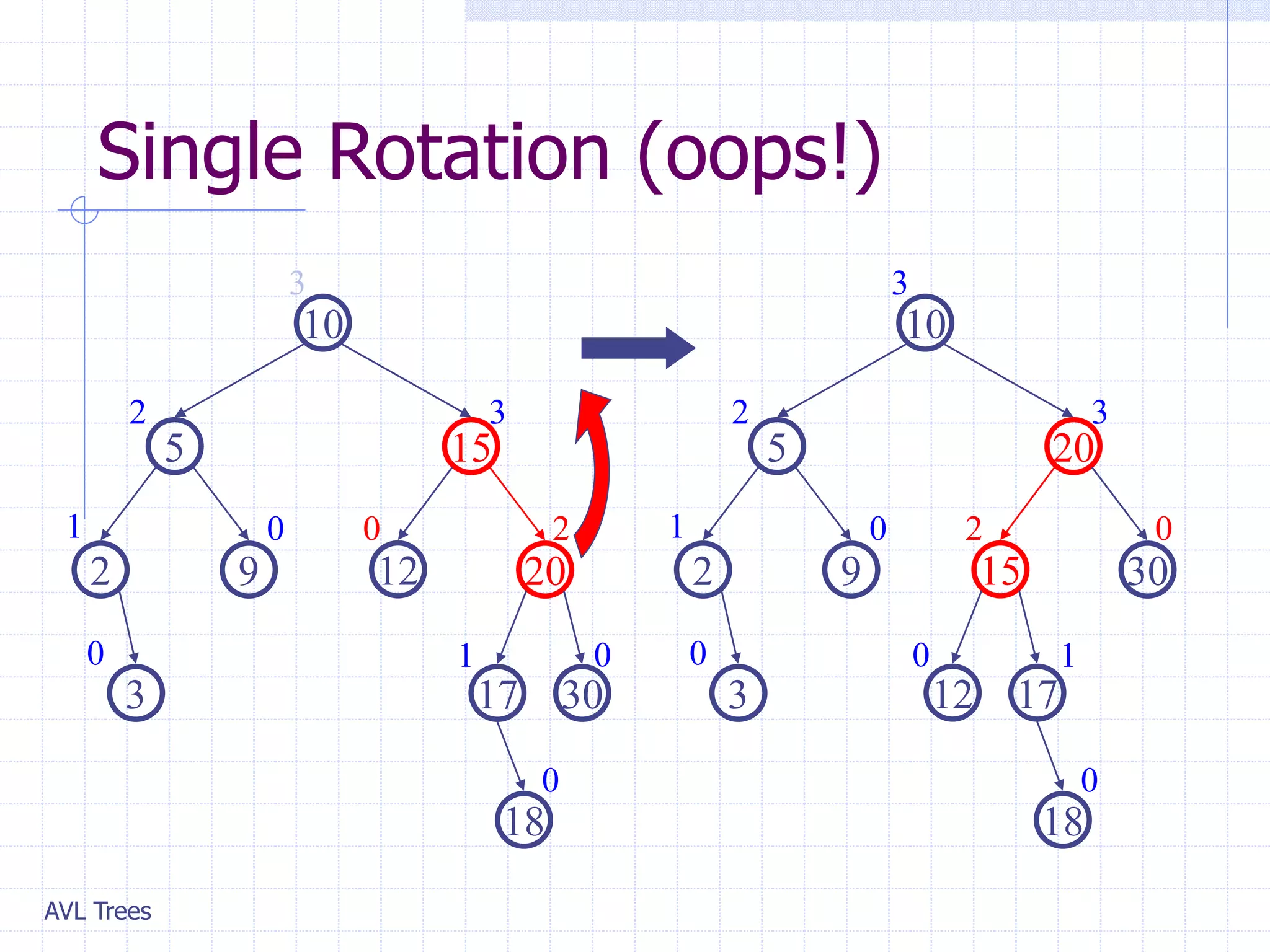
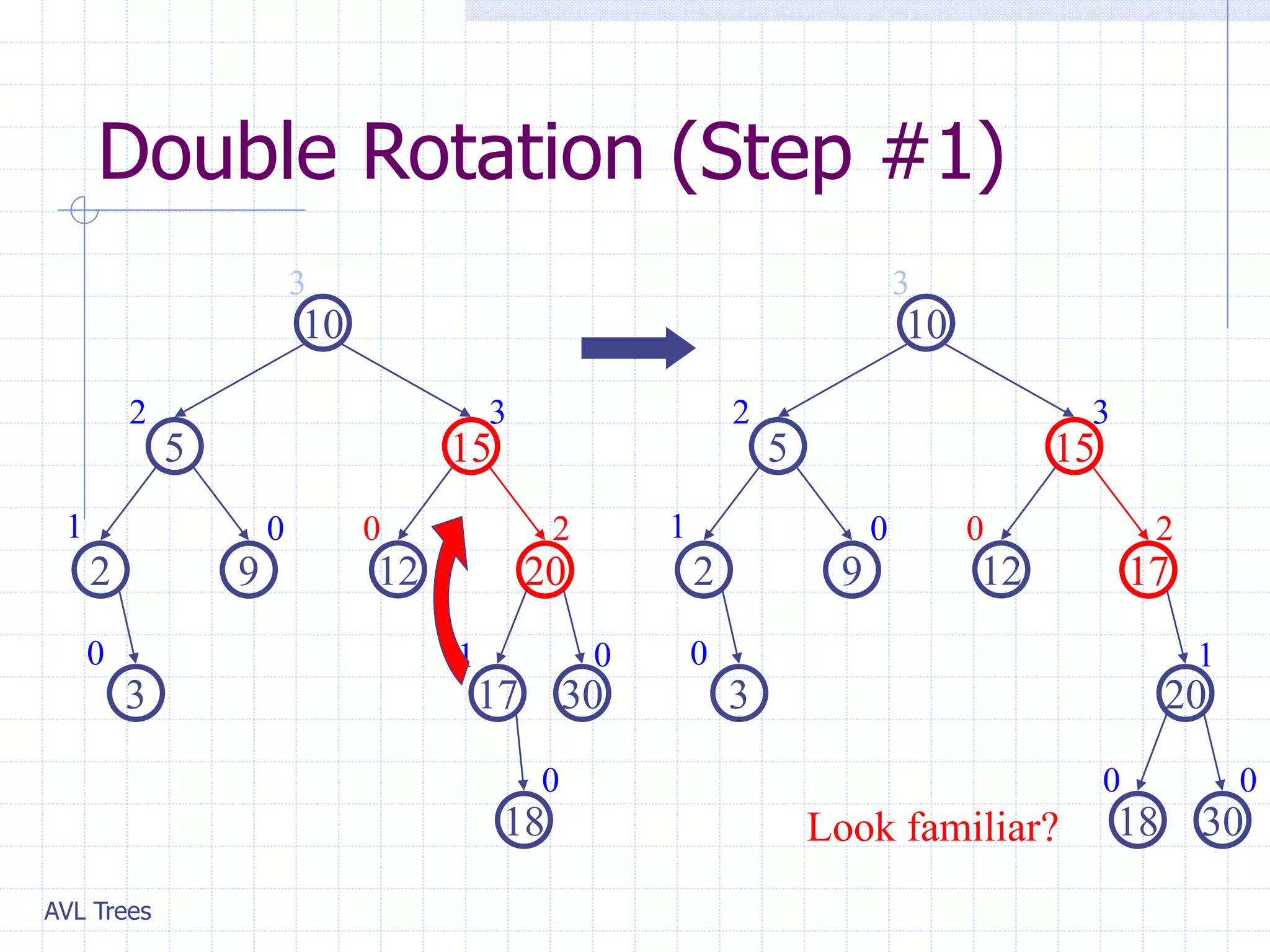
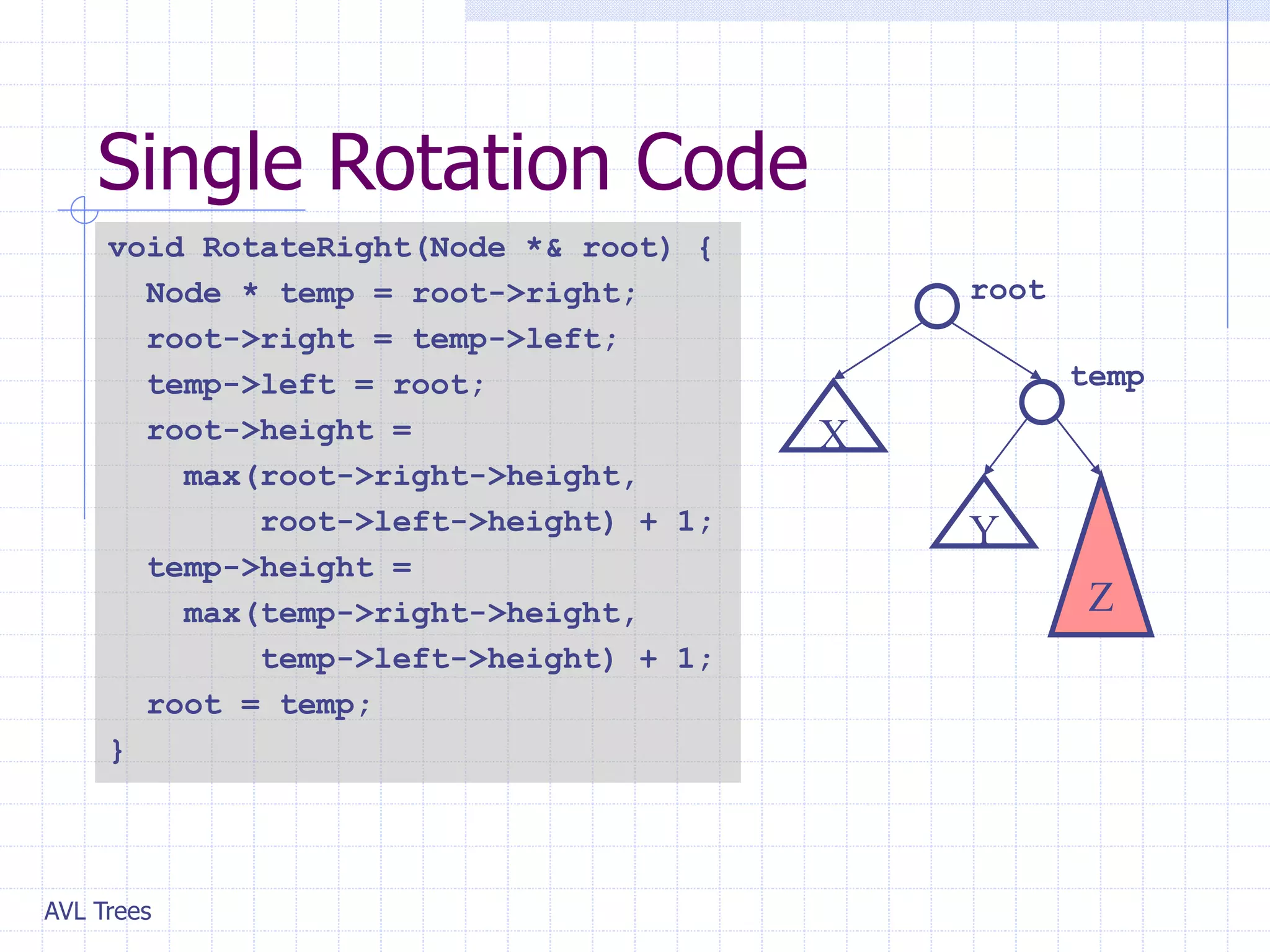
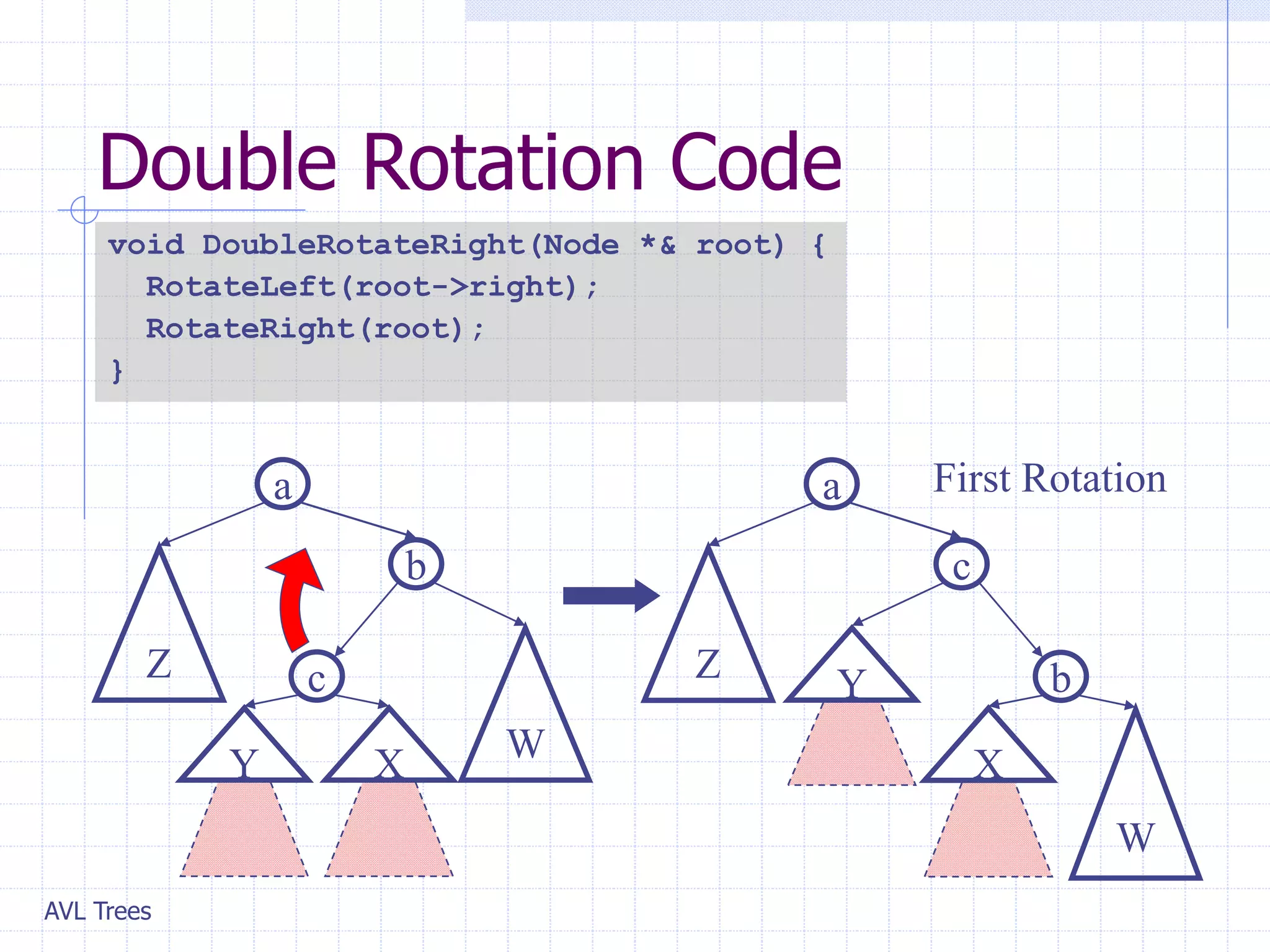
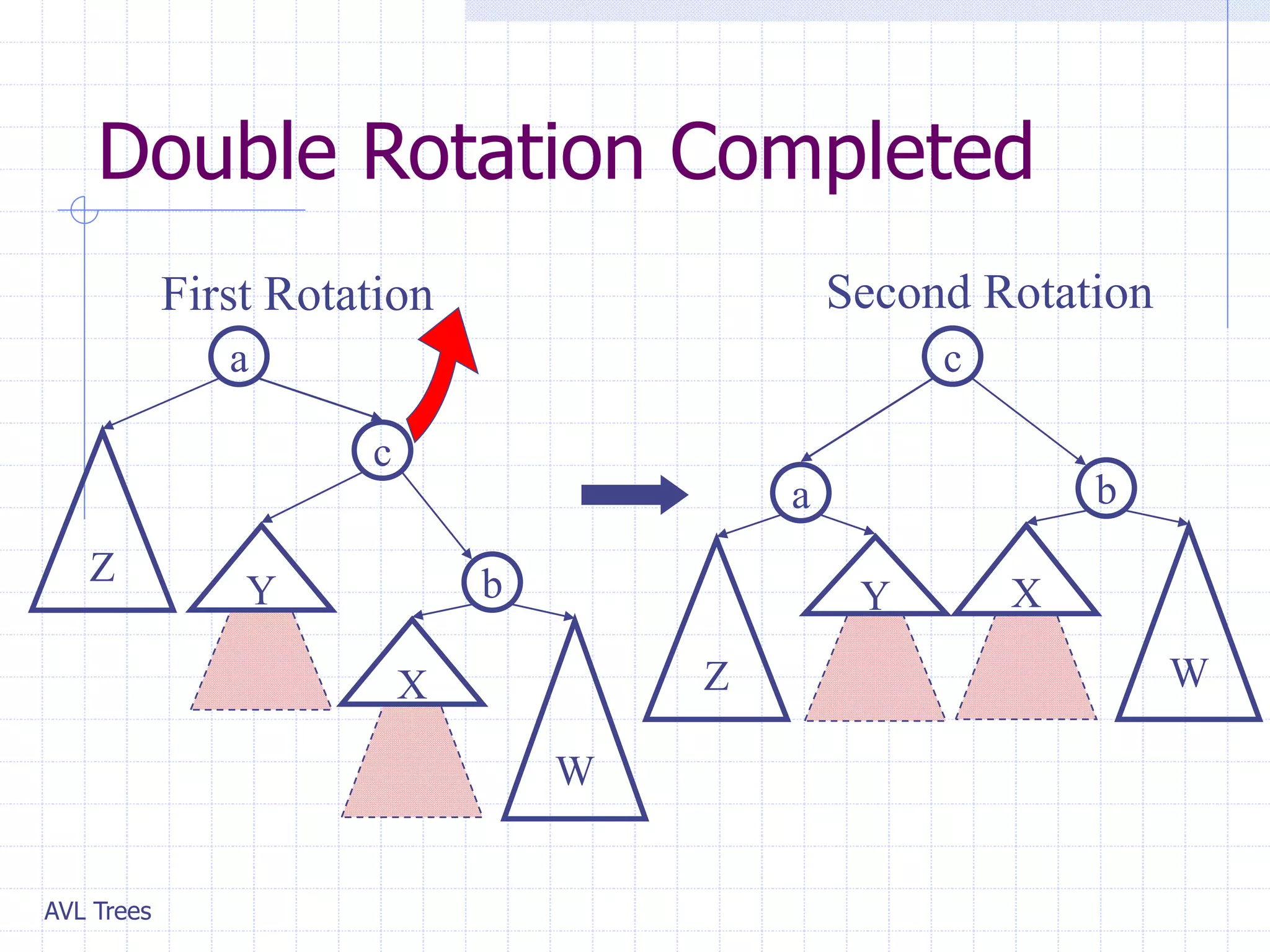
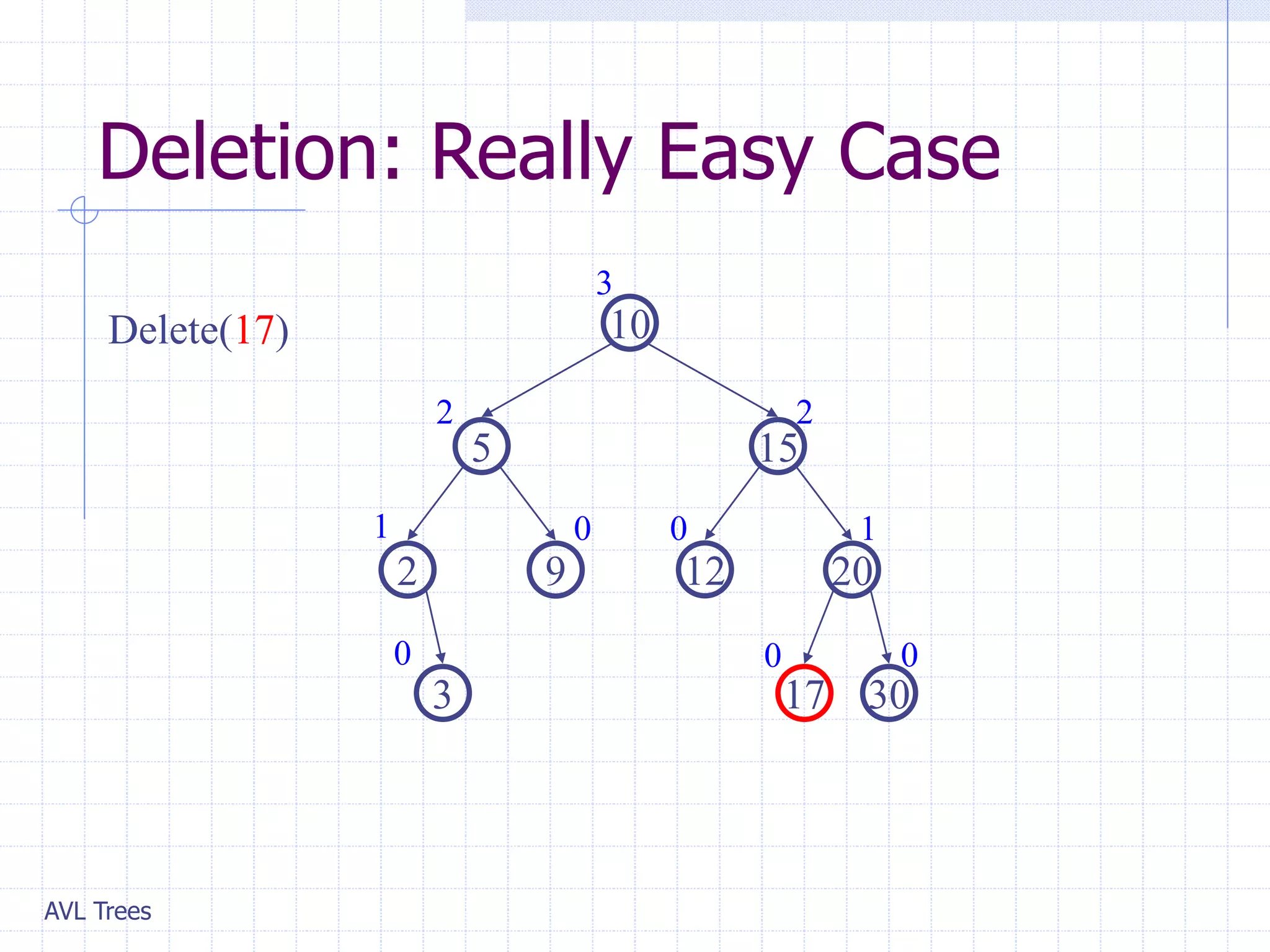
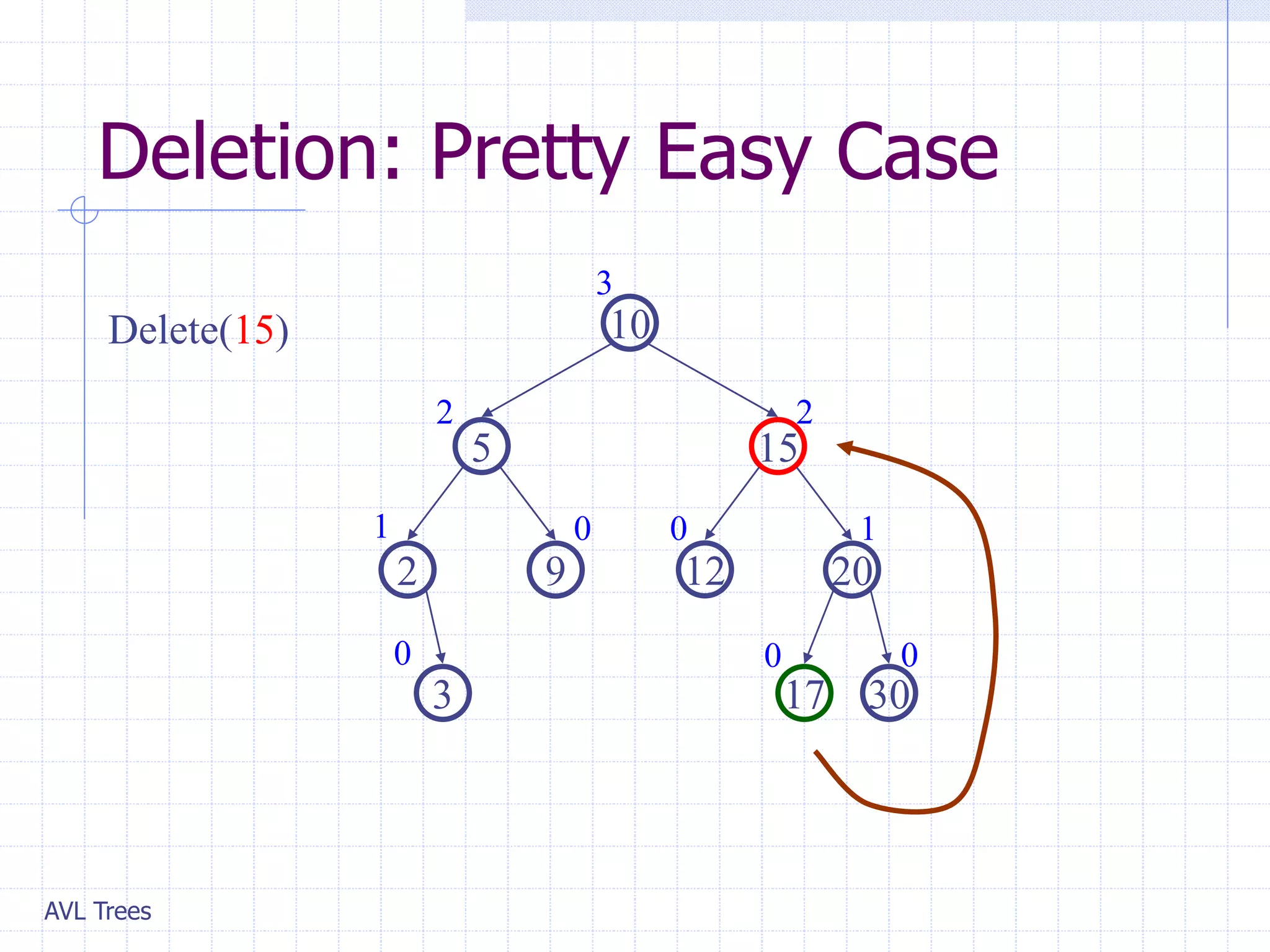
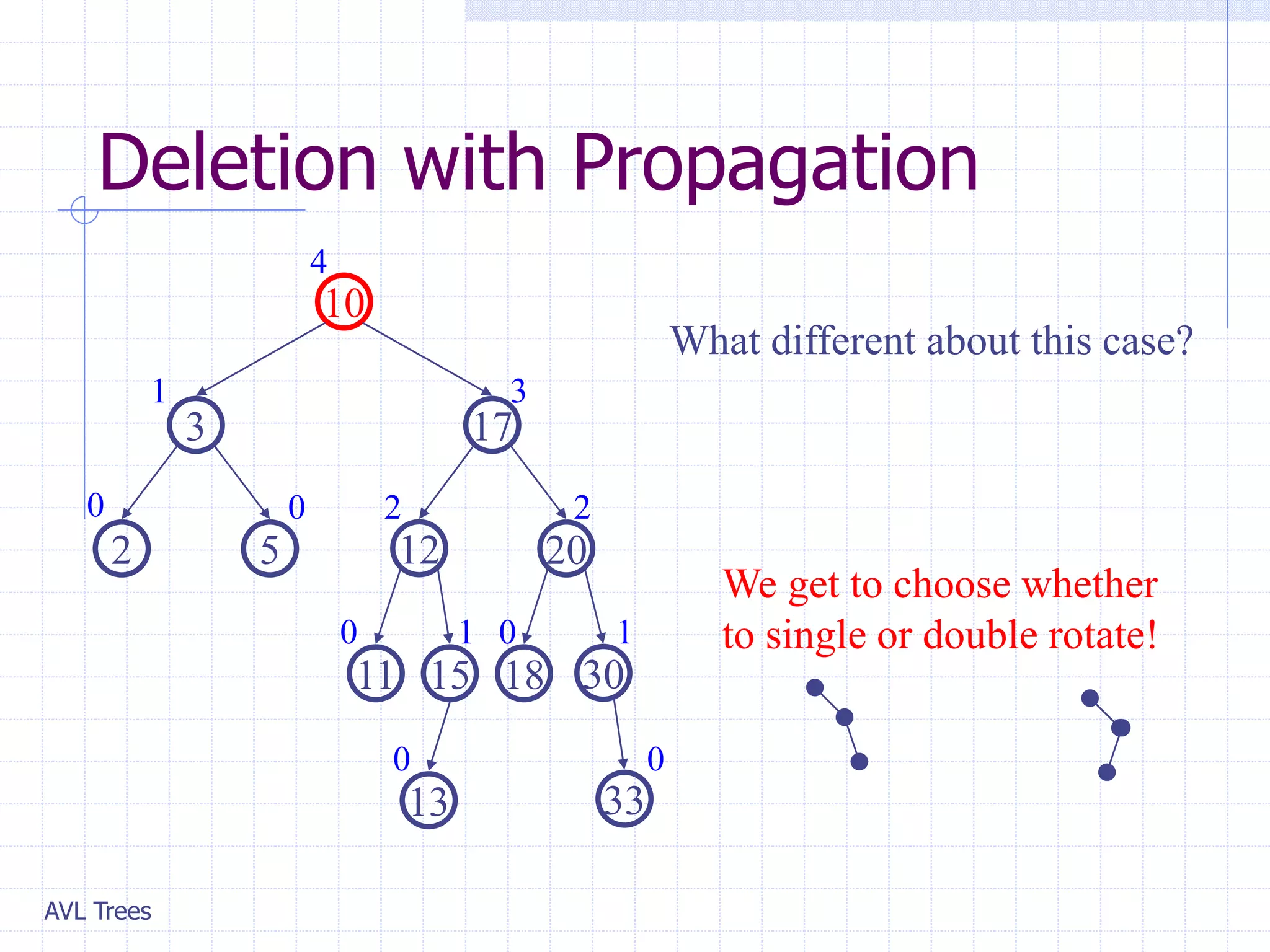
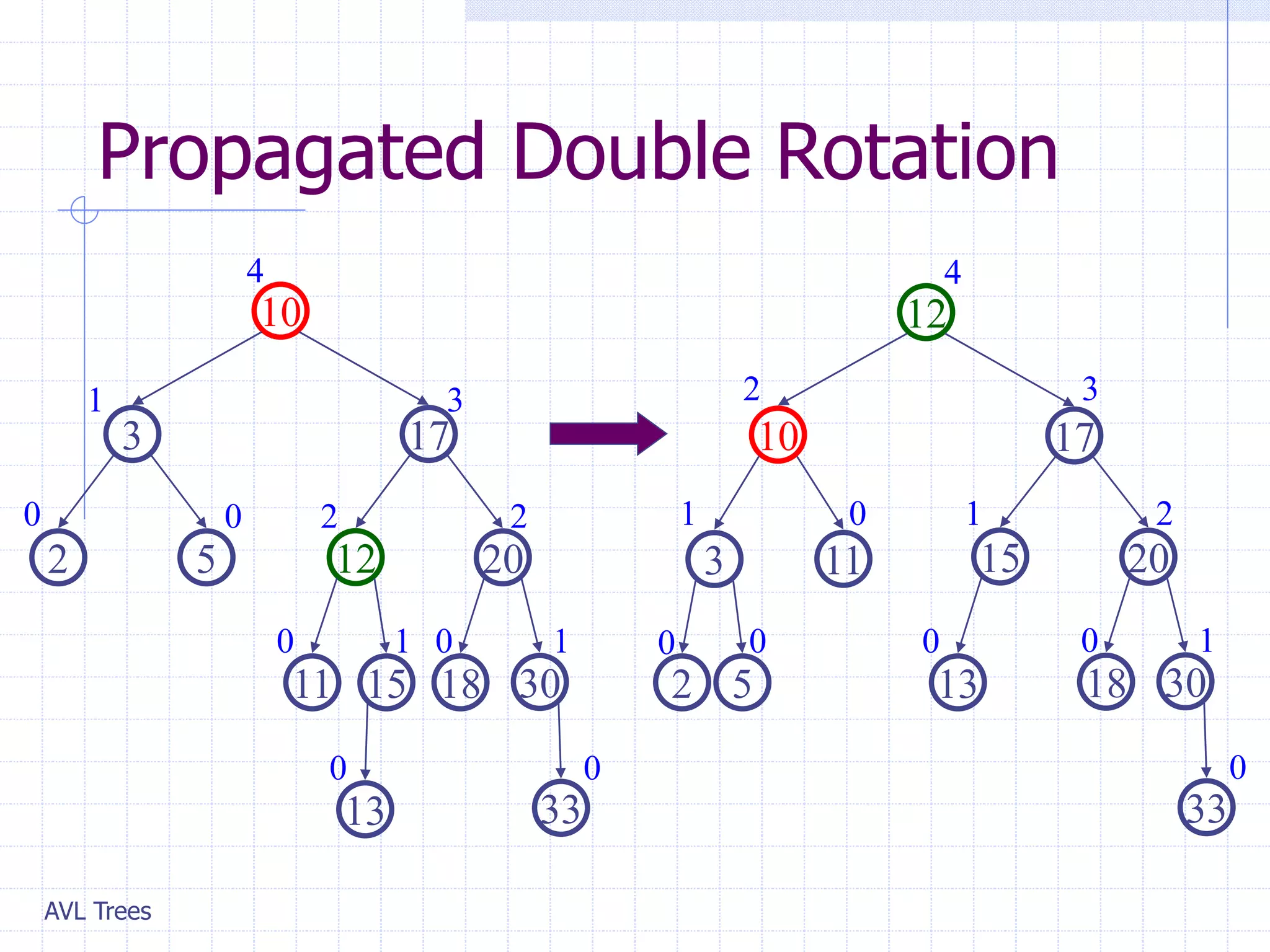
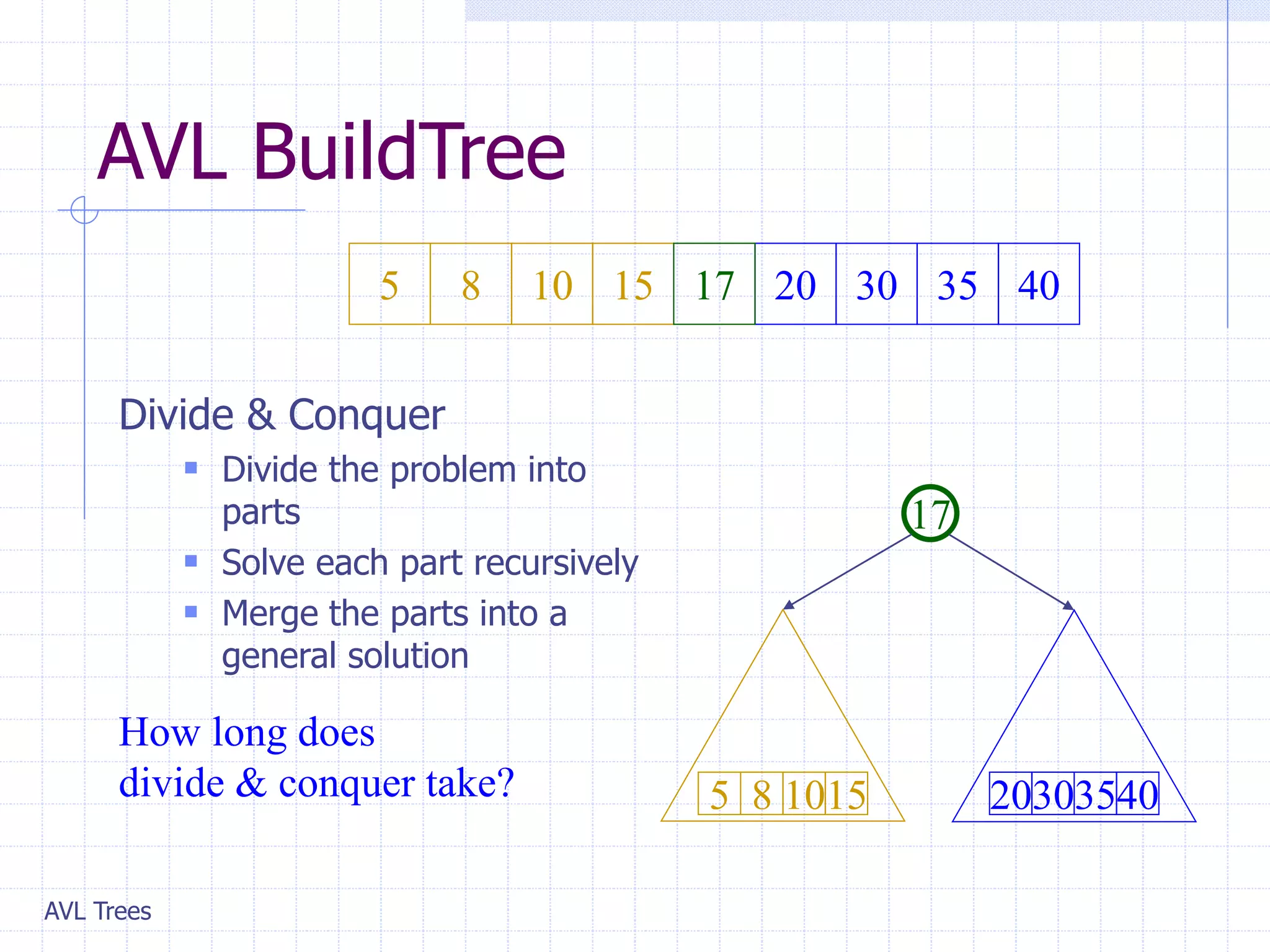
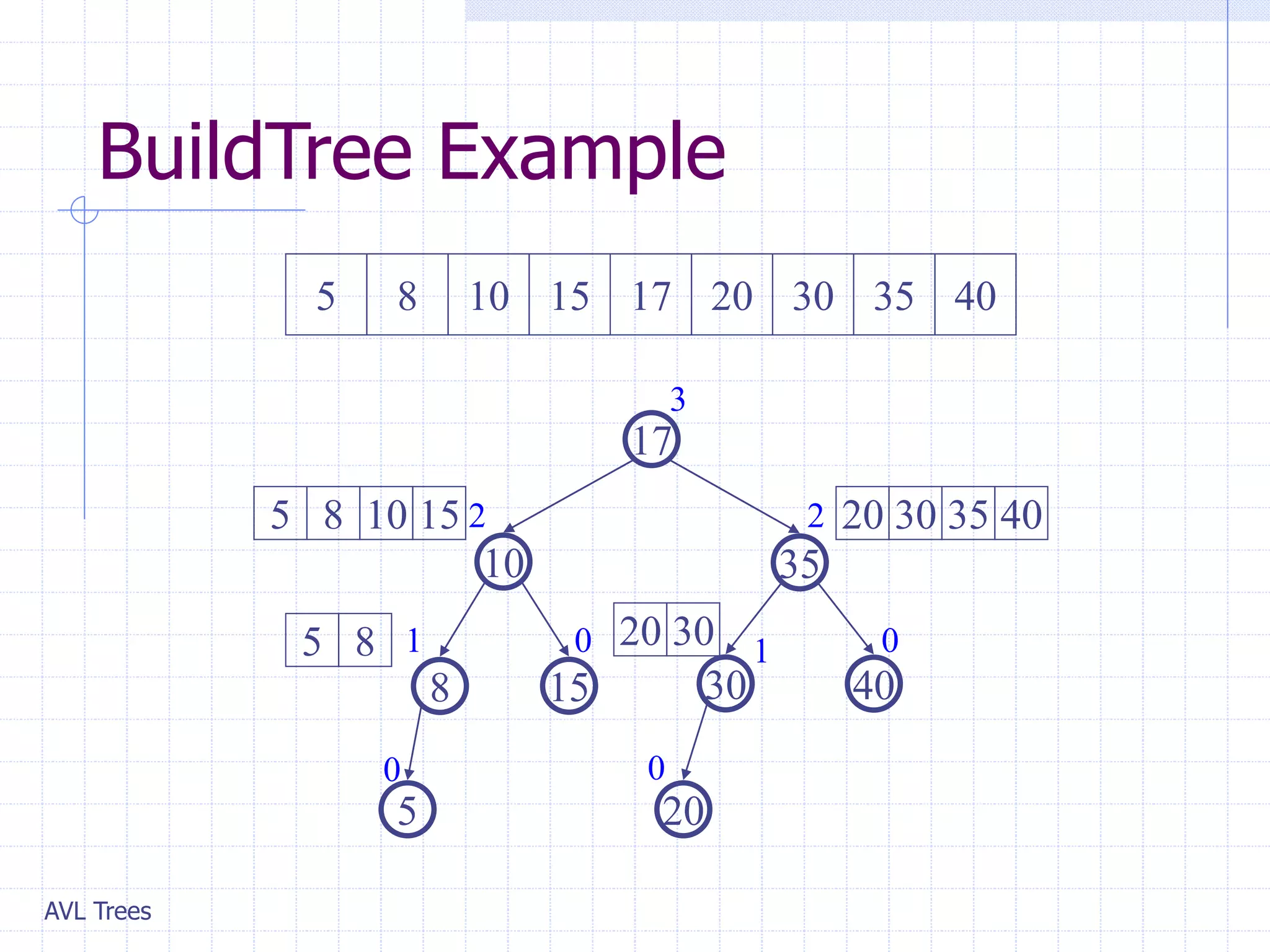
This document provides an overview of AVL Trees. It discusses that AVL Trees are self-balancing binary search trees that ensure the heights of the two child subtrees of any node differ by at most one. This balancing property guarantees search, insertion, and deletion operations will take O(log n) time in the worst case. The document covers the concepts of balance factors, single and double rotations used to rebalance the tree during insertions and deletions, and provides pseudocode for the AVL tree insertion and deletion algorithms. It also analyzes the O(n) time complexity of building an AVL tree from a sorted array.

1. AVL Trees
AVL Trees

2. AVL Trees
Balance
Balance == height(left subtree) - height(right subtree)
 zero everywhere  perfectly balanced
 small everywhere  balanced enough
Balance between -1 and 1 everywhere
 maximum height of ~1.44 log n
t
5
7

3. AVL Trees
AVL Tree
Dictionary Data Structure
4
12
10
6
2
11
5
8
14
13
7 9
Binary search tree properties
 binary tree property
 search tree property
Balance property
 balance of every node is:
-1 b  1
 result:
 depth is (log n)
15

4. AVL Trees
An AVL Tree
15
9
2 12
5
10
20
17
0
0
1
0
0
1 2
3 10
3
data
height
children
30
0

5. AVL Trees
Not AVL Trees
15
12
5
10
20
17
0
1
0
0 2
3
30
0
15
10
20
0
1
2 (-1)-1 = -2
0-2 = -2
Note: height(empty tree) == -1

6. AVL Trees
Good Insert Case:
Balance Preserved
Good case: insert middle, then small,then tall
Insert(middle)
Insert(small)
Insert(tall)
M
S T
0
0
1

7. AVL Trees
Bad Insert Case #1:
Left-Left or Right-Right Imbalance
Insert(small)
Insert(middle)
Insert(tall)
T
M
S
0
1
2
BC#1 Imbalance caused by either:
 Insert into left child’s left subtree
 Insert into right child’s right subtree

8. AVL Trees
Single Rotation
T
M
S
0
1
2
M
S T
0
0
1
Basic operation used in AVL trees:
A right child could legally have its parent as its left child.

9. AVL Trees
General Bad Case #1
a
X
Y
b
Z
h h - 1
h + 1 h - 1
h + 2
a
X
Y
b
Z
h-1 h - 1
h h - 1
h + 1
Note: imbalance is left-left

10. AVL Trees
Single Rotation
Fixes Case #1 Imbalance
 Height of left subtree same as it was before insert!
 Height of all ancestors unchanged
 We can stop here!
a
X
Y
b
Z
a
X
Y
b
Z
h h - 1
h + 1 h - 1
h + 2
h
h - 1
h
h - 1
h + 1

11. AVL Trees
Bad Insert Case #2:
Left-Right or Right-Left Imbalance
Insert(small)
Insert(tall)
Insert(middle)
M
T
S
0
1
2
Will a single rotation fix this?
BC#2 Imbalance caused by either:
 Insert into left child’s right subtree
 Insert into right child’s left subtree

12. AVL Trees
Double Rotation
M
S T
0
0
1
M
T
S
0
1
2
T
M
S
0
1
2

13. AVL Trees
General Bad Case #2
a
X
b
Z
h
h + 1 h - 1
h + 2
a
X
b
Z
h-1 h - 1
h h - 1
h + 1
Note: imbalance is left-right
h-1
Y
Y

14. AVL Trees
Double Rotation
Fixes Case #2 Imbalance
Initially: insert into either X or Y unbalances tree (root balance goes to 2 or -2)
“Zig zag” to pull up c – restores root height to h+1, left subtree height to h
a
Z
b
W
c
X Y
a
Z
b
W
c
X Y
h
h - 1?
h - 1
h - 1
h + 2
h + 1
h - 1
h - 1
h
h + 1
h
h - 1?

15. AVL Trees
AVL Insert Algorithm
 Find spot for value
 Hang new node
 Search back up looking for imbalance
 If there is an imbalance:
case #1: Perform single rotation
case #2: Perform double rotation
 Done!
(There can only be one imbalance!)

16. AVL Trees
Easy Insert
20
9
2
15
5
10
30
17
Insert(3)
12
0
0
1
0
0
1 2
3
0

17. AVL Trees
Hard Insert (Bad Case #1)
20
9
2
15
5
10
30
17
Insert(33)
3
12
1
0
1
0
0
2 2
3
0
0

18. AVL Trees
Single Rotation
20
9
2
15
5
10
30
17
3
12
33
1
0
2
0
0
2 3
3
1
0
0
30
9
2
20
5
10
33
3
15
1
0
1
1
0
2 2
3
0
0
17
12
0

19. AVL Trees
Hard Insert (Bad Case #2)
Insert(18)
20
9
2
15
5
10
30
17
3
12
1
0
1
0
0
2 2
3
0
0

20. AVL Trees
Single Rotation (oops!)
20
9
2
15
5
10
30
17
3
12
1
1
2
0
0
2 3
3
0
0
30
9
2
20
5
10
3
15
1
1
0
2
0
2 3
3
0
17
12
0
18
0
18
0

21. AVL Trees
Double Rotation (Step #1)
20
9
2
15
5
10
30
17
3
12
1
1
2
0
0
2 3
3
0
0
18
0
17
9
2
15
5
10
20
3
12
1 2
0
0
2 3
3
1
0
30
0
Look familiar? 18
0

22. AVL Trees
Double Rotation (Step #2)
17
9
2
15
5
10
20
3
12
1 2
0
0
2 3
3
1
0
30
0
18
0
20
9
2
17
5
10
30
3
15
1
0
1
1
0
2 2
3
0
0
12
0
18

23. AVL Trees
AVL Insert Algorithm Revisited
 Recursive
1. Search downward for
spot
2. Insert node
3. Unwind stack,
correcting heights
a. If imbalance #1,
single rotate
b. If imbalance #2,
double rotate
 Iterative
1. Search downward for
spot, stacking
parent nodes
2. Insert node
3. Unwind stack,
correcting heights
a. If imbalance #1,
single rotate and
exit
b. If imbalance #2,
double rotate and
exit

24. AVL Trees
Single Rotation Code
void RotateRight(Node *& root) {
Node * temp = root->right;
root->right = temp->left;
temp->left = root;
root->height =
max(root->right->height,
root->left->height) + 1;
temp->height =
max(temp->right->height,
temp->left->height) + 1;
root = temp;
}
X
Y
Z
root
temp

25. AVL Trees
Double Rotation Code
void DoubleRotateRight(Node *& root) {
RotateLeft(root->right);
RotateRight(root);
}
a
Z
b
W
c
X
Y
a
Z
c
b
X
Y
W
First Rotation

26. AVL Trees
Double Rotation Completed
a
Z
c
b
X
Y
W
a
Z
c
b
X
Y
W
First Rotation Second Rotation

27. AVL Trees
Deletion: Really Easy Case
20
9
2
15
5
10
30
17
3
12
1
0
1
0
0
2 2
3
0
0
Delete(17)

28. AVL Trees
Deletion: Pretty Easy Case
20
9
2
15
5
10
30
17
3
12
1
0
1
0
0
2 2
3
0
0
Delete(15)

29. AVL Trees
Deletion: Pretty Easy Case (cont.)
20
9
2
17
5
10
30
3
12
1 1
0
0
2 2
3
0
0
Delete(15)

30. AVL Trees
Deletion (Hard Case #1)
20
9
2
17
5
10
30
3
12
1 1
0
0
2 2
3
0
0
Delete(12)

31. AVL Trees
Single Rotation on Deletion
20
9
2
17
5
10
30
3
1 1
0
2 2
3
0
0
30
9
2
20
5
10
17
3
1 0
0
2 1
3
0
0
Deletion can differ from insertion – How?

32. AVL Trees
Deletion (Hard Case)
Delete(9)
20
9
2
17
5
10
30
3
12
1 2
2
0
2 3
4
0
33
15
13
0 0
1
0
20
30
12
33
15
13
1
0 0
11
0
18
0

33. AVL Trees
Double Rotation on Deletion
2
3
0
20
2
17
5
10
30
12
1 2
2
2 3
4
33
15
13
1
0 0
1
11
0
18
0
20
5
2
17
3
10
30
12
0 2
2
0
1 3
4
33
15
13
1
0 0
1
11
0
18
0
0
Not
finished!

34. AVL Trees
Deletion with Propagation
We get to choose whether
to single or double rotate!
20
5
2
17
3
10
30
12
0 2
2
0
1 3
4
33
15
13
1
0 0
1
11
0
18
0
What different about this case?

35. AVL Trees
Propagated Single Rotation
0
30
20
17
33
12
15
13
1
0
5
2
3
10
4
3 2
1 2 1
0 0 0
11
0
20
5
2
17
3
10
30
12
0 2
2
0
1 3
4
33
15
13
1
0
1
11
0
18
0
18
0

36. AVL Trees
Propagated Double Rotation
0
17
12
11
5
2
3
10
4
2 3
1 0
0 0
20
5
2
17
3
10
30
12
0 2
2
0
1 3
4
33
15
13
1
0
1
11
0
18
0
15
1
0
20
30
33
1
18
0
13
0
2

37. AVL Trees
AVL Deletion Algorithm
 Recursive
1. Search downward for
node
2. Delete node
3. Unwind, correcting
heights as we go
a. If imbalance #1,
single rotate
b. If imbalance #2
(or don’t care),
double rotate
 Iterative
1. Search downward for
node, stacking
parent nodes
2. Delete node
3. Unwind stack,
correcting heights
a. If imbalance #1,
single rotate
b. If imbalance #2
(or don’t care)
double rotate

38. AVL Trees
Building an AVL Tree
Input: sequence of n keys (unordered)
19 3 4 18 7
Insert each into initially empty AVL tree
But, suppose input is already sorted …
3 4 7 18 19
Can we do better than O(n log n)?
1 1
( lo
l g )
og log
n n
i i
O n n
i n
 
 
 

39. AVL Trees
AVL BuildTree
8 10 15 20 30 35 40
5
17
17
8 1015
5 20303540
Divide & Conquer
 Divide the problem into
parts
 Solve each part recursively
 Merge the parts into a
general solution
How long does
divide & conquer take?

40. AVL Trees
BuildTree Example
35
17
15
5
8
10
3
2 2
1 0
0
30
1
40
20
0
0
8 10 15 20 30 35 40
5 17
8 10 15
5
8
5
30 35 40
20
30
20

41. AVL Trees
BuildTree Analysis
(Approximate)
T(1) = 1
T(n) = 2T(n/2) + 1
T(n) = 2(2T(n/4)+1) + 1
T(n) = 4T(n/4) + 2 + 1
T(n) = 4(2T(n/8)+1) + 2 + 1
T(n) = 8T(n/8) + 4 + 2 + 1
T(n) = 2kT(n/2k) +
let 2k = n, log n = k
T(n) = nT(1) +
T(n) = (n)


k
i
i
1
2
2
1


n
i
i
log
1
2
2
1

42. AVL Trees
Precise Analysis: T(0) = b
T(n) = T( ) + T( ) + c
By induction on n:
T(n) = (b+c)n + b
Base case:
T(0) = b = (b+c)0 + b
Induction step:
T(n) = (b+c) + b +
(b+c) + b + c
= (b+c)n + b
QED: T(n) = (b+c)n + b = (n)





 
2
1
n





 
2
1
n





 
2
1
n





 
2
1
n
BuildTree Analysis
(Exact)
1
2
1
2
1







 






 
n
n
n

43. AVL Trees
Thinking About AVL
Observations
+ Worst case height of an AVL tree is about 1.44 log n
+ Insert, Find, Delete in worst case O(log n)
+ Only one (single or double) rotation needed on
insertion
+ Compatible with lazy deletion
- O(log n) rotations needed on deletion
- Height fields must be maintained (or 2-bit balance)
Coding complexity?

44. AVL Trees
Alternatives to AVL Trees
 Weight balanced trees
 keep about the same number of nodes in each subtree
 not nearly as nice
 Splay trees
 “blind” adjusting version of AVL trees
 no height information maintained!
 insert/find always rotates node to the root!
 worst case time is O(n)
 amortized time for all operations is O(log n)
 mysterious, but often faster than AVL trees in practice
(better low-order terms)