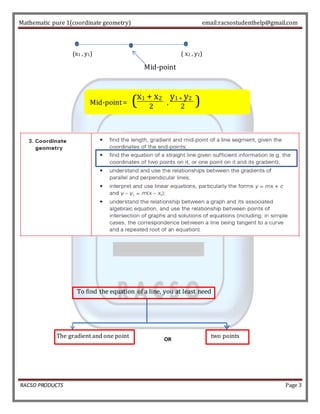
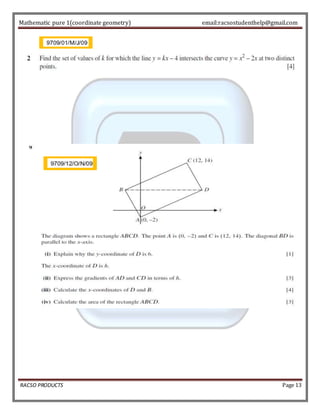
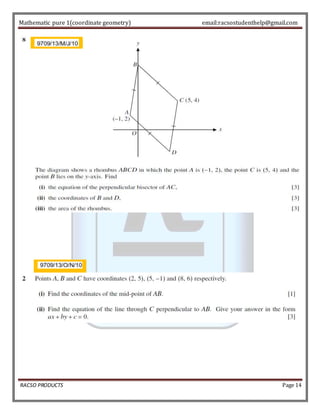
The document discusses key concepts in coordinate geometry, including:
- Length, gradient, and midpoint of lines between two points
- Finding the distance and equation of a line given two points or the gradient and one point
- Parallel and perpendicular lines having related gradients
- Finding the coordinates of points of intersection between two lines or a line and curve by solving their equations simultaneously
- Using the discriminant of a quadratic equation to determine the number of intersection points between a curve and line