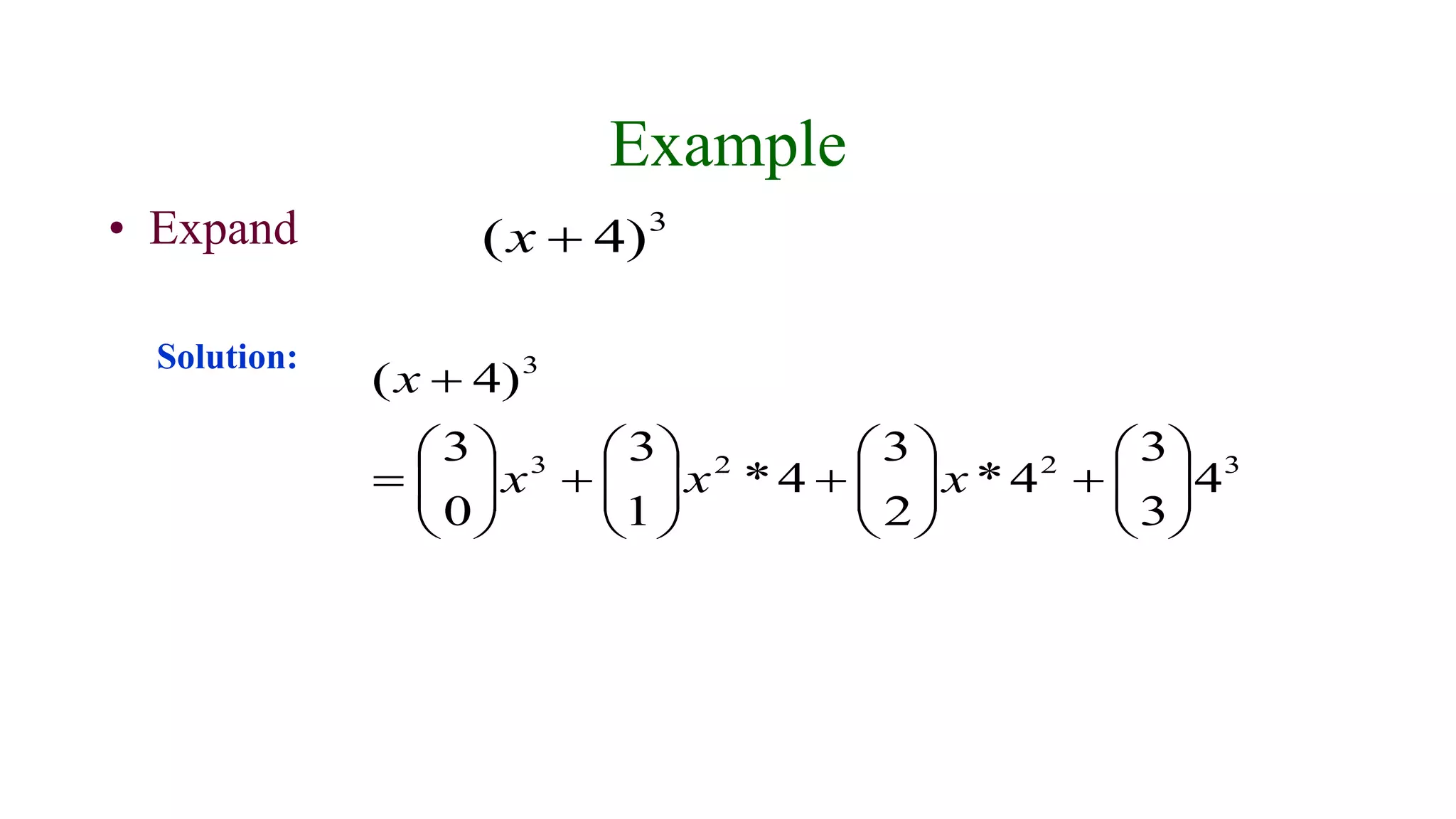The document discusses the binomial theorem, which provides a formula for expanding binomial expressions of the form (a + b)^n. It explains that the terms follow certain patterns, with the exponents of the variables alternating and summing to n. The coefficients of the terms form Pascal's triangle. The binomial theorem states that the expansion of (a + b)^n is the sum of terms with coefficients given by the binomial coefficients. Examples are provided to demonstrate expanding binomials and finding particular terms using the binomial theorem formula.

1. The Binomial Theorem

2. By studying the expanded form of each binomial expression, we are able to discover the following
patterns in the resulting polynomials.
1. The first term is an
. The exponent on a decreases by 1 in each successive term.
2. The exponents on b increase by 1 in each successive term. In the first term, the exponent on b is 0.
(Because b0
= 1, b is not shown in the first term.) The last term is bn
.
3. The sum of the exponents on the variables in any term is equal to n, the exponent on (a + b)n
.
4. There is one more term in the polynomial expansion than there is in the power of the binomial, n.
There are n + 1 terms in the expanded form of
(a + b)n
.
Using these observations, the variable parts of the expansion (a + b)6
are
a6
, a5
b, a4
b2
, a3
b3
, a2
b4
, ab5
, b6
.
Patterns in Binomial Expansions

3. Let's now establish a pattern for the coefficients of the terms in the binomial expansion. Notice that each
row in the figure begins and ends with 1. Any other number in the row can be obtained by adding the two
numbers immediately above it.
Coefficients for (a + b)1
.
Coefficients for (a + b)2
.
Coefficients for (a + b)3
.
Coefficients for (a + b)4
.
Coefficients for (a + b)5
.
Coefficients for (a + b)6
.
• 1
• 2 1
• 3 3 1
• 4 6 4 1
• 5 10 10 5 1
1 6 15 20 15 6 1
The above triangular array of coefficients is called Pascal’s triangle. We can use the numbers in the sixth
row and the variable parts we found to write the expansion for (a + b)6
. It is
(a + b)6
= a6
+ 6a5
b + 15a4
b2
+ 20a3
b3
+ 15a2
b4
+ 6ab5
+ b6
Patterns in Binomial Expansions

4. Definition of a Binomial
Coefficient
For nonnegative integers n and r, with
n > r, the expression is called a
binomial coefficient and is defined by








r
n








r
n
)!
(
!
!
r
n
r
n
r
n

=









5. Example








3
7
• Evaluate
Solution:
35
1
*
2
*
3
*
4
*
1
*
2
*
3
1
*
2
*
3
*
4
*
5
*
6
*
7
!
4
!
3
!
7
)!
3
7
(
!
3
!
7
3
7
)!
(
!
!
=
=
=

=









=








r
n
r
n
r
n

6. A Formula for Expanding Binomials:
The Binomial Theorem
n
n
n
n
n
b
n
n
b
a
n
b
a
n
a
n
b
a 







+
+








+








+








=
+ 

...
3
1
0
)
( 2
2
1
• For any positive integer n,

7. Example
3
)
4
( +
x
• Expand
Solution:
3
2
2
3
3
4
3
3
4
*
2
3
4
*
1
3
0
3
)
4
(








+








+








+








=
+
x
x
x
x

8. Example cont.
3
)
4
( +
x
• Expand
Solution:
64
48
12
64
!
0
!
3
!
3
16
!
1
!
2
!
3
4
!
2
!
1
!
3
!
3
!
0
!
3
4
3
3
4
*
2
3
4
*
1
3
0
3
)
4
(
2
3
2
3
3
2
2
3
3
+
+
+
=
+
+
+
=








+








+








+








=
+
x
x
x
x
x
x
x
x
x
x

9. Finding a Particular Term in a Binomial
Expansion
The rth term of the expansion of (a+b)n is
1
1
1

+










r
r
n
b
a
r
n

10. Example
Find the third term in the expansion of (4x-2y)8
(4x-2y)8 n=8, r=3, a=4x, b=-2y
Solution:
2
6
2
6
2
6
1
3
1
3
8
1
1
752
,
458
4
)
4096
(
28
)
2
(
)
4
(
!
6
!
2
!
8
)
2
(
)
4
(
1
3
8
1
y
x
y
x
y
x
y
x
b
a
r
n r
r
n
=
=

=










=










+


+


11. Find the fourth term in the expansion of (3x + 2y)7
.
Text Example
7
3






(3x)7 3
(2y)3
=
7
3






(3x)4
(2y)3
=
7!
3!(7  3)!
(3x)4
(2y)3
Solution We will use the formula for the rth term of the expansion (a + b)n
,
to find the fourth term of (3x + 2y)7
. For the fourth term of (3x + 2y)7
,
n = 7, r = 4, a = 3x, and b = 2y. Thus, the fourth term is
7!
3!4!
(81x4
)(8y3
) =
7 6  5 4!
3 2 1 4!
(81x 4
)(8y3
) = 35(81x 4
)(8y3
) = 22,680x 4
y3