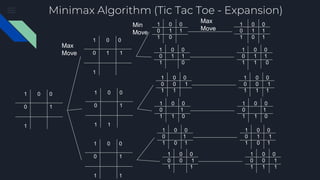
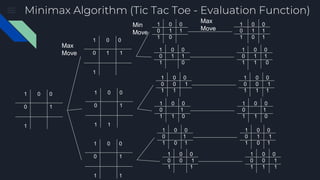
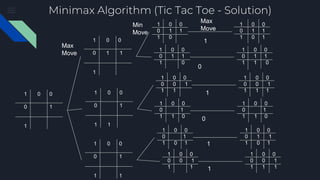
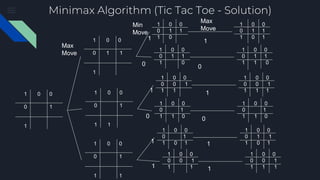
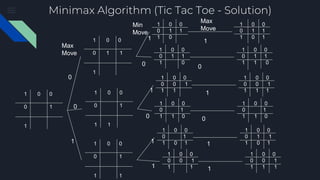
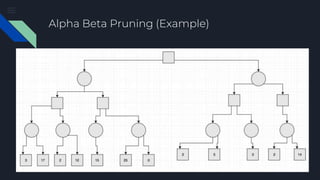
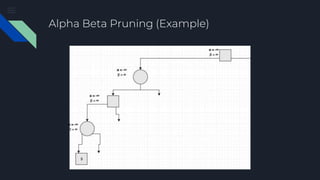
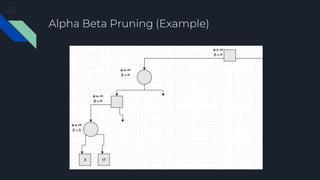
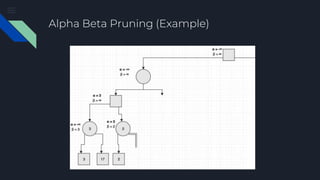
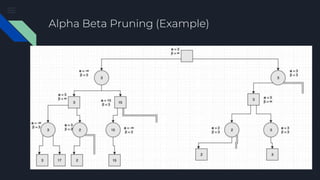
The document describes the Minimax algorithm applied to Tic Tac Toe, detailing the evaluation function at leaf nodes and the transfer of values between min and max nodes. It also covers the implementation of alpha-beta pruning to optimize the algorithm by reducing the number of nodes evaluated in the minimax tree. Examples of the algorithm's application and the pruning process are provided to illustrate its effectiveness.

1. Game Playing
Algorithm
By - Er. Suraj Awal

2. Minimax Algorithm (Tic Tac Toe)
Initial State:
1 0 0
0 1
1
Evaluation Function at Leaf
Node : 1 for win and 0 for draw
Transfer of evaluation function:
- Min node → min value
- Max node → max value

3. Minimax Algorithm (Tic Tac Toe - Expansion)
1 0 0
0 1
1
1 0 0
0 1 1
1
1 0 0
0 1
1 1
1 0 0
0 1
1 1
Max
Move
1 0 0
0 1 1
1 0
1 0 0
0 1 1
1 0
1 0 0
0 0 1
1 1
1 0 0
0 1
1 1 0
1 0 0
0 1
1 0 1
1 0 0
0 0 1
1 1
1 0 0
0 1 1
1 0 1
1 0 0
0 1 1
1 1 0
1 0 0
0 0 1
1 1 1
1 0 0
0 1
1 1 0
1 0 0
0 1 1
1 0 1
1 0 0
0 0 1
1 1 1
Max
Move
Min
Move

4. Minimax Algorithm (Tic Tac Toe - Evaluation Function)
1 0 0
0 1
1
1 0 0
0 1 1
1
1 0 0
0 1
1 1
1 0 0
0 1
1 1
Max
Move
1 0 0
0 1 1
1 0
1 0 0
0 1 1
1 0
1 0 0
0 0 1
1 1
1 0 0
0 1
1 1 0
1 0 0
0 1
1 0 1
1 0 0
0 0 1
1 1
1 0 0
0 1 1
1 0 1
1 0 0
0 1 1
1 1 0
1 0 0
0 0 1
1 1 1
1 0 0
0 1
1 1 0
1 0 0
0 1 1
1 0 1
1 0 0
0 0 1
1 1 1
Max
Move
Min
Move

5. Minimax Algorithm (Tic Tac Toe - Solution)
1 0 0
0 1
1
1 0 0
0 1 1
1
1 0 0
0 1
1 1
1 0 0
0 1
1 1
Max
Move
1 0 0
0 1 1
1 0
1 0 0
0 1 1
1 0
1 0 0
0 0 1
1 1
1 0 0
0 1
1 1 0
1 0 0
0 1
1 0 1
1 0 0
0 0 1
1 1
1 0 0
0 1 1
1 0 1
1 0 0
0 1 1
1 1 0
1 0 0
0 0 1
1 1 1
1 0 0
0 1
1 1 0
1 0 0
0 1 1
1 0 1
1 0 0
0 0 1
1 1 1
Max
Move
Min
Move
1
1
1
1
0
0

6. Minimax Algorithm (Tic Tac Toe - Solution)
1 0 0
0 1
1
1 0 0
0 1 1
1
1 0 0
0 1
1 1
1 0 0
0 1
1 1
Max
Move
1 0 0
0 1 1
1 0
1 0 0
0 1 1
1 0
1 0 0
0 0 1
1 1
1 0 0
0 1
1 1 0
1 0 0
0 1
1 0 1
1 0 0
0 0 1
1 1
1 0 0
0 1 1
1 0 1
1 0 0
0 1 1
1 1 0
1 0 0
0 0 1
1 1 1
1 0 0
0 1
1 1 0
1 0 0
0 1 1
1 0 1
1 0 0
0 0 1
1 1 1
Max
Move
Min
Move
1
1
1
1
0
0
1
1
1
1
0
0

7. Minimax Algorithm (Tic Tac Toe - Solution)
1 0 0
0 1
1
1 0 0
0 1 1
1
1 0 0
0 1
1 1
1 0 0
0 1
1 1
Max
Move
1 0 0
0 1 1
1 0
1 0 0
0 1 1
1 0
1 0 0
0 0 1
1 1
1 0 0
0 1
1 1 0
1 0 0
0 1
1 0 1
1 0 0
0 0 1
1 1
1 0 0
0 1 1
1 0 1
1 0 0
0 1 1
1 1 0
1 0 0
0 0 1
1 1 1
1 0 0
0 1
1 1 0
1 0 0
0 1 1
1 0 1
1 0 0
0 0 1
1 1 1
Max
Move
Min
Move
1
1
1
1
0
0
1
1
1
1
0
0
0
0
1

8. Alpha Beta Pruning (Example)
Range:
Alpha < N < Beta

9. Alpha Beta Pruning (Example)

10. Alpha Beta Pruning (Example)
Initially, assign alpha and beta to negative infinity and infinity
respectively.
Pass the valid bound to the first leaf node using depth first search
technique.

11. Alpha Beta Pruning (Example)

12. Alpha Beta Pruning (Example)
When we reach to the first leaf node, we run the evaluation function and
get the value of 3.
We pass back to the min node above. Since it is min node, we decrease
beta value to 3.
Next, we generate the next child from that node and run evalutation
function and return a value of 17 to the min node. Since, beta can never
increase at min node, the value of beta remains 3.

13. Alpha Beta Pruning (Example)

14. Alpha Beta Pruning (Example)
The value 3 from the min node is passed to max node above. So, alpha
becomes 3.
Get the next child and pass the bounds along. Same process as before
is repeated and we get alpha = 3 and beta = 2 at first child min node.
Since the bound can never be found i.e a number greater than alpha (3)
and less than beta (2), we stop evaluating further and other childs from
that node are pruned. This is called beta pruning. It returns the beta
value (2) to the parent max node. As max node can not decrease value
of alpha, it remains as it is i.e. 3.

15. Alpha Beta Pruning (Example)

16. Alpha Beta Pruning (Example)
Following the same process, at the end of the algorithm, we obtain:

17. Alpha Beta Pruning (Example)

18. The End!
Like, Comment and
Share