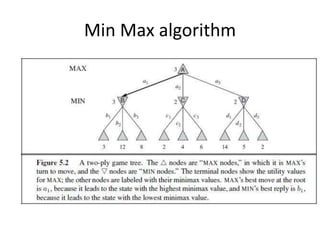
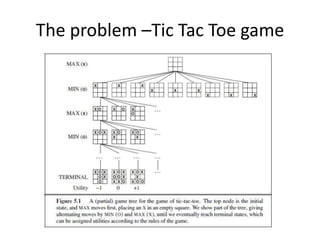
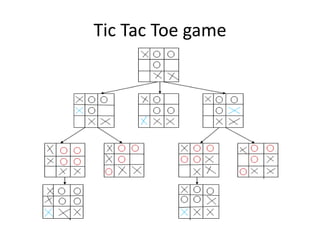
The document describes the minimax algorithm and alpha-beta pruning for a Tic Tac Toe game. It explains that minimax finds the best possible move by assuming the opponent plays optimally to minimize utility. Alpha-beta pruning improves upon minimax by pruning branches that cannot influence the final decision. It then provides pseudocode for the minimax and alpha-beta algorithms. Finally, it shows code for implementing a Tic Tac Toe game that uses minimax with alpha-beta pruning to choose moves.

1. ACI – Lab Session 2
Min Max algorithm with
Alpha-Beta pruning
For
Tic Tac Toe

2. Min Max algorithm
• An algorithm for calculating minimax decisions.
• It returns the action corresponding to the best possible
move, that is, the move that leads to the outcome with
the best utility, under the assumption that the
opponent plays to minimize utility.
• The functions MAX-VALUE and MIN-VALUE go through
the whole game tree, all the way to the leaves, to
determine the backed-up value of a state.
• The notation argmaxa∈ S f(a) computes the element a of
set S that has the maximum value of f(a).

3. Min Max algorithm

4. Alpha Beta pruning
• The problem with minimax search is that the
number of game states it has to examine is
exponential in the depth of the tree.
• We can effectively cut it in half without looking at
every node in the game tree.
• The particular technique we examine is called
ALPHA–BETA pruning.
• When applied to a standard PRUNING minimax
tree, it returns the same move as minimax would,
but prunes away branches that cannot possibly
influence the final decision.

5. Alpha Beta pruning
• α = the value of the best (i.e., highest-value) choice we
have found so far at any choice point along the path for
MAX.
• β = the value of the best (i.e., lowest-value) choice we
have found so far at any choice point along the path for
MIN.
• Alpha–beta search updates the values of α and β as it
goes along and prunes the remaining branches at a
node (i.e., terminates the recursive call) as soon as the
value of the current node is known to be worse than
the current α or β value for MAX or MIN, respectively

7. The problem –Tic Tac Toe game

8. Tic Tac Toe game

9. TIC TAC TOE WITH MIN MAX
ALGORITHM AND ALPHA BETA
PRUNING IN PYTHON
Code Walk through

10. #Class TicTacToe
• from math import inf as infinity
• class TicTacToe:
• def __init__(self):
• self.initialize_board()
• def initialize_board(self):
• self.current_state = [['-','-','-'],
• ['-','-','-'],
• ['-','-','-']]
• # Player X always plays first
• self.player_turn = 'X'

11. #Class TicTacToe – Draw the board
• def draw_board(self):
• for i in range(0, 3):
• for j in range(0, 3):
• print('{}|'.format(self.current_state[i][j]),
end=" ")
• print()
• print()

12. # Determines if the made move is a
legal move
• def is_validmove(self, px, py):
• if px < 0 or px > 2 or py < 0 or py > 2:
• return False
• elif self.current_state[px][py] != '-':
• return False
• else:
• return True

13. # Checks if the game has ended and returns the
winner in each case - #is_endofgame() function
• def is_endofgame(self):
• # Check for column-wise win
• for i in range(0, 3):
• if (self.current_state[0][i] != '-' and
• self.current_state[0][i] ==
self.current_state[1][i] and
• self.current_state[1][i] ==
self.current_state[2][i]):
• return self.current_state[0][i]

14. is_endofgame() function
• # Check for row-wise win
• for i in range(0, 3):
• if (self.current_state[i] == ['X', 'X', 'X']):
• return 'X'
• elif (self.current_state[i] == ['O', 'O',
'O']):
• return 'O'

15. # is_endofgame() function
• # Check for win over the Main diagonal
• if (self.current_state[0][0] != '-' and
• self.current_state[0][0] ==
self.current_state[1][1] and
• self.current_state[0][0] ==
self.current_state[2][2]):
• return self.current_state[0][0]

16. # is_endofgame() function
• # Check for win over the Second diagonal
• if (self.current_state[0][2] != '-' and
• self.current_state[0][2] ==
self.current_state[1][1] and
• self.current_state[0][2] ==
self.current_state[2][0]):
• return self.current_state[0][2]

17. # is_endofgame() function
• # Is whole board full?
• for i in range(0, 3):
• for j in range(0, 3):
• # There's an empty field, we continue the game
• if (self.current_state[i][j] == '-'):
• return None
• # It's a tie!
• return '-'

18. #Max player
• def max_alpha_beta(self, alpha, beta):
• maxv = -infinity
• px = None
• py = None
• #Check for end of game
• result = self.is_endofgame()
• if result == 'X':
• return (-1, 0, 0)
• elif result == 'O':
• return (1, 0, 0)
• elif result == '-':
• return (0, 0, 0)

19. #Max player - #Testing for best remaining moves,
calculating the utility function and updating alpha
• for i in range(0, 3):
• for j in range(0, 3):
• if self.current_state[i][j] == '-':
• self.current_state[i][j] = 'O'
• (m, min_i, min_j) = self.min_alpha_beta(alpha,
beta)
• if m > maxv: #Update Maxvalue
• maxv = m
• px = i
• py = j
• #After checking reset to empty state
• self.current_state[i][j] = '-'

20. #Max player -#Testing for best remaining moves,
calculating the utility function and updating alpha
• # Next two ifs in Max and Min are the only
difference between regular algorithm and alpha-
beta
• if maxv >= beta:
• return (maxv, px, py)
• #Update alpha
• if maxv > alpha:
• alpha = maxv
• return (maxv, px, py)

21. #Min player
• def min_alpha_beta(self, alpha, beta):
• minv = infinity
• qx = None
• qy = None
• #Check for end of game
• result = self.is_endofgame()
• if result == 'X':
• return (-1, 0, 0)
• elif result == 'O':
• return (1, 0, 0)
• elif result == '-':
• return (0, 0, 0)

22. CALLING ALL GAME

23. #Play tic tac toe
• def play_alpha_beta(self):
• while True:
• self.draw_board()
• self.result = self.is_endofgame()
• if self.result != None:
• if self.result == 'X':
• print('The winner is X!')
• elif self.result == 'O':
• print('The winner is O!')
• elif self.result == '-':
• print("It's a tie!")
• self.initialize_board()
• return

24. #Playing the game (Min turn)
• #px, py, qx and qy represent the board positions as x and y
coordinates
• if self.player_turn == 'X':
• while True:
• (m, qx, qy) = self.min_alpha_beta(-infinity, infinity)
• px = int(input('Insert the X coordinate: '))
• py = int(input('Insert the Y coordinate: '))
• qx = px
• qy = py
• if self.is_validmove(px, py):
• self.current_state[px][py] = 'X'
• self.player_turn = 'O'
• break
• else:
• print('The move is not valid! Try again.')

25. #Playing the game (Max turn)
• else:
• (m, px, py) =
• self.max_alpha_beta(-infinity, infinity)
• self.current_state[px][py] = 'O'
• self.player_turn = 'X'
•

26. Thank you
That’s all for the day