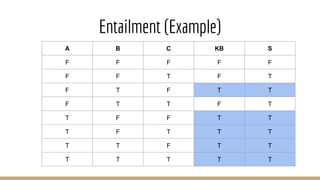
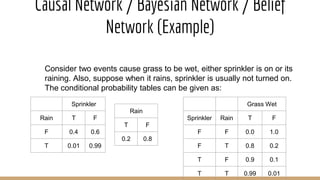
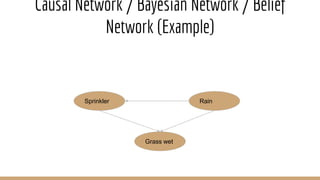
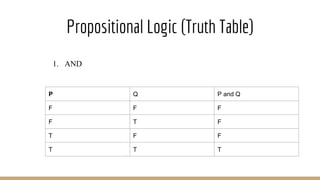
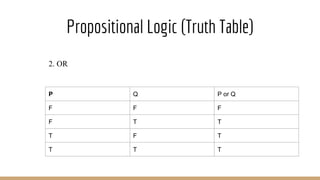
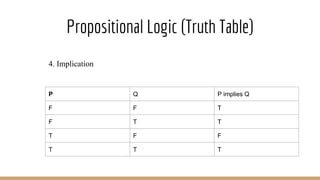
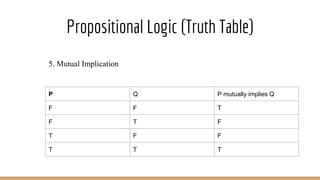
The document discusses knowledge representation, including the types of knowledge such as procedural, declarative, and heuristic, and the use of formal logic for inference and reasoning. It explains propositional and predicate logic, the skolemization process, conjunctive normal form, and resolution refutation processes for knowledge inference. Additionally, it covers rule-based systems, entailment, and Bayesian networks for probabilistic reasoning.

1. Knowledge
Representation,
Inference and
Reasoning
By - Er. Suraj Awal

2. Knowledge
- Knowledge is the individual’s understanding of a given subject that can be used to
solve the problems of a particular domain
- It is the part of the information that is extracted, analyzed and represented in a very
special way
- Knowledge representation is the process of expressing knowledge about the world in
a computer tractable form.
- A formal language which consists of formal symbols are used for knowledge
representation

3. Knowledge
- Fact is the truth about the real world
- The collection of facts from a domain provides the knowledge of that domain
- These facts should be represented and it can be done at two levels:
a) Knowledge level (Facts are described)
b) Symbol level (Mathematical representation of knowledge)

4. Types of Knowledge
1. Procedural Knowledge - Information that is processed
2. Declarative Knowledge - Information in the form of fact statements
3. Heuristic Knowledge - Informations used to make judgements

5. Logic
- Formal language that is used to express knowledge and ways of reasoning about the
world that is either true or false but not both at the same time.
- It is defined by:
1. Syntax (possible configuration that constitute sentences)
2. Semantic (interpretation of sentence about the world)
3. Proof theory (set of rules to inference new knowledge from the old one)

6. Propositional Logic
- Propositional logic is the logic that express knowledge at the
sentential level.
- Proposition is the declarative statement which can either be true or
false but not both at the same time.
- Provides mathematical model to reason about the logical expression
as true or false
- Atomic propositions are the statements constructed from constants
and propositional symbols
- Composite propositions are the statements constructed using valid
atomic propositions connected via connectives

7. Propositional Logic (Connectives)
1. AND
2. OR
3. NOT
4. Implies or If….Then
5. Mutual Implication

8. Propositional Logic (Truth Table)
1. AND
P Q P and Q
F F F
F T F
T F F
T T T

9. Propositional Logic (Truth Table)
2. OR
P Q P or Q
F F F
F T T
T F T
T T T

10. Propositional Logic (Truth Table)
3. NOT
P Not P
F T
T F

11. Propositional Logic (Truth Table)
4. Implication
P Q P implies Q
F F T
F T T
T F F
T T T

12. Propositional Logic (Truth Table)
5. Mutual Implication
P Q P mutually implies Q
F F T
F T F
T F F
T T T

13. Propositional Logic (Well Defined Formula)
- A proposition is known as a well defined formula if:
1. A symbol is a sentence
2. If s is a sentence, then not s is a sentence
3. If s is a sentence, then (s) is a sentence
4. If s and T are sentences, then (s not T), (s or T), (s and T) and (s ⇔
T) are sentences

14. Tautology, Contradiction and Satisfiable
- Tautology is the notation in formal language which is always true
- Contradiction is the notation in formal language which is always
false
- If at least one sentence in the set is true, then it is satisfiable

15. Logical Equivalence
- If two propositions P and Q have same truth values in every possible
case, the propositions are called logically equivalent.
- If p, q and r are statements, then:
1. ˥ ( ˥ p ) Ξ p : Double Negation Rule
2. ˥(p˅q) Ξ (˥p)^(˥q) : De-Morgan’s Law
3. ˥(p^q) Ξ (˥p)˅(˥q) : De-Morgan’s Law
4. P^(q˅r) Ξ (p^q)˅(p^r) : distribution law
5. P˅(q^r) Ξ (p˅q)^(p˅r) : distribution law

16. Predicate Logic
- Predicate logic allows flexible knowledge representation
- In terms of objects, properties, relations and functions
- The symbols denote properties of an object or relation between
objects
- First Order Predicate Logic (FOPL) makes use of quantified variables
over objects.

17. Quantifiers
1. Universal Instantiation
∀ x : p(x) implies p(c) for all c
1. Universal Generalization
p(c) for all c implies ∀ x : p(x)
1. Existential Instantiation
∃ x : p(x) implies p(c) for some c
1. Existential Generalization
p(c) for some c implies ∃ x : p(x)

18. Skolemization Process
- It is a substitution process that eliminates existential quantifiers by
replacing them with some SKOLEM functions
- All the quantifiers should first be moved to the left side in proper
order

19. Skolemization Process (Algorithm)
1. If the leftmost quantifier in an expression is an existential quantifier,
we replace all occurrences of the variable it quantifies with an
arbitrary constant not appearing elsewhere in the expression and
delete the quantifier.
2. For each existential quantifier which is preceded by one or more
universal quantifiers, we replace all occurrences of the existentially
quantified variable by a function not appearing elsewhere in the
expression. The arguments of such function should match all the
variables appearing in each universal quantifier which preceed the
existential quantifier.

20. Skolemization Process (Example)
∃ x ∃ y ∀ u ∀ v ∃ z ∀ w ∃ s : P (x, y, v, z, w) ^ Q (s, u, x, z)
Solution,
∀ u ∀ v ∀ w : P (a, b, v, f(u, v), w) ^ Q (g(u, v, w), u, a, f(u, v))

21. Conjunctive Normal Form (CNF)
1. Eliminate => by using : (a => b) Ξ ˥a ˅ b
2. Reduce scope of ˥ to a single term using:
- ˥(˥a) Ξ a
- ˥(a^b) Ξ ˥a ˅ ˥b
- ˥(a v b) Ξ ˥a ^ ˥b
- ˥ ∀ x : p(x) Ξ ∃ x : ˥p(x)
- ˥ ∃ x : p(x) Ξ ∀ x : ˥p(x)
1. Standardize variables so that each quantifiers binds a unique variable
- ∀ x : (p(x) v q(x)) Ξ ( ∀ x : p(x) v ∀ x : q(x) )

22. Conjunctive Normal Form (CNF)
4. Move all quantifiers to left without changing the relative order
5. Eliminate existential quantifiers by substituting a variable that produces
a desired value using skolemization process
6. Drop the prefix
7. Convert matrix into conjunction of disjoints:
(a^b)˅c Ξ (a˅c) ^ (b^c)
8. Create separate clause corresponding to each conjunct
9. Standardize apart the variables in the set of clauses

23. Horn Clause
- Horn clause is a clause with at most one positive literal
- A horn clause with exactly one positive literal is called definite
clause
- A horn clause with no positive literal is called goal clause
- A horn formula is a CNF whose all clauses are are horn clauses.
- Example : ˥a v ˥b v ˥c v ˥d v ˥e v ˥f v g
- It can be represented as : ( a ^ b ^ c ^ d ^ e ^ f ) ⇒ g
- Such representation are common in logic programming

24. Resolution Refutation Process
- Resolution is the process of that produces proof by refutation which
involves operating on the statements that have been converted to the
clause form.
- It proves a statement by attempting to show that the negation of a
statement produces a contradiction with the known statement.

25. Resolution Refutation Process (Algorithm)
1. Represent the facts using First Order Predicate Logic (FOPL)
2. Convert the predicates into clause form (Conjunctive Normal Form)
3. Repeat:
a) Select two clauses
b) Resolve them together
c) If resolvent is empty, contradiction occurs. Else, add it to set of
clauses.

26. Resolution Refutation Process (Example)
If X is on top of Y, Y supports X. If X is above Y and they are touching
each other, X is on top of Y. A cup is above a book. A cup is touching a
book. Show that supports(book, cup) is true.
Using Resolution Refutation process, prove the above knowledge
inference.

27. Resolution Refutation Process (Example)
Representation in FOPL:
1. ∀ x : ∀ y : top_of(X, Y) → supports(Y, X)
2. ∀ x : ∀ y : above(X, Y) ^ touch(X, Y) → top_of(X, Y)
3. above(cup, book)
4. touch(cup,book)
To prove : supports(book, cup)

28. Resolution Refutation Process (Example)
Conversion to Clause Form (CNF) :
1. ˥ top_of(X1 , Y1) v supports(Y1 , X1)
2. ˥ above(X2 , Y2) v ˥ touch(X2 , Y2) v top_of(X2 , Y2)
3. above(cup, book)
4. touch(cup, book)
To prove : supports(book, cup)

29. Resolution Refutation Process (Example)
Resolution Refutation :
Assume, ˥ supports(book, cup) is True.
Now,
Using assumption and clause form (1), putting book/Y1 and cup/X1 , we
get:
˥ top_of(cup, book) --------- (5)

30. Resolution Refutation Process (Example)
Using clause form (2) and knowledge (5), putting book/Y2 and cup/X2 ,
we get:
˥ above(cup, book) v ˥ touch(cup, book) -------- (6)
Using knowledges (6) and (3), we get:
˥ touch(cup, book) --------- (7)

31. Resolution Refutation Process (Example)
Using knowledges (7) and (4), we get:
< Null >
Since contradiction occurs, our assumption is false.
Hence, supports(book, cup) is true.

32. Rule Based System
- Automatic problem solving tool that combines human expertise and
decision making
- Expressed as antecedent-consequent rules
- Solve problems by selecting relevant rules and combining the results
- Determine the best sequence of rules
- Modus Ponen : [ p ^ ( p → q ) ] → q

33. Forward Chaining
- Inference using repeated application of modus ponens
- Starts with available data
- Uses inference rules until a goal is reached
- Searches the rules until it finds one in which antecedent is true, then
concludes the consequent and adds new information to its data.

34. Backward Chaining
- Inference using repeated application of modus ponens
- Starts from the goals
- Uses inference rules until data is obtained
- Implements depth first search strategy
- Searches the rules until it finds one in which consequent is true, then
concludes the antecedent and adds new information to its data.

35. Rule Based System (Example)
Consider the rule base as:
1. If X croaks and eats flies, X is a frog.
2. If X chirps and sings, X is a Canary.
3. If X is a frog, then X is green.
4. If X is a Canary, then X is yellow.
Conclude color of Fritz, given he croaks and eats flies.

36. Rule Based System (Example)
Forward Chaining:
Fritz croaks and eats flies (Data)
Fritz is a frog
Fritz is green (Goal)

37. Rule Based System (Example)
Backward Chaining:
Color of Fritz (Goal)
Fritz is green
Fritz is yellow
Fritz is frog
Fritz is Canary

38. Entailment
- Relationship between current knowledge and new knowledge
inferred from current knowledge.
- Reflects that one fact follows from the others.
- Knowledge Base (KB) entails a sentence if and only if : the sentence
is true in all the world where KB is true.

39. Entailment (Example)
Consider Knowledge Base (KB) as:
A v B
˥ C v A
Consider a new sentence, S : A v B v C
Show that KB |- S ( KB entails S)

40. Entailment (Example)
A B C KB S
F F F F F
F F T F T
F T F T T
F T T F T
T F F T T
T F T T T
T T F T T
T T T T T

41. Entailment (Example)
From the truth table, whenever KB is true, S is also true. So, we can
say that KB entails S i.e. KB |- S.

42. Probability and Bayes Theorem
- Statistical theory of evidence, based on conditional probability
- Bayes theorem states that:
P(Hi | E) = P(E | Hi) * P(Hi)
Σ(n=1 to k) P(E | Hn) * P(Hn)
Where,
P(Hi | E) = Prob. that Hi is true given evidence E
P(E | Hi) = Prob. that evidence E is observed given Hi is true
P(Hi) = Prob. that Hi is true in absence of evidence
K = number of hypotheses

43. Causal Network / Bayesian Network / Belief
Network
- Probabilistic graphical model that represents a set of random
variables and their conditional dependencies.
- Uses directed acyclic graph.
- Nodes represent the random variables
- Edges represent conditional dependencies

44. Causal Network / Bayesian Network / Belief
Network (Example)
Consider two events cause grass to be wet, either sprinkler is on or its
raining. Also, suppose when it rains, sprinkler is usually not turned on.
The conditional probability tables can be given as:
Sprinkler
Rain T F
F 0.4 0.6
T 0.01 0.99
Rain
T F
0.2 0.8
Grass Wet
Sprinkler Rain T F
F F 0.0 1.0
F T 0.8 0.2
T F 0.9 0.1
T T 0.99 0.01

45. Causal Network / Bayesian Network / Belief
Network (Example)
The situation can be modelled using Bayesian or Causal or Belief
network as shown in below graph:
Sprinkler Rain
Grass wet

46. Causal Network / Bayesian Network / Belief
Network (Example)
Q. Calculate the probability that it is raining, given the grass is wet?
P(R=T | G=T) = Σ(S = {T, F})P(G=T, S, R=T) = 35.77%
(0.3577)
Σ(S,R = {T, F})P(G=T, S, R)
Use the formula : P(G, S, R) = P(G|S, R) * P(S|R) * P(R)

47. The End !!!