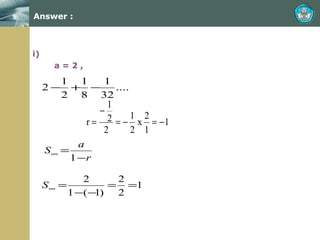
The document discusses sequences and series, including sigma notation, arithmetic sequences and series, and geometric sequences and series. It defines sequences, finite and infinite sequences, and series. It provides the formulas for the nth term and nth partial sum of arithmetic and geometric sequences. It also gives examples of applying arithmetic and geometric series to problems involving patterns, sums, and compound interest.

1. SIGMA NOTATIOM, SEQUANCES AND SERIES

2. MAIN TOPIC 4.1 Sequences and Series 4.2 Sigma Notation 4.3 Arithmetic Sequences and Series 4.3 Geometric Sequences and Series 4.4 Infinite Geometric Series

3. OBJECTIVE At the end of this topic you should be able to Define sequences and series Understand finite and infinite sequence, finite and infinite series Use the sum notation to write a series

4. SEQUENCES and SERIES A sequence is a set of real numbers a 1, a 2,… an ,… which is arranged (ordered). Example: Each number ak is a term of the sequence. We called a 1 - First term and a 45 - Forty-fifth term The n th term an is called the general term of the sequence.

5. INFINITE SEQUENCES An infinite sequence is often defined by stating a formula for the n th term, a n by using { a n } . Example: The sequence has n th term . Using the sequence notation, we write this sequence as follows First three terms Fifth teen term INFINITE SEQUENCES

6. EXERCISE 1 : Finding terms of a sequence List the first four terms and tenth term of each sequence: A B C D E F

7. Definition of Sigma Notation Consider the following addition : Based on the patterns of the addends, the addition above can be written in the following form 2 + 5 + 8 + 11 + 14 = (3(1) – 1) + (3(2) – 1) + (3(3) – 1) + (3(4) – 1) + (3(5) – 1) + (3(6) – 1) 2 + 5 + 8 + 11 + 14

8. The amount of the term in the addition above can be written as (3i – 1). The term in the addition are obtained by substituting the value of i with the value of 1, 2, 3, 4, and 5 to (3i – 1) The symbol read as sigma, is used to simplify the expression of the addition of number with certain patterns. In order that you understand more, the addition above can be written as : = 2 + 5 + 8 + 11 + 14 =(3(1) – 1) + (3(2) – 1) + (3(3) – 1) + (3(4) – 1) + (3(5) – 1) + (3(6)-1) =(3(1) – 1) + (3(2) – 1) + … + (3(i) – 1) + … + (3(6)-1)

9. In general, the sum of n term of number with certain pattern where the i th term is stated as U i can be written as : U 1 + U 2 + U 3 + … + U i + …+ U n = Where : i = 1 is the lower bound of the addition n is the upper bound of the addition

10. Example 1 : Change the following of addition in the form of sigma notation! a. 3 + 6 + 9 + 12 + 15 + 18 + 21 b. 1 + 5 + 9 + 13 + 17 + 21

11. Answer : 3 + 6 + 9 + 12 + 15 + 18 + 21 = 3(1) + 3(2) + 3(3) + 3(4) + 3(5) + 3(6) + 3(7) = 3(1) + 3(2) + … + 3(i) + … + 3(7) = 1 + 5 + 9 + 13 + 17 + 21 = (4(1) – 3) + (4(2) – 3) + (4(3) – 3) + … + (4(6) – 3) = (4(i) – 3) =

12. Determine the value of the following addition that state in sigma notation! a. b.

13. Answer :

14. THEOREM OF SUMS Sum of a constant Sum of 2 infinite sequences

15. Arithmetic Sequence and Series

16. OBJECTIVE At the end of this topic you should be able to : Recognize arithmetic sequences and series Determine the n th term of an arithmetic sequences and series Recognize and prove arithmetic mean of an arithmetic sequence of three consecutive terms a , b and c

17. THE n th TERM OF AN ARITHMETIC SEQUENCES An arithmetic sequence with first term a and common different b , can be written as follows: The n th term, a n of this sequence is given by the following formula: a, a + b, a + 2b, … , a + (n – 1)b U n = a + (n – 1)b

18. ARITHMETIC SEQUENCES A sequence U 1 , U 2 ,… U n ,… is an arithmetic sequence if there is a real number b such that for every positive integer k , The number is called the common difference of the sequence. U 2 – U 1 = U 3 – U 2 = … = U n – U n-1 = a constant b = U 2 – U 1

19. Example 1: Find the formula for the and term if given the arithmetic sequence : A. 1, 4, 7, 10, … B. 53, 48, 43, …

20. Answer : A 1, 4, 7, 10 Based on the sequence, then obtained : a = 1, b = U2 – U1 = 4 – 1 = 3 Un = a + (n – 1)b = 1 + (n – 1)3 = 1 + 3n – 1 = 3n U30 = 3n = 3(30) = 90

21. Answer : B 53, 48, 43, … Based on the sequence, then obtained : a = 53, b = U2 – U1 = 48 – 53 = -5 Un = a + (n – 1)b = 48 + (n – 1)-5 = 48 + (-5n + 5) = 48 – 5n + 8 = 53 – 5n U30 = 53 – 5n = 53 – 5(30) = 53 – 150 = -97

22. EXERCISE 9: Finding a specific term of an arithmetic sequence If given the arithmetic sequence U 6 = 50 and U 41 = 155 determine the twelfth. If the fourth term of an arithmetic sequence is 5 and the ninth term is 20, find the sixth term.

23. Answer : A U6 = 50, U21 = 155, U12? U6 = a + 5b = 50 U21 = a + 20b = 155 -15b = -105 b = 7 a + 5b = 50 a + 5(7) = 50 a = 50 - 35 a = 15 U30 = a + (n – 1)b = 15 + (29)7 = 15 + 203 = 218

24. Answer : A U4 = 5, U9 = 20, U6? U4 = a + 3b = 5 U9 = a + 8b = 20 -5b = -15 b = 3 a + 3b = 5 a + 3(3) = 5 a = 5 - 9 a = -4 U6 = a + (n – 1)b = -4 + (5)3 = -4 + 15 = 11

25. Formula for the middle Term of on Arithmetic Sequence

26. Example : Given an arithmetic sequence of 3, 8, 13, … , 283. Determine the middle term of the sequence. Which term is the middle term

27. Answer : From the question it is know that U1 = 3 and Un = 283 So the middle term is U t = 143 U t = 143 a + (t – 1)b = 143 3 + (t – 1)5 = 143 (t – 1)5 = 140 t – 1 = 28 t = 29

28. THE n th PARTIAL SUM OF AN ARITHMETIC SEQUENCES If a 1, a 2,… an ,… is an arithmetic sequence with common difference b, then the n th partial sum Sn (that is the sum of the first n th terms) is given by either or

29. OBJECTIVE At the end of this topic you should be able to Recognize geometric sequences and series Determine the n th term of a geometric sequences and series Recognize and prove geometric mean of an geometric sequence of three consecutive terms a , b and c Derive and apply the summation formula for infinite geometric series Determine the simplest fractional form of a repeated decimal number written as infinite geometric series

30. GEOMETRIC SEQUENCES A sequence U 1 , U 2 ,… U n ,… is a geometric sequence if U 1 ≠ 0 . The number is called the common ratio of the sequence.

31. Example : Given Geometric sequence of 24, 12, 6, 3, …, where the formula of the nth term is Un . Determine Un and the sixth term of the sequence

32. Answer: The geometric sequence of 24, 12, 6, 3, … , the first term of the sequence a = 24 and the ratio r= ½ . The formula for the nth term is :

33. THE SUM OF AN INFINITE GEOMETRIC SERIES If | r| < 1 , then the infinite geometric series has the sum

34. THE n th PARTIAL SUM OF AN GEOMETRIC SEQUENCES

35. Example : Given that a geometric sequence : 2, 6, 18, 54, …, Un, Determine : a. The formula for nth term and b. The sum of the sixth n term!

36. Answer The formula for nth term is Sequence a geometric sequence : 2, 6, 18, 54, … Un Have a = 2 and r = 3 The Sum of the first n term is :

37. THE SUM OF AN INFINITE GEOMETRIC SERIES If | r| < 1 , then the infinite geometric series has the sum

38. EXERCISE 17: Find the sum of infinite geometric series The following sequence is infinite geometric series. Find the sum

39. Answer : i) a = 2 ,

40. APPLICATIONS OF ARITHMETIC AND GEOMETRIC SERIES

41. OBJECTIVE At the end of this topic you should be able to Solve problem involving arithmetic series Solve problem involving geometric series

42. APPLICATION 1: ARITHMETIC SEQUENCE A carpenter whishes to construct a ladder with nine rungs whose length decrease uniformly from 24 inches at the base to 18 inches at the top. Determine the lengths of the seven intermediate rungs. a 1 = 18 inches a 9 = 24 inches Figure 1

43. APPLICATION 2: ARITHMETIC SEQUENCE The first ten rows of seating in a certain section of stadium have 30 seats, 32 seats, 34 seats, and so on. The eleventh through the twentieth rows contain 50 seats. Find the total number of seats in the section. Figure 2

44. APPLICATION 1: GEOMETRIC SEQUENCE A rubber ball drop from a height of 10 meters. Suppose it rebounds one-half the distance after each fall, as illustrated by the arrow in Figure 3. Find the total distance the ball travels. 5 5 10 1.25 1.25 2.5 2.5 Figure 3

45. APPLICATION 2: GEOMETRIC SEQUENCE If deposits of RM100 is made on the first day of each month into an account that pays 6% interest per year compounded monthly, determine the amount in the account after 18 years. Figure 4