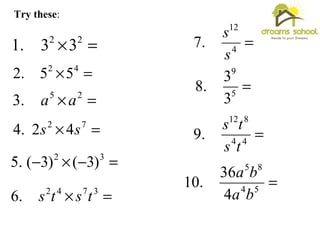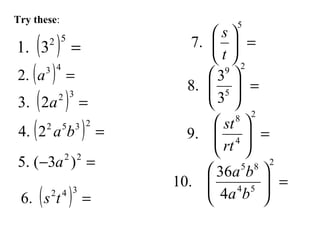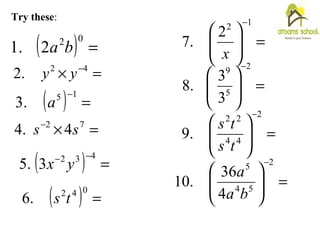This document discusses the laws of exponents. It defines what exponents mean and provides examples. The key laws of exponents covered are: 1) Multiplying powers with the same base means adding the exponents 2) Dividing powers with the same base means subtracting the exponents 3) Raising a power to another exponent means multiplying the exponents 4) A number with a zero exponent equals one. Worked examples applying each law are provided.

1. 1

3. ExponentsExponents
{ 3
5Power
base
exponent
3 3
means that is the exponential
form of t
Example:
he number
125 5 5
.125
=
53
means 3 factors of 5 or 5 x 5 x 5

4. The Laws of Exponents:The Laws of Exponents:
#1: Exponential form: The exponent of a power indicates
how many times the base multiplies itself.
n
n times
x x x x x x x x
−
= × × ×××× × × ×144424443
3
Example: 5 5 5 5= × ×
n factors of x

5. #2: Multiplying Powers: If you are multiplying Powers
with the same base, KEEP the BASE & ADD the EXPONENTS!
m n m n
x x x +
× =
So, I get it!
When you
multiply
Powers, you
add the
exponents!
512
2222 93636
=
==× +

6. #3: Dividing Powers: When dividing Powers with the
same base, KEEP the BASE & SUBTRACT the EXPONENTS!
m
m n m n
n
x
x x x
x
−
= ÷ =
So, I get it!
When you
divide
Powers, you
subtract the
exponents!
16
22
2
2 426
2
6
=
== −

7. Try these:
=× 22
33.1
=× 42
55.2
=× 25
.3 aa
=× 72
42.4 ss
=−×− 32
)3()3(.5
=× 3742
.6 tsts
=4
12
.7
s
s
=5
9
3
3
.8
=44
812
.9
ts
ts
=54
85
4
36
.10
ba
ba

8. =× 22
33.1
=× 42
55.2
=× 25
.3 aa
=× 72
42.4 ss
=−×− 32
)3()3(.5
=× 3742
.6 tsts
8133 422
==+
725
aa =+
972
842 ss =×× +
SOLUTIONS
642
55 =+
243)3()3( 532
−=−=− +
793472
tsts =++

9. =4
12
.7
s
s
=5
9
3
3
.8
=44
812
.9
ts
ts
=54
85
4
36
.10
ba
ba
SOLUTIONS
8412
ss =−
8133 459
==−
4848412
tsts =−−
35845
9436 abba =×÷ −−

10. #4: Power of a Power: If you are raising a Power to an
exponent, you multiply the exponents!
( )
nm mn
x x=
So, when I
take a Power
to a power, I
multiply the
exponents
52323
55)5( == ×

11. #5: Product Law of Exponents: If the product of the
bases is powered by the same exponent, then the result is a
multiplication of individual factors of the product, each powered
by the given exponent.
( )
n n n
xy x y= ×
So, when I take
a Power of a
Product, I apply
the exponent to
all factors of
the product.
222
)( baab =

12. #6: Quotient Law of Exponents: If the quotient of the
bases is powered by the same exponent, then the result is both
numerator and denominator , each powered by the given exponent.
n n
n
x x
y y
 
= ÷
 
So, when I take a
Power of a
Quotient, I apply
the exponent to
all parts of the
quotient.
81
16
3
2
3
2
4
44
==






13. Try these:
( ) =
52
3.1
( ) =
43
.2 a
( ) =
32
2.3 a
( ) =
2352
2.4 ba
=− 22
)3(.5 a
( ) =
342
.6 ts
=





5
.7
t
s
=





2
5
9
3
3
.8
=





2
4
8
.9
rt
st
=





2
54
85
4
36
.10
ba
ba

14. ( ) =
52
3.1
( ) =
43
.2 a
( ) =
32
2.3 a
( ) =
2352
2.4 ba
=− 22
)3(.5 a
( ) =
342
.6 ts
SOLUTIONS
10
3
12
a
6323
82 aa =×
6106104232522
1622 bababa ==×××
( ) 4222
93 aa =×− ×
1263432
tsts =××

15. =





5
.7
t
s
=





2
5
9
3
3
.8
=





2
4
8
.9
rt
st
=





2
54
85
4
36
10
ba
ba
SOLUTIONS
( ) 62232223
8199 babaab == ×
2
8224
r
ts
r
st
=





( ) 824
33 =
5
5
t
s

16. #7: Negative Law of Exponents: If the base is powered
by the negative exponent, then the base becomes reciprocal with the
positive exponent.
1m
m
x
x
−
=So, when I have a
Negative Exponent, I
switch the base to its
reciprocal with a
Positive Exponent.
Ha Ha!
If the base with the
negative exponent is in
the denominator, it
moves to the
numerator to lose its
negative sign!
93
3
1
125
1
5
1
5
2
2
3
3
==
==
−
−
and

17. #8: Zero Law of Exponents: Any base powered by zero
exponent equals one.
0
1x =
1)5(
1
15
0
0
0
=
=
=
a
and
a
and
So zero
factors of a
base equals 1.
That makes
sense! Every
power has a
coefficient
of 1.

18. Try these:
( ) =
02
2.1 ba
=× −42
.2 yy
( ) =
−15
.3 a
=×− 72
4.4 ss
( ) =
−− 432
3.5 yx
( ) =
042
.6 ts
=





−12
2
.7
x
=





−2
5
9
3
3
.8
=





−2
44
22
.9
ts
ts
=





−2
54
5
4
36
.10
ba
a

19. SOLUTIONS
( ) =
02
2.1 ba
=× −42
.2 yy
( ) =
−15
.3 a
=×− 72
4.4 ss
( ) =
−− 432
3.5 yx
( ) =
042
.6 ts
1
2
2 1
y
y =−
5
1
a
5
4s
( ) 12
8
1284
81
3
y
x
yx =−−
1

20. =





−12
2
.7
x
=





−2
5
9
3
3
.8
=





−2
44
22
.9
ts
ts
=





−2
54
5
4
36
.10
ba
a
SOLUTIONS
4
4
1
x
x
=





−
( ) 8
824
3
1
33 == −−
( ) 44222
tsts =
−−−
2
10
1022
81
9
a
b
ba =−−

21. 21
Do you find this slides were useful?
One second of your life , can bring a smile in a girl life
If Yes ,Join Dreams School “Campaign for Female Education”
Help us in bringing a change in a girl life, because “When
someone takes away your pens you realize quite how
important education is”.
Just Click on any advertisement on the page, your one
click can make her smile.
Eliminate Inequality “Not Women”
One second of your life , can bring a smile in her life!!
Do you find these slides were useful?
If Yes ,Join Dreams School “Campaign
for Female Education”
Help us in bringing a change in a girl life,
because “When someone takes away your
pens you realize quite how important
education is”.
Just Click on any advertisement on the page,
your one click can make her smile.
We our doing our part & u ?
Eliminate Inequality “Not Women”