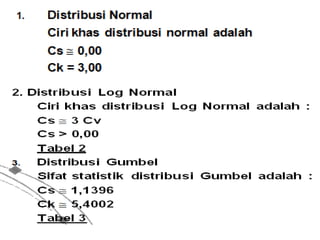
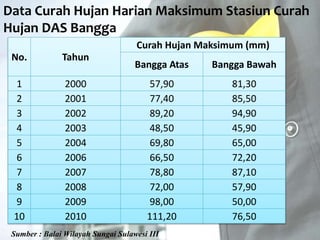
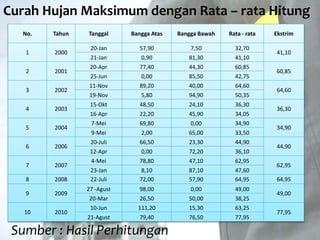
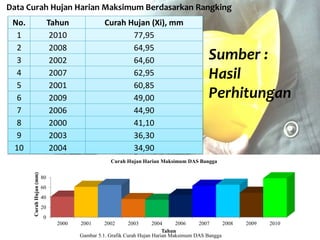
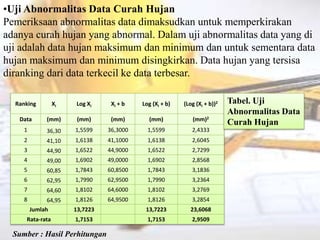
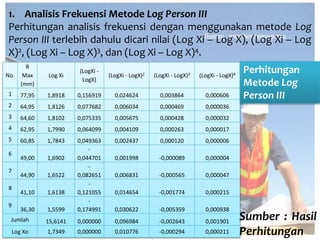
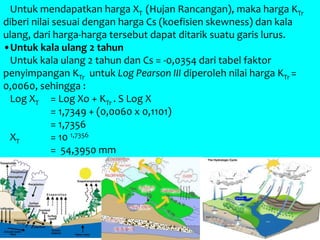
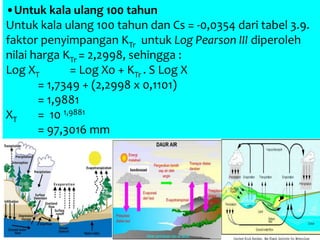
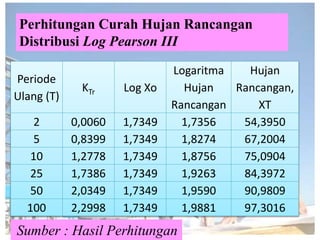
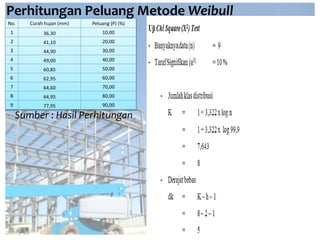
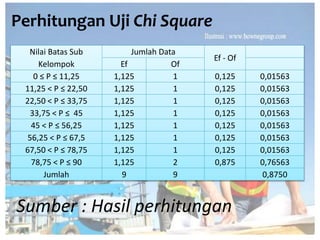
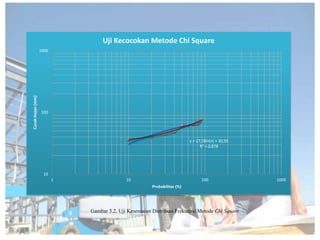
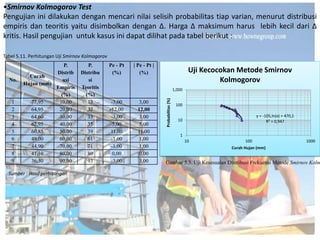
Dokumen tersebut memberikan penjelasan mengenai analisis frekuensi data hidrologi. Tujuan analisis ini adalah menganalisis besaran atau peristiwa ekstrim seperti hujan, banjir, dan kekeringan berdasarkan frekuensi kejadiannya dengan menerapkan distribusi kemungkinan. Dokumen ini juga menjelaskan langkah-langkah perhitungan analisis frekuensi seperti pemilihan agihan frekuensi, pengujian parameter statistik, dan

1. ANALISIS FREKUENSI
Disusun Oleh :
DIAN WAHYUNI WEROKILA, ST
F 112 14 006
Dosen Mata Kuliah :
Dr. Ir. I Wayan Sutapa, M. Eng

2. Hujan rencana merupakan
kemungkinan tinggi hujan yang terjadi
dalam kala ulang tertentu sebagai
hasil dari suatu rangkaian analisis
hidrologi yang biasa disebut
analisis frekuensi .
Pengertian
Analisis Frekuensi

3. TUJUAN ANALISIS FREKUENSI DATA
HIDROLOGI
Tujuan analisis frekuensi data hidrologi
adalah berkaitan dengan besaran atau
peristiwa-peristiwa ekstrim (hujan,
banjir, kekeringan, dsb) yang berkaitan
dengan frekuensi kejadiannya melalui
penerapan distribusi kemungkinan.

4. KEGUNAAN ANALISA
FREKUENSI
Untuk memperhitungkan kapasistas bangunan, saluran
drainase, irigasi, bendungan
Menentukan memperkirankan besarnya kerusakan
yang ditimbulkan oleh debit banjir, sehingga dapat
langkah-langkah pencegahan yang ditentukan
Perhitungan Ekonomi Proyek
Dengan analisis frekuensi dapat diduga
kejadian yang sama akan terulang atau
lebih besar dalam periode N tahun yang
akan datang.
1
2
3
4

5. Tabel nilai kala ulang banjir rancangan yang digunakan
Departeman Pekerjaan Umum untuk berbagai bangunan di
sungai (Srimoemi Doelchomid, 1987).
Kala ulang banjir rancangan untuk bangunan di sungai

6. Pengujian Parameter Statistik Analisis Frekuensi
(Soewarno, 1995) :
KOEFISIEN VARIASI (CV)
KOEFISIEN SKEWNESS/PENYIMPANGAN (CS)
KOEFISIEN KURTOSIS (CK)

7. Pengujian Kesesuaian Distribusi Frekuensi
Uji Chi - Square (X2) Test
Uji Smirnov Kolmogorov
Langkah Perhitungan Analisis Frekuensi:
Pemilihan Agihan Frekuensi
Pemilihan Jenis Sebaran
Metode Log Normal
1
2
Metode Gumbell
Metode Log Person III
Syarat untuk EJ. Gumbell,
Ck = 5,40 dan Cs = 1,14,
Log Pearson III harga Cs
dan Cvnya bebas, dan untuk
Log Normal Cs = 0,00.

9. 1
Pemilihan Agihan Frekuensi1
Adapun langkah-langkah dalam pemilihan agihan
frekuensi adalah (Subarkah, 1980):
•Menghitung curah hujan maksimum rerata dengan
persamaan :


n
i
io X
n
X
1
1
•Menghitung simpangan baku, dengan persamaan :
 
1
1
2




n
XX
S
n
i
oi
x

10. •Menghitung parameter statistik yang meliputi koefisien
skewness/penyimpangan (Cs), koefisien varians (Cv)
dan koefisien kurtosis (Ck) dengan persamaan :
 
   3
1
3
21 x
n
i
oi
s
Snn
XXn
C




 
    3
1
42
321 x
n
i
oi
k
Snnn
XXn
C




o
x
v
X
S
C 

11. Keterangan :
Xi = curah hujan (mm)
Xo = curah hujan rata-rata (mm)
n = jumlah data
Sx = standar deviasi
Cs = koefisien skewnes/ penyimpangan
Cv = koefisisen varians
Ck = koefisien kurtoris
Berdasarkan harga Cs, Ck dan Cv
yang diperoleh maka dapat
ditentukan agihan frekuensi yang
akan digunakan

12. Pengujian Kesesuaian
Distribusi Frekuensi
2
•Uji Chi - Square (X2) Test
Uji chi square dimaksudkan untuk
menentukan apakah persamaan
distribusi peluang yang telah
dipilih dapat mewakili dari
distribusi statistik sampel data
yang dianalisis

13.  
Ef
OfEfK
i
hX
2
1
2 



14. Interpretasi hasil dari uji chi square adalah :
•Apabila peluang lebih besar dari 5%, maka persamaan
distribusi teoritis yang digunakan dapat diterima.
•Apabila peluang lebih kecil 1%, maka persamaan distribusi
teoritis yang digunakan tidak dapat diterima.
•Apabila peluang berada diantara 1 - 5% adalah tidak
mungkin mengambil keputusan, misal perlu penambahan
data.

15. •Uji Smirnov Kolmogorov
(Pmax | Pe –Pt | ) < ΔCr, α
Pada umumnya taraf signifiksi atau derajat
nyata (α) diambil sebesar 5% dengan asumsi
bahwa 5 dari 100 kesimpulan kita akan
menolak hipotesa yang seharusnya kita
terima atau kira-kira 95% konfiden bahwa kita
telah membuat kesimpulan yang benar

16. •Data Curah Hujan
Data curah hujan yang digunakan untuk
menghitung curah hujan rencana pada DAS Sungai
Bangga adalah data curah hujan hasil pengukuran
pada stasiun curah hujan Bangga Atas yang terletak
pada 1º17’14” LS dan 119º54’01” BT dan stasiun
Bangga Bawah yang terletak pada 1º14’35” LS dan
119º54’35” BT. Dari kedua data stasiun tersebut akan
ditentukan nilai curah hujan rata – rata daerah
maksimum, seperti terlihat pada tabel berikut
selama kurun waktu 10 tahun.
Contoh
Perhitungan

17. No. Tahun
Curah Hujan Maksimum (mm)
Bangga Atas Bangga Bawah
1 2000 57,90 81,30
2 2001 77,40 85,50
3 2002 89,20 94,90
4 2003 48,50 45,90
5 2004 69,80 65,00
6 2006 66,50 72,20
7 2007 78,80 87,10
8 2008 72,00 57,90
9 2009 98,00 50,00
10 2010 111,20 76,50
Data Curah Hujan Harian Maksimum Stasiun Curah
Hujan DAS Bangga
No. Tahun
Curah Hujan Maksimum (mm)
Bangga Atas Bangga Bawah
1 2000 57,90 81,30
2 2001 77,40 85,50
3 2002 89,20 94,90
4 2003 48,50 45,90
5 2004 69,80 65,00
6 2006 66,50 72,20
7 2007 78,80 87,10
8 2008 72,00 57,90
9 2009 98,00 50,00
10 2010 111,20 76,50
Sumber : Balai Wilayah Sungai Sulawesi III

18. Curah Hujan Maksimum dengan Rata – rata Hitung
No. Tahun Tanggal Bangga Atas Bangga Bawah Rata - rata Ekstrim
1 2000
20-Jan 57,90 7,50 32,70
41,10
21-Jan 0,90 81,30 41,10
2 2001
20-Apr 77,40 44,30 60,85
60,85
25-Jun 0,00 85,50 42,75
3 2002
11-Nov 89,20 40,00 64,60
64,60
19-Nov 5,80 94,90 50,35
4 2003
15-Okt 48,50 24,10 36,30
36,30
16-Apr 22,20 45,90 34,05
5 2004
7-Mei 69,80 0,00 34,90
34,90
9-Mei 2,00 65,00 33,50
6 2006
20-Juli 66,50 23,30 44,90
44,90
12-Apr 0,00 72,20 36,10
7 2007
4-Mei 78,80 47,10 62,95
62,95
23-Jan 8,10 87,10 47,60
8 2008 22-Juli 72,00 57,90 64,95 64,95
9 2009
27 -Agust 98,00 0,00 49,00
49,00
20-Mar 26,50 50,00 38,25
10 2010
10-Jun 111,20 15,30 63,25
77,95
21-Agust 79,40 76,50 77,95
Sumber : Hasil Perhitungan

19. No. Tahun Curah Hujan (Xi), mm
1 2010 77,95
2 2008 64,95
3 2002 64,60
4 2007 62,95
5 2001 60,85
6 2009 49,00
7 2006 44,90
8 2000 41,10
9 2003 36,30
10 2004 34,90
Data Curah Hujan Harian Maksimum Berdasarkan Rangking
No. Tahun Curah Hujan (Xi), mm
1 2010 77,95
2 2008 64,95
3 2002 64,60
4 2007 62,95
5 2001 60,85
6 2009 49,00
7 2006 44,90
8 2000 41,10
9 2003 36,30
10 2004 34,90
0
20
40
60
80
2000 2001 2002 2003 2004 2006 2007 2008 2009 2010
CurahHujan(mm)
Tahun
Curah Hujan Harian Maksimum DAS Bangga
Gambar 5.1. Grafik Curah Hujan Harian Maksimum DAS Bangga
Sumber :
Hasil
Perhitungan

20. •Uji Abnormalitas Data Curah Hujan
Pemeriksaan abnormalitas data dimaksudkan untuk memperkirakan
adanya curah hujan yang abnormal. Dalam uji abnormalitas data yang di
uji adalah data hujan maksimum dan minimum dan untuk sementara data
hujan maksimum dan minimum disingkirkan. Data hujan yang tersisa
diranking dari data terkecil ke data terbesar.
Ranking Xi Log Xi Xi + b Log (Xi + b) (Log (Xi + b))2
Data (mm) (mm) (mm) (mm) (mm)2
1 36,30 1,5599 36,3000 1,5599 2,4333
2 41,10 1,6138 41,1000 1,6138 2,6045
3 44,90 1,6522 44,9000 1,6522 2,7299
4 49,00 1,6902 49,0000 1,6902 2,8568
5 60,85 1,7843 60,8500 1,7843 3,1836
6 62,95 1,7990 62,9500 1,7990 3,2364
7 64,60 1,8102 64,6000 1,8102 3,2769
8 64,95 1,8126 64,9500 1,8126 3,2854
Jumlah 13,7223 13,7223 23,6068
Rata-rata 1,7153 1,7153 2,9509
Sumber : Hasil Perhitungan
Tabel. Uji
Abnormalitas Data
Curah Hujan

21. No.
R
Maksimum
(Xi - Xo)
(Xi -
Xo)2
(Xi - Xo)3 (Xi - Xo)4
1
77,95
22,1056 488,6556
10802,003
2
238784,282
1
2 64,95 9,1056 82,9111 754,9520 6874,2575
3 64,60 8,7556 76,6598 671,1987 5876,7177
4 62,95 7,1056 50,4889 358,7518 2549,1310
5 60,85 5,0056 25,0556 125,4171 627,7824
6 49,00 -6,8444 46,8464 -320,6377 2194,5870
7 44,90 -10,9444 119,7809 -1310,9350 14347,4554
8 41,10 -14,7444 217,3986 -3205,4222 47262,1695
9
36,30
-19,5444 381,9853 -7465,6906
145912,776
0
Jumlah 502,6000
0,0000
1489,782
2
409,6373
464429,158
8Rata-rata 55,8444
1.Pemilihan Agihan Frekuensi Metode Gumbell
Pemilihan Agihan Frekuensi
Menghitung parameter statistik Cs, Cv, Ck untuk menentukan pemilihan agihan
frekuensi. Syarat untuk EJ. Gumbell, Ck = 5,40 dan Cs = 1,14, Log Pearson III harga
Cs dan Cvnya bebas.
Perhitungan pemilihan agihan frekuensi dengan menggunakan metode
Gumbell, terlebih dahulu dicari nilai (Xi - Xo), (Xi - Xo)2, (Xi - Xo)3, dan (Xi
- Xo)4.
Tabel . Perhitungan Metode Gumbell
No. R Maksimum (Xi - Xo) (Xi - Xo)2 (Xi - Xo)3 (Xi - Xo)4
1 77,95 22,1056 488,6556 10802,0032 238784,2821
2 64,95 9,1056 82,9111 754,9520 6874,2575
3 64,60 8,7556 76,6598 671,1987 5876,7177
4 62,95 7,1056 50,4889 358,7518 2549,1310
5 60,85 5,0056 25,0556 125,4171 627,7824
6 49,00 -6,8444 46,8464 -320,6377 2194,5870
7 44,90 -10,9444 119,7809 -1310,9350 14347,4554
8 41,10 -14,7444 217,3986 -3205,4222 47262,1695
9 36,30 -19,5444 381,9853 -7465,6906 145912,7760
Jumlah 502,6000
0,0000 1489,7822 409,6373 464429,1588
Rata-rata 55,8444
Sumber :
Hasil
Perhitungan

22.  
1
1
2




n
XX
S
n
i
oi
x 19
7822,1489

 6463,13
•Menghitung simpangan baku
 
   3
1
3
21 x
n
i
oi
s
Snn
XX
C




   3
6463,132919
)6373,409(

 0028,0
•Menghitung parameter-parameter statistik, yang
meliputi koefisien skewnes/penyimpangan (Cs), koefisien
kurtosis (Ck) dan koefisien varians (Cv), dengan
persamaan :

23.  
    3
1
42
321 x
n
i
oi
k
Snnn
XXn
C




 
    3
2
6463,13392919
)1588,464429(9


0571,44
o
x
v
X
S
C 
8444,55
6463,13
 2444,0

24. 1. Analisis Frekuensi Metode Log Person III
Perhitungan analisis frekuensi dengan menggunakan metode Log
Person III terlebih dahulu dicari nilai (Log Xi – Log X), (Log Xi – Log
X)2, (Log Xi – Log X)3, dan (Log Xi – Log X)4.
No.
R
Max
(mm)
Log Xi
(LogXi -
LogX)
(LogXi - LogX)2 (LogXi - LogX)3 (LogXi - LogX)4
1 77,95 1,8918 0,156919 0,024624 0,003864 0,000606
2 64,95 1,8126 0,077682 0,006034 0,000469 0,000036
3 64,60 1,8102 0,075335 0,005675 0,000428 0,000032
4 62,95 1,7990 0,064099 0,004109 0,000263 0,000017
5 60,85 1,7843 0,049363 0,002437 0,000120 0,000006
6
49,00 1,6902
-
0,044701 0,001998 -0,000089 0,000004
7
44,90 1,6522
-
0,082651 0,006831 -0,000565 0,000047
8
41,10 1,6138
-
0,121055 0,014654 -0,001774 0,000215
9
36,30 1,5599
-
0,174991 0,030622 -0,005359 0,000938
Jumlah 15,6141 0,000000 0,096984 -0,002643 0,001901
Log Xo 1,7349 0,000000 0,010776 -0,000294 0,000211
Sumber : Hasil
Perhitungan
Perhitungan
Metode Log
Person III

25.  
1n
xlogxlog
n
1i
2
oi


19
096984,0

•Menghitung standar deviasi
S log x =
= 0,1101

26. Menghitung parameter-parameter statistik, yang meliputi koefisien
skewnes/penyimpangan (Cs), koefisien kurtosis (Ck) dan koefisien varians (Cv), dengan
persamaan :
Berdasarkan harga
Cs, Ck dan Cv maka
analisis frekuensi
yang paling sesuai
dan memenuhi
syarat adalah
analisis frekuensi
Log person III.

27. Periode
Ulang (T)
KTr Log Xo
Logaritma
Hujan
Rancangan
Hujan
Rancangan,
XT
2 0,0060 1,7349 1,7356 54,3950
5 0,8399 1,7349 1,8274 67,2004
10 1,2778 1,7349 1,8756 75,0904
25 1,7386 1,7349 1,9263 84,3972
50 2,0349 1,7349 1,9590 90,9809
100 2,2998 1,7349 1,9881 97,3016
Untuk mendapatkan harga XT (Hujan Rancangan), maka harga KTr
diberi nilai sesuai dengan harga Cs (koefisien skewness) dan kala
ulang, dari harga-harga tersebut dapat ditarik suatu garis lurus.
•Untuk kala ulang 2 tahun
Untuk kala ulang 2 tahun dan Cs = -0,0354 dari tabel faktor
penyimpangan KTr untuk Log Pearson III diperoleh nilai harga KTr =
0,0060, sehingga :
Log XT = Log Xo + KTr . S Log X
= 1,7349 + (0,0060 x 0,1101)
= 1,7356
XT = 10 1,7356
= 54,3950 mm

28. •Untuk kala ulang 100 tahun
Untuk kala ulang 100 tahun dan Cs = -0,0354 dari tabel 3.9.
faktor penyimpangan KTr untuk Log Pearson III diperoleh
nilai harga KTr = 2,2998, sehingga :
Log XT = Log Xo + KTr . S Log X
= 1,7349 + (2,2998 x 0,1101)
= 1,9881
XT = 10 1,9881
= 97,3016 mm

29. Periode
Ulang (T)
KTr Log Xo
Logaritma
Hujan
Rancangan
Hujan
Rancangan,
XT
2 0,0060 1,7349 1,7356 54,3950
5 0,8399 1,7349 1,8274 67,2004
10 1,2778 1,7349 1,8756 75,0904
25 1,7386 1,7349 1,9263 84,3972
50 2,0349 1,7349 1,9590 90,9809
100 2,2998 1,7349 1,9881 97,3016
Sumber : Hasil Perhitungan
Perhitungan Curah Hujan Rancangan
Distribusi Log Pearson III

30. Hasil dari metode distribusi Log Person III harus diuji
validitas terlebih dahulu sebelum digunakan dalam
perhitungan debit banjir rencana. Uji ini berupa Chi
Square Test dan uji Smirnov Kolmogorof Test.
 1
.100
n
m
 19
1.100
 10
•Uji Kesesuaian Distribusi Frekuensi
Setelah diketahui analisis frekuensinya maka sebaran data yang
dipilih yaitu uji dengan Chi Square Test dan uji Smirnov Kolmogorof
Test. Untuk itu sebelumnya dilakukan perhitungan peluang dengan
menggunakan metode Weibull.
dengan :
P = peluang (%)
m = nomor urut data
n = banyaknya data
P = =

31. No. Curah hujan (mm) Peluang (P) (%)
1 36,30 10,00
2 41,10 20,00
3 44,90 30,00
4 49,00 40,00
5 60,85 50,00
6 62,95 60,00
7 64,60 70,00
8 64,95 80,00
9 77,95 90,00
Perhitungan Peluang Metode Weibull
No. Curah hujan (mm) Peluang (P) (%)
1 36,30 10,00
2 41,10 20,00
3 44,90 30,00
4 49,00 40,00
5 60,85 50,00
6 62,95 60,00
7 64,60 70,00
8 64,95 80,00
9 77,95 90,00
Sumber : Hasil Perhitungan

32. Nilai Batas Sub
Kelompok
Jumlah Data
Ef - Of
Ef Of
0 ≤ P ≤ 11,25 1,125 1 0,125 0,01563
11,25 < P ≤ 22,50 1,125 1 0,125 0,01563
22,50 < P ≤ 33,75 1,125 1 0,125 0,01563
33,75 < P ≤ 45 1,125 1 0,125 0,01563
45 < P ≤ 56,25 1,125 1 0,125 0,01563
56,25 < P ≤ 67,5 1,125 1 0,125 0,01563
67,50 < P ≤ 78,75 1,125 1 0,125 0,01563
78,75 < P ≤ 90 1,125 2 0,875 0,76563
Jumlah 9 9 0,8750

33. Nilai Batas Sub
Kelompok
Jumlah Data
Ef - Of
Ef Of
0 ≤ P ≤ 11,25 1,125 1 0,125 0,01563
11,25 < P ≤ 22,50 1,125 1 0,125 0,01563
22,50 < P ≤ 33,75 1,125 1 0,125 0,01563
33,75 < P ≤ 45 1,125 1 0,125 0,01563
45 < P ≤ 56,25 1,125 1 0,125 0,01563
56,25 < P ≤ 67,5 1,125 1 0,125 0,01563
67,50 < P ≤ 78,75 1,125 1 0,125 0,01563
78,75 < P ≤ 90 1,125 2 0,875 0,76563
Jumlah 9 9 0,8750
Perhitungan Uji Chi Square
Sumber : Hasil perhitungan

34. y = 17,78ln(x) + 30,55
R² = 0,878
10
100
1000
1 10 100 1000
CurahHujan(mm)
Probabilitas (%)
Uji Kecocokan Metode Chi Square
Gambar 5.2. Uji Kesesuaian Distribusi Frekuensi Metode Chi Square

35. Sehingga kesimpulannya :
- X2 hitung < X2 Cr
- 0,7777 < 9,236
Berdasarkan distribusi data tersebut maka distribusi
frekuensi dapat diterima dengan menggunakan
distribusi frekuensi Log Person III.

36. No.
Curah
Hujan
(mm)
P.
Distribu
si
Empiris
(%)
P.
Distribus
i Teoritis
(%)
Pe - Pt | Pe - Pt |
(%) (%)
1 77,95 10,00 13 -3,00 3,00
2 64,95 20,00 32 -12,00 12,00
3 64,60 30,00 33 -3,00 3,00
4 62,95 40,00 35 5,00 5,00
5 60,85 50,00 39 11,00 11,00
6 49,00 60,00 61 -1,00 1,00
7 44,90 70,00 71 -1,00 1,00
8 41,10 80,00 80 0,00 0,00
9 36,30 90,00 93 -3,00 3,00
•Smirnov Kolmogorov Test
Pengujian ini dilakukan dengan mencari nilai selisih probabilitas tiap varian, menurut distribusi
empiris dan teoritis yaitu disimbolkan dengan Δ. Harga Δ maksimum harus lebih kecil dari Δ
kritis. Hasil pengujian untuk kasus ini dapat dilihat pada tabel berikut :
Tabel 5.11. Perhitungan Uji Smirnov Kolmogorov
No.
Curah
Hujan (mm)
P.
Distrib
usi
Empiris
(%)
P.
Distribu
si
Teoritis
(%)
Pe - Pt | Pe - Pt |
(%) (%)
1 77,95 10,00 13 -3,00 3,00
2 64,95 20,00 32 -12,00 12,00
3 64,60 30,00 33 -3,00 3,00
4 62,95 40,00 35 5,00 5,00
5 60,85 50,00 39 11,00 11,00
6 49,00 60,00 61 -1,00 1,00
7 44,90 70,00 71 -1,00 1,00
8 41,10 80,00 80 0,00 0,00
9 36,30 90,00 93 -3,00 3,00
Sumber : Hasil perhitungan
y = -105,ln(x) + 470,1
R² = 0,947
1
10
100
1,000
10 100 1000
Probabilitas(%)
Curah Hujan (mm)
Uji Kecocokan Metode Smirnov
Kolmogorov
Gambar 5.3. Uji Kesesuaian Distribusi Frekuensi Metode Smirnov Kolm

38. S e k i a n
&
T e r i m a K a s i h
Created by :
Dian Wahyuni Werokila,
ST/