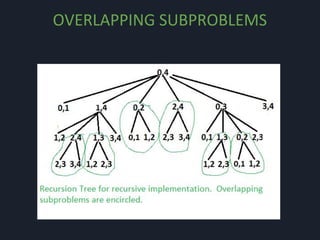
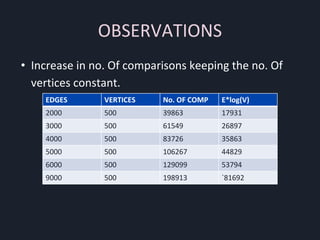
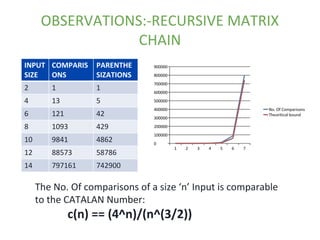
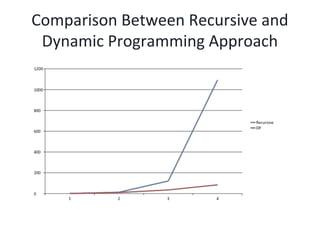
The presentation summarizes algorithms topics including dynamic programming, greedy algorithms, and sorting. It covers dynamic programming approaches to matrix chain multiplication and polygon triangulation. It also discusses the recursive and memoized solutions to matrix chain multiplication, and compares their time complexities. Kruskal's minimum spanning tree algorithm is explained along with observations on its runtime with increasing edges or vertices. Quicksort is analyzed using least squares fitting to determine constants in its average time complexity formula.

1. ALGORITHMS II LAB
PRESENTATION
Presented By:-
Rishabh Kumar Sharma, Gx-05
Aman Prasad, Gx-07
Abhishek Chandra, Gx-25
Debtanu Pal, Gx-24
IIEST SHIBPUR

2. CONTENTS
• Assignment on Dynamic Programming
– Matrix Chain Multiplication
• Naive Recursive Approach
• Dynamic Programming Approach
• Memoized Matrix Chain
• Comparison between the 2 approaches
• Extension of the Dynamic Programming Approach for
Matrix Multiplication to Polygon Triangulation

3. CONTENTS
• Assignment on Greedy Algorithms
– Huffman Compression Algorithm
● Study variation of average codeword length with change
in the probability of occurrence of a symbol

4. DYNAMIC PROGRAMMING
• A Dynamic Programming Approach to a problem is taken
when a problem has the following 2 properties:-
– Optimal Substructure :- Optimal Solution to a problem
includes within it the optimal solution to a subproblem.
– Overlapping Subproblems

5. RECURSIVE MATRIX CHAIN
RMC(p,i,j)
if i==j then return zero
m[i,j]=INF
for k=i to j-1
q=RMC(p,i,k)+RMC(p,k+1,j)+p(i-1)*p(k)*p(j)
if q<m[i,j]
m[i,j]=q
Return m[i,j]
Time Complexity of running this one:
T(n) ≥ 1+∑(T(k)+T(n-k)+1) ≥ 2 ∑ T(i) +n ≥ 2^n - 1

6. OBSERVATIONS:-RECURSIVE MATRIX
CHAIN
INPUT
SIZE
COMPARIS
ONS
PARENTHE
SIZATIONS
2 1 1
4 13 5
6 121 42
8 1093 429
10 9841 4862
12 88573 58786
14 797161 742900
The No. Of comparisons of a size ‘n’ Input is comparable
to the CATALAN Number:
c(n) == (4^n)/(n^(3/2))

7. REASON
We have to check each and every possible parenthesization
and hence solve a large no. Of problems repeatedly.

8. MATRIX CHAIN MUL. USING DP
MATRIX-CHAIN-ORDER (p)
n=length[p]-1
for i=1 to n
m[i,i]=0
for l=2 to n
for i=1 to n-l+1
j=i+l-1
m[i,j]=INF
for k=i to j-1
q=m[i,k]+m[k+1,j]+pi-1pkpj
if q< m[i,j]
m[i,j]=q ; s[i,j]=k
Return m and s

9. HISTOGRAM COMPARISON
MATRIX CHAIN MULTIPLICATION
USING BRUTE FORCE APPROACH
MATRIX CHAIN MULTIPLICATION
USING DP

10. Comparison Between Recursive and
Dynamic Programming Approach

11. MATRIX CHAIN MULTIPLICATION USING
MEMOIZATION
Mem-Matrix-Chain(array p, int i, int j) {
if (m[i, j] != UNDEFINED) then
return m[i, j]; // already defined
else if ( i = = j) then
m[i, i] = 0; // basic case
else {
m[i, j] = infinity; // initialize
for k = i to j − 1 do {// try all splits
cost = Mem-Matrix-Chain(p,i,k) +
Mem-Matrix-Chain(p,k+1,j)+ p[i−1]p[k]p[j];
if (cost < m[i, j]) then // update if better
m[i, j] = cost;
}
}
return m[i, j]; // return final cost
}

12. POLYGON TRIANGULATION COMPARISON
WITH MATRIX CHAIN MULTIPLICATION
MATRIX CHAIN MULTIPLICATION
• Problem involves finding the
optimal parenthesization so that
no. Of multiplications is
minimum.
• Optimal Substructure –
Subproblems consist of finding
minimum no. Of multiplication of
the smaller subchains
• Bottom up approach consists of a
table in which we keep record of
the particular parenthesization
for which the multiplication is
minimum.
POLYGON TRIANGULATION
• Problem involves finding the optimal
triangulation so that the perimeter
of the resulting triangulation is
minimum.
• Optimal Substructure- Subproblems
consist of finding minimum cost
subpolygons on the left and right
side of the first triangulation.
• Bottom up approach consists of a
table which keeps records of the
smaller polygons(and the minimum
perimeter to triangulate these)

13. ALGORITHM
for (int gap = 0; gap < n; gap++)
for (int i = 0, j = gap; j < n; i++, j++)
if (j < i+2){
table[i][j] = 0 ;
//INITIALIZATION OF THE TABLE TO STORE MINIMAL TRIANGULATION COST
tri[i][j]=0;
}
else{
table[i][j] = MAX;
for (int k = i+1; k < j; k++){
double val = table[i][k] + table[k][j] + cost(points,i,j,k);
//CALCULATING THE COST OF THE GIVEN TRIANGULATION
if (table[i][j] > val) {
// COMPARING WITH THE VALUES IN TABLE TO FIND MINIMAL TRIANGULATION
table[i][j] = val;
tri[i][j]=k;
} c++;
}
return table[0][n-1];

14. OVERLAPPING SUBPROBLEMS

15. A SMALL EXAMPLE
OPTIMAL
TRIANGULATION:
COST – 15.30
ANOTHER
TRIANGULATION:
COST – 15.77

16. KRUSKAL'S ALGORITHM
• 1. Sort all the edges in non-decreasing order of their weight.
• 2. Pick the smallest edge. Check if it forms a cycle with the spanning tree
formed so far. If cycle is not formed, include this edge. Else, discard it. //
GREEDY ELEMENT
• 3. To check the existence of cycle, check whether for two vertices x and
y. Find_set(x)==Find_set(y), or not. If equal they already belong to the
same disjoint set(tree), hence will form a cycle if they are joined. So
edge(x,y) will not belong to the MST. // DISJOINT SETS
• 4. Repeat step 2 until there are (V-1) edges in the spanning tree.

17. TIME COMPLEXITY
• Time Complexity: O(ElogE) or O(ElogV).
• Sorting of edges takes O(ELogE) time.
• After sorting, we iterate through all edges and apply
find-union algorithm.
• The find and union operations can take atmost O(LogV) time.
• So overall complexity is O(ELogE + ELogV) time.
• The value of E can be atmost O(V2
), so O(LogV) are O(LogE)
same.
• Therefore, overall time complexity is O(ElogE) or O(ElogV)

18. OBSERVATIONS
• Increase in no. Of comparisons keeping the no. Of
vertices constant.
EDGES VERTICES No. OF COMP E*log(V)
2000 500 39863 17931
3000 500 61549 26897
4000 500 83726 35863
5000 500 106267 44829
6000 500 129099 53794
9000 500 198913 `81692

19. Graphical Representation
X-axis: Input number Y-axis: No. Of Comparisons

20. OBSERVATIONS
• Increase in no. Of comparisons keeping the
no. Of vertices constant.
EDGES VERTICES COMP
5000 500 106267
5000 600 107582
5000 700 108694
5000 800 109657
5000 900 111267

21. Graphical Representation

22. COMPARISON
EDGES INC. VERTICES CONST. VERTICES INC. EDGES CONST.

23. COMPARISON
EDGES INC. VERTICES CONST.
EDGES VERTICES COMP.
5000 500 106267
5100 500 108539
5200 500 110812
5300 500 114089
VERTICES CONST. EDGES INC.
EDGES VERTICES COMP.
5000 500 106267
5000 600 107583
5000 700 108695
5000 800 109658

24. VALUE OF c and n0.... QUICKSORT
ASSIGNMENT
• We have the no. Of comparisons(yi) and the corresponding
input size(xi).
• Fit these points to the curve f(x)=axlogx +bx +c.
• Use the method of least squares.
• R^2 = (yi-f(xi))^2.
• Take Partial derivative of R^2 w.r.t a,b and c... And equate to
0.
• We get 3 variables and 3 equations.
• Finally, a=1.792, b= -7.48, c=79.8962.