Dokumen tersebut membahas metode-metode untuk menentukan akar persamaan non linier seperti metode pengurung, metode Newton-Raphson, dan metode secant. Metode-metode tersebut memanfaatkan konsep turunan dan nilai awal untuk memperoleh aproksimasi akar yang semakin mendekati nilai sesungguhnya.

1. Akar-akar Persamaan Non Linier
Diketahui fungsi kontinyu y = f(x)
Akar-akar persamaan adalah nilai x yang menyebabkan fungsi f(x)=0.
Jadi untuk mencari akar-akar suatu persamaan adalah dengan
menyelesaikan persamaan
f(x) = 0
untuk x.
y
y = f(x)
akar
0
x
xR

2. Metode numerik yang biasa digunakan untuk menentukan
akar-akar persamaan non linier adalah :
1. Metode Pengurung (bracket method)
Metode yang memanfaatkan suatu kenyataan bahwa harga fungsi akan
berubah tanda disekitar akar. Proses pencarian akar dimulai dengan
dua terkaan awal yang mengurung akar sebagai batas bawah dan batas atas.
- Metode Bagidua (bisection method)
- Metode Posisi Palsu (false position method)
2. Metode Terbuka
Diperlukan satu atau dua terkaan awal yang tidak perlu mengurung akar.
ada kemungkinan pencarian akar divergen, tapi jika konvergen
laju konvergensinya lebih cepat.
- Metode Newton-Raphson
- Metode Secant

3. Metode Bagidua (bisection method)
XR
XL
f(xU)
XU
2
Akar
xR
xL
xU
f(xL)
xR
xL
xU
xL
xU
xR

4. Metode Posisi Palsu (false position)
f(xU)
Dari hubungan segitiga sebangun
XL-f(XL)-XR dan XR-f(XU)-XU,
bisa ditulis
f (X L)
XR XL
xR
xU
xL
f ( XU )
X R XU
Akar
f(xU)
f(xL)
XR
xR
xU
xL
f(xL)
Akar
XU
( X L XU )
f ( XU )
f ( X L ) f ( XU )

5. Metode Langsung (Iterasi Satu Titik Sederhana)
Dengan menyusun kembali fungsi f(x) = 0 sedemikian sehingga
x berada diruas kiri persamaan, yaitu x = g(x). atau
dalam bentuk persamaan iterasi,
xi+1 = g(xi)
misal:
x2 - 2x + 3 = 0 
sin(x) = 0

x = (x2 + 3)/2
x = xin(x) + x
Kesalahan relatif persen aproksimasi ea:
ea
xi
xi
1
xi
*100%
1
Contoh-1: Gunakan metode langsung untuk menentukan akar persamaan
f(x) = e-x - x
mulai dengan terkaan awal x0 = 0

6. Intepretasi grafis Metode Langsung
f(x) = e-x - x
akar
akar
y1(x) = x
y2(x) = e-x

7. Konvergensi Metode Langsung
y1(x) = x
y1(x) = x
y2(x) = g(x)
y2(x) = g(x)
A (konvergen)
y2(x) = g(x)
C (divergen)
y1(x) = x
B (konvergen)
y2(x) = g(x)
y1(x) = x
D (divergen)

8. Metode Newton Raphson
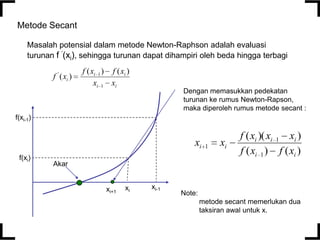
Jika terkaan awal pada akar adalah xi, maka sebuah garis singgung
dapat ditarik dari titik [xi, f(xi)]. Titik dimana garis singgung ini memotong
sumbu X biasanya menyatakan terkaan akar yang lebih baik.
Turunan pertama di xi, setara
dengan kemiringan, sehingga
bisa ditulis :
Kemiringan = f ’(xi)
f(xi)
f(xi) - 0
Akar
xi+1
atau
xi
xi – xi+1
f ( xi )
xi xi 1
f ' ( xi )
xi
1
xi
f ( xi )
f ' ( xi )

9. Metode Secant
Masalah potensial dalam metode Newton-Raphson adalah evaluasi
turunan f ’(xi), sehingga turunan dapat dihampiri oleh beda hingga terbagi
f ' ( xi )
f ( xi 1 ) f ( xi )
xi 1 xi
Dengan memasukkan pedekatan
turunan ke rumus Newton-Rapson,
maka diperoleh rumus metode secant :
f(xi-1)
xi
f(xi)
1
xi
f ( xi )( xi 1 xi )
f ( xi 1 ) f ( xi )
Akar
xi+1
xi
xi-1
Note:
metode secant memerlukan dua
taksiran awal untuk x.

10. Persamaan Polinom derajat n
P( x)
a0
a1 x a2 x 2 ... an x n
Polinom derajat n mempunyai TEPAT n akar, yaitu
• akar real (positif / negatif)
• akar komplek (berpasanga a + bi dan a – bi)
• akar yang mempunyai multiplisitas r, dihitung r kali
Cara Menentukan Banyaknya Akar dengan Aturan Descartes
1. Menentukan Akar Real Positif :
V = banyaknya pergantian tanda koefisien ai pada P(x)
Np = banyaknya akar real positif
V – Np = 0, 2, 4, . . .
2. Menentukan Akar Real Negatif :
V = banyaknya pergantian tanda koefisien ai pada P(-x)
Ng = banyaknya akar real negatif
V – Ng = 0, 2, 4, . . .
3. Menentukan batas-batas akar real positif/negatif
R = 1 + max |ai/an| , i = 0,1,2…n-1
akar P(x) terletak pada -R < x <R