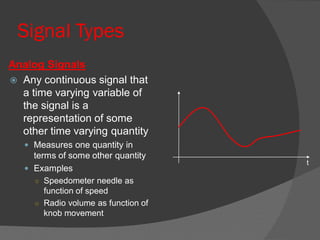
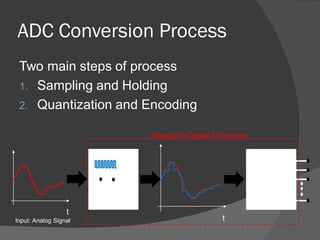
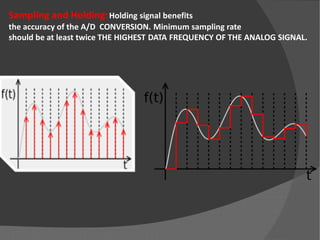
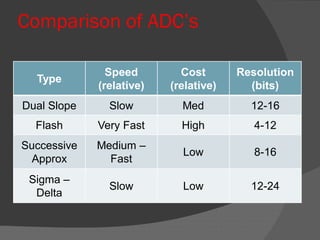
The document explains the function and processes of an Analog-to-Digital Converter (ADC), which transforms analog signals into digital form for processing. It outlines the key steps in ADC conversion: sampling and holding, as well as quantization and encoding, while addressing potential errors such as aliasing and quantization error. ADCs are essential in various applications, including microphones and digital multimeters, and their specifications are compared based on speed, cost, and resolution.

2.  What is ADC?
 Conversion Process
 Accuracy
 Examples of ADC applications

3. Signal Types
Analog Signals
 Any continuous signal that
a time varying variable of
the signal is a
representation of some
other time varying quantity
 Measures one quantity in
terms of some other quantity
 Examples
○ Speedometer needle as
function of speed
○ Radio volume as function of
knob movement
t

4. Signal Types
Digital Signals
 Consist of only two
states
 Binary States
 On and off
 Computers can only
perform processing on
digitized signals
0
1

5. Analog-Digital Converter (ADC)
 An electronic integrated circuit which
converts a signal from analog
(continuous) to digital (discrete) form
 Provides a link between the analog
world of transducers and the digital
world of signal processing and data
handling

6. ADC Conversion Process
Two main steps of process
1. Sampling and Holding
2. Quantization and Encoding
t
tInput: Analog Signal
Sampling and
Hold
Quantizing
and
Encoding
Analog-to-Digital Converter

7. Sampling and Holding:Holding signal benefits
the accuracy of the A/D CONVERSION. Minimum sampling rate
should be at least twice THE HIGHEST DATA FREQUENCY OF THE ANALOG SIGNAL.

8. QUANTIZING AND
ENCODING
RESOLUTION:
THE SMALLEST CHANGE IN ANALOG SIGNAL THAT WILL RESULT IN
A CHANGE IN
THE DIGITAL OUTPUT.
V = REFERENCE VOLTAGE RANGE
N = NUMBER OF BITS IN DIGITAL OUTPUT.
2N = NUMBER OF STATES.
∆V = RESOLUTION
THE RESOLUTION REPRESENTS THE QUANTIZATION ERROR
INHERENT IN THE
CONVERSION OF THE SIGNAL TO DIGITAL FORM

9. • QUANTIZING:
PARTITIONING THE
REFERENCE SIGNAL RANGE
INTO A NUMBER OF
DISCRETE QUANTA,
THEN MATCHING THE
INPUT SIGNAL TO THE
CORRECT QUANTUM.
• ENCODING:
ASSIGNING A UNIQUE DIGITAL
CODE TO EACH
QUANTUM, THEN
ALLOCATING THE
DIGITAL CODE TO THE
INPUT

10. ADC-Error Possibilities
Aliasing (sampling)
 Occurs when the input signal is changing much
faster than the sample rate
 Should follow the Nyquist Rule when sampling
○ Answers question of what sample rate is required
○ Use a sampling frequency at least twice as high as the
maximum frequency in the signal to avoid aliasing
○ fsample>2*fsignal
Quantization Error (resolution)
 Optimize resolution
 Dependent on ADC converter of microcontoller

11. ADC Applications
 ADC are used virtually everywhere
where an analog signal has to be
processed, stored, or transported in
digital form
 Microphones
 Strain Gages
 Thermocouple
 Digital Multimeters

12. Comparison of ADC’s
Type
Speed
(relative)
Cost
(relative)
Resolution
(bits)
Dual Slope Slow Med 12-16
Flash Very Fast High 4-12
Successive
Approx
Medium –
Fast
Low 8-16
Sigma –
Delta
Slow Low 12-24

13. ADC Subsystem of MC9S12C32
Input Pins
ADC Built-into
MC9S12C32
Presenter: Ehsan Maleki