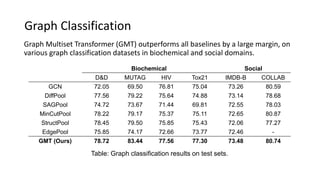
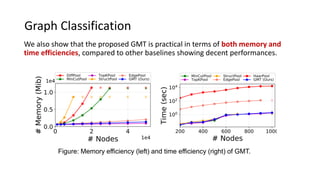
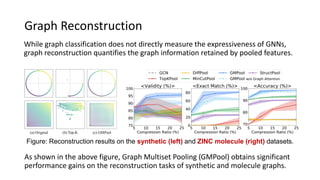
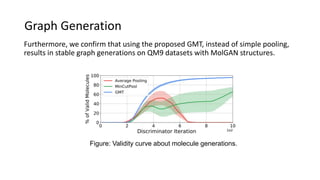
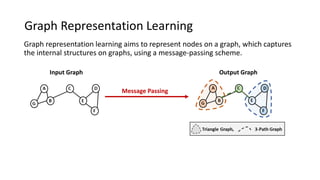
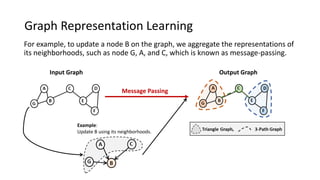
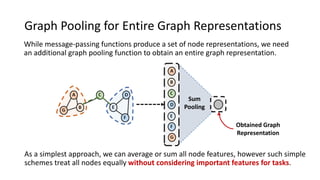
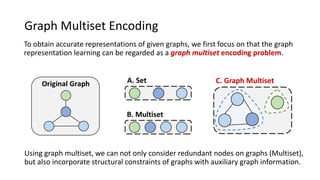
This paper presents a novel graph representation learning approach utilizing graph multiset pooling to effectively encode graphs by considering structural constraints and node interactions. The proposed graph multiset transformer (GMT) model demonstrates substantial performance improvements in graph classification, reconstruction, and generation tasks compared to existing methods, while also showcasing efficiency in memory and time usage. The findings suggest that the GMT can reach the expressive power of the Weisfeiler-Lehman test, paving the way for enhanced graph analysis techniques.

1. Accurate Learning of Graph Representations
with Graph Multiset Pooling
Jinheon Baek1*, Minki Kang1*, Sung Ju Hwang1,2
(*: equal contribution)
1Graduate School of AI, KAIST, South Korea
2AITRICS, South Korea

2. Graph Representation Learning
Graph representation learning aims to represent nodes on a graph, which captures
the internal structures on graphs, using a message-passing scheme.
Input Graph Output Graph
Message Passing

3. Graph Representation Learning
For example, to update a node B on the graph, we aggregate the representations of
its neighborhoods, such as node G, A, and C, which is known as message-passing.
Input Graph Output Graph
Message Passing
Example:
Update B using its neighborhoods.

4. Graph Pooling for Entire Graph Representations
As a simplest approach, we can average or sum all node features, however such simple
schemes treat all nodes equally without considering important features for tasks.
While message-passing functions produce a set of node representations, we need
an additional graph pooling function to obtain an entire graph representation.
Obtained Graph
Representation
Sum
Pooling

5. Graph Multiset Encoding
Using graph multiset, we can not only consider redundant nodes on graphs (Multiset),
but also incorporate structural constraints of graphs with auxiliary graph information.
To obtain accurate representations of given graphs, we first focus on that the graph
representation learning can be regarded as a graph multiset encoding problem.
A. Set
B. Multiset
C. Graph Multiset

6. Graph Multiset Pooling
Given a graph with node features, we define a Graph Multiset Pooling (GMPool)
to compress many nodes into few typical nodes, using a graph multiset scheme.
Input Graph
Message
Passing
Triangle Graph, 3-Path Graph
Node Space that
reflects graph structures
Seed Vectors 𝑺
GMPool
E
A
B
C D
F
G
E
A
B
C D
F
G
C
E
D
F
A
B
G
Graph
Attention

7. Graph Multiset Transformer
To further consider the interactions among 𝑛 or condensed 𝑘 different nodes,
we propose a Self-Attention function (SelfAtt), inspired by Transformer [1].
[1] Vaswani et al. Attention Is All You Need. NIPS 2017.
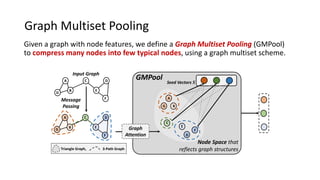
Notably, the full structure of our model, namely Graph Multiset Transformer (GMT),
consists of GMPool for compressing nodes, and SelfAtt for considering interactions.

8. Connection with Weisfeiler-Lehman (WL) Test
Weisfeiler-Lehman (WL) test is known for its ability to distinguish two different
graphs, and our overall architecture can be at most as powerful as the WL test:
Please see the Theorem 1, Lemma 2, and Proposition 3 in section 3.3 of main paper.
• Theorem 1 (Non-isomorphic Graphs to Different Embeddings).
• Lemma 2 (Uniqueness on Graph Multiset Pooling).
• Proposition 3 (Injectiveness on Pooling Function).

9. Connection with Node Clustering
While the proposed Graph Multiset Pooling needs a linear space 𝑶(𝒏) for 𝑛 nodes,
it can be further approximated to the node clustering approach with 𝑘 clusters:
Please see the Theorem 4, and Proposition 5 in section 3.4 of main paper.
• Theorem 4 (Space Complexity of Graph Multiset Pooling).
• Proposition 5 (Approximation to Node Clustering).

10. Experiments
We validate the proposed Graph Multiset Pooling on graph classification,
reconstruction, and generation tasks of synthetic and real-world graphs.
• Graph Classification
: The goal is to predict a label of a given graph.
• Graph Reconstruction
: The goal is to reconstruct the node features of graphs from their pooled representations.
• Graph Generation
: The goal is to generate a valid graph with desired properties.

11. Graph Classification
Graph Multiset Transformer (GMT) outperforms all baselines by a large margin, on
various graph classification datasets in biochemical and social domains.
Biochemical Social
D&D MUTAG HIV Tox21 IMDB-B COLLAB
GCN 72.05 69.50 76.81 75.04 73.26 80.59
DiffPool 77.56 79.22 75.64 74.88 73.14 78.68
SAGPool 74.72 73.67 71.44 69.81 72.55 78.03
MinCutPool 78.22 79.17 75.37 75.11 72.65 80.87
StructPool 78.45 79.50 75.85 75.43 72.06 77.27
EdgePool 75.85 74.17 72.66 73.77 72.46 -
GMT (Ours) 78.72 83.44 77.56 77.30 73.48 80.74
Table: Graph classification results on test sets.

12. Graph Classification
We also show that the proposed GMT is practical in terms of both memory and
time efficiencies, compared to other baselines showing decent performances.
Figure: Memory efficiency (left) and time efficiency (right) of GMT.

13. Graph Reconstruction
While graph classification does not directly measure the expressiveness of GNNs,
graph reconstruction quantifies the graph information retained by pooled features.
As shown in the above figure, Graph Multiset Pooling (GMPool) obtains significant
performance gains on the reconstruction tasks of synthetic and molecule graphs.
Figure: Reconstruction results on the synthetic (left) and ZINC molecule (right) datasets.

14. Graph Generation
Furthermore, we confirm that using the proposed GMT, instead of simple pooling,
results in stable graph generations on QM9 datasets with MolGAN structures.
Figure: Validity curve about molecule generations.

15. Conclusion
• We treat a graph pooling problem as a graph multiset encoding problem, under
which we consider relationships among nodes with several attention units.
• We show that existing GNNs with the proposed pooling can be as powerful as
the WL test, and also be extended to the node clustering approaches.
• We validate GMT for graph classification, reconstruction, and generation tasks
on synthetic and real-world graphs, on which it largely outperforms baselines.