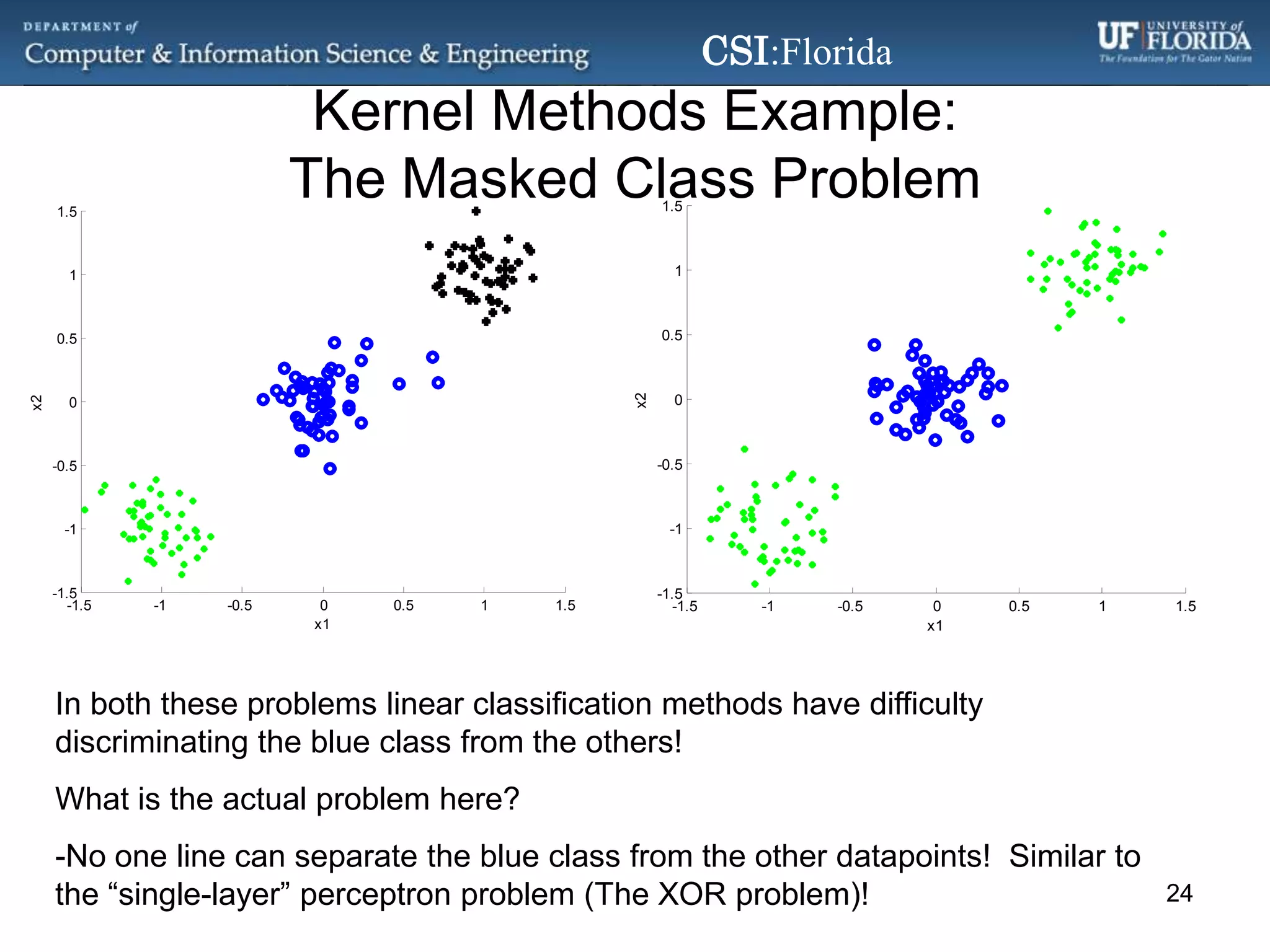
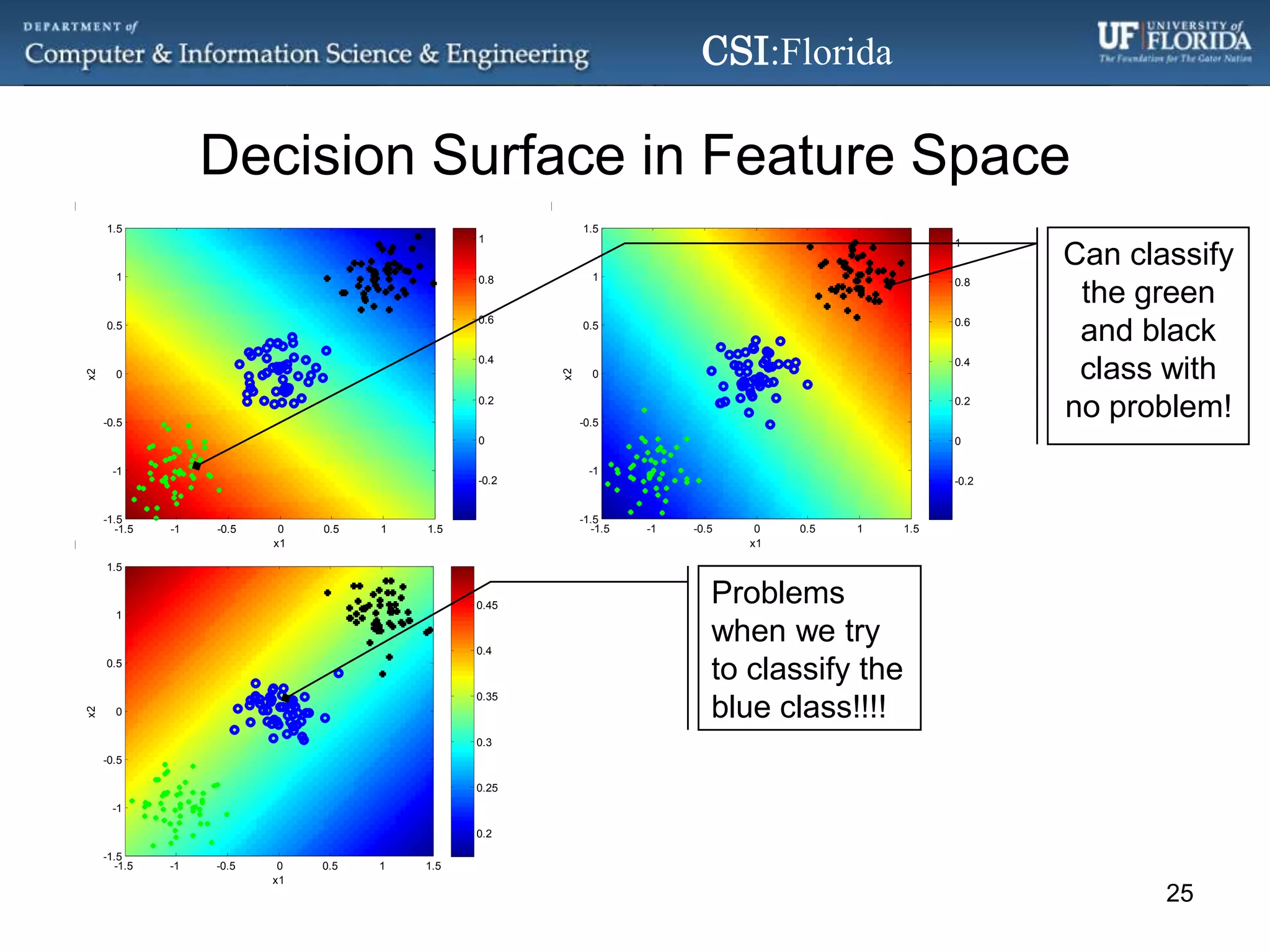
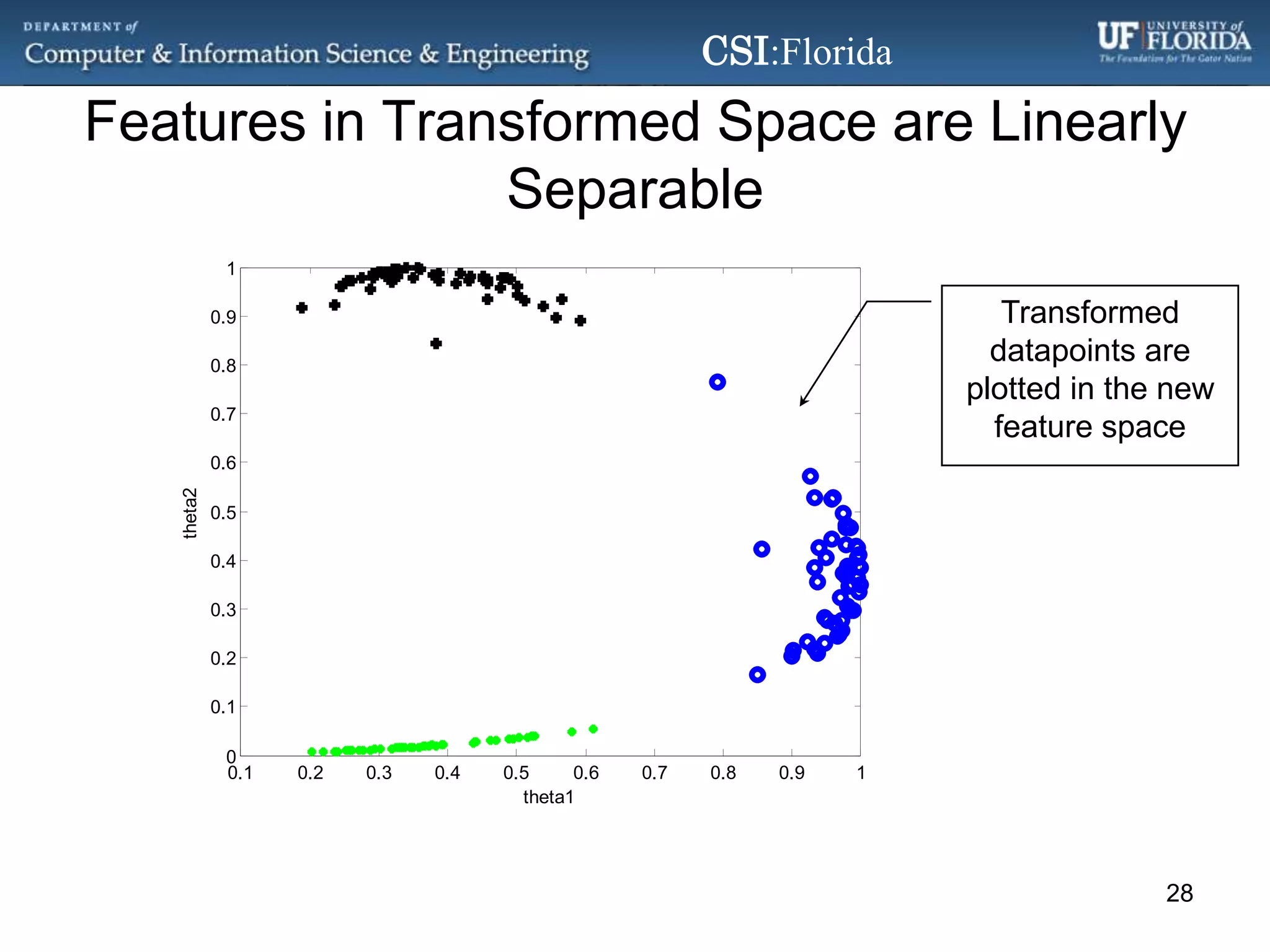
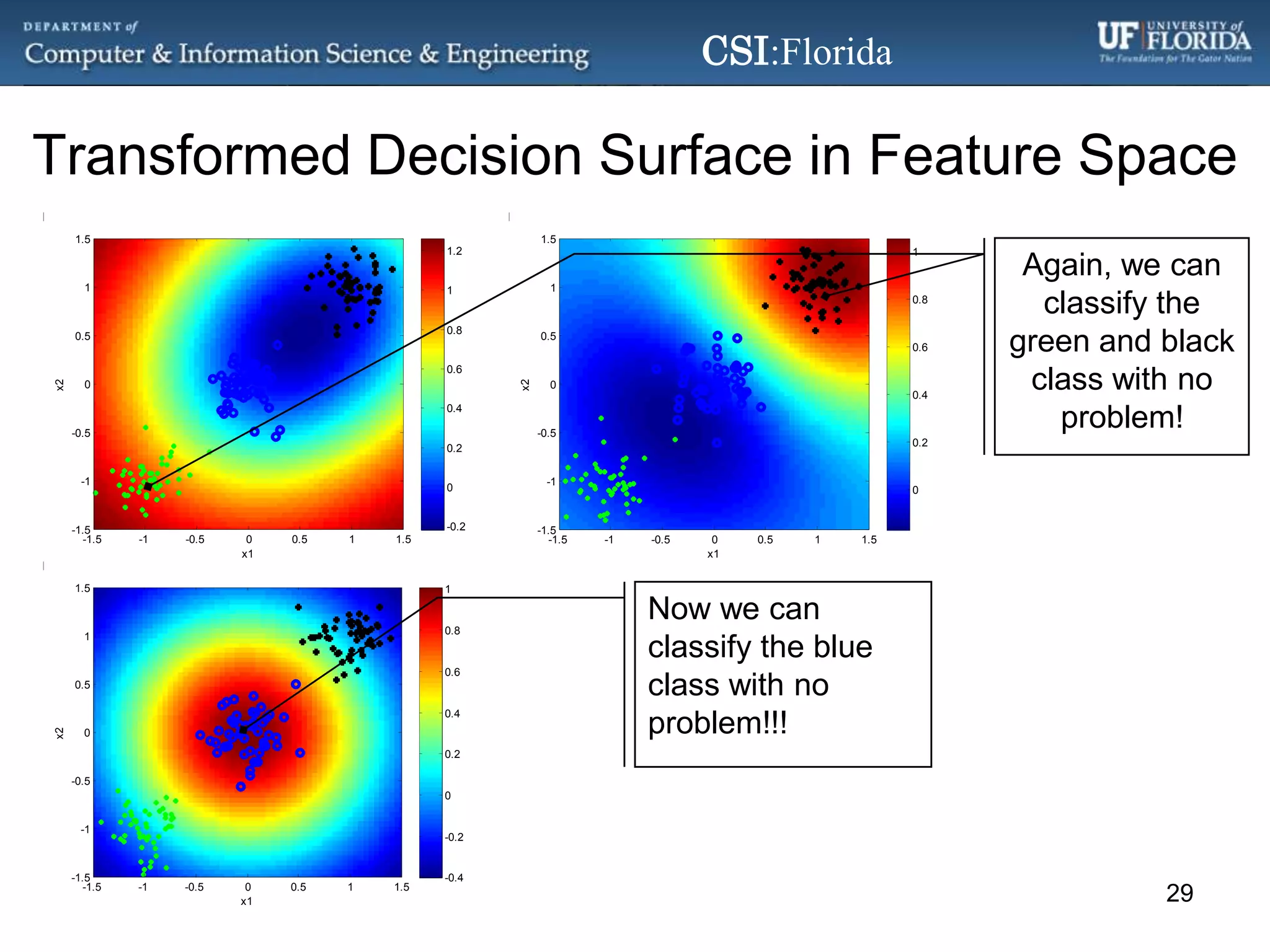
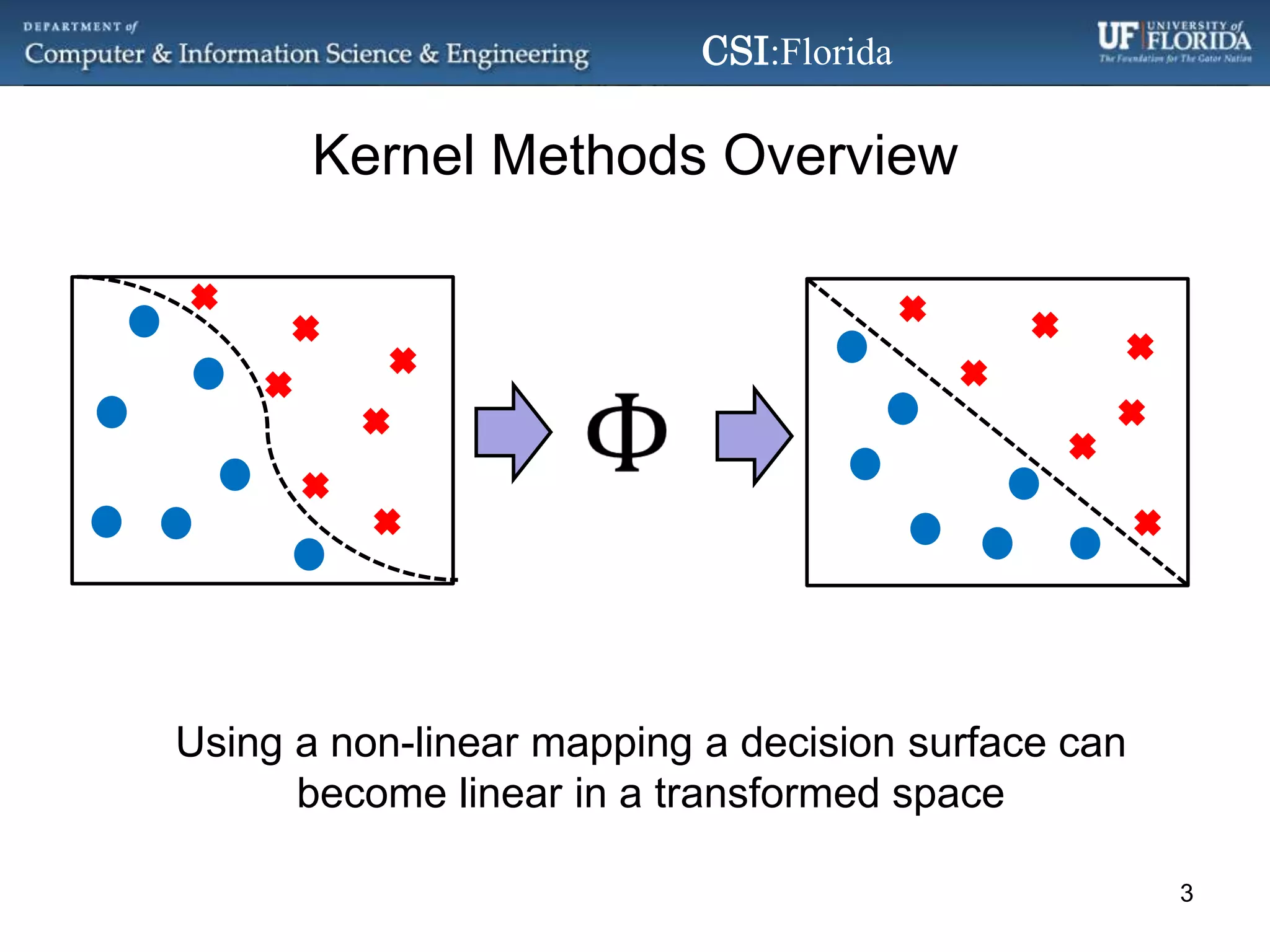
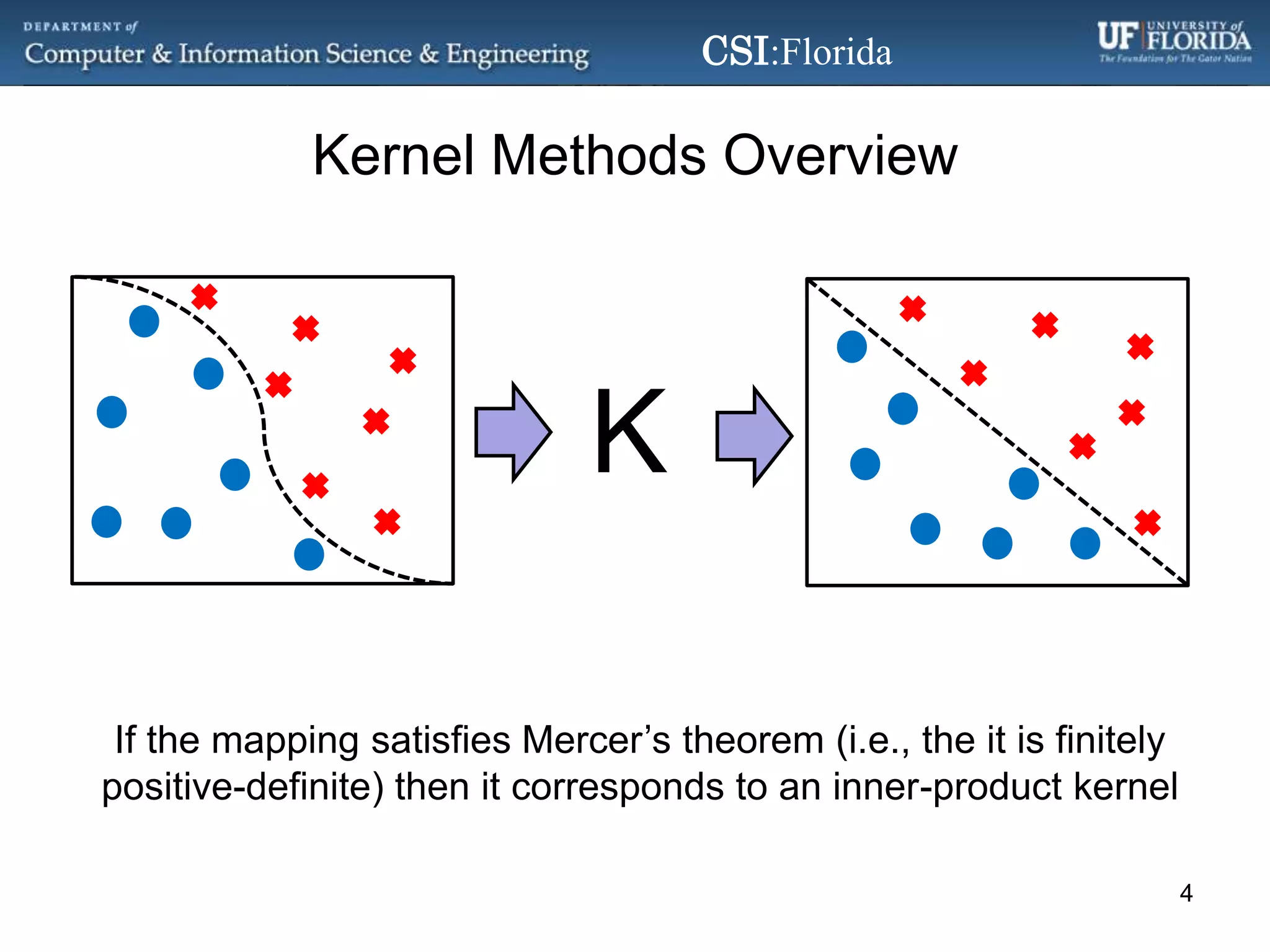
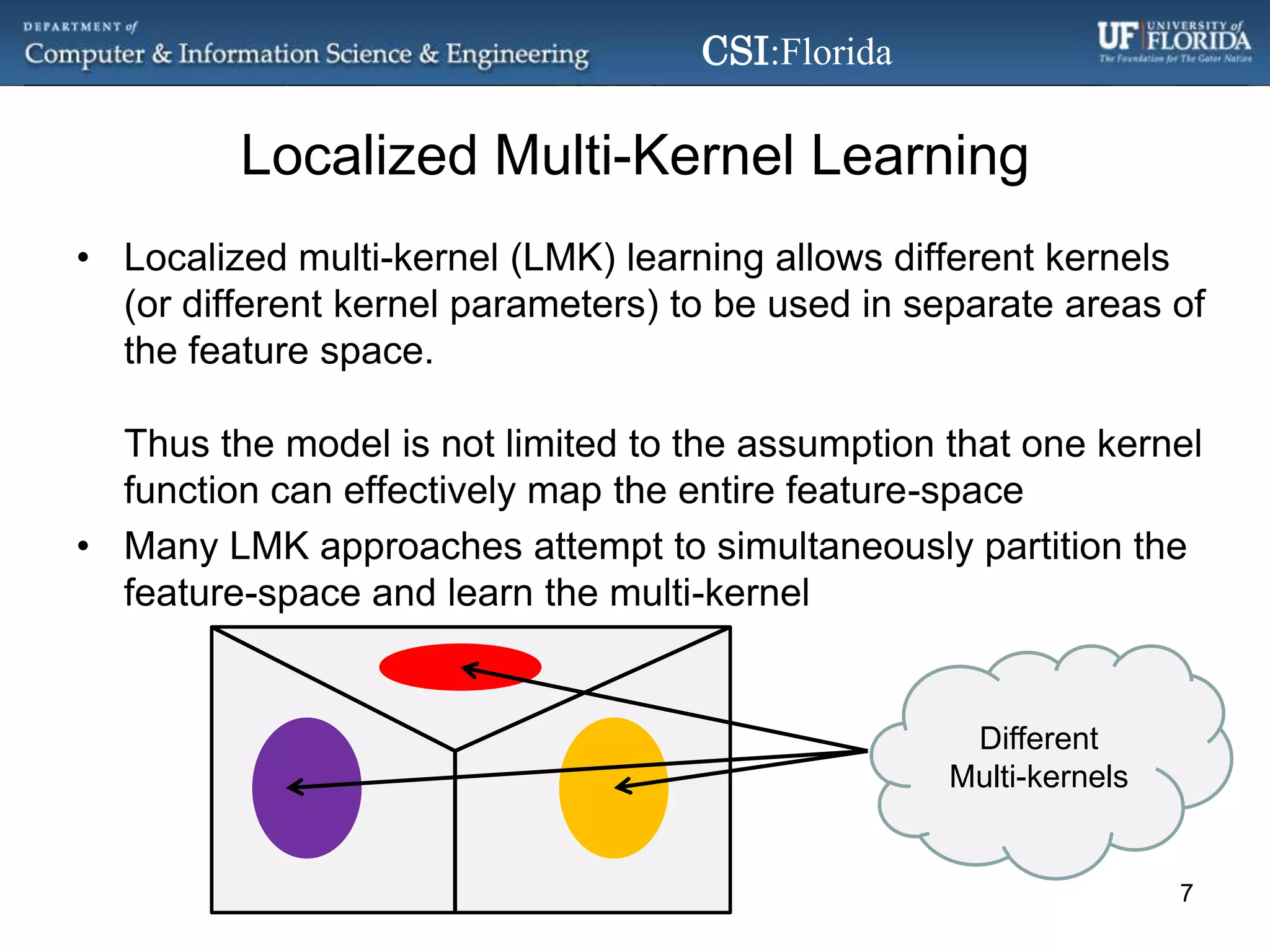
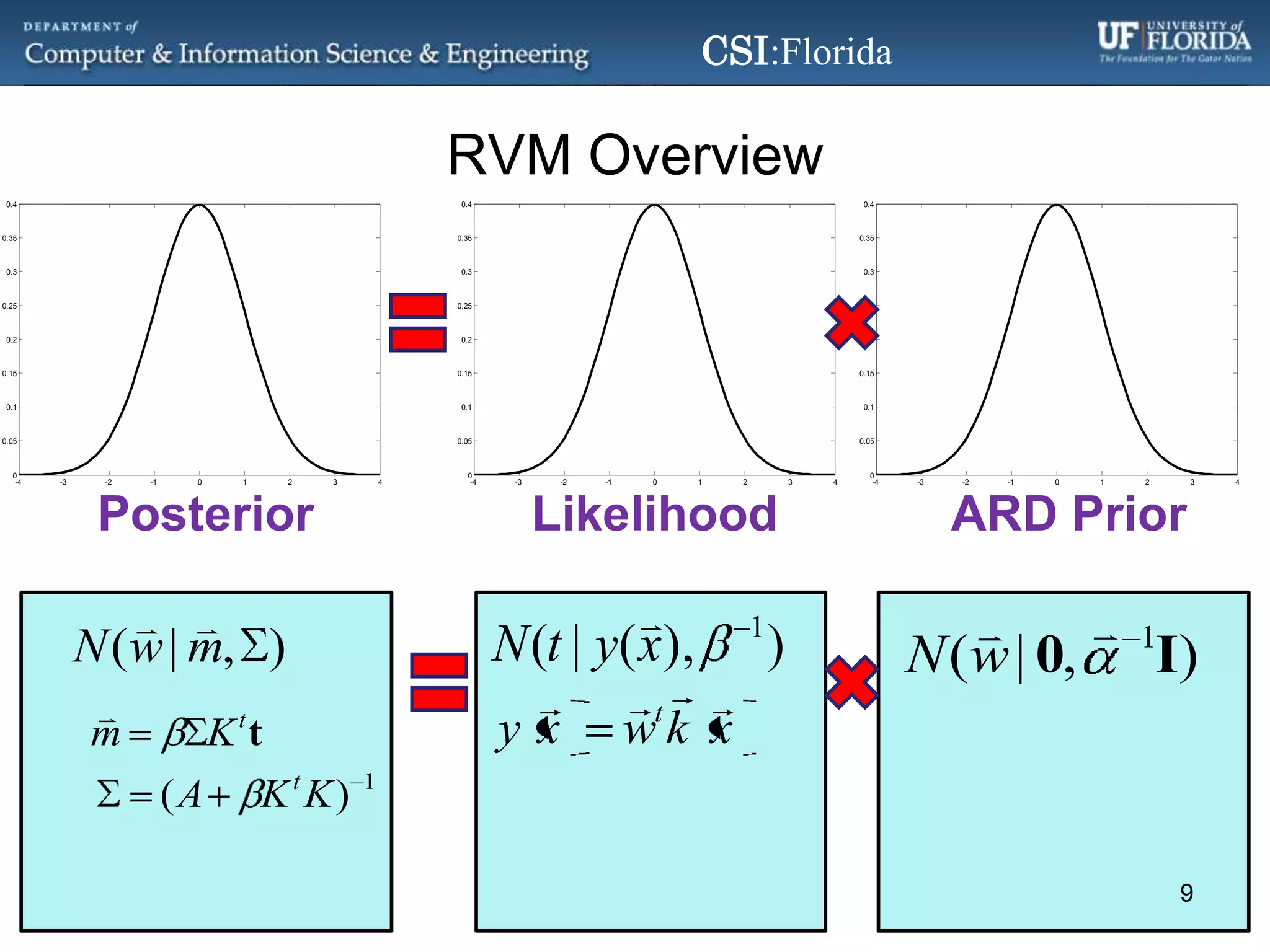
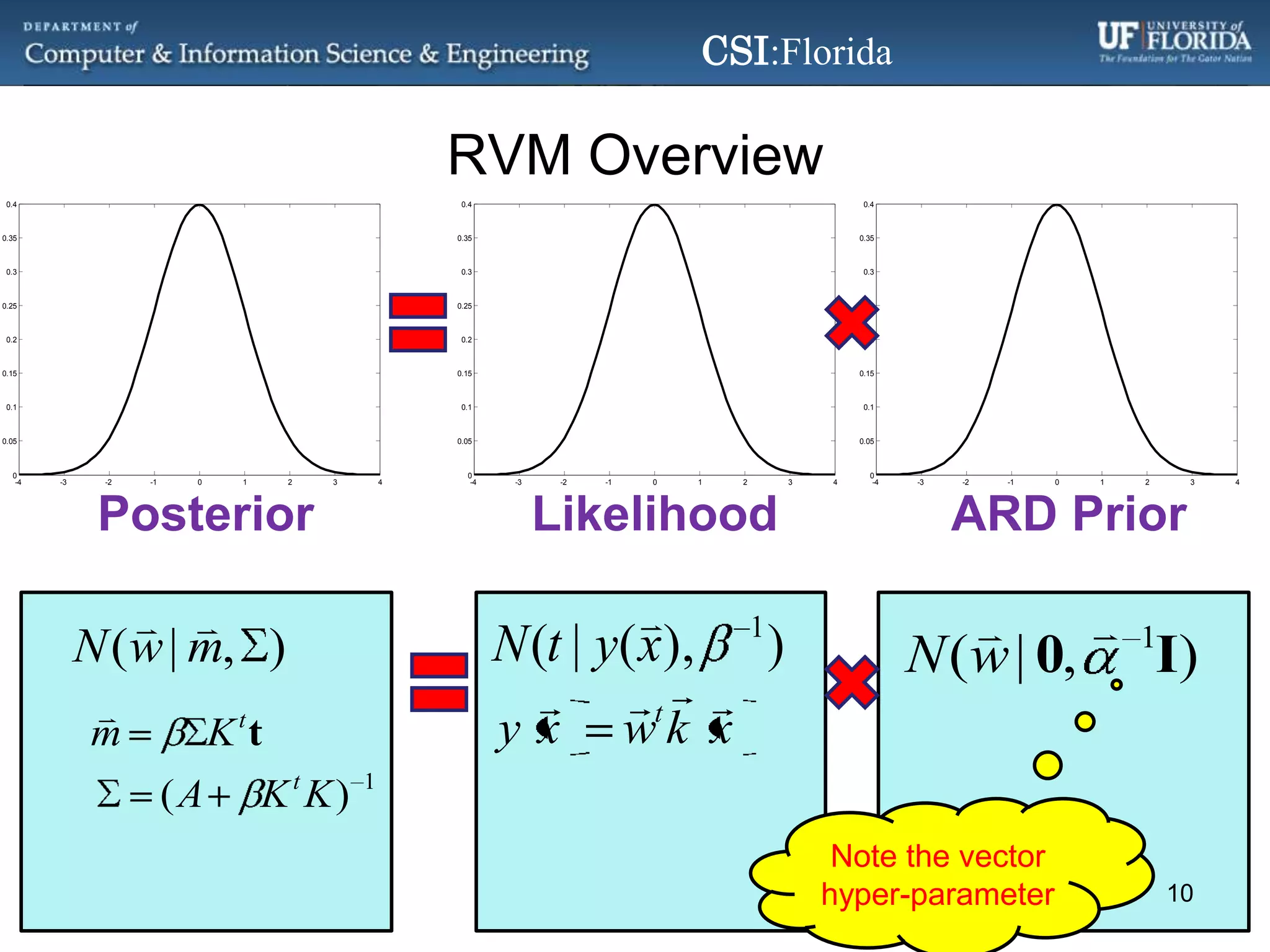
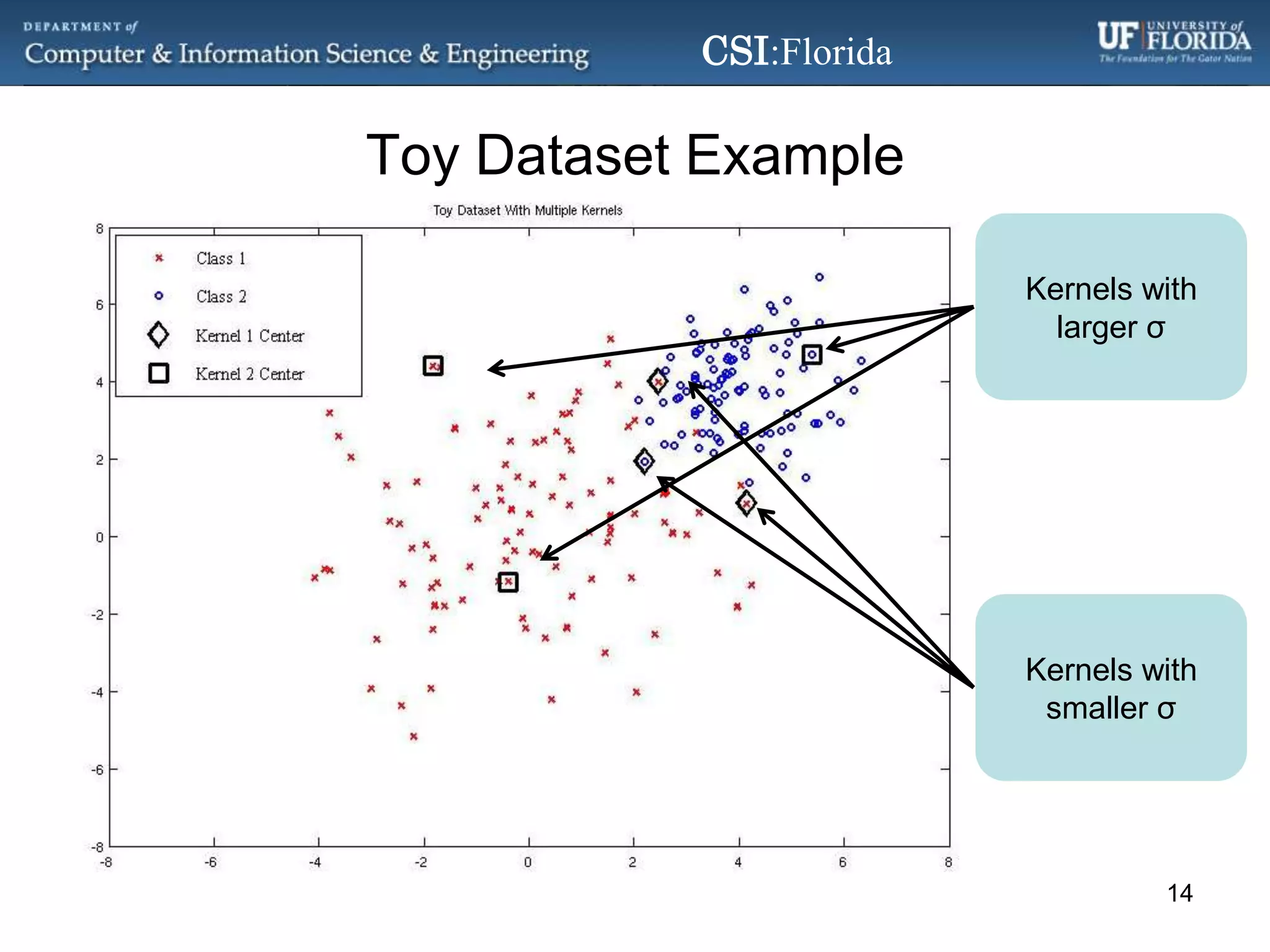
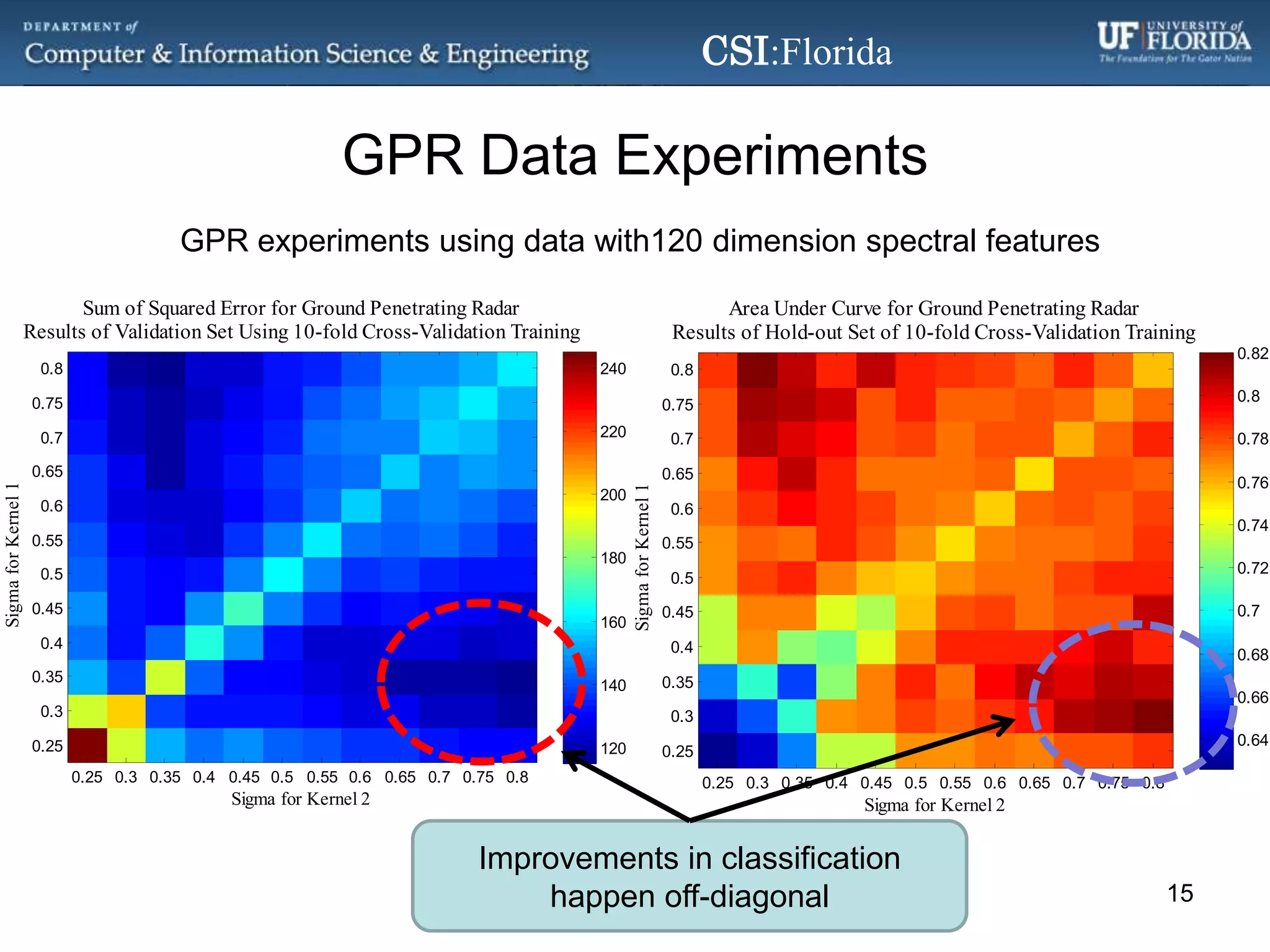
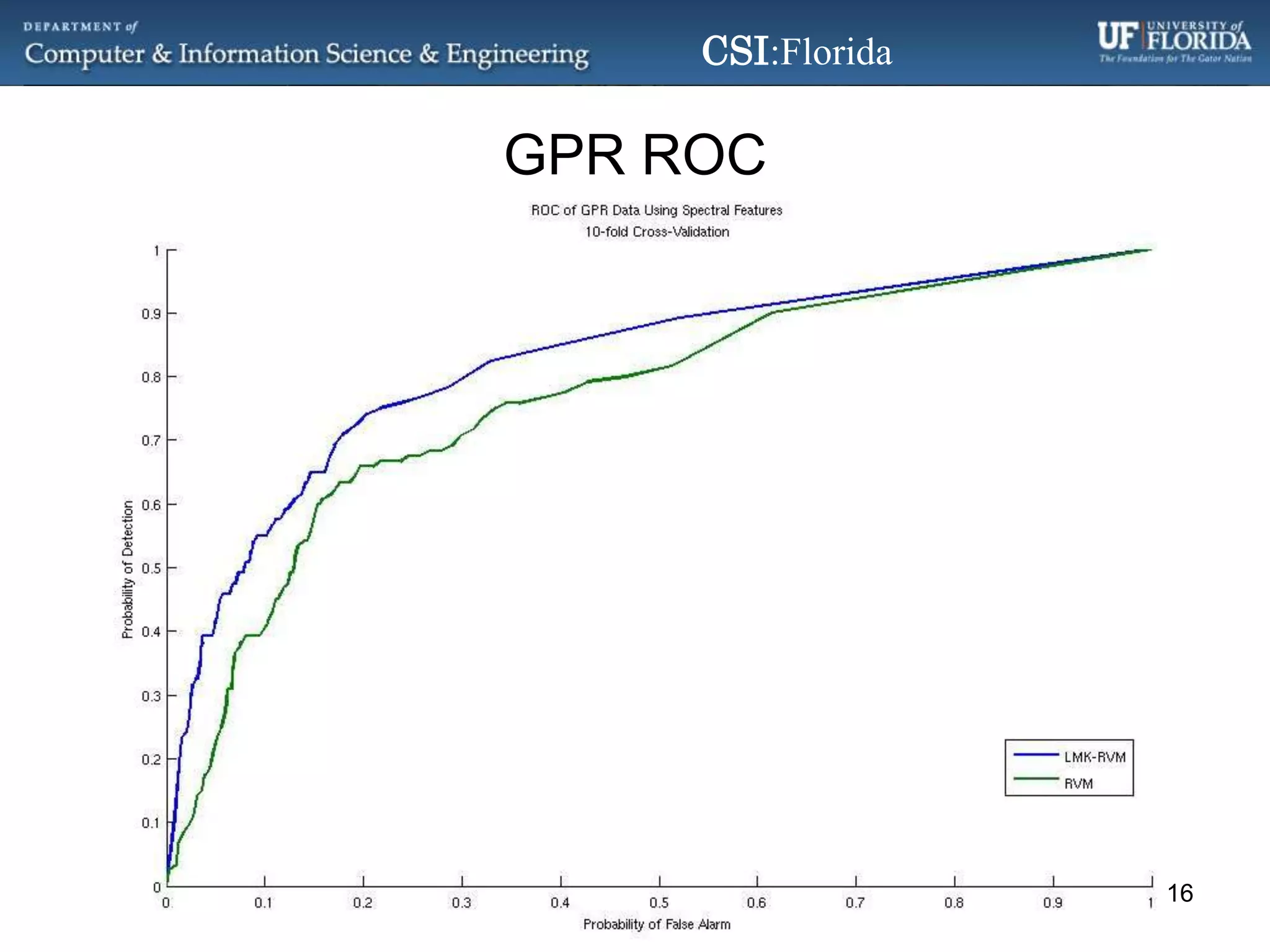
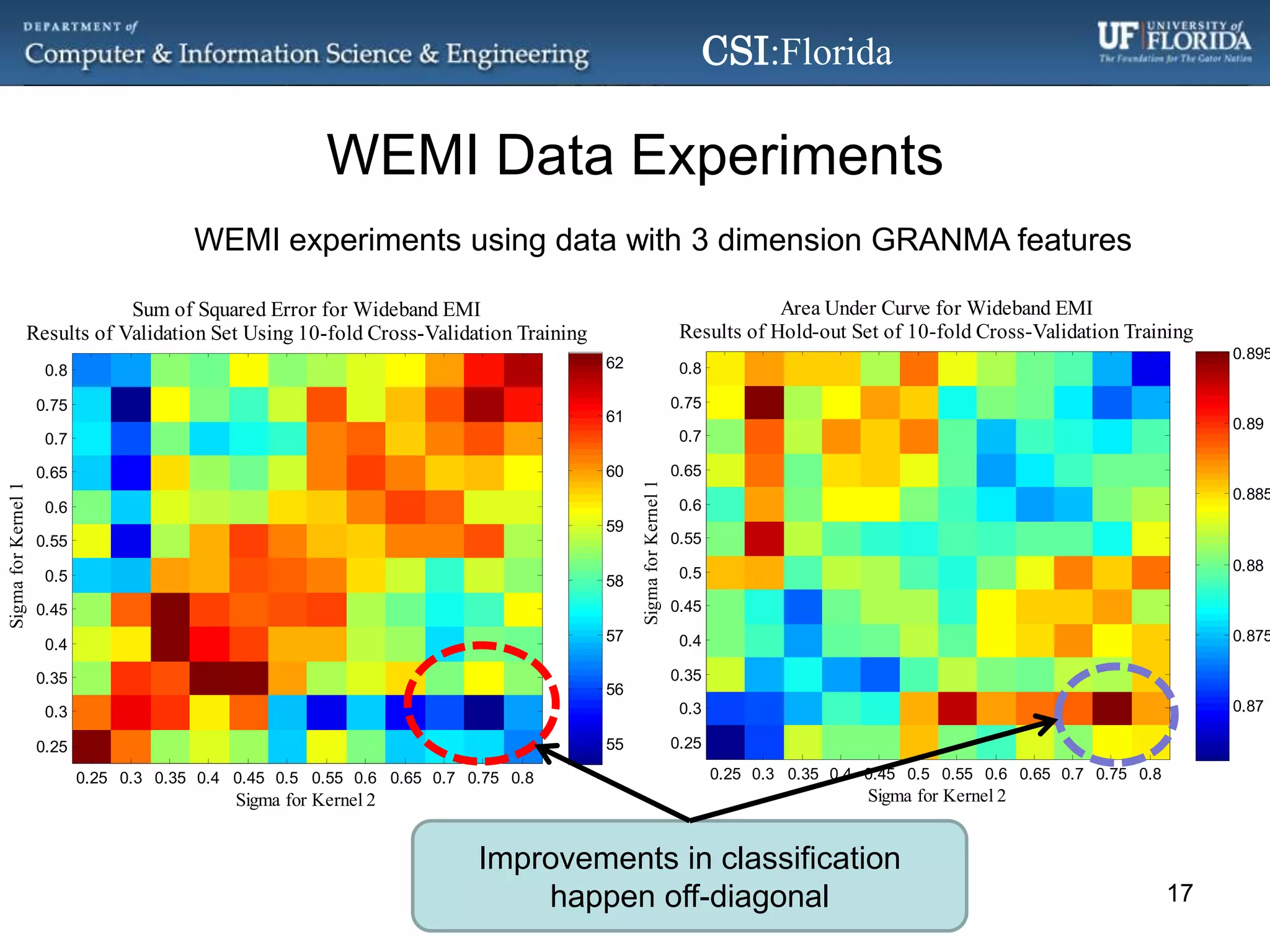
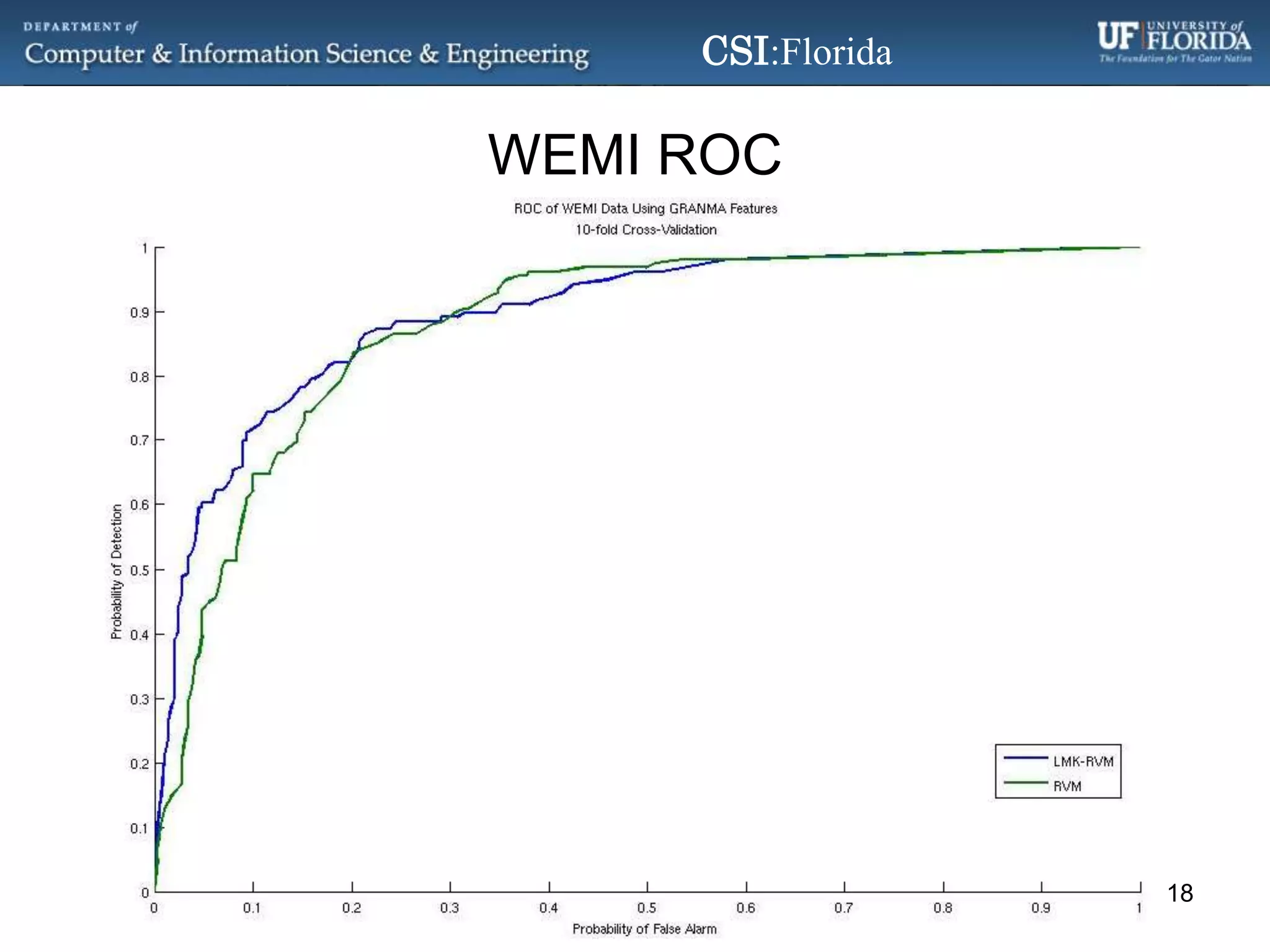
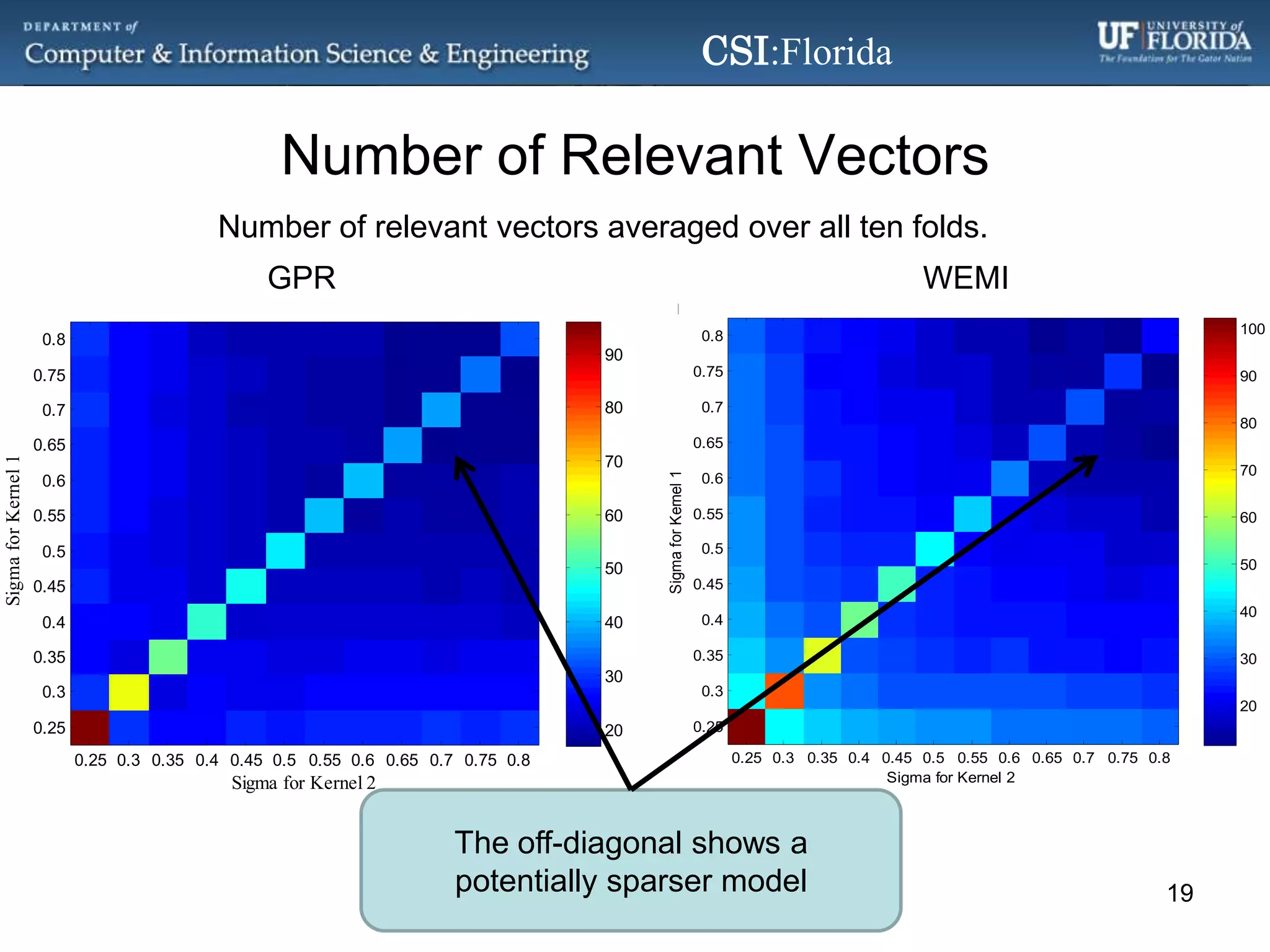
The document discusses a Bayesian approach called localized multi-kernel relevance vector machine (LMK-RVM) that uses multiple kernel functions to perform classification. LMK-RVM allows different kernel functions or parameters to be used in different areas of feature space, providing more flexibility than single-kernel models. It combines multi-kernel learning with the sparsity of the relevance vector machine (RVM) model. The document outlines LMK-RVM and provides examples showing it can improve classification accuracy and potentially provide sparser models compared to single-kernel approaches.

1. A Bayesian Approach to Localized Multi-Kernel Learning Using the Relevance Vector MachineR. Close, J. Wilson, P. Gader

2. OutlineBenefits of kernel methodsMulti-kernels and localized multi-kernelsRelevance Vector Machines (RVM)Localized multi-kernel RVM (LMK-RVM)Application of LMK-RVM to landmine detectionConclusions2

3. Kernel Methods OverviewΦ Using a non-linear mapping a decision surface can become linear in a transformed space3

4. Kernel Methods OverviewKIf the mapping satisfies Mercer’s theorem (i.e., the it is finitely positive-definite) then it corresponds to an inner-product kernel4

5. Kernel MethodsFeature transformations increase dimensionality to create a linear separation between classesUtilizing the kernel trick, kernel methods construct these feature transformations in an infinite dimensional space that can be finitely characterizedThe accuracy and robustness of the model becomes directly dependent on the kernel’s ability to represent the correlation between data pointsA side benefit is an increased understanding of the latent relationships between data points once the kernel parameters are learned5

6. Multi-Kernel LearningWhen using kernel methods, a specificform of kernel function is chosen (e.g. a radial basis function).Multi-kernel learning uses a linear combination of kernel functionsThe weights may be constrained if desiredAs the model is trained, the weights yielding the best input-space to kernel-space mapping are learned.Any kernel function whose weight approaches 0 is pruned out of the multi-kernel function.6

7. Localized Multi-Kernel LearningLocalized multi-kernel (LMK) learning allows different kernels (or different kernel parameters) to be used in separate areas of the feature space.Thus the model is not limited to the assumption that one kernel function can effectively map the entire feature-spaceMany LMK approaches attempt to simultaneously partition the feature-space and learn the multi-kernelDifferent Multi-kernels7

8. LMK-RVMA localized multi-kernel relevance vector machine (LMK-RVM) uses the ARD (automatic relevance determination) prior of the RVM to select the kernels to use over a given feature-space.This allows greater flexibility in the localization of the kernels and increased sparsity8

9. RVM OverviewLikelihoodPosteriorARD Prior9

10. RVM OverviewLikelihoodPosteriorARD PriorNote the vector hyper-parameter10

11. Automatic Relevance DeterminationValues for and are determined by integrating over the weights, and maximizing the resulting marginal distribution.Those training samples that do not help predict the output of other training samples have αvalues that tend toward infinity. Their associated w priors become δ functions with mean 0, that is, their weight in predicting outcomes at other points should be exactly 0. Thus, these training vectors can be removed.We can use the remaining, relevant, vectors to estimate the outputs associated with new data.The design matrix K=Φis now NxM, where M<<N.11

12. RVM for ClassificationStart with a two-class problemt  {0,1}() is logistic sigmoidSame as RVM for regression except must use IRLS to calculate the mode of the posterior distribution12

13. LMK-RVMUsing the multi-kernel with the RVM model, we start with:where wn is the weight on themulti-kernel associated with vector n and wi is the weight on the ith component of each multi-kernel.Unlike some kernel methods (e.g. SVM) the RVM is not constrained to use a positive-definite kernel matrix, thus, there is norequirement that the weights be factorized aswnwi. So, in this settingWe show a sample application of LMK-RVM using two radial basis kernels at each training point with different spreads.13

14. Toy Dataset ExampleKernels with larger σKernels with smaller σ14

15. GPR Data ExperimentsGPR experiments using data with120 dimension spectral featuresImprovements in classification happen off-diagonal15

16. GPR ROC16

17. WEMI Data ExperimentsWEMI experiments using data with 3 dimension GRANMA featuresImprovements in classification happen off-diagonal17

18. WEMI ROC18

19. Number of Relevant VectorsNumber of relevant vectors averaged over all ten folds.WEMIGPRThe off-diagonal shows a potentially sparser model19

20. ConclusionsThe experiment using GPR data features showed that LMK-RVM can provide definite improvement in SSE, AUC, and the ROCThe experiment using the lower-dimensional WEMI data GRANMA features showed that using the same LMK-RVM method provided some improvement in SSE and AUC and an inconclusive ROCBoth set of experiments show the potential for sparser models when choosing when using the LMK-RVMQuestion: is there an effective way to learn values for spreads in our simple class of localized multi-kernels?20

21. References[1] F. R. Bach, et al., "Multiple Kernel Learning, Conic Duality, and the SMO Algorithm," in International Conference on Machine Learning, Banff, Canada, 2004.[2] T. Damoulas, et al., "Inferring Sparse Kernel Combinations and Relevance Vectors: An Application to Subcellular Localization of Proteins," in Machine Learning and Applications, 2008. ICMLA '08. Seventh International Conference on, 2008, pp. 577-582.[3] G. Camps-Valls, et al., "Nonlinear System Identification With Composite Relevance Vector Machines," Signal Processing Letters, IEEE, vol. 14, pp. 279-282, 2007.[4] B. Wu, et al., "A Genetic Multiple Kernel Relevance Vector Regression Approach," in Education Technology and Computer Science (ETCS), 2010 Second International Workshop on, 2010, pp. 52-55.[5] R. A. Jacobs, et al., "Adaptive Mixtures of Local Experts," Neural Computation, vol. 3, pp. 79-87, 1991.[6] C. E. Rasmussen and Z. Ghahramani, "Infinite Mixtures of Gaussian Process Experts," in Advances in Neural Information Processing Systems, 2002.21

22. References[7] L. Yen-Yu, et al., "Local Ensemble Kernel Learning for Object Category Recognition," in Computer Vision and Pattern Recognition, 2007. CVPR '07. IEEE Conference on, 2007, pp. 1-8.[8] M. Gonen and E. Alpaydin, "Localized Multiple Kernel Learning," in 25th International Conference on Machine Learning, Helsinki, Finland, 2008.[9] M. Gonen and E. Alpaydin, "Localized Multiple Kernel Regression," in Pattern Recognition (ICPR), 2010 20th International Conference on, 2010, pp. 1425-1428.[10] M. E. Tipping, "The Relevance Vector Machine," Advances in Neural Information Processing Systems, vol. 12, pp. 652-658, 2000.[11] C. M. Bishop, "Relevance Vector Machines (Analysis of Sparsity)," in Pattern Recognition and Machine Learning, ed: Springer, 2007, pp. 349-353.[12] D. Tzikas, A. Likas, and N. Galatsanos. “Large Scale Multikernel Relevance Vector Machine for Object Detection,” International Journal on Artificial Intelligence Tools, 16(6):967-979, December 2007.[13] D. Tzikas, A. Likas, and N. Galatsanos, "Large Scale Multikernel RVM for Object Detection," presented at the Hellenic Conference on Artificial Intelligence, Heraclion, Crete, Greece, 2006.22

23. Backup SlidesExpanded Kernels Discussion23

24. Kernel Methods Example: The Masked Class ProblemIn both these problems linear classification methods have difficulty discriminating the blue class from the others!What is the actual problem here?No one line can separate the blue class from the other datapoints! Similar to the “single-layer” perceptron problem (The XOR problem)!24

25. Decision Surface in Feature SpaceCan classify the green and black class with no problem!Problems when we try to classify the blue class!!!!25

26. Revisit Masked Class ProblemAre linear methods completely useless on this data?-No, we can perform a non-linear transformation on the data via fixed basis functions!-Many times when we perform this transformation features that where not linearly separable in the original feature space become linearly separable in the transformed feature space.26

27. Basis Functions Models can be extended by using fixed basis functions which allows for linear combinations of nonlinear functions of the input variablesGaussian (or RBF) basis function:Basis vector: Dummy basis function used for bias parameter: Basis function center ( ) governs location in input spaceScale parameter () determines spatial scale27

28. Features in Transformed Space are Linearly SeparableTransformed datapoints are plotted in the new feature space28

29. Transformed Decision Surface in Feature SpaceAgain, we can classify the green and black class with no problem!Now we can classify the blue class with no problem!!!29

30. Common KernelsSquared Exponential: Gaussian Process Kernel:Automatic Relevance Determination (ARD) kernelOther kernels:Neural NetworkMatern-exponential, etc.30