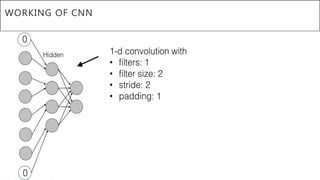
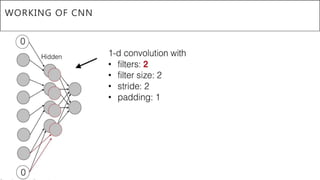
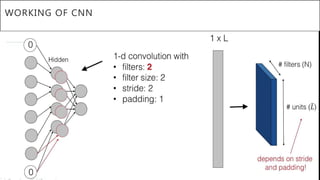
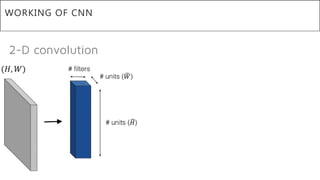
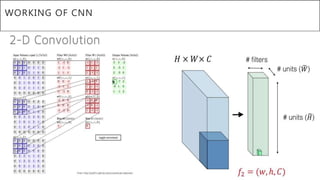
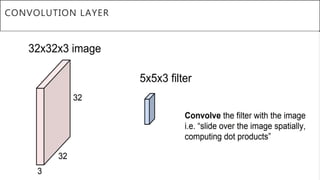
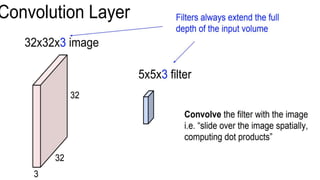
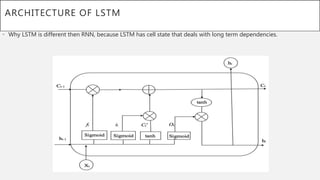
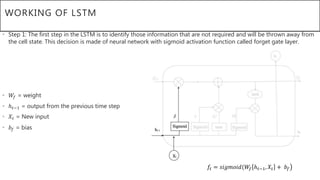
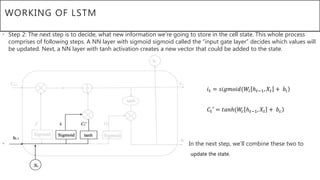
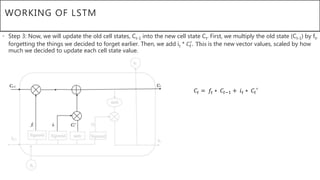
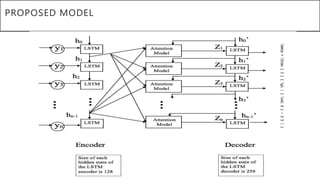
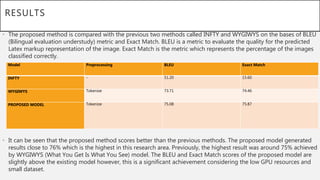
This document presents a thesis on using sequence-to-sequence learning with deep learning techniques for optical character recognition. The author aims to convert images of mathematical equations into LaTeX representations. Convolutional neural networks, recurrent neural networks, long short-term memory networks, and attention models are discussed as approaches. Details are provided on the architecture and workings of CNNs, RNNs, and LSTMs. The thesis will propose a model and discuss results and future work.

1. SEQUENCE-TO-SEQUENCE LEARNING USING
DEEP LEARNING FOR OPTICAL CHARACTER
RECOGNITION
Advisor
Dr. Devinder Kaur
Presented
By
Vishal Vijay Shankar Mishra

2. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

3. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

4. PROBLEM STATEMENT
•In this thesis, I have implemented a sequence-to-
sequence analysis using Deep Learning for Optical
Character Recognition.
•I have used the images of the mathematical equations to
convert it into LATEX representation.

5. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

6. APPROACH (DEEP LEARNING TECHNIQUES)
• To accomplish this research work, I have used the following deep
learning techniques.
Convolutional Neural Network (CNN)
Recurrent Neural Network (RNN)
Long Term-Short Memory (LSTM)
Attention model.
• In the subsequent slides, I’ll try to give the gist of the techniques.

7. WHAT IS DEEP NEURAL NETWORK?
• Deep Neural Networks are those networks that have more than 2 layer to perform the task.

8. WHY DO WE NEED DEEP NEURAL NETWORK?
• Neural nets tend to be computationally expensive for data with simple
patterns; in such cases you should use a model like Logistic Regression or
an SVM.
• As the pattern complexity increases, neural nets start to outperform other
machine learning methods.
• At the highest levels of pattern complexity –for example high-resolution
images
• – neural nets with a small number of layers will require a number of nodes
that grows exponentially with the number of unique patterns. Even then,
the net would likely take excessive time to train, or simply would fail to

9. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

10. WHY CONVOLUTIONAL NEURAL NETWORK?

11. WHY CONVOLUTIONAL NEURAL NETWORK?

12. WHY CONVOLUTIONAL NEURAL NETWORK?

13. WHY CONVOLUTIONAL NEURAL NETWORK?

14. WHY CONVOLUTIONAL NEURAL NETWORK?

15. INTRODUCTION TO CNN
• Architecture of CNN

16. WORKING OF CNN

17. WORKING OF CNN

18. WORKING OF CNN

19. WORKING OF CNN

20. WORKING OF CNN

21. WORKING OF CNN

22. WORKING OF CNN

23. WORKING OF CNN

24. WORKING OF CNN

25. WORKING OF CNN

26. WORKING OF CNN

27. WORKING OF CNN

28. WORKING OF CNN

29. WORKING OF CNN

30. WORKING OF CNN

31. WORKING OF CNN

32. WORKING OF CNN

33. WORKING OF CNN

34. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

35. LAYERS IN CNN

36. CONVOLUTION LAYER

37. CONVOLUTION LAYER

64. NON-LINEAR ACTIVATION LAYER (RELU)
• ReLU is a non-linear activation function, which is used to apply elementwise non-linearity.
• ReLU layer applies an activation function to each element, such as the max(0, x) thresholding to zero.

68. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

69. HYPER-PARAMETERS
• Convolution
• Filter Size
• Number of Filters
• Padding
• Stride
• Pooling
• Filter Size
• Stride
• Fully Connected
• Number of neurons

70. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

71. INTRODUCTION TO RNN
• RNNs are a type of artificial neural network designed to recognize the patterns in sequences of data. It is used to
process the data sequentially.
• Why can’t we accomplish this task with Feed forward network?
• The drawback of feed forward network is that, it doesn't remember the inputs over the period of time.
• To process the data sequentially we need a network that behave recurrently.
• Architecture of RNN
RNN have
loop

72. • RNNs are not all that different than Neural Network. RNN can be thought of as multiple copies of the same network,
each passing a message to a successor. An unrolled RNN is shown below.
• In fast last few years, there have been incredible success applying RNNs to a variety of problems: speech recognition,
language modeling, translation, image captioning…. The list goes on.
An Unrolled RNN

73. DRAWBACK OF AN RNN
• RNN has a problem of long term dependency. It doesn’t remember the inputs after certain time steps.
• This problem occurs due to gradient exploding or gradient vanishing while performing backpropagation.
• I’ll try to example this problem with an example.
• Let’s consider a language model trying to predict the next word based on the previous ones.
• For example “the clouds are in the sky ”. So in order to predict the sky we don’t need any further context.
In such cases, where the gap between the relevant information and the place that it’s needed is small, RNNs can
learn to use the past information

74. • But there are also cases where we need to know more context of the input.
• For example “I grew up in France ……………………………. I speak fluent French” .
• Unfortunately, as that gap grows, RNNs become unable to learn to connect the information.
• This happens due to vanishing gradient and exploding gradient problem.

75. VANISHING GRADIENT

76. EXPLODING GRADIENT

77. HOW TO OVERCOME THESE CHALLENGES?
• For Vanishing gradient we can use,
ReLu activation function: We can use activation functions like
ReLU, which gives output one while calculating gradient.
LSTM, GRUs : Different network architectures that has been
specially designed can be used to combat this problem.
• For Exploding gradient we can use,
Clip gradients at threshold: clip the gradient when it goes
higher than a threshold.

78. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results and Future work
• Conclusion

79. LONG SHORT-TERM MEMORY (LSTM)
• Long Short Term Memory network – usually just called “LSTM” – are a special kind of RNN
• They are capable of learning long-term dependencies.

80. ARCHITECTURE OF LSTM
• Why LSTM is different then RNN, because LSTM has cell state that deals with long term dependencies.

81. WORKING OF LSTM
• Step 1: The first step in the LSTM is to identify those information that are not required and will be thrown away from
the cell state. This decision is made of neural network with sigmoid activation function called forget gate layer.
• 𝑊𝑓 = weight
• ℎ 𝑡−1 = output from the previous time step
• 𝑋𝑡 = New input
• 𝑏𝑓 = bias
𝑓𝑡 = 𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝑊𝑓 ℎ 𝑡−1, 𝑋𝑡 + 𝑏𝑓

82. WORKING OF LSTM
• Step 2: The next step is to decide, what new information we’re going to store in the cell state. This whole process
comprises of following steps. A NN layer with sigmoid sigmoid called the “input gate layer” decides which values will
be updated. Next, a NN layer with tanh activation creates a new vector that could be added to the state.
• In the next step, we’ll combine these two to
• V update the state.
𝑖 𝑡 = 𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝑊𝑖 ℎ 𝑡−1, 𝑋𝑡 + 𝑏𝑖
𝐶𝑡′ = 𝑡𝑎𝑛ℎ(𝑊𝑐 ℎ 𝑡−1, 𝑋𝑡 + 𝑏 𝑐

83. WORKING OF LSTM
• Step 3: Now, we will update the old cell states, Ct-1 into the new cell state Ct. First, we multiply the old state (Ct-1) by ft,
forgetting the things we decided to forget earlier. Then, we add it * 𝐶𝑡
′
. This is the new vector values, scaled by how
much we decided to update each cell state value.
𝐶𝑡 = 𝑓𝑡 ∗ 𝐶𝑡−1 + 𝑖 𝑡 ∗ 𝐶𝑡′

84. WORKING OF LSTM
• Step 4: We will run a sigmoid layer which decides what parts of the cell state we’re going to output. Then, we put the
cell state through tanh (push the values to be between -1 and 1) and multiply it by the output of the sigmoid gate,
so that we only output the parts we decided to.
𝑂𝑡 = 𝑠𝑖𝑔𝑚𝑜𝑖𝑑(𝑊𝑜 ℎ 𝑡−1, 𝑋𝑡 + 𝑏 𝑜
ℎ 𝑡 = 𝑂𝑡 ∗ tan h( 𝐶𝑡 s

85. PROPOSED LSTM VARIANT WITH PEEPHOLE CONNECTION
• The easiest but very powerful solution to the conventional LSTM unit is to introduce a weighted “peephole”
connections from the cell state unit (Ct-1) to all the gates in the same memory unit. The peephole connections allow
every gate to assess the current cell state even though the output gate is closed.

86. STOCHASTIC “HARD” ATTENTION MODEL
• With an attention mechanism, the image is first
divided into n, parts, and we compute with a
CNN representations of each part y1,y2………yn.
When LSTM is generating a new word, the
attention mechanism is focusing on the
relevant part of the image, so the decoder only
uses specific parts of the image.
• In stochastic process like Hard attention
mechanism, rather than using all the hidden
states yt as an input for the decoding, the
process finds the probabilities of a hidden state
with respect to location variable 𝑠𝑡. The
gradients are obtained by reinforcement
learning.

87. AGENDA
• Problem Statement
 Converting Mathematical Equations into Latex
representation.
• Approach (Deep Learning Techniques)
 Convolutional Neural Network (CNN)
 Recurrent Neural Network (RNN)
 Long Term-Short Memory (LTSM)
 Attention Model
• Introduction to CNN
 Gist of Neural Network
 Architecture of CNN
• CNN layers
 Convolution Layer
 Non-Linear Activation Layer (ReLu)
 Pooling Layer
• Hyper-Parameters.
• Introduction to RNN
 Architecture of RNN
 Working of RNN
 RNN Example
• Drawback of RNN
• LSTM
 Architecture of LSTM
 Working of LSTM
 LSTM Example
• Proposed Model
• Results
• Conclusion and Future work

88. PROPOSED MODEL

89. PROPOSED MODEL

90. • Original Image
• Predicted Latex:
• Rendered Predicted Image:
Actual Test results on Test set:

91. RESULTS
• The proposed method is compared with the previous two methods called INFTY and WYGIWYS on the bases of BLEU
(Bilingual evaluation understudy) metric and Exact Match. BLEU is a metric to evaluate the quality for the predicted
Latex markup representation of the image. Exact Match is the metric which represents the percentage of the images
classified correctly.
• It can be seen that the proposed method scores better than the previous methods. The proposed model generated
results close to 76% which is the highest in this research area. Previously, the highest result was around 75% achieved
by WYGIWYS (What You Get Is What You See) model. The BLEU and Exact Match scores of the proposed model are
slightly above the existing model however, this is a significant achievement considering the low GPU resources and
small dataset.
Model Preprocessing BLEU Exact Match
INFTY - 51.20 15.60
WYGIWYS Tokenize 73.71 74.46
PROPOSED MODEL Tokenize 75.08 75.87

92. Actual Test results on Test set:

93. FUTURE WORK.
• For possible future work, this research can be scaled from printed
mathematical formulas images to the hand written mathematical
formulas images. To recognize the hand written mathematical
formulas, one can implement the bidirectional LSTM with CNN
• This model can be used to solve the mathematical question
based on formulas.
• An API (Application Program Interface) can be created to solve
the mathematical problems.

94. REFERENCES.
[1] R. 1. Anderson, Syntax-directed recognition of handprinted mathematics., CA: Symposium, 1967.
[2] K. Cho, A. Courville and Y. Bengio, "Describing Multimedia Content Using Attention-Based Encoder-Decoder Networks," in IEEE, CA, 2015.
[3] A. K. a. E. Learned-Miller, "Learning on the Fly: Font-Free Approaches to Difficult OCR Problems," MA, 2000.
[4] D. Lopresti, "Optical Character Recognition Errors and Their Effects on Natural Language Processing," International Journal on Document Analysis and Recognition, 19 12
[5] WILDML, "WILDML," [Online]. Available: http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/.
[6] S. a. S. J. Hochreiter, "Long Short-Term Memory. Neural Computation," 1997.
[7] S. Yan, "Understanding LSTM and its diagrams," Software engineer & wantrepreneur. Interested in computer graphics, bitcoin and deep learning., 13 03 2016. [Online]. [1]
https://medium.com/@shiyan/understanding-lstm-and-its-diagrams-37e2f46f1714.
[8] C. R. a. D. P. W. Ellis, "FEED-FORWARD NETWORKS WITH ATTENTION CAN SOLVE SOME LONG-TERM MEMORY PROBLEMS," ICLR, 2016.
[9] a. F.-F. L. Karpathy, Image captioning., 2015.
[10] F. A. Gers, N. N. Schraudolph and J. Schmidhuber, "Learning Precise Timing with LSTM Recurrent Networks," Journal of Machine Learning Reserach, 8 2002.

95. •Questions ???????????

96. •Thank You !!!!!!!!!