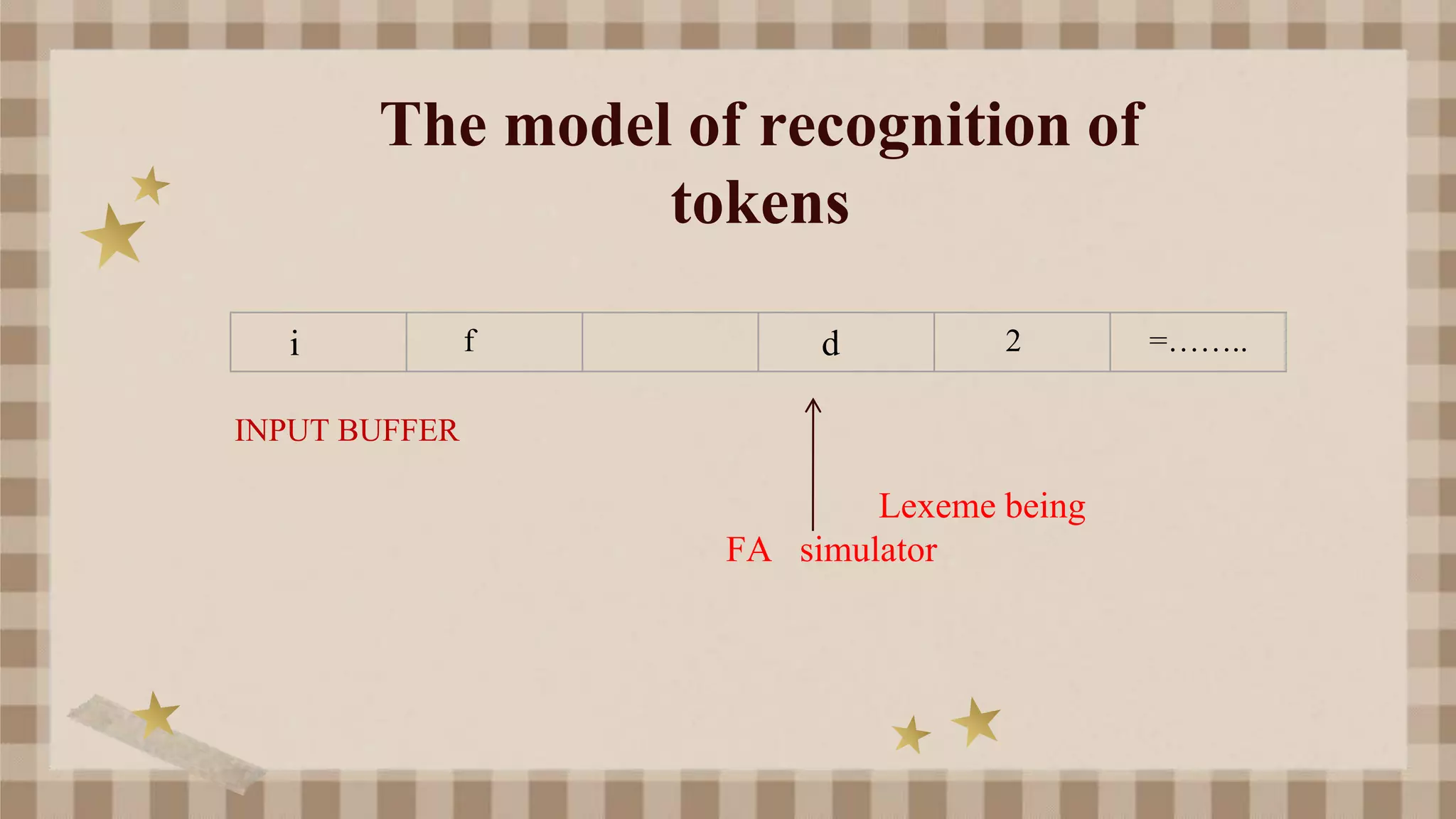
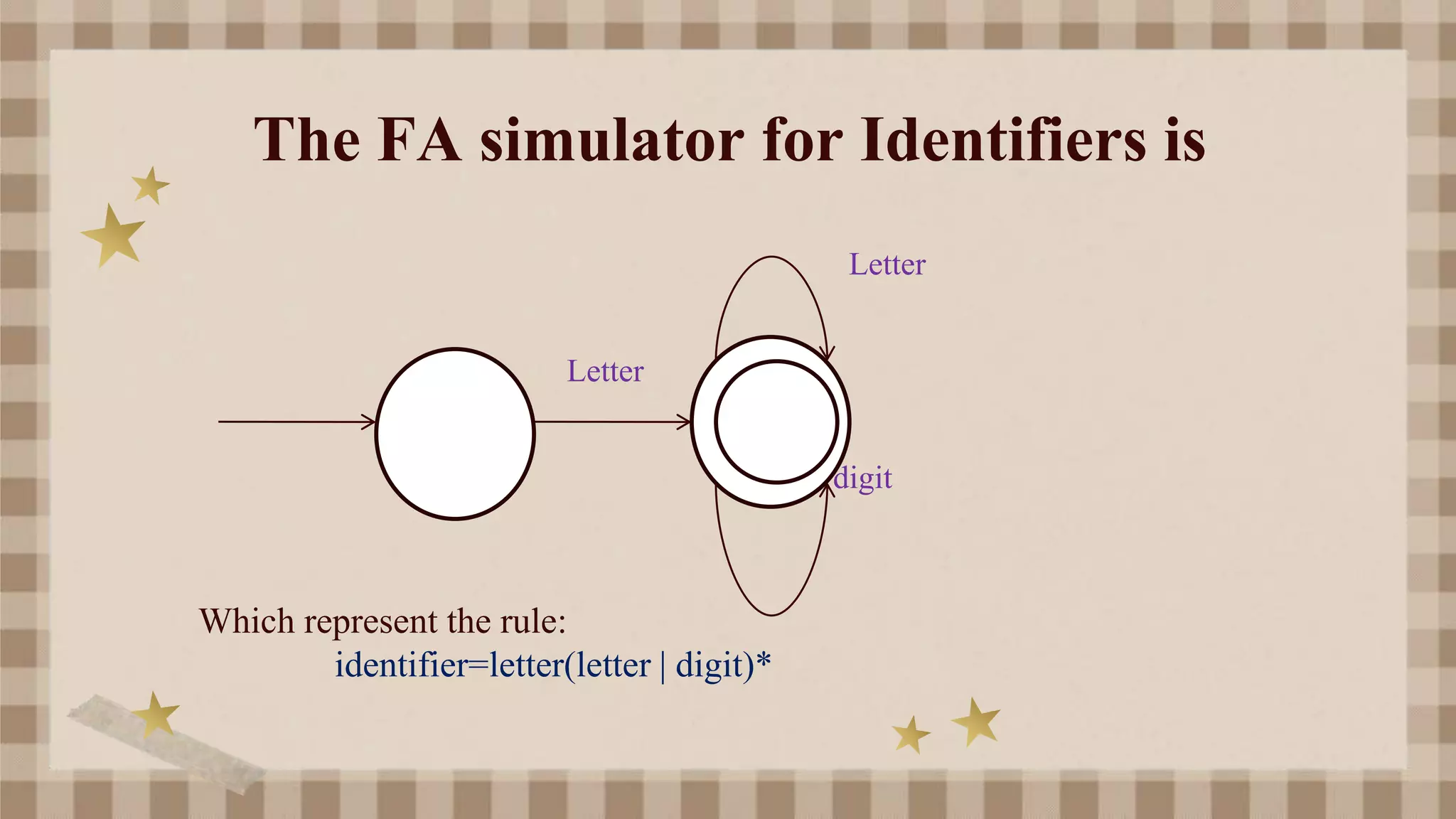
The document outlines a straightforward method for designing lexical analyzers, which involves creating token structure diagrams and converting them into token-finding programs. It discusses the use of regular expressions to specify tokens and the transition diagram for both deterministic and non-deterministic finite automata. Additionally, it covers the processes involved in lexical analysis, such as error message correlation and pattern matching techniques.

1. A SIMPLE APPROACH TO THE DESIGN OF
LEXICAL ANALYZERS
Myself Archana R
Assistant Professor In
Department Of Computer Science
SACWC.
I am here because I love to give presentations.

2. Simple Approach
Construct a diagram that illustrates the structure of the tokens of the
source language , and then to hand-translate the diagram
the diagram into a program for finding tokens.
Notes:
Efficient lexical analyzers can be produced in this manner.

3. Simple Approaches To Implement A
Lexical Analyzer
Pattern-directed programming approach
 Pattern Matching technique.
 Specify and design program that execute actions triggered by
patterns in strings.
 Introduce a pattern-action language called Lexical for specifying
lexical analyzers .
 Patterns are specified by regular expressions .
 A compiler for Lexical can generate an efficient finite
automation recognizer for the regular expressions.

4. First phase of a compiler
1. Main task
- To read the input characters.
- To produce a sequence of tokens used by the parser for
syntax analysis.
- As an assistant of parser.

5.  Lexical analyzer
 Parser
 Symbol table
 Source program
 token
 Get next token
Interaction of lexical analyzer with parser

6. Processes in lexical analyzers
 Scanning
*Pre-processing
-Strip out comments and white space
-Macro functions
 Correlating error messages from compiler with source
program
*A line number can be associated with an error
message.
 Lexical analysis

7. Regular Expression & Regular language
 Regular Expression
A notation that allows us to define a pattern in a high
level language.
 Regular language
Each regular expression r denotes language L(r) (the
set of sentences relating to the regular expression r) .
Notes:
Each word in a program can be expressed in a regular
expression.

8. Specification of Tokens
1) The rule of regular expression over alphabet ∑
* ε is a regular expression that denote {ε}
ε is regular expression .
{ε} is the related regular language.
2) If a is a symbol in ∑, then a is a regular expression that
denotes {a}
a is regular expression .
{a} is the related regular language.

9. 3) Suppose α and β are regular expressions, then α| β, α β, α * , β *
is also a regular expression.
Notes : Rules 1) and 2) form the basis of the definition; rule 3)
provides the inductive step.
4) Algebraic laws of regular expressions
1) α| β = β | α 2) α |(β |γ)=(α | β)| γ α(β γ) =(α β) γ
3)εα = αε= α 5)(α *)*= α *
6) α *= α ＋|ε α ＋ ＝ α α * = α * α
7) (α | β)*= (α * | β *)*= (α * β *)*

10. Notational Short-hands
a)One or more instances
( r ) digit+
b)Zero or one instance
r? is a shorthand for r| (E(+|-)?digits)?
c)Character classes
[a-z] denotes a|b|c|…|z
[A-Za-z] [A-Za-z0-9]

11. Implementing a Transition Diagram
 Each state gets a segment of code.
 If there are edges leaving a state, then its code reads a character and
selects an edge to follow, if possible.
 Use next char() to read next character from the input buffer.
A generalized transition diagram Finite Automation
 Deterministic or non-deterministic FA.
 Non-deterministic means that more than one transition out of a state
may be possible on the same input symbol.

12. The model of recognition of
tokens
INPUT BUFFER
Lexeme being
FA simulator
i f d 2 =……..

13. The FA simulator for Identifiers is
Letter
Letter
digit
Which represent the rule:
identifier=letter(letter | digit)*

14. Deterministic FA (DFA)
1) In a DFA, no state has an transition.
2)In a DFA, for each state s and input symbol a,
there is at most one edge labeled a leaving s.
3)To describe a FA , we use the transition graph or
transition table .
4)A DFA accepts an input string x if and only if
there is some path in the transition graph from start
state to some accepting state.

15. So ,the DFA is
M=({0,1,2,3,},{a,b,c}, move,0,{1,2,3})
move：move(0,a)=1
move(0,b)=1 move(0,c)=1
move(1,a)=1 move(1,b)=1
move(1,c)=1 move(2,a)=3
move(2,b)=2 move(2,c)=2
move(3,b)=3 move(3,c)=3 32

16. A generalized transition diagram
 Finite Automation
Deterministic or non-deterministic FA
Non-deterministic means that
more than one transition out of a state may be
possible on the same input symbol.

17. Non-deterministic FA (NFA)
1) In a NFA the same character can label two or more transitions out
of one state.
2) In a NFA is a legal input symbol.
3) A DFA is a special case of a NFA.
4)A NFA accepts an input string x if and only if there is some path in
the transition graph from start state to some accepting state. A
path can be represented by a sequence of state transitions called
moves.
5) It accepts the language defined by a NFA is the set of input strings.

18. Thank you