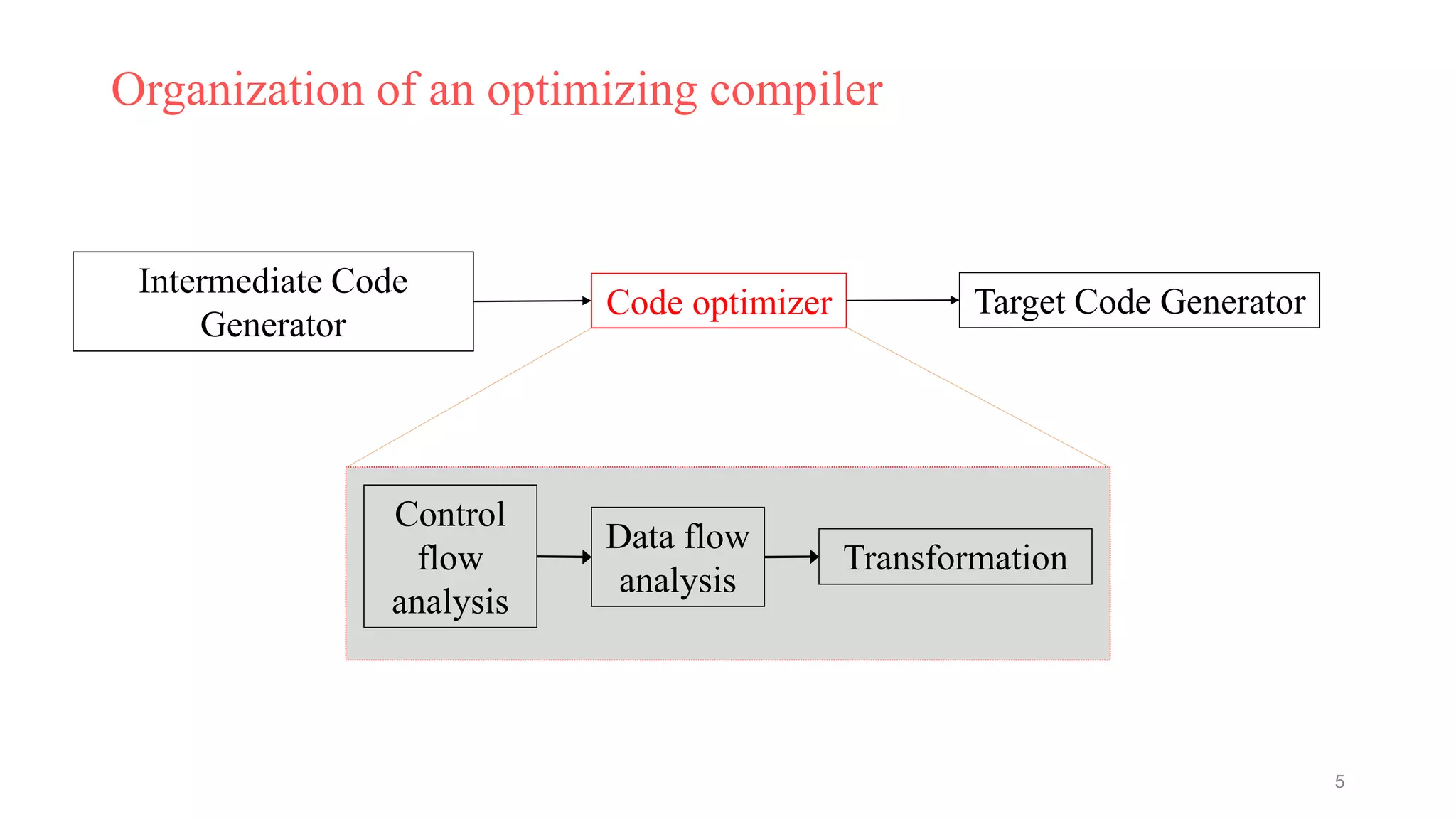
The document discusses code optimization techniques in compilers. It covers the following key points:
1. Code optimization aims to improve code performance by replacing high-level constructs with more efficient low-level code while preserving program semantics. It occurs at various compiler phases like source code, intermediate code, and target code.
2. Common optimization techniques include constant folding, propagation, algebraic simplification, strength reduction, copy propagation, and dead code elimination. Control and data flow analysis are required to perform many optimizations.
3. Optimizations can be local within basic blocks, global across blocks, or inter-procedural across procedures. Representations like flow graphs, basic blocks, and DAGs are used to apply optimizations at








![Basic Block Example
{
prod =0;
i =1;
do
{
prod =prod+ a[i] * b[i];
i =i+1;
}
while i < = 20
} 10
• Source code for dot product of two vectors a and
b of length 20 prod = 0
i = 1
L1: t1 = 4* i
t2 = a[t1] /*compute a[i] */
t3 = 4* i
t4 = b[t3] /*compute b[i] */
t5 = t2*t4
t6 = prod+t5
prod = t6
t7 = i+1
i = t7
if i<=20 goto L1
• Three Address code of source code](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-10-2048.jpg)

![12
L1: t1 = 4* i
t2 = a[t1] /*compute a[i] */
t3 = 4* i
t4 = b[t3] /*compute b[i] */
t5 = t2*t4
t6 = prod+t5
prod = t6
t7 = i+1
i = t7
if i<=20 goto L1
prod = 0
i = 1
Block B1
Block B2
• One node is distinguished as the initial node (B1).
• There is a directed edge B1 → B2, if B2 can
immediately follow B1 in some execution sequence;
i.e.,
• There is a conditional or unconditional jump
from the last statement of B1 to the first
statement of B2, or
• B2 immediately follows B1. so there is an edge
from B1 (last statement) to B2 (first
statement), and B1 does not end in an
unconditional jump.
• B1 is the predecessor of B2, and B2 is a
successor of B1.
CONTROL FLOW GRAPH (CFG)](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-12-2048.jpg)









![Algebraic Simplification
• Use algebraic properties to simplify expressions
• Some expressions can be simplified by replacing them with an equivalent expression that is more efficient.
22
-(-i) i
Example:
The code fragment below contains expressions that can be simplified.
void f (int i)
{
a[0] = i + 0;
a[1] = i * 0;
a[2] = i - i;
a[3] = 1 + i + 1;
}
Below is the code fragment after expression simplification.
void f (int i)
{
a[0] = i;
a[1] = 0;
a[2] = 0;
a[3] = 2 + i;
}](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-22-2048.jpg)

![Copy Propagation
• Given an assignment x = y, replace later uses of x with uses of y, provided there are no
intervening assignments to x or y.
• Example
x[i] = a; x[i] = a;
sum = x[i] + a; sum = a + a;
• Example
x := y; s := y * f(y)
s := x * f(x)
24
After y is assigned to x, use y to replace x till x is assigned again reduce the copying.
If y is reassigned in between, then this action cannot be performed.](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-24-2048.jpg)





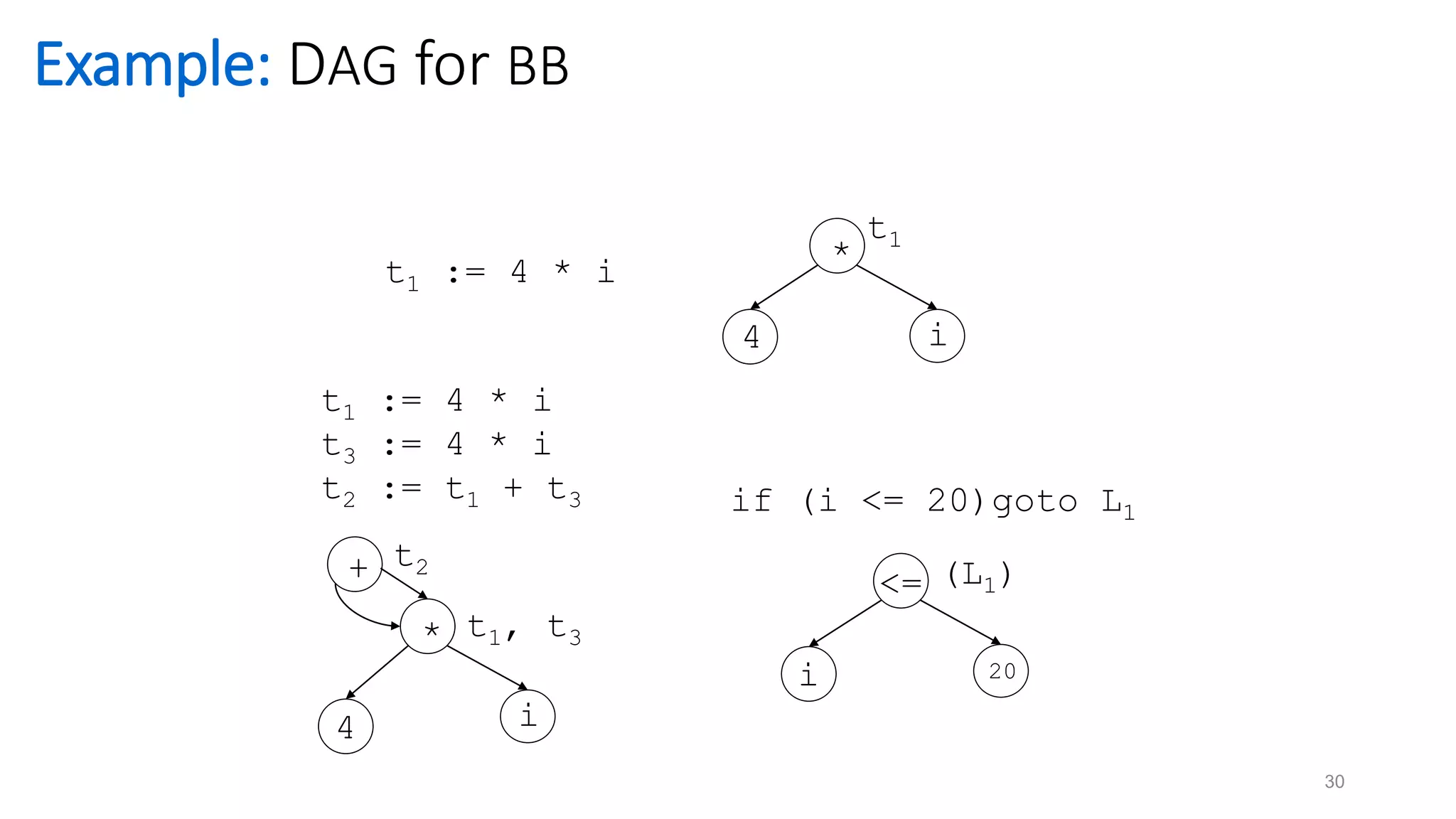

![Algorithm:
For each 3AC, A in BB
if A is any of the following forms:
1. x = y op z
2. x = op y
3. x = y
1. if ((ny = node(y)) == undef)
ny = Create (y);
if (A = = type 1) and ((nz = node(z)) == undef)
nz = Create(z);
32
Construction of DAGs for BB
2. If (A = = type 1) //x = y op z
Find a node labelled ‘op’ with left and right as ny and nz respectively [determination of common sub-expression]
If (not found)
n = Create (op, ny, nz);
If (A = = type 2) //x = op y
Find a node labelled ‘op’ with a single child as ny
If (not found)
n = Create (op, ny);
If (A = = type 3) n = Node (y); //x = y
2. Remove x from Node(x).list
Add x in n.list
Node(x) = n;](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-32-2048.jpg)
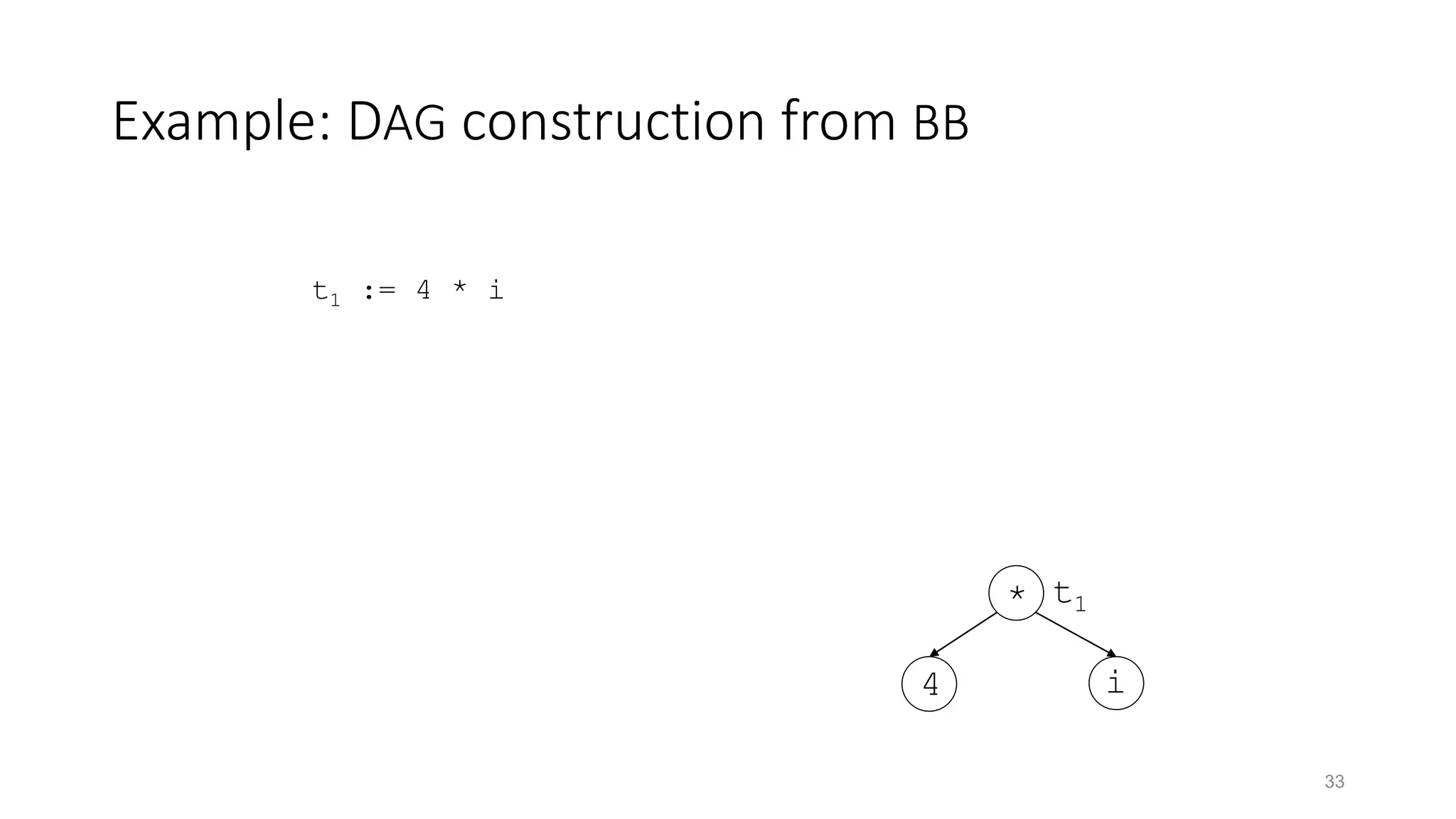
![Example: DAG construction from BB
34
t1 := 4 * i
t2 := a [ t1 ]
*
i
4
t1
[]
a
t2](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-34-2048.jpg)
![Example: DAG construction from BB
35
t1 := 4 * i
t2 := a [ t1 ]
t3 := 4 * i
*
i
4
t1, t3
[]
a
t2](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-35-2048.jpg)
![Example: DAG construction from BB
36
t1 := 4 * i
t2 := a [ t1 ]
t3 := 4 * i
t4 := b [ t3 ]
*
i
4
t1, t3
[]
a
t2
[]
b
t4](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-36-2048.jpg)
![Example: DAG construction from BB
37
t1 := 4 * i
t2 := a [ t1 ]
t3 := 4 * i
t4 := b [ t3 ]
t5 := t2 + t4
*
i
4
t1, t3
[]
a
t2
[]
b
t4
t5
+](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-37-2048.jpg)
![Example: DAG construction from BB
38
t1 := 4 * i
t2 := a [ t1 ]
t3 := 4 * i
t4 := b [ t3 ]
t5 := t2 + t4
i := t5
*
i
4
t1, t3
[]
a
t2
[]
b
t4
t5,i
+
• Observations:
• A leaf node for the initial value of an id
• A node n for each statement s
• The children of node n are the last definition (prior to s) of the operands of n](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-38-2048.jpg)
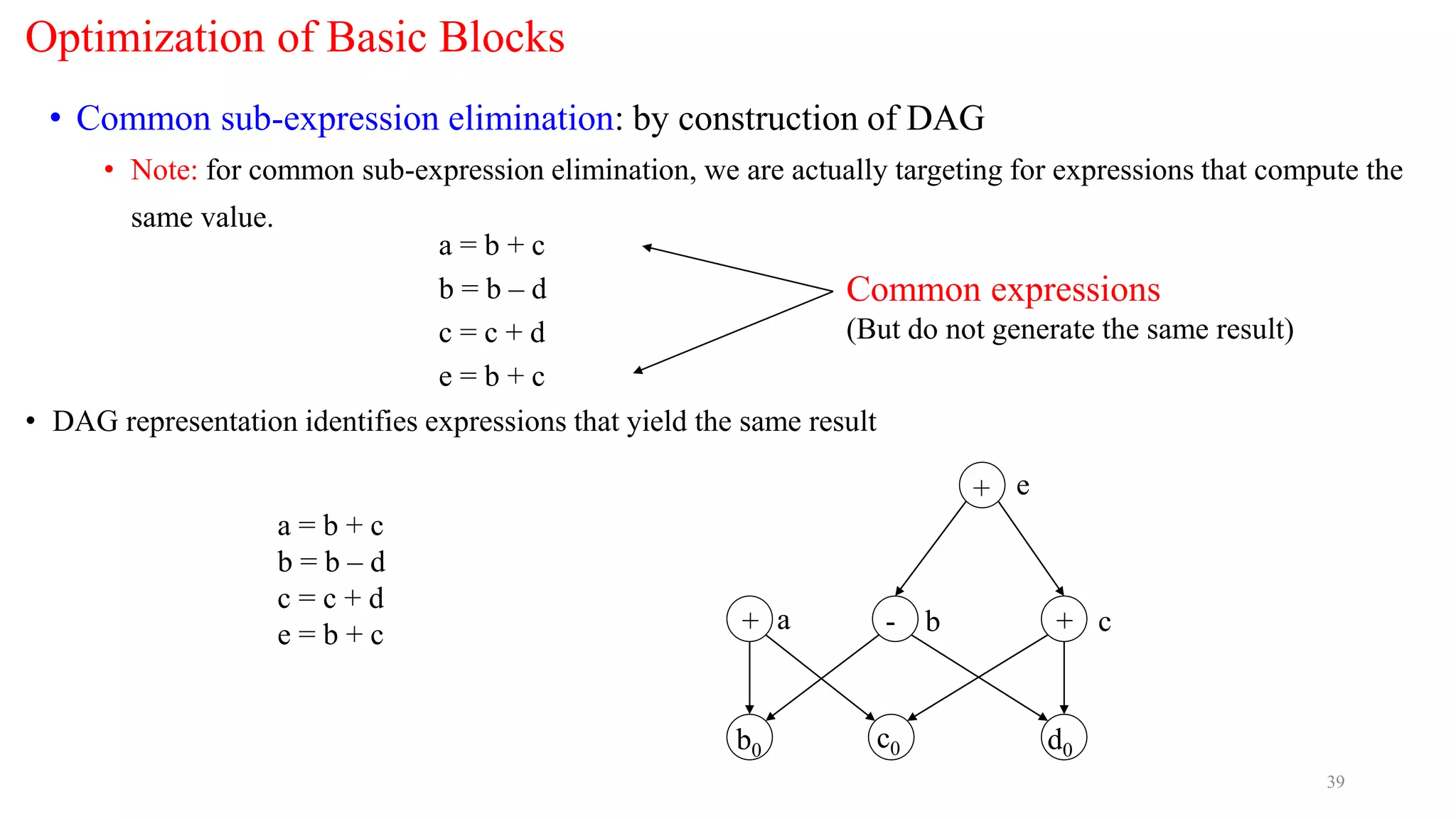
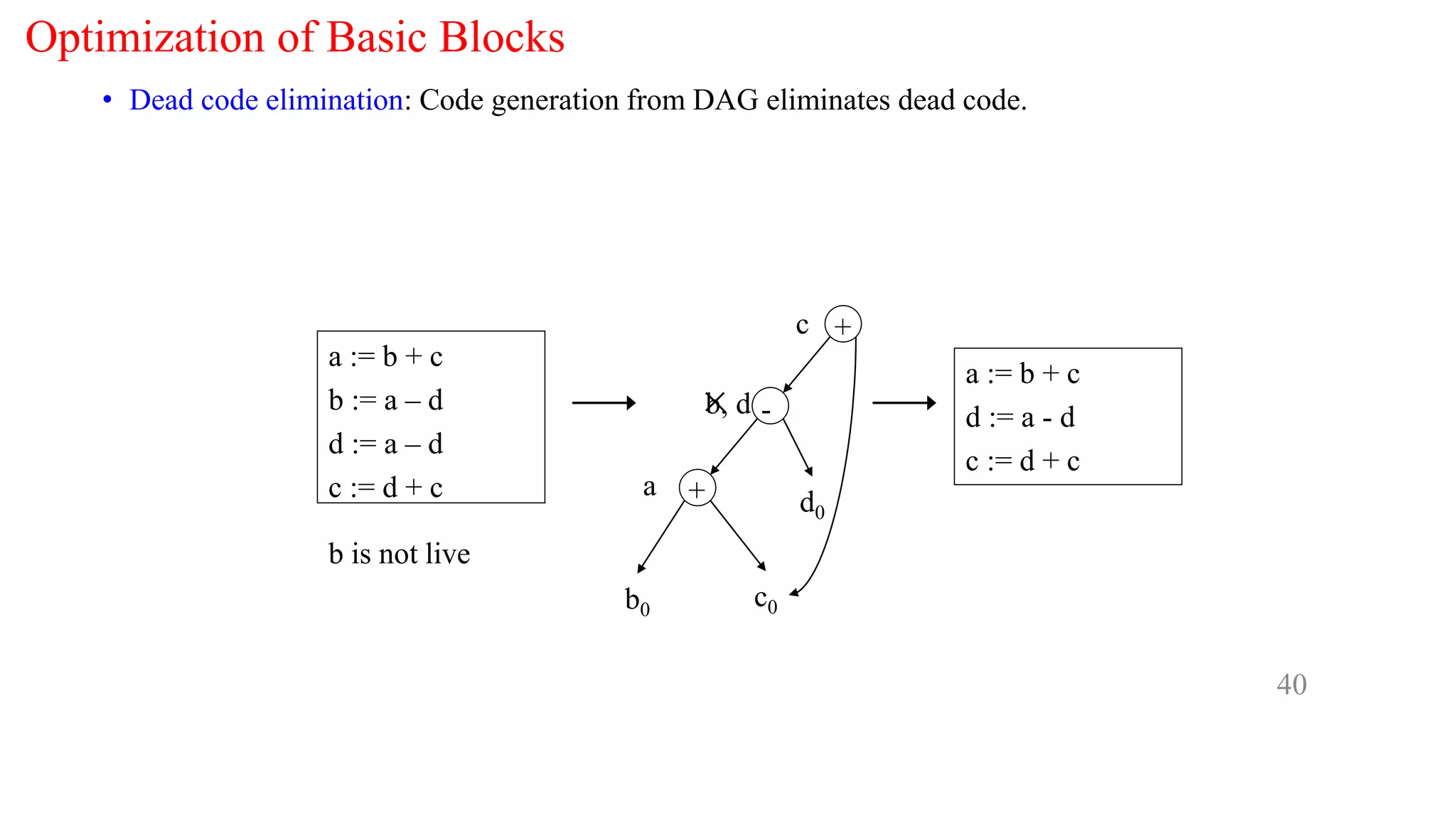










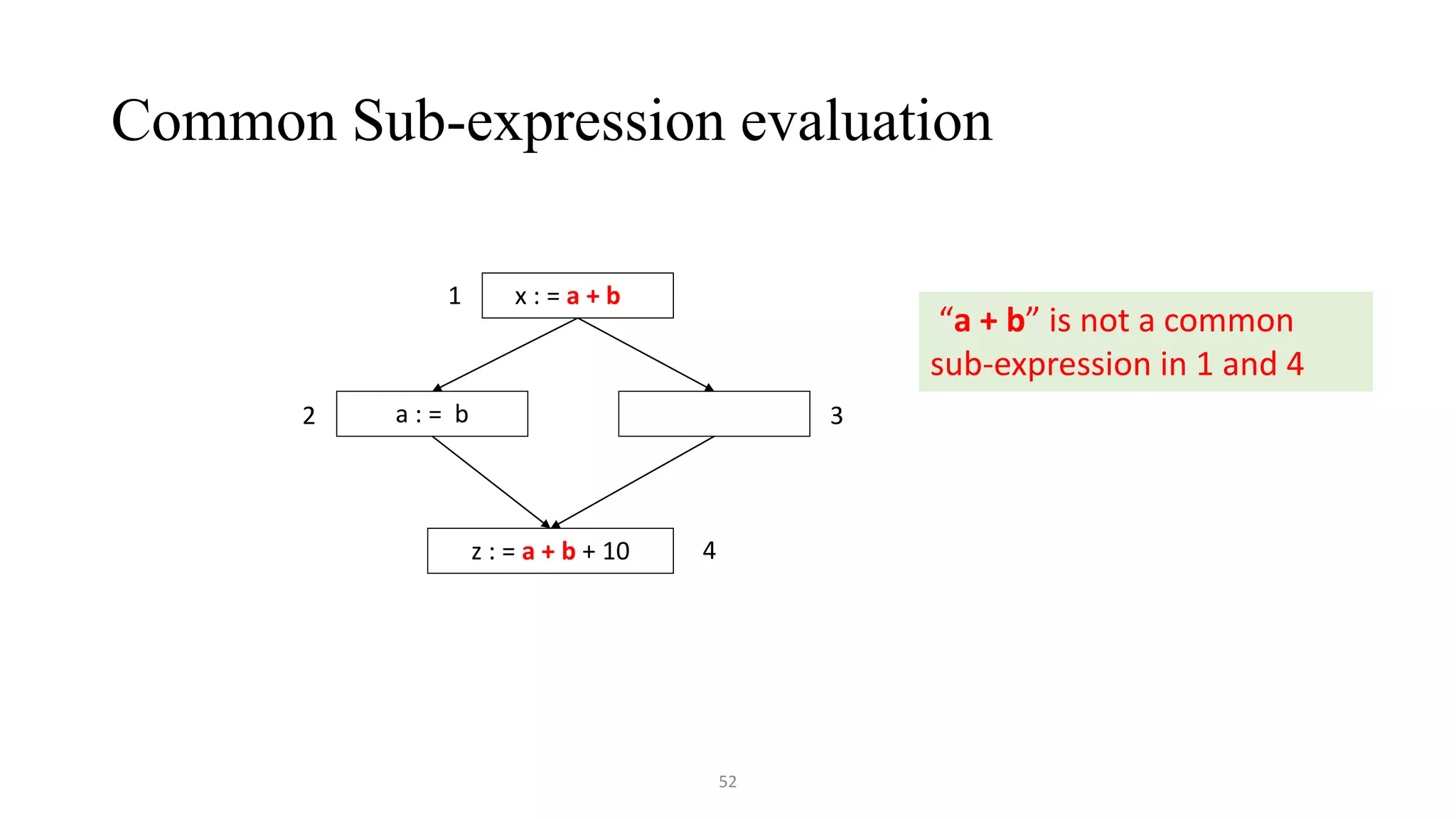
![Common Sub-expression elimination
• Common sub-expression elimination
• Example 1:
a := b + c a := b + c
c := b + c c := a
d := b + c d := a
• Example 2: in array index calculations
• c[i+1] := a[i+1] + b[i+1]
• During address computation, i+1 should be reused
• Not visible in high level code, but in intermediate code](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-51-2048.jpg)





![• Example
for (i=0; i<n; i++)
a[i] = a[i] + x/y;
• Three address code
for (i=0; i<n; i++)
{
c = x/y;
a[i] = a[i] + c;
}
c = x/y;
for (i=0; i<n; i++)
a[i] = a[i] + c; 58
Code Motion - Loop Optimization](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-58-2048.jpg)

![Induction variable elimination
• If there are multiple induction variables in a loop, can eliminate the ones which are used only in
the test condition
60
The code fragment below has three induction
variables (i1, i2, and i3) that can be replaced
with one induction variable
int a[SIZE];
int b[SIZE];
void f (void)
{
int i1, i2, i3;
for (i1 = 0, i2 = 0, i3 = 0; i1 < SIZE; i1++)
a[i2++] = b[i3++];
return;
}
The code fragment below shows the loop
after induction variable elimination.
int a[SIZE];
int b[SIZE];
void f (void)
{
int i1;
for (i1 = 0; i1 < SIZE; i1++)
a[i1] = b[i1];
return;
}](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-60-2048.jpg)

![Loop Fusion - Loop Optimization
• Example
for (i=0; i<n; i++) {
A[i] = B[i] + 1
}
for (i=0; i<n; i++) {
C[i] = A[i] / 2
}
for (i=0; i<n; i++) {
D[i] = 1 / C[i+1]
}
Before Loop Fusion
for (i=0; i<n; i++) {
A[i] = B[i] + 1
C[i] = A[i] / 2
D[i] = 1 / C[i+1]
}
Is this correct?
Actually, cannot fuse the third loop
for (i=0; i<n; i++) {
A[i] = B[i] + 1
C[i] = A[i] / 2
}
for (i=0; i<n; i++) {
D[i] = 1 / C[i+1]
}](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-62-2048.jpg)

![Loop unrolling or Loop collapsing - Loop Optimization
64
Example:
In the code fragment below, the double-nested loop on i and j can be collapsed into a single-nested loop.
int a[100][300];
for (i = 0; i < 300; i++)
for (j = 0; j < 100; j++)
a[j][i] = 0;
Here is the code fragment after the loop has been collapsed.
int a[100][300];
int *p = &a[0][0];
for (i = 0; i < 30000; i++)
*p++ = 0;](https://image.slidesharecdn.com/codeoptimization-techniques-210308114603/75/Code-optimization-in-compiler-design-64-2048.jpg)

