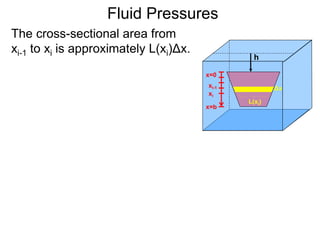
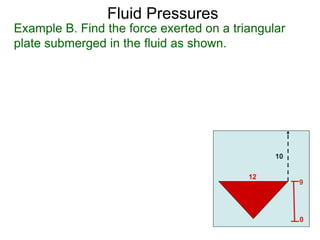
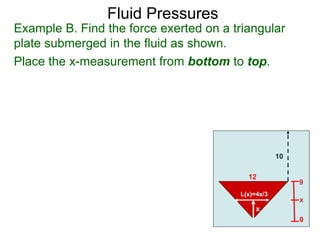
The document discusses calculating the force exerted on plates submerged in fluids. It explains that the force is calculated by dividing the plate into thin strips, determining the cross-sectional area and depth of each strip, and taking the limit of the sum as the widths approach zero. This gives an integral representing the total force as the density of the fluid multiplied by the cross-sectional length times the depth integrated over the length of the plate. Examples are presented to demonstrate calculating the force on specific shapes, such as a square plate, triangular plate, and semi-circular plate.





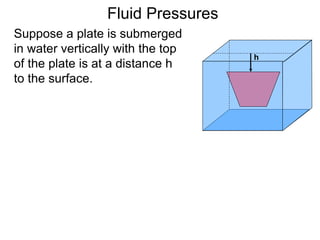
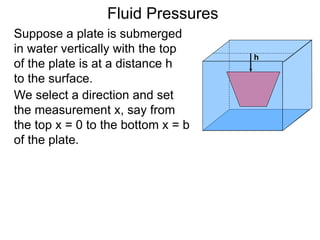
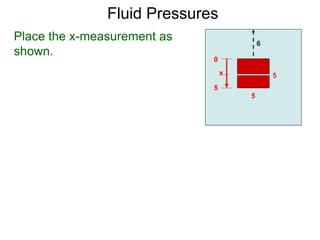
![Suppose a plate is submerged
in water vertically with the top
of the plate is at a distance h
to the surface.
h
We select a direction and set
the measurement x, say from
the top x = 0 to the bottom x = b
of the plate.
x=0
x=b
xi-1
xi
Let the sequence {0=x0, x1, x2, .. , xn=b} be an equi-
partition of [0, b] and xi–1 and xi be two consecutive
points.
Fluid Pressures](https://image.slidesharecdn.com/9fluidpressures-x-190130063646/85/10-fluid-pressures-x-10-320.jpg)
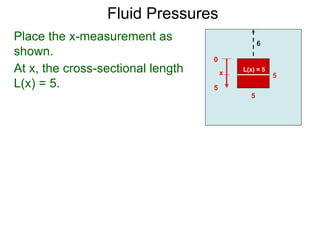
![Suppose a plate is submerged
in water vertically with the top
of the plate is at a distance h
to the surface.
h
We select a direction and set
the measurement x, say from
the top x = 0 to the bottom x = b
of the plate.
x=0
x=b
xi-1
xi
Let L(x) = cross-sectional length at x, so
L(xi) = cross-sectional length at xi.
Let the sequence {0=x0, x1, x2, .. , xn=b} be an equi-
partition of [0, b] and xi–1 and xi be two consecutive
points.
Fluid Pressures
L(xi)](https://image.slidesharecdn.com/9fluidpressures-x-190130063646/85/10-fluid-pressures-x-11-320.jpg)
![Suppose a plate is submerged
in water vertically with the top
of the plate is at a distance h
to the surface.
h
We select a direction and set
the measurement x, say from
the top x = 0 to the bottom x = b
of the plate.
x=0
x=b
xi-1
xi
Let L(x) = cross-sectional length at x, so
L(xi) = cross-sectional length at xi.
Let the sequence {0=x0, x1, x2, .. , xn=b} be an equi-
partition of [0, b] and xi–1 and xi be two consecutive
points.
Let Δx = the length of each subinterval.
Fluid Pressures
L(xi)
Δx](https://image.slidesharecdn.com/9fluidpressures-x-190130063646/85/10-fluid-pressures-x-12-320.jpg)