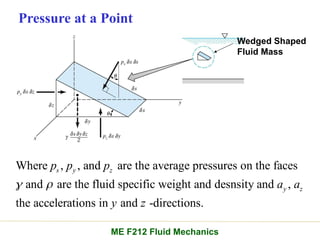
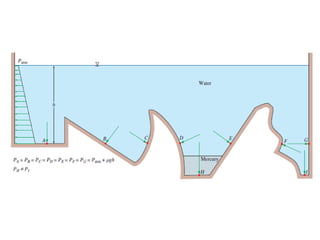
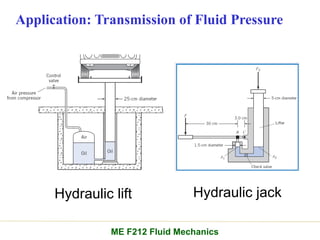
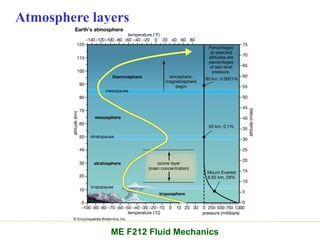
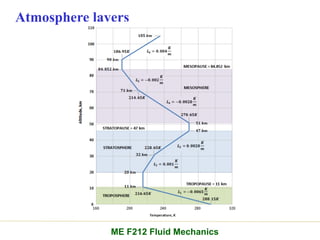
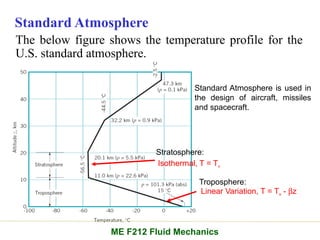
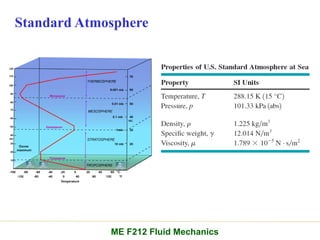
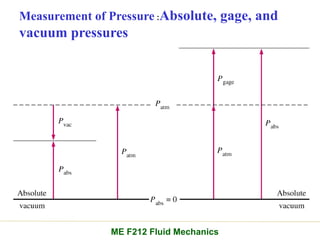
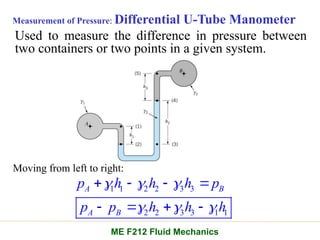
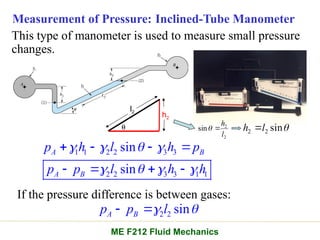
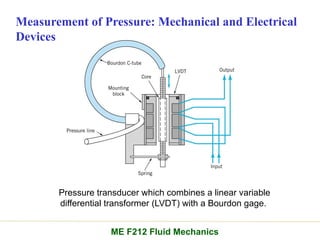
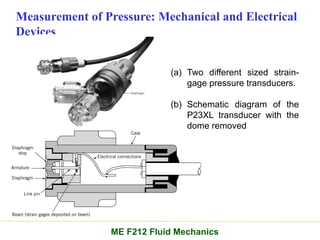
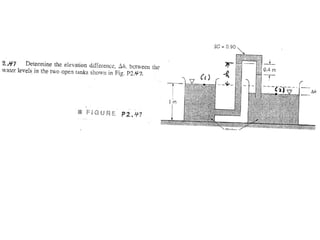
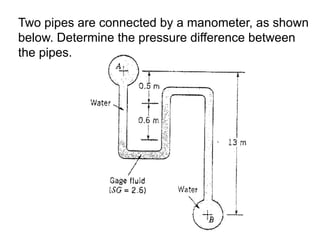
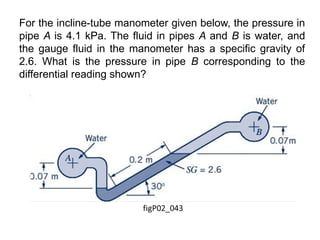
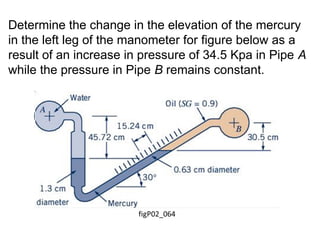
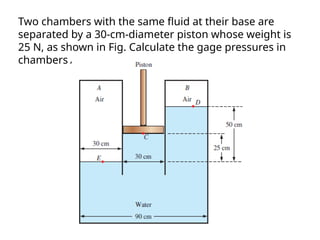
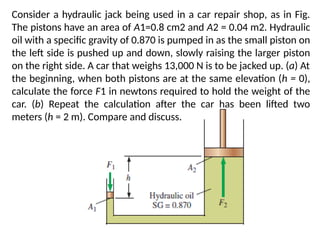
Chapter 2 of the fluid statics lecture discusses the determination of pressure at a point in a fluid at rest, incorporating concepts such as manometers, hydrostatic forces, and buoyant forces. It emphasizes Pascal's law, which states that pressure at a point is independent of the orientation of the plane, and explores equations related to pressure variation in fluids with applications in hydraulic systems. Additionally, the chapter reviews standard atmospheric conditions and methods for measuring pressure, including the use of barometers and manometers.