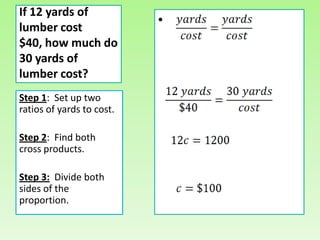
Here are the key steps to solve proportion word problems: 1. Identify the quantities given in the problem and set up a proportion relating the quantities. 2. Set up the cross products of the proportion and set them equal to each other. 3. Isolate the unknown quantity by dividing or multiplying both sides of the equation by the appropriate term. 4. Simplify and solve for the unknown quantity. Check that the units make sense. The proportion allows you to relate known quantities to unknown quantities when the quantities are in a constant ratio. Setting up the cross products properly and then isolating the unknown through mathematical operations will allow you to solve for what you need.

1. • 1. Discuss Fractions “Quiz” with your table
• 2. Intro to Ratio and Proportion
• 3. Setting Up Ratios
• 4. Proportion
• 5. Proportion Word Problems

2.  A ratio is a comparison of numbers by
division.
 A ratio can be written with the word to, with
a colon (:), or as a fraction.
 Should always be reduced (simplifying)

3. 3 to 2 3:2

4.  The numbers in a ratio MUST be written
in the order the problem asks for.
 Always reduce a ratio to lowest terms.
 When a ratio is an improper
fraction, DO NOT change it to a mixed
number.

5.  1. Read the problem carefully.
 2. Pay attention to the order the question
wants you to write the ratio.
 3. Set up the ratio appropriately.
 4. REDUCE!!!!!

6.  Evelyn earns $2400 a month. She pays $600 a
month in rent. What is the ratio of her
income to her rent.
Make a ratio with her income first (in the
numerator) and her rent second.
income 2400 24 4 For every $4 she makes,
rent 600 6 1 She spends $1 on rent

7.  In a factory, there are 150 men and 100
women working.
To compare these facts, write a ratio of men to
women working in the factory.
men 150 15 3 men
women 100 10 2 women

8.  1. 24:30 =
200:125 =
28 =
21

9.  2. 3.4 =
1.7
4 to 1000 =
$560 to $320

10.  3.Alvaro makes $600 a week and
saves $60 a week. What is the ratio
of the amount he makes to the
amount he saves?

11.  4. For Alvaro, in problem
3, what is the ratio of the
amount he saves to the
amount he makes?

12.  5. There are 24 students in Sam’s English
class. Four of the students speak Armenian
as a first language. What is the ratio of
Armenian speakers to the total number of
students in the class?

13.  6. Anna drove 110 miles on 22 gallons
of gas. What is the ratio of the distance
she drove to the number of gallons of
gas she used?

14. When you are not given
both numbers you
need, you may have to
determine one of the
numbers.

15.  On a test with 20 problems, Maceo got 2
problems wrong. What was the ratio of the
number of problems he got right to the total
number of problems?
Step 1: Find the number
of problems he got right. 20-2= 18problems right.
Step 2: Make a ratio of right 18 9
the number of problems
total 20 10
he got right to the total
number of problems.
Reduce.

16.  1. A GED class of 20 students has 12 women.
 A.) What is the ratio of the number of
women to the total number of students?
 B.) What is the ratio of the number of men
to the total number of students?
 C.) What is the ratio of the number of men
to the number of women?
 D.) What is the ratio of the number of
women to the number of men?

17.  2. At Baxter Electronics there are 105 union
workers and 45 nonunion workers.
 A.) What is the ratio of the number of union
workers to the total number of workers?
 B.) What is the ratio of the number of nonunion
workers to the total number of workers?
 C.) What is the ratio of the number union
workers to the number of nonunion workers?
 D.) What is the ratio to the number of workers
to the number of union workers?

18.  From a total yearly budget of
$18,000,000, the city of McHenry
spends $3,000,000 on education. What
is the ratio of the amount spent on
education to the amount not spent on
education?

19.  4. A math test of 50 questions included
15 fraction problems and 5 decimal
problems. What is the ratio of the total
number of fraction and decimal
problems to the number of questions
on the test?

20.  5. There are 1213 registered voters in
Paul’s village. During the last election
887 people actually voted. Which of
the following is approximately the ratio
of the number of people who voted to
the total number of registered voters?

21. • A statement that says two ratios (or two
fractions) are equal.
Proportion Statements
2:4 = 1:2

22. • Remember: cross products of equal fractions
are equal
4=4

23. • Each of the four numbers in a proportion is
called an ELEMENT or a TERM.
• A letter usually represents the missing term.

24. • Step 1: Write a statement with two equal
cross products.
• Step 2: Divide both sides of the statement by
the number in front of the missing term.
=

25. • Solve for c in
• Step 1: Write a
statement with two
equal cross products.
• Step 2: Divide both
sides of the statement
by the number in front
of the missing term.

26. • Solve for y in the proportion
5:y=2:8
• Step 1: Write a
statement with two
equal cross products.
• Step 2: Divide both
sides of the statement
by the number in front
of the missing term.

27. If 12 yards of
lumber cost
•
$40, how much do
30 yards of
lumber cost?
Step 1: Set up two
ratios of yards to cost.
Step 2: Find both
cross products.
Step 3: Divide both
sides of the
proportion.

28. Carlos got 2 problems •
wrong for every 5 problems
right on a test. How many
problems did Carlos get
wrong if there were 35
problems on the test?
• Step 1: Set up two
ratios of wrong to total
• Step 2: Find both cross
products.
• Step 3: Divide both
sides of the proportion.

29. The ratio of the number of
men to the number of
•
women working in the
county hospital is 2:3. If
480 women work in the
hospital, how many men
work there?
• Step 1: Set up two
ratios of ________to
________.
• Step 2: Find both cross
products.
• Step 3: Divide both
sides of the proportion.

30. Manny Drove 110 miles in
2 hours. Which •
expression shows the
distance he can travel in 5
hours if he drives at the
same speed?
• Step 1: Set up two
ratios of ________to
________.
• Step 2: Find both
cross products.
• Step 3: Divide both
sides of the
proportion.