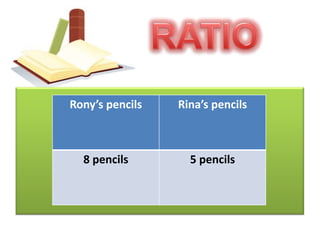
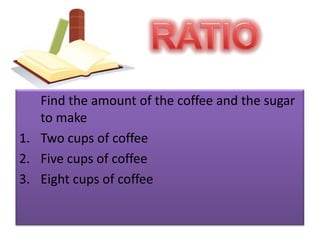
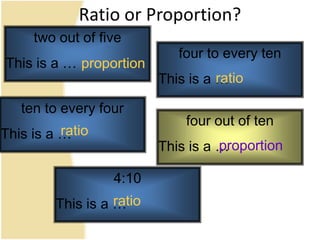
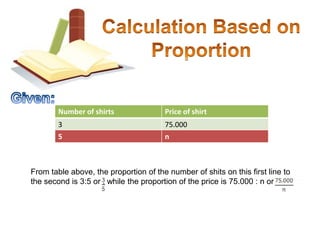
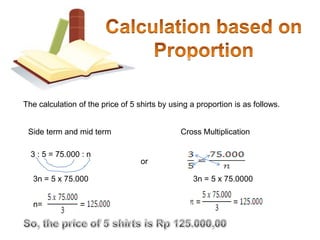
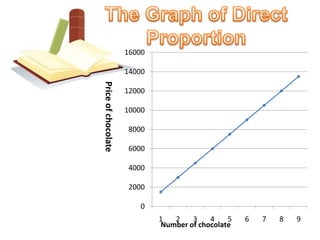
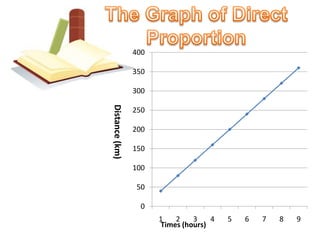
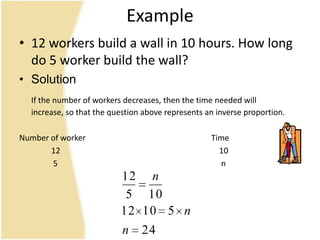
The document discusses ratio, proportion, and scaled drawings. It begins by defining ratio as comparing two quantities through difference or division. It provides examples of using ratios to compare ages and weights. It then defines proportion as two ratios set equal to each other. Examples of direct and inverse proportions are given. Scaled drawings are defined as pictures made to represent real objects at a certain scale. Factors of enlargement and reduction in scaled drawings are also discussed.

1. Ratio and ProportionNurinaAyuningtyasWahyuFajarYan AdityaYola Yaneta

2. Ratio and ProportionDo they same?What’s the differ among them? LET’S CHECK THIS OUT!!!!

3. Let’s us learn deeply aboutRatio & Proportion!!!

4. RatioWe often encounter things ralated to ratios in daily life, for example:Tony’s age is greater than Rudy’sRony’s weight is twice of Rino’sThe area of Mr.Mike’s field is larger than Mr.Samiden

5. RatioComparing two quantities or more can be performed by two methods., nemely : through difference and division (quotient). For example: Ryo’s age is 18 years and Tyo’s age is 6 years old. Their age can be compared in two methods, namely:

6. RatioACCORDING TO THE DIFFERENCE Ryo’s age is 12 years older than Tyo’s age, or Tyo’s age is 12 years younger than Ryo’s age. In this case, the ratio of both children’s ages is done by finding the difference, namely: 18 – 6 = 12

7. RatioB. ACCORDING TO DIVISION Ryo’s age is three times of Tyo’s age. In this case, the ratio of both children’s ages is done by finding the quotient , namely: 18 : 6 = 3

8. RATIOComparing Two Quantities of the Same Kind One day Rony and Rina go to shop to buy some pencils. They went at morning, the buy some pencils for a test tomorrow. Rony bought 8 pencils and Rina bought 5 pencils. Now they have 13 pencils to preparing test at tomorrow.

9. RATIOFrom the story above ,answer the question below!!!How many pencils does Rony have?How many pencils does Rina have?Record the result on a table!

10. RATIO

11. RATIOFrom the table, we can say that the ratio of Rony’s book to Rina’s book is 8 : 5From the table, we can say that the ratio of Rina’s book to Rony’s book is 5 : 8

12. RATIOTo make a cup of coffee, 2 teaspoons of coffee and 3 teaspoons of sugar are needed. Find the ratio of the coffee to the sugar to make a cup of coffee.The ratio is 2 : 3

13. RATIO Find the amount of the coffee and the sugar to make Two cups of coffeeFive cups of coffeeEight cups of coffee

14. RATIOTwo cups of coffeeTo make a cup of coffee, the ratio of coffee to sugar is 2 : 3The sum of coffee and sugar that needed to make two cups of coffee isCups of coffee times the ratio.2 x 2 teaspoons of coffee = 4 teaspoons2 x 3 teaspoons of sugar = 6 teaspoons It means that the sum of coffee is 4 teaspoons and the sum of sugar is 6 teaspoons

15. RATIOFive cups of coffeeTo make a cup of coffee, the ratio of coffee to sugar is 2 : 3The sum of coffee and sugar that needed to make five cups of coffee isCups of coffee times the ratio.5 x 2 teaspoons of coffee = 10 teaspoons5 x 3 teaspoons of sugar = 15 teaspoons It means that the sum of coffee is 10 teaspoons and the sum of sugar is 15 teaspoons

16. RATIOEight cups of coffeeTo make a cup of coffee, the ratio of coffee to sugar is 2 : 3The sum of coffee and sugar that needed to make eight cups of coffee isCups of coffee times the ratio.8 x 2 teaspoons of coffee = 16 teaspoons8 x 3 teaspoons of sugar = 24 teaspoons It means that the sum of coffee is 16 teaspoons and the sum of sugar is 24 teaspoons

17. RATIOWe can conclude that RATIO is… two "things" (numbers or quantities in same unit) compared to each other.

18. SCALED DRAWING

19. SCALED DRAWINGWe often find scaled pictures or models as maps, ground plan of a building house and a model of a car or plane in daily life. The following are several examples of scaled pictures and models.

20. SCALED DRAWING

21. IlustrationFor example : a father ask his child to draw his rectangular land of 500m for long and 300 m wide. It’s imposibble to draw a piece of land in actual measurement, but congruent to its origin.1 cm represent 100 m so that 500m represented by 5 cm and 300m represented by 3 cm

22. What is the definition of scaled picture?

23. A scaled picture is a picture made to represent a real object or situation in a certain measure.With a scaled picture we know object or situation as a whole without watching the actual object.

24. For example the piece of land in the form of a rectangle 500 m long and 300 m wide is represented by a figure of a rectangle of 5 cm long and 3 cm wide as the figure below.3 cm5 cm

25. Can you find the scale?To find the scale we can compare between the model picture and the actual measurement.

26. Based on the explanation above, we can make the following ratio :

27. The Ratio between the measurement on the model picture and the actual measurement is called scale and formulated as follows

28. ExercisesA map is made to scale of 1 : 200.000, find :The actual distance if the distance on the map is 5 cm.The distance on the map if the actual distance is 120 km.Given on the map that the distance of two towns is 4 cm, while the actual distance is 160 km, Find the scale of the map!

29. ExercisesAnswer :30 km60 cm1 : 4.000.000

30. Factor of Enlargement and Reduction on Scaled Picture and ModelWhat is the factor of Enlargement and Reduction on Scaled Picture and Model?

31. Factor of Enlargement and Reduction on Scaled Picture and ModelWhat the purpose of this?A very small object can be seen and learned easily if it is enlarged by picture using a certain scale.And the very big object can be reducted by picture using certain scale

32. For example :A rectangle have long 2 cm and width 1 cm. In order to be clearly seen, the componens is enlarged three times. Length = 2 cm x 3 = 6 cmWidth = 1 cm x 3 = 3 cm1 cm3 cm2 cm6 cm

33. The ratio before and after enlargement :1 cm3 cm2 cm6 cm

34. 1 cm3 cm2 cm6 cmThe enlargement in the example above has a factor of scale 3 orBoth have the ratio 3 : 1. It means that all measurement on the shape the product of enlargement represents 3 times of the actual shape.

35. Story6 cm2 cm4 cm3 cm A photo have long 3 cm and width 2 cm.Because there are something, the photo’s size become 6 cm of length, 4 cm of width.

36. What is your 6 cm2 cm4 cm3 cmWhat is the happen of before and after?What is your conclution?What is the enlargement of this picture?

37. ConclutionFactor of scale where k>1 is called factor of enlargement

38. Story60 cm20 cm2 m6 m A bus have long 6 m and width 2 m. If someone want to make a model of bus, so the model of bus made of 60 cm length and 20 cm width.

39. What you see? What is the reduction of bus and this model?What is your conclution?

40. ConclutionFactor of scale where 0<k<1 is called factor of reduction

41. ExercisesA photograph of 4 cm high and 3 cm wide is enlarged in such away that its width is 6 cm. Find :The factor of scaleThe height after enlargmentRatio of area before and after enlargement

42. ExercisesFactor of scale = So the factor of scale is 2 or 2:1The height after enlargement = Factor of scale x the height of photograph = 2 x 4 = 8 cm

43. Exercisesc. Ratio of the photograph area before and after enlargement

44. Proportion

45. Proportion

46. Proportion

47. Proportion

48. ProportionOlit buys 2 books that have cost $8. If she wants to buy 6 books, how much does it cost she must to pay? So, Olit need to pay $ 24 for six books.Then we can say it “8 dollars for 2 books" equals “24 dollars for 6 books".

49. Proportionis two ratios set to be equal to each other.

50. Ratioor Proportion?two out of five This is a …four to every ten This is a …proportionratioten to every four This is a …four out of tenThis is a …ratioproportion4:10 This is a …ratio

51. Ratio, Proportion or Fraction?3 Aremaniafans to every 2 Bonekmaniafans This is a …ratio9 girls out of 10 use soap This is a …proportion3 boys out of 10 use deodorant This is a …proportion

52. Direct ProportionAndi buys a pair of shorts at the price of Rp 15.000,00. The price for two shorts, 3 shorts, and so on can be seen on the following table:

53. Direct ProportionThe table above indicates that the more shorts Andi buys the more money he has to spend. But, the amount of price for each shorts is always the same on each line:

54. Direct ProportionHenceforth, the equation of the portion of the number of shorts and the portion of prices on two certain lines is always same.Example:The quotient of the ratios on the other two line is: So, the number of shorts and the price always increase or decrease at the same ratio, so that we say there is a direct proportion between the number of shorts and the price.

55. Direct ProportionTHERE’RE TWO METHODS TO CALCULATE A DIRECT PROPORTION:CALCULATION BASED ON UNIT VALUECALCULATION BASED ON PROPORTION

56. Calculation Based on Unit ValueA car can travel 180 km in 3 hours. How long does the car need to travel 240 km? The time for 180 km = 3 jam

57. The time for 1 km =

58. The time to travel 240 km = x 240 = 4 hoursCalculation Based on ProportionGiven:From table above, the proportion of the number of shits on this first line to the second is 3:5 or , while the proportion of the price is 75.000 : n or

59. Calculation based on Proportion The calculation of the price of 5 shirts by using a proportion is as follows. Side term and mid termCross Multiplication3 : 5 = 75.000 : nor3n = 5 x 75.0003n = 5 x 75.0000n= So, the price of 5 shirts is Rp 125.000,00

60. Calculation Based on ProportionBased on the example above, on direct proportion, it is valid:If a : b = c : d, hence ad = bcIf , hence ad = bc

61. practiceThe price of three meters of cloth is Rp 54.000,00. How many maters of cloth is obtained by Rp 144.000,00?The price of 3 kg of apples is Rp 36.000,00. What is the price of 15 kg of apples?

62. SolutionThe price of 3 meters of cloth = Rp 54.000,00 The price of 1 meter of cloth = With Rp 144.000 we can obtain So, we can obtain 8 meters of cloth.If the number of apples increase, hence the price also increase. It means that the question above represent a direct proportion, Number of apples (kg) Price (rupiah) 3 36.000 15 So, the price of 15 kg of apples is Rp 180.000,00

63. The Graph of Direct ProportionIn order that you know the graph of a direct proportion, consider the following description. The table below indicates a relation between the number of chocolate and the price.

64. The Graph of Direct Proportion

65. The Graph of Direct Proportion PracticeComplete the table above!Make its graph using the same scale!Based on the graph, calculate the distance taken in 2 and a half!

66. The Graph of Direct Proportion

67. The Graph of Direct ProportionSolution of c. The distance for 1 hour = 40 km

68. The distance for 2 hour and a half = x 40 km = 100 kmInverse ProportionINVERSE PROPORTION

69. Review : In direct proportions, when one row of a table shows that the proportion gets larger, the numbers in the other row or rows get "proportionally" larger.But, it’s different with inverse proportion. In these proportions, one row gets smaller at the same time that another gets larger.

70. Application of Inverse ProportionThe speed of Car A is 60 cm/sec. It needs 3 second to go until finish.The speed of Car B is 30 cm/sec. It needs 6 second to go until finish.So, which one the fastest???? Why???

71. The proportional quotient of the average speed and time proportion on two certain lines always represent multiplication inverse of each.2 is the inverse of ½

72. Example12 workers build a wall in 10 hours. How long do 5 worker build the wall?SolutionIf the number of workers decreases, then the time needed will increase, so that the question above represents an inverse proportion.Number of worker Time 12 10 5 n