Download to read offline
Uploaded byPooja M
MATH - RATIO (CLASS V)
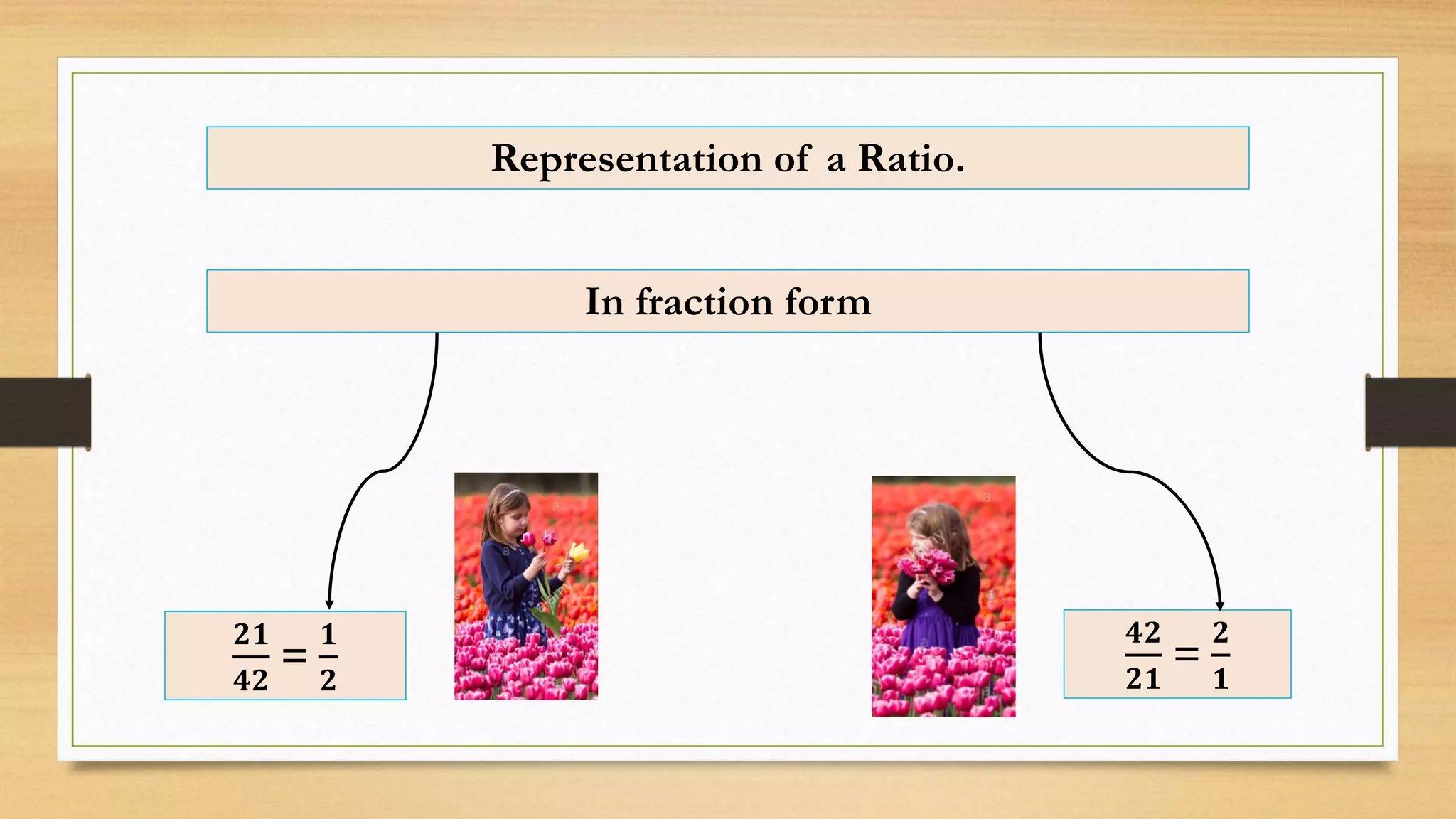
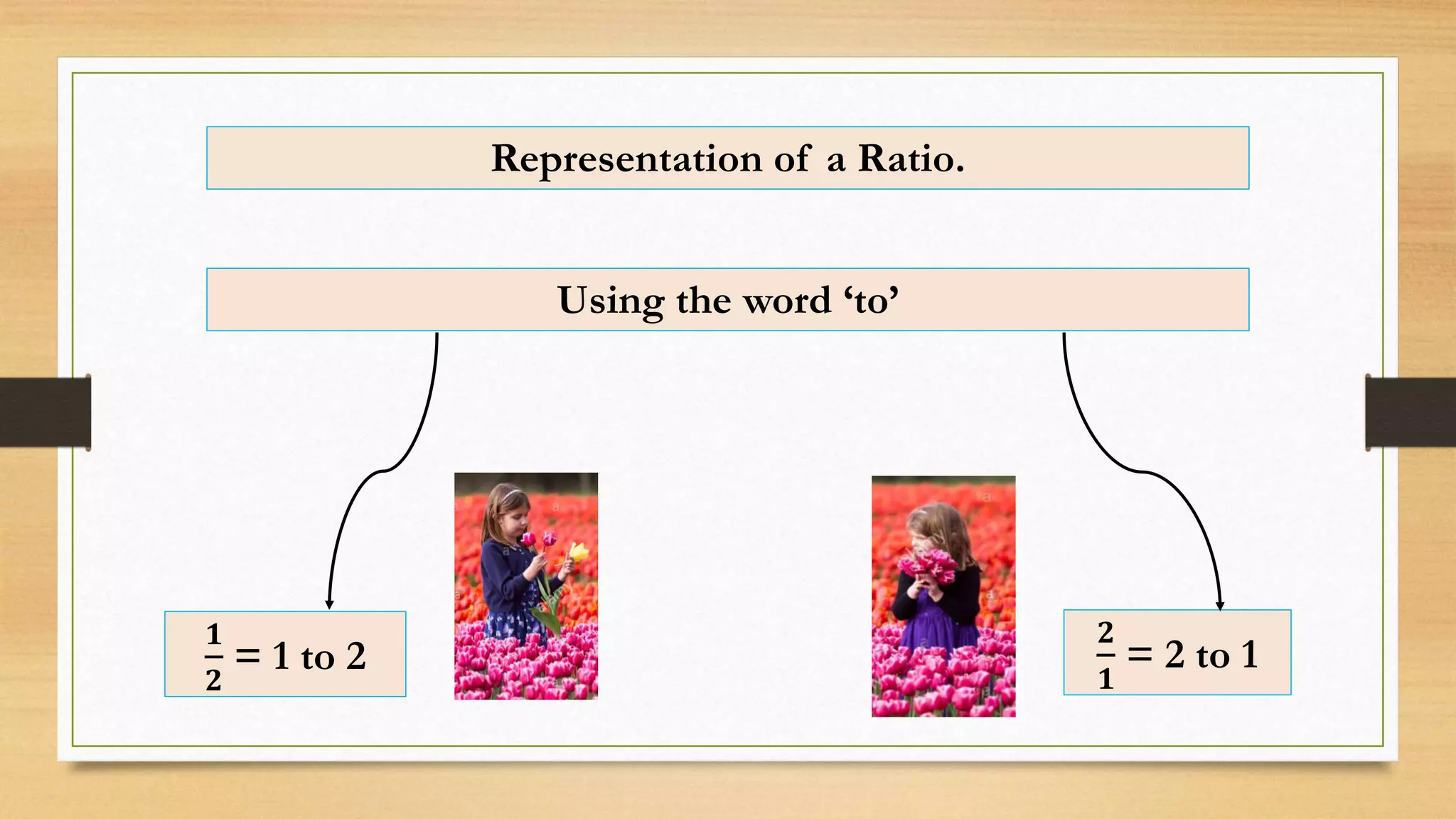
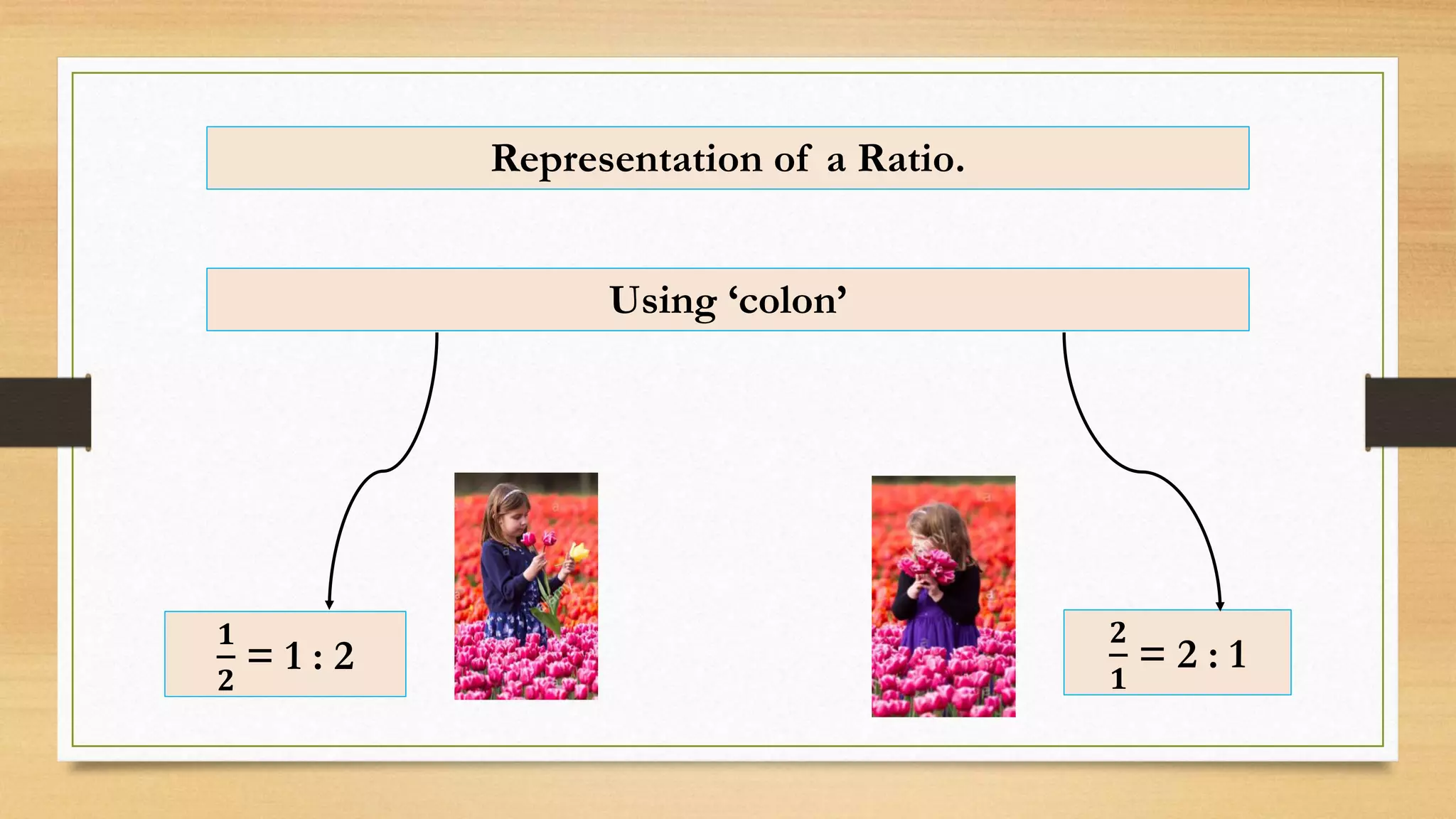
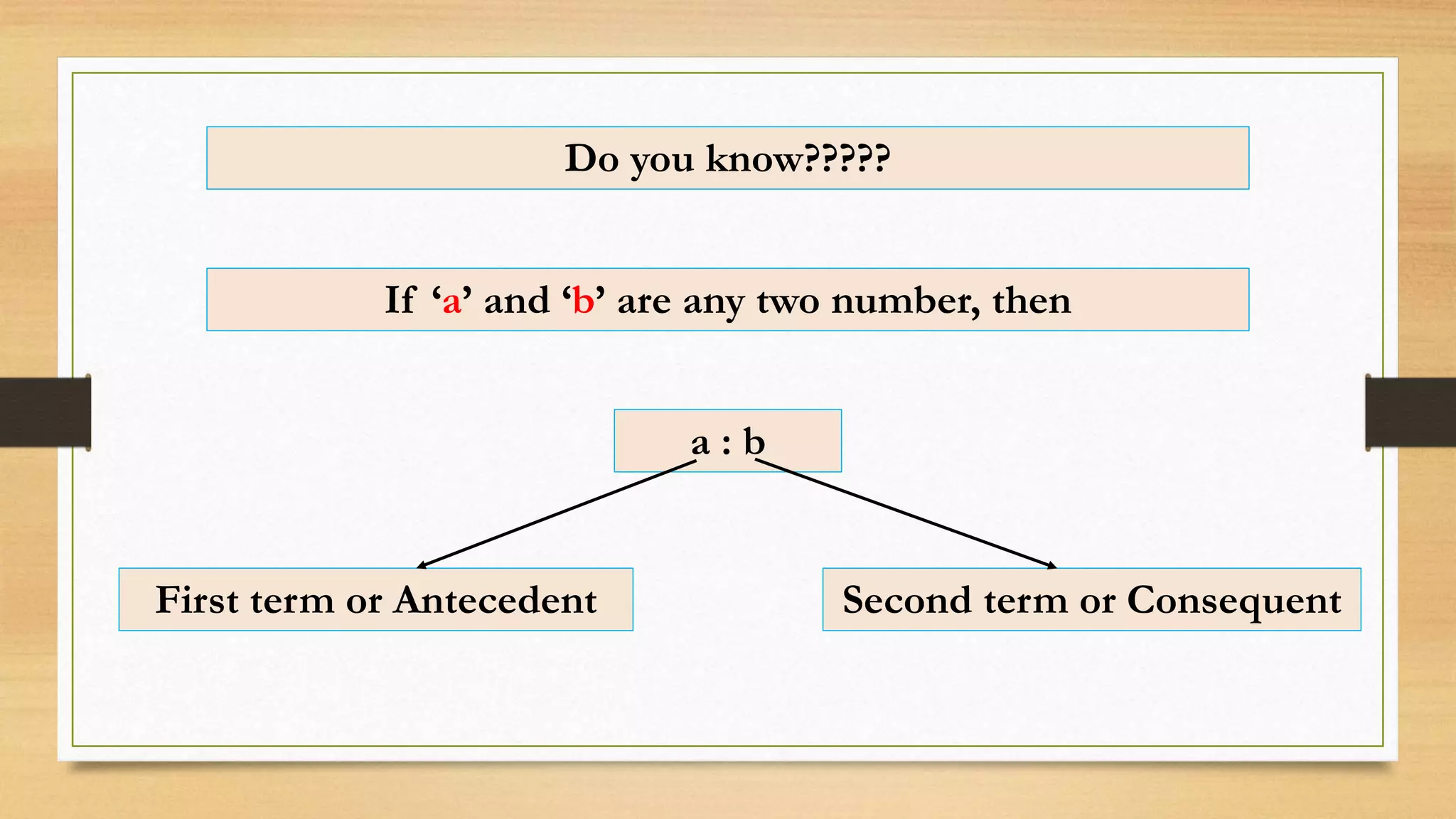
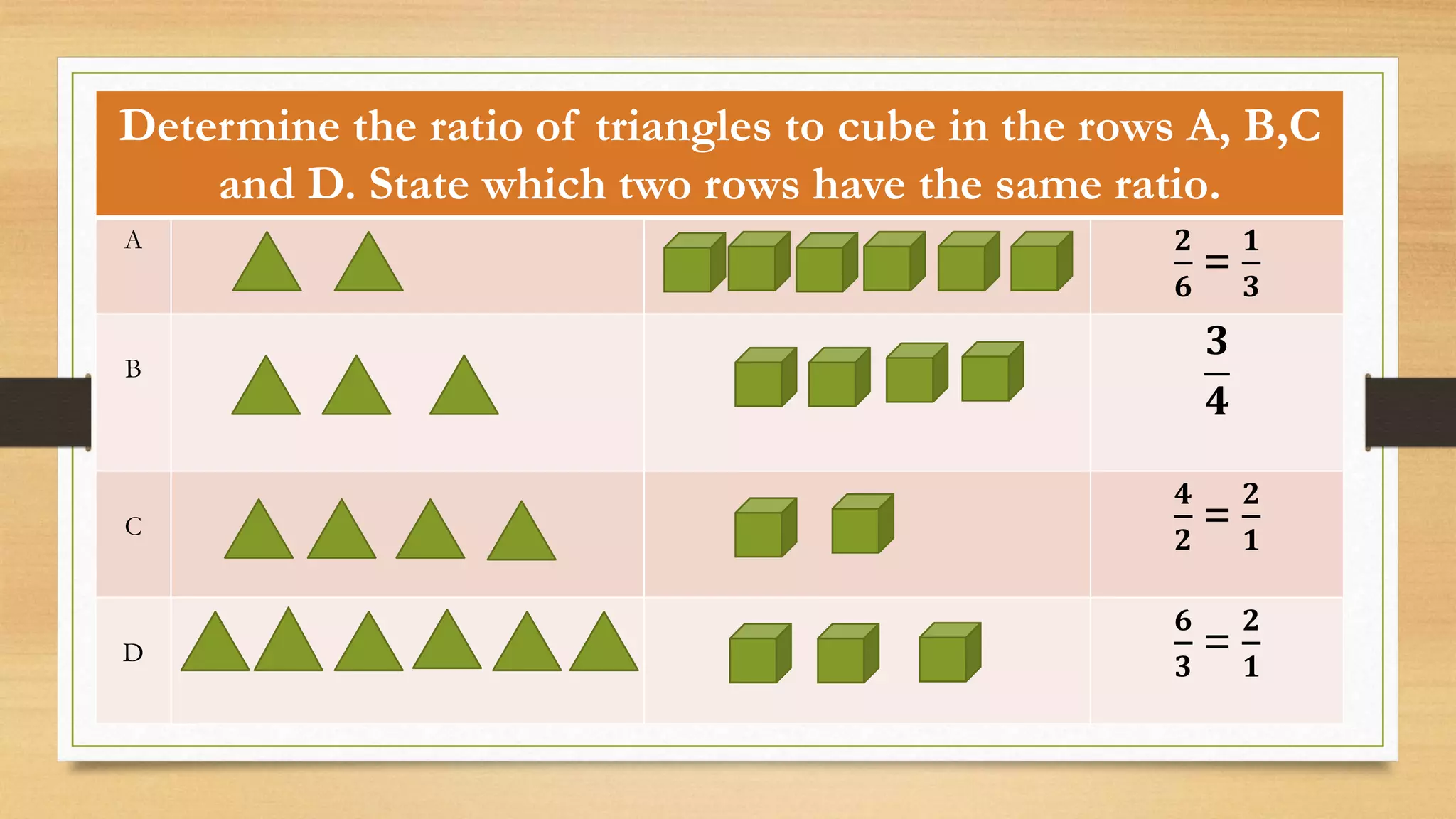
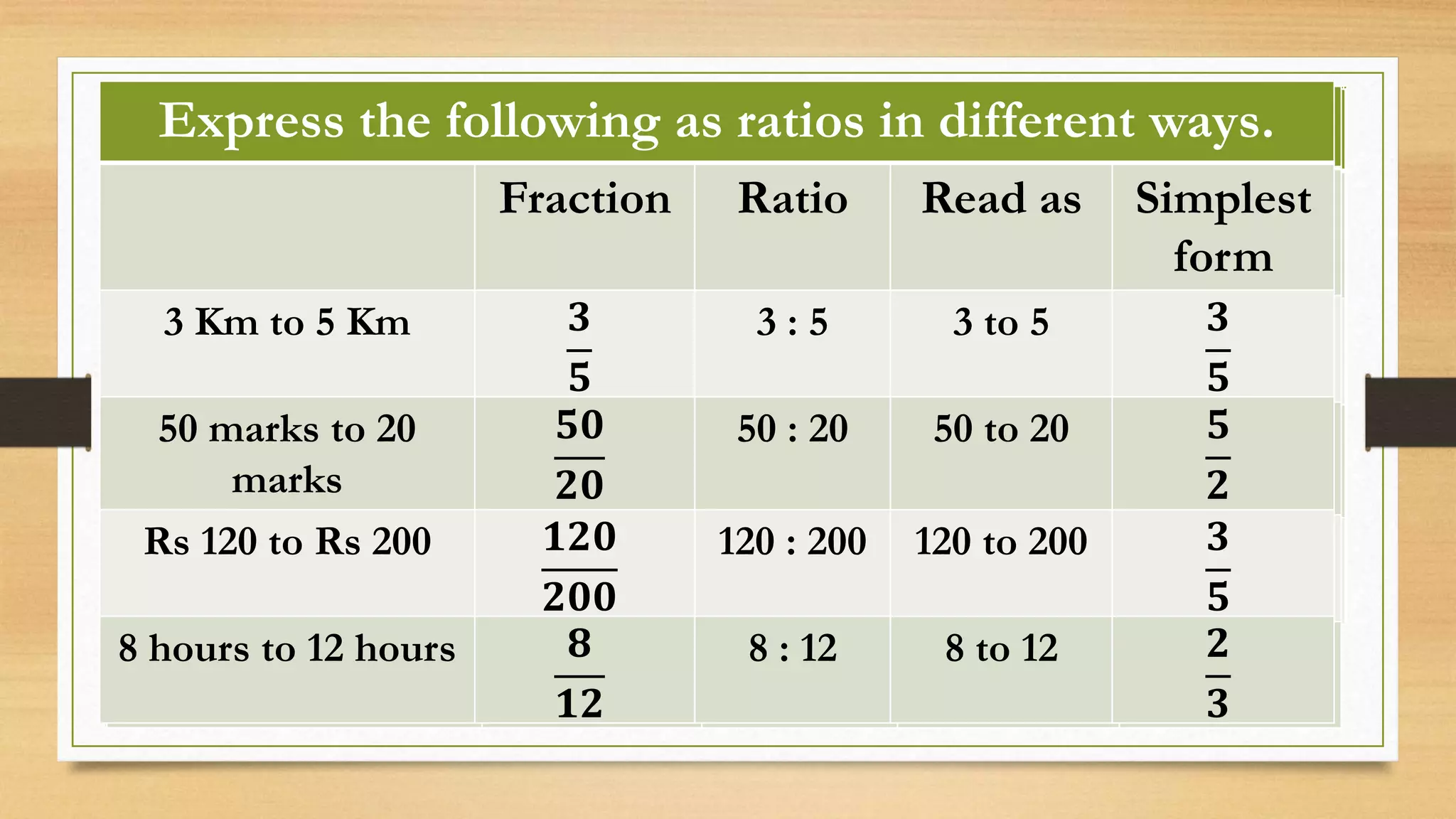
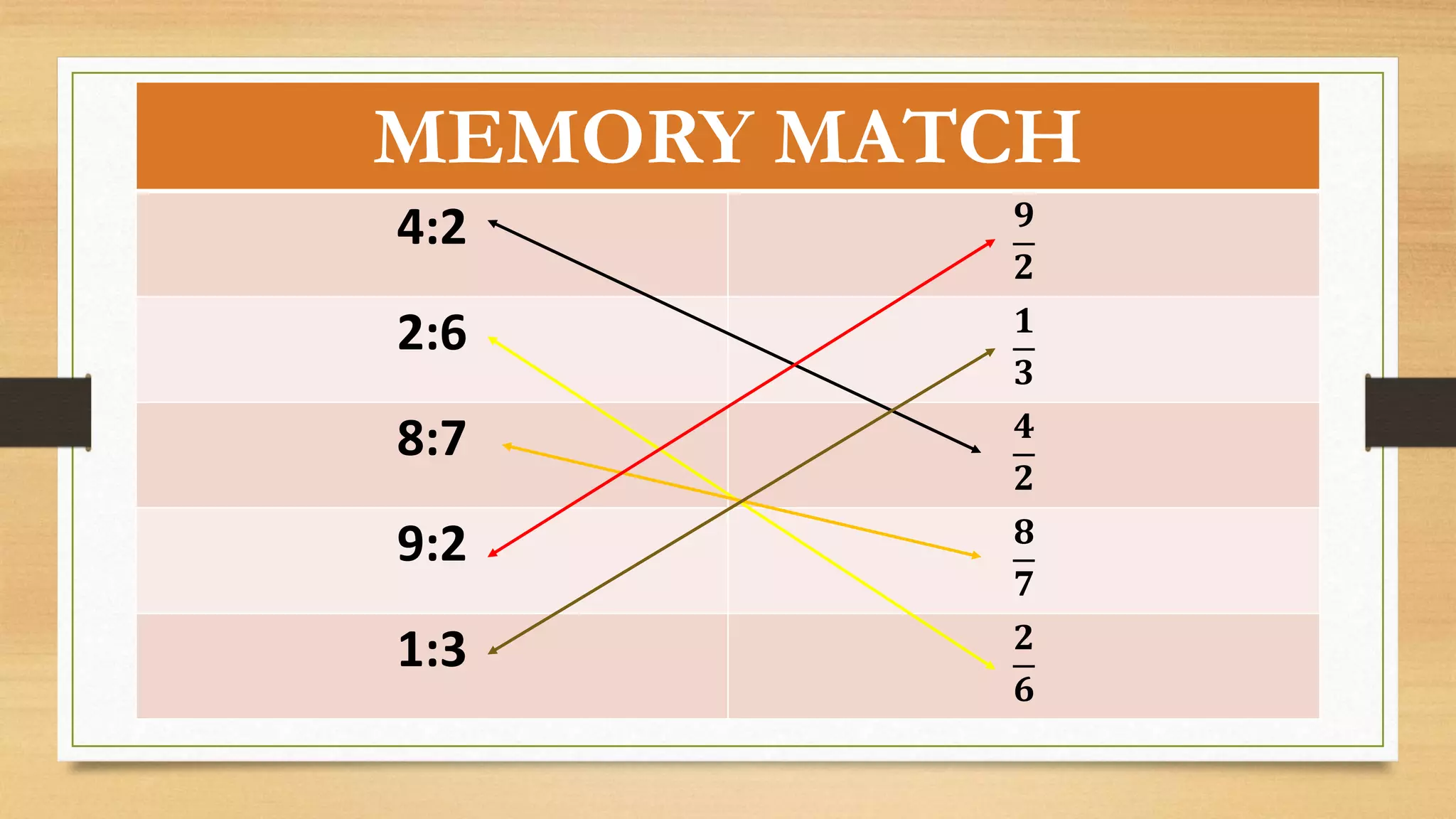
The document discusses the concept of ratios as a comparison of quantities, illustrating example calculations between two individuals collecting flowers and the relation of students in a class. It explains representation of ratios in various forms, including fractions, using the word 'to,' and colons, while providing multiple examples of simplifying ratios. The text also provides exercises for calculating ratios in different scenarios, reinforcing the concept through practical applications.
More Related Content
Similar to MATH - RATIO (CLASS V)
MATH - RATIO (CLASS V)
- 2.
- 3. Rita collected 21 flowers. Pamelacollected 42 flowers. Flowers collected by Pamela – Flowers collected by Rita 42 flowers – 21 flowers = 21 flowers This type of comparison is called comparison by difference.
- 4. Rita collected 21 flowers. Pamelacollected 42 flowers. 𝑭𝒍𝒐𝒘𝒆𝒓𝒆𝒔 𝒄𝒐𝒍𝒍𝒆𝒄𝒕𝒆𝒅 𝒃𝒚 𝑹𝒊𝒕𝒂 𝑭𝒍𝒐𝒘𝒆𝒓𝒆𝒔 𝒄𝒐𝒍𝒍𝒆𝒄𝒕𝒆𝒅 𝒃𝒚 𝑷𝒂𝒎𝒆𝒍𝒂 = 𝟐𝟏 𝟒𝟐 = 𝟏 𝟐 Rita has collected 𝟏 𝟐 the number of flowers of what pamela has collected.
- 5. Rita collected 21 flowers. Pamelacollected 42 flowers. 𝑭𝒍𝒐𝒘𝒆𝒓𝒆𝒔 𝒄𝒐𝒍𝒍𝒆𝒄𝒕𝒆𝒅 𝒃𝒚 𝑷𝒂𝒎𝒆𝒍𝒂 𝑭𝒍𝒐𝒘𝒆𝒓𝒆𝒔 𝒄𝒐𝒍𝒍𝒆𝒄𝒕𝒆𝒅 𝒃𝒚 𝑹𝒊𝒕𝒂 = 𝟒𝟐 𝟐𝟏 = 𝟐 𝟏 Pamela has collected twice the number of flowers that what Rita has collected.
- 6. Rita collected 21 flowers. Pamelacollected 42 flowers. 𝟐𝟏 𝟒𝟐 = 𝟏 𝟐 𝟒𝟐 𝟐𝟏 = 𝟐 𝟏 Rita has collected 𝟏 𝟐 the number of flowers of what pamela has collected. Pamela has collected twice the number of flowers that what Rita has collected. This is known as comparison by division.
- 7.
- 8. Comparison by divisionis called Ratio. RATIO In other word, Ratio is a Comparison of two or more quantities of the same kind by division.
- 9. Can the followingmeasures be compared with a ratio? 6 yellow fish in an aquarium with 18 fish Can the following measures be compared with a ratio? 6 yellow fish in an aquarium with 18 fish YES Sonia’s weight and the number of girls in her class Can the following measures be compared with a ratio? 6 yellow fish in an aquarium with 18 fish YES Sonia’s weight and the number of girls in her class NO Number of matchsticks in a matchbox and number of matchsticks in a carton full of matchboxes Can the following measures be compared with a ratio? 6 yellow fish in an aquarium with 18 fish YES Sonia’s weight and the number of girls in her class NO Number of matchsticks in a matchbox and number of matchsticks in a carton full of matchboxes YES The size of an ice cube in cm and the temperature inside the freezer in degree Celsius Can the following measures be compared with a ratio? 6 yellow fish in an aquarium with 18 fish YES Sonia’s weight and the number of girls in her class NO Number of matchsticks in a matchbox and number of matchsticks in a carton full of matchboxes YES The size of an ice cube in cm and the temperature inside the freezer in degree Celsius NO
- 10. Representation of aRatio. There are three ways of representing a Ratio. In fraction form Using colon (:) Using the word ‘to’
- 11. Representation of aRatio. In fraction form 𝟐𝟏 𝟒𝟐 = 𝟏 𝟐 𝟒𝟐 𝟐𝟏 = 𝟐 𝟏
- 12. Representation of aRatio. Using the word ‘to’ 𝟏 𝟐 = 1 to 2 𝟐 𝟏 = 2 to 1
- 13. Representation of aRatio. Using ‘colon’ 𝟏 𝟐 = 1 : 2 𝟐 𝟏 = 2 : 1
- 14. Do you know????? If‘a’ and ‘b’ are any two number, then a : b First term or Antecedent Second term or Consequent
- 15. Example • In afruit basket, there are 20 oranges and 10 pomegranates. Express it in the form of a ratio. Solution: In ratio of the number of oranges to the number of pomegranates is: Using colon (:) 20 : 10 Using the word ‘to’ 20 to 10 In fractional form 𝟐𝟎 𝟏𝟎
- 16. Ratio in simplestform If ‘a’ and ‘b’ are any two numbers, then ‘a : b’ is said to be its lowest form or simplest form, if a and b have no common factors except 1.
- 17. To express aratio in its simplest form a) Write the ratio as a fraction b) Divide the numerator and denominator by their HCF c) The answer is a fraction in its lowest form STEPS
- 18. Example Express the ratio24 : 9 in its simplest form Solution: Step 1 - Write the ratio as a fraction Ratio = 𝟐𝟒 𝟗 Step 3 - The answer is a fraction in its lowest form = 𝟖 𝟑 = 8 : 3 Step 2 - Divide the numerator and denominator by their HCF = 𝟐𝟒 / 𝟑 𝟗 / 𝟑 Hence, the ratio of 24 and 9 in its simplest form is 8 : 3
- 19. Express the followingratios in their simplest forms. 15 and 3 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 = 𝟓 𝟏 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 = 𝟓 𝟏 = 5 : 1 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 = 𝟓 𝟏 = 5 : 1 12 and 6 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 = 𝟓 𝟏 = 5 : 1 12 and 6 𝟏𝟐 𝟔 = 𝟏𝟐 ÷𝟔 𝟔 ÷𝟔 = 𝟐 𝟏 = 2 : 1 80 and 10 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 = 𝟓 𝟏 = 5 : 1 12 and 6 𝟏𝟐 𝟔 = 𝟏𝟐 ÷𝟔 𝟔 ÷𝟔 = 𝟐 𝟏 = 2 : 1 80 and 10 𝟖𝟎 𝟏𝟎 = 𝟖𝟎 ÷ 𝟏𝟎 𝟏𝟎 ÷𝟏𝟎 = 𝟖 𝟏 = 8 : 1 180 and 120 Express the following ratios in their simplest forms. 15 and 3 𝟏𝟓 𝟑 = 𝟏𝟓 ÷𝟑 𝟑 ÷𝟑 = 𝟓 𝟏 = 5 : 1 12 and 6 𝟏𝟐 𝟔 = 𝟏𝟐 ÷𝟔 𝟔 ÷𝟔 = 𝟐 𝟏 = 2 : 1 80 and 10 𝟖𝟎 𝟏𝟎 = 𝟖𝟎 ÷ 𝟏𝟎 𝟏𝟎 ÷𝟏𝟎 = 𝟖 𝟏 = 8 : 1 180 and 120 𝟏𝟖𝟎 𝟏𝟐𝟎 = 𝟏𝟖𝟎 ÷𝟔𝟎 𝟏𝟐𝟎 ÷𝟔𝟎 = 𝟑 𝟐 = 3 : 2
- 20. Brain storming In aclass, there are 20 boys and 40 girls. a) Find the ratio of the number of boys to the number of girls. b) Find the ratio of the number of boys to the total number of students. c) Find the ratio of the number of girls to the total number of students. d) Find the ratio of the number of students to the total number of girls.
- 21. Brain storming In aclass, there are 20 boys and 40 girls. a) Find the ratio of the number of boys to the number of girls. The ratio of the number of boys to the number of girls = 𝟐𝟎 𝟒𝟎 Solution : The number of boys = 20 The number of girls = 40 = 𝟐𝟎 𝟐𝟎 𝟒𝟎 𝟐𝟎 = 𝟏 𝟐 = 1 : 2
- 22. Brain storming In aclass, there are 20 boys and 40 girls. b) Find the ratio of the number of boys to the total number of students. The ratio of the number of boys to the number of students = 𝟐𝟎 𝟔𝟎 Solution : The number of boys = 20 Total number of students = 20 + 40 = 60 = 𝟐𝟎 𝟐𝟎 𝟔𝟎 𝟐𝟎 = 𝟏 𝟑 = 1 : 3 Therefore, the ratio of the number of boys to the number of girls is 1 : 3 in simplest form.
- 23. Brain storming In aclass, there are 20 boys and 40 girls. c) Find the ratio of the number of girls to the total number of students. The ratio of the total number of girls to the number of students = 𝟒𝟎 𝟔𝟎 Solution : The number of girls = 40 Total number of students = 20 + 40 = 60 = 𝟒𝟎 𝟐𝟎 𝟔𝟎 𝟐𝟎 = 𝟐 𝟑 = 2 : 3 Therefore, the ratio of the number of boys to the number of students is 2 : 3 in simplest form.
- 24. Brain storming In aclass, there are 20 boys and 40 girls. d) Find the ratio of the number of students to the total number of girls. The ratio of the total number of students to the number of girls = 𝟔𝟎 𝟒𝟎 Solution : The number of girls = 40 Total number of students = 20 + 40 = 60 = 𝟔𝟎 𝟐𝟎 𝟒𝟎 𝟐𝟎 = 𝟑 𝟐 = 3 : 2 Therefore, the ratio of the number of students to the number of girls is 3 : 2 in simplest form.
- 25. Determine the ratioof triangles to cube in the rows A, B,C and D. State which two rows have the same ratio. A B C D
- 26. Determine the ratioof triangles to cube in the rows A, B,C and D. State which two rows have the same ratio. A 𝟐 𝟔 = 𝟏 𝟑 B 𝟑 𝟒 C 𝟒 𝟐 = 𝟐 𝟏 D 𝟔 𝟑 = 𝟐 𝟏
- 27. Express the followingas ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 120 to 200 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 120 to 200 𝟑 𝟓 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 120 to 200 𝟑 𝟓 8 hours to 12 hours Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 120 to 200 𝟑 𝟓 8 hours to 12 hours 𝟖 𝟏𝟐 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 120 to 200 𝟑 𝟓 8 hours to 12 hours 𝟖 𝟏𝟐 8 : 12 8 to 12 Express the following as ratios in different ways. Fraction Ratio Read as Simplest form 3 Km to 5 Km 𝟑 𝟓 3 : 5 3 to 5 𝟑 𝟓 50 marks to 20 marks 𝟓𝟎 𝟐𝟎 50 : 20 50 to 20 𝟓 𝟐 Rs 120 to Rs 200 𝟏𝟐𝟎 𝟐𝟎𝟎 120 : 200 120 to 200 𝟑 𝟓 8 hours to 12 hours 𝟖 𝟏𝟐 8 : 12 8 to 12 𝟐 𝟑
- 28. RECAP • Ratio isa comparison of two or more quantities of the same kind by division. • There are three ways of representing a ratio. In fraction form Using the word ‘to’ Using colon ( : ) • If a and b are any two numbers, then a is said to be first term or antecedent and b is said to be second term or consequent.
- 29. MEMORY MATCH 4:2 𝟗 𝟐 2:6𝟏 𝟑 8:7 𝟒 𝟐 9:2 𝟖 𝟕 1:3 𝟐 𝟔
- 30. There are 36bananas,12 oranges and 24 apples in a basket. Write down the: a) Ratio of apples to oranges b) Ratio of bananas to oranges and apples c) Ratio of oranges to remaining