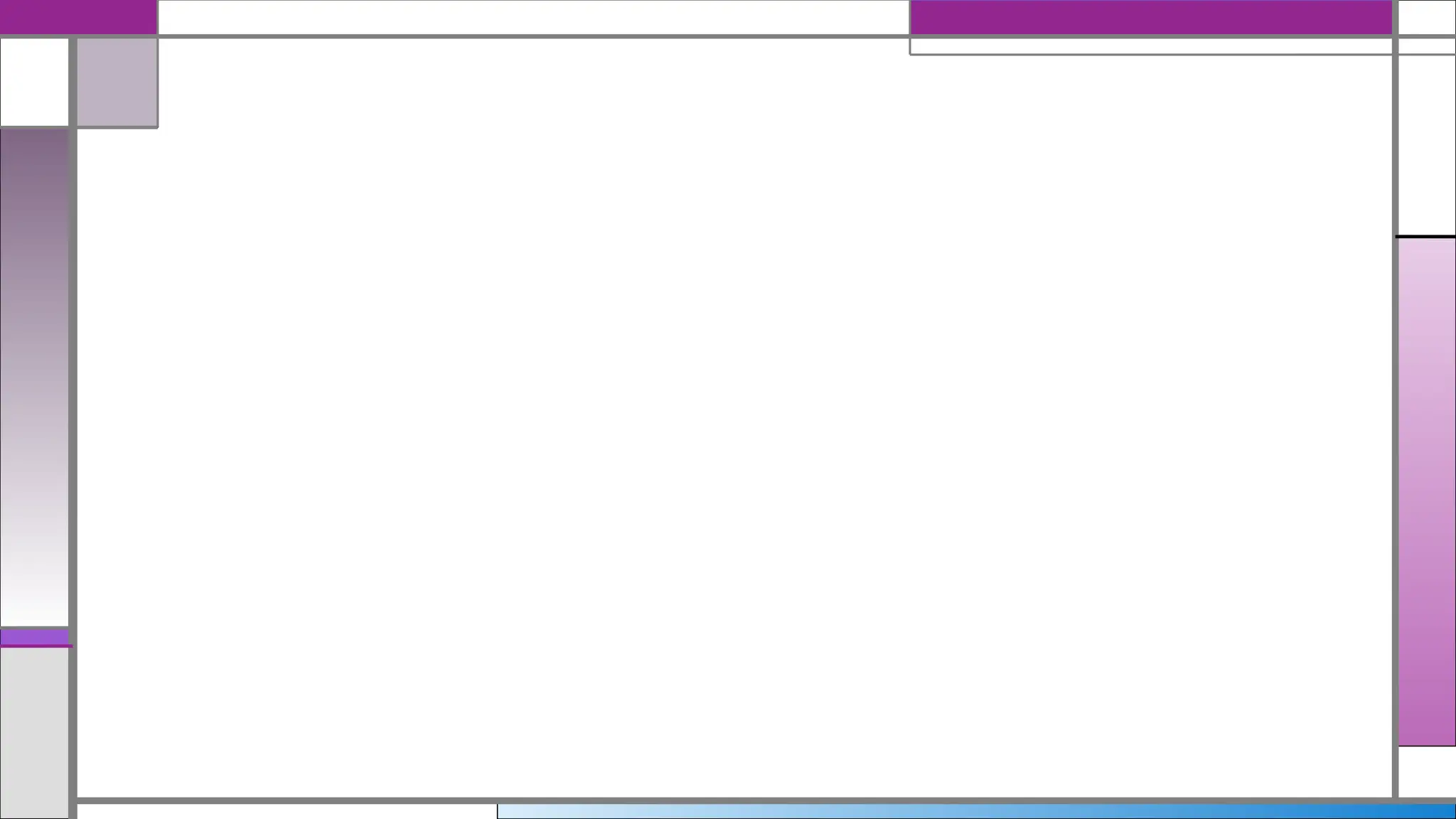
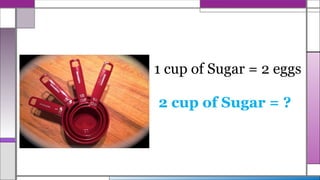
The document explains the concept of proportion, detailing its definition, types, and fundamental properties, particularly focusing on direct and indirect proportions. It provides various examples for real-life applications, illustrating how to solve proportion problems, such as reading speed, baking ratios, and working hours. Additionally, it includes practice activities and explanation of scenario-based problems involving ratios and proportions.

2. The ratio 5 to 6 equals the ratio 10 to 12” or as “5 is
to 6 as 10 is to 12.”
12
10
6
5
 5:6=10:12

3. Some situations/examples are the following:
• A. Mark reads 10 pages of a manuscript in 15 minutes. At
this rate, how many pages will he read in 25 minutes?
• B. When baking, 3 cups of flour require 5 eggs. If you make
cookies requiring 5 cups of flour, how many eggs will you
need?
• C. Marty is paid PhP880 per two hours of lecture. In a
week, he lectures for 9 hours. How much would he be paid?

4. PROPORTION

5. What is PROPORTION?
• A statement that two ratios are
equal is called proportion.
• Comparison of two ratios.
• If and are two equal ratios,
then the statement = is called a
proportion.

6. Parts of proportion
=
a is the first term;
b the second term;
c the third term; and
d the fourth term.
The first and fourth terms (a&d) are called the extremes.
The second and third terms (b&c) are called the means.

7. Parts of proportion
=

9. FUNDAMENTAL
PROPERTY OF
PROPORTION

10. 1. In any proportion, the product
of the means is equal to the
product of the extremes.
• if , then a:d = b:c
d
c
b
a

Means
Exremes
FUNDAMENTAL PROPERTY OF
PROPORTION

11. 12
10
6
5

X
60
60

12. Example:
1. 3. 5.
2. 4. 6.
16
14
8
7

22
18
10
8

12
9
4
3

5
7
7
5

6
2
12
4

9
8
8
5

PROPORTION PROPORTION PROPORTION
NOT PROPORTION NOT PROPORTION
NOT PROPORTION
X
112
112

13. Find the missing term
1. 2.
Solution:
7:8 = n:16 n:6 = 10:3
8n = 112 3n = 60
n =14 n = 20
16
8
7 n

3
10
6

n

14. Find the missing term
3. 5.
4. 6.
3
14
7

x n
n 6
6

60
:
15
:
4
1
x

3
2
5
4 

 n
n

15. Solution
3. 7:x=14:3 5. n:6=6:n
14x=21 36=
x=1.5 n
n=6
4. 6. (n+4):5=(n-2):3
15x=15
x=1
60
:
15
:
4
1
x

5(n-2)=3(n+4)
5n-10=3n+12
5n-3n=12+10
2n=24
n=12

16. Find the missing term
1. 120:0.48=300:x
2. x:0.75=19.2:36
3. 0.25:1.5=x:3

17. Example 1
•Eight tea bags are needed to make 5
liters of iced tea. How many tea bags
are needed to make 15 liters of iced
tea

18. Solution:
=
5 (t) = 15(8)
t = 24 tea bags

19. Example 2
A manufacturer knows that during an
average production run, out of 1,000
items produced by a certain machine, 25
will be defective. If the machine produces
2,030 items, how many can be expected
to be defective?

20. Solution:
•We let x represent the number of defective items
and solve the following proportion:
=
1000x=25(2030)
1000x=50750
x=50.75

21. Example 3
If 1 out of 6 people buy a
particular branded item, how
many people can be expected to
buy this item in a community of
6,000 people?

22. Solution
• Let p = the number of people buying the branded
item.
=
6000=6p
p=1000
• So, 1000 people can be expected to buy the particular
branded item.

23. TYPES OF
PROPORTION

24. AGE HEIGHT

26. 1 cup of Sugar = 2 eggs
2 cup of Sugar = ?

27. 1L of gasoline=2 kilometers
2L of gasoline= ?

28. 1. Direct Proportion
•two variables, say x and y, varying such
that as x increases y also increases or as
x decreases, y also decreases
proportionally; that is, the ratio is
always same. The same holds true with
the ratio .

29. Direct Proportion
“an increase in one quantity results to
an increase in another quantity and a
decrease in one quantity results to a
decrease in another quantity.”
y = kx

30. SPEED AND TRAVEL TIME

31. •Price and number of items purchased
•Number of People and the Time that is taken to
complete a Particular Task Number of Vehicles
on the Road and Free Space on Road
•Number of Vehicles on the Road and Free
Space on Road
•Time and Freshness of a Food Item

32. Indirect/Inverse
•two variables, say x and y, varying
such that as x increases, y
decreases, or as x decreases, y
increases proportionally; that is,
the product of x and y is always the
same.

33. Inverse Proportion
“an increase in one quantity
results to an decrease in another
quantity.”
x
k
y 

34. Partitive Proportion
•a whole is divided into more than
two parts.

35. APPLICATION
PROBLEM

36. Example 4
Two boxes of chocolates cost
PhP180. How much do 7 boxes
of chocolates cost?

37. Solution:
• The more the boxes, the higher the cost; that is, both
quantities are increasing. We have a direct
proportion.
• The ratio is always the same.
• That is,=

38. Example 5
•Forty liters of water is
transferred into 3 containers in
the ratio 1:3:4. How much
water is in each container?

39. Solution
•The ratio 1:3:4 indicates 1 + 3 + 4 = 8 portions.
•40 liters will be divided into 8 portions; that is,
= 5 liters (L) per portion
•Container 1 (1 portion) = 1 x 5 L = 5 L
• Container 2 (3 portions) = 3 x 5 L = 15 L
• Container 3 (4 portions) = 4 x 5 L = 20 L

40. Example 6
•If Trina works 20 hours, she
earns PhP600. How much
does she earn if she works
30 hours?

41. Solution
• This is a direct proportion problem; that is, the more
hours Trina works, the more she earns.
• Let x represent Trina’s earnings for working 30 hours.

42. Example 7.
•If nine men take 15 days to
assemble 18 machines, how
many days will it take 20
men to assemble 60
machines?

43. Solution
• This problem is a combination of direct and indirect
relations.
22.5 days

44. Activity
1. Jessa buys three bananas for PHP25.00. How much does she have to pay for a dozen
of these bananas?
2. A typist can finish 4 pages in 6 minutes. How long will it take him to finish 18 pages?
3. A menu which serves 5 people requires 3 cups of flour. How many cups of flour are
needed for the menu to serve 20 people?
4. To finish a certain job in 8 days, 6 workers are needed. If it is required to finish the
same job in 2 days advance, how many workers have to work?
5. A supply of food lasts for a week for 20 families. How long would the supply last if 3
more families have to be supplied?
6. A deceased person stated in his testament that his 30-hectare land be divided among
his three children using 1:2:3 partition, the oldest getting the biggest share. How
much did the second child receive?
7. The ratio of cups of water to cups of sugar in a menu is 3:1: .if this is just for one
serving, how much of each is needed for a menu that makes 5 servings?

46. More Example

47. Direct Proportion
1. For every 1 kilo of flour, 50 pieces of pastel can be
made. How many kilos of flour are needed to produce
575 pieces of Pastel?

48. Direct Proportion
2. Nina earns 10, 000 in 20 days for her online
business. How much will she earn at 30 days?

49. Inverse Proportion
1. If two workers can finish packing products in four weeks.
How many workers are needed if the target schedule should
only be three weeks?

50. Inverse Proportion
2. If 6 men can paint the wall in 64 hours, find the number of
men required to paint the wall in 48 hours?

51. Partitive Proportion
1. Jessa, Abel, and Edward are partners in the Beauty shop
business. They agreed to divide their profits in a ratio 1:2:3.
How much should each receive if the total profit is 50, 000.00?

52. 6. If 6 men take 13 days
to assemble 16 furniture,
how many days will it
take 18 men to assemble
58 furniture?

53. Solution
• This problem is a combination of direct and indirect
relations.